Psicothema was founded in Asturias (northern Spain) in 1989, and is published jointly by the Psychology Faculty of the University of Oviedo and the Psychological Association of the Principality of Asturias (Colegio Oficial de Psicología del Principado de Asturias).
We currently publish four issues per year, which accounts for some 100 articles annually. We admit work from both the basic and applied research fields, and from all areas of Psychology, all manuscripts being anonymously reviewed prior to publication.
Psicothema, 2004. Vol. Vol. 16 (nº 1). 163-169
Paula Fernández, Guillermo Vallejo y Javier Herrero
Universidad de Oviedo
La precisión de nueve procedimientos para el cálculo de la autocorrelación ha sido evaluada en un diseño de Grupos x Ocasiones. Utilizamos seis estucturas de matrices de dispersión (Σ) con ausencia de autocorrelación serial: Simetría Combinada, Huynh-Feldt, No Estructurada (ε= .56 y ε= .75) y de Coeficientes Aleatorios (ε= .56 y ε= .75). Los resultados indican que el procedimiento de Hearne, Clark y Hatch (1983) realiza una estimación ajustada independientemente del tamaño de la muestra y del número de puntos de serie salvo cuando la matriz subyacente es de Simetría Combinada o Huynh-Feldt. El resto de los estimadores dependen de q y de Σ y sólo los procedimientos de Jones (1985) y de Pantula y Pollock (1985) dependen significativamente del tamaño de la muestra. Los procedimientos de Wilson, Hebel y Sherwin (1981), Gill (1992) y Pantula y Pollock (1985), en este orden, son los más afectados por el maridaje ausencia de autocorrelación-ausencia de esfericidad.
Serial autocorrelation equal to zero. Precision for the estimation. The precision of nine procedures for the calculation of the autocorrelation was evaluated in a Groups x Occasions design. Whe have used six different structures of dispersion matrices (Σ) that have absence of serial autocorrelation. These were: Compound Symmetric, Huynh-Feldt, Unstructured (ε= .56 y ε= .75) and of Random Coefficients (ε= .56 y ε= .75). The results show that the Hearne, Clark & Hatch (1983) procedure reaches a right estimation independently of the sample size and of the number of series points (q) except when Σ is of Compound Symmetric or Huynh-Feldt. The rest of the procedures depend on q and on Σ, and only the Jones (1985) and Pantula & Pollock (1985) procedures depend significantly on sample size. The procedures of Wilson, Hebel & Sherwin (1981), Gill (1992) and Pantula & Pollock (1985), in this order, are the most affected by the marriage absence of autocorrelation-absence of sphericity.
Una de las estructuras que con más frecuencia adoptan los diseños de medidas repetidas es aquella que contiene un único factor A entre-sujetos (grupos) que representa una variable, bien de tratamiento bien de clasificación, con j=1,...,p niveles que contienen p muestras aleatorias de nj unidades experimentales. Cada una de estas unidades experimentales es observada en un reducido número de ocasiones k=1,...q (factor B intra-sujeto) resultantes de una elección sistemática de intervalos de tiempo fijos y equidistantes. Este procedimiento de recogida de datos que denominamos diseño de Grupos x Ocasiones (Fernández, Vallejo y Escudero, 2002) es susceptible de manifestar el efecto secuencial de dependencia serial. Por este motivo, y en función de la estrategia analítica que se utilice para poner a prueba las hipótesis estadísticas, es posible que la validez de conclusión estadística resulte comprometida.
Asumiendo la existencia de normalidad y homogeneidad de las matrices de dispersión, las hipótesis correspondientes a los efectos de este diseño se pueden contrastar utilizando una aproximación multivariada y/o univariada. El modelo multivariado de la varianza (AMVAR) no impone ninguna estructura a la matriz de varianza-covarianza (Σ), excepto que sea definida positiva. Por este motivo, todos los parámetros de la matriz deben ser estimados (con q medidas repetidas son q(q+1)/2), sin embargo, si hay más medidas repetidas que grados de libertad residuales, la matriz será singular y el AMVAR no podrá ser calculado. La bondad del modelo mixto univariado de la varianza descansa en la estructura de la matriz Σ que, en su forma menos restrictiva, requiere la condición de esfericidad multimuestral. Si esta asunción no se cumple, podemos utilizar alguna de las estrategias que existen para calcular la desviación de la matriz de covarianza muestral del patrón requerido y proceder en consecuencia. Sin embargo, ninguna de ellas asume que la correlación entre las observaciones en distintos puntos del tiempo es una función de la distancia temporal entre ellos. Como la autocorrelación serial (ρ) entre las puntuaciones es condición suficiente para que la matriz Σ no se acomode al patrón de esfericidad requerido algunos autores (Anderson, 1971; Andersen, Jensen y Schou, 1981; Azzalini, 1984; Hearne, Clark y Hatch, 1983; Pantula y Pollock, 1985; Schmitz, 1990; Jones, 1985) han propuesto modelos univariados de la varianza que tienen en cuenta la dependencia serial. No obstante, la bondad de estas últimas estrategias está determinada por la estimación previa y fiable de la autocorrelación.
Recientemente, Fernández et al., (2002) han evaluado comparativamente mediante simulación Monte Carlo la precisión de nueve estimadores diferentes del parámetro autorregresivo de primer orden en diseños de medidas repetidas. Sus resultados pusieron de relieve que los procedimientos que mejor estiman el valor del parámetro, tanto para procesos con autorregresión positiva como negativa, son: ρHCH (Hearne et al., 1983), ρJ (Jones, 1985), ρPP (Pantula y Pollock, 1985) y ρWHS (Wilson, Hebel y Sherwin, 1981). En concreto, los procedimientos ρHCH y ρWHS estiman correctamente el valor del parámetro autorregresivo con independencia del valor que toman q, nj y ρ. El procedimiento ρPP también estima correctamente el valor del parámetro con independencia de ρ, pero mejora sensiblemente conforme q y nj incrementan. Por su parte, el estimador ρJ depende tanto de ρ (mejor estimación cuanto menor es el valor de la autocorrelación |ρ|), como de nj y de q, que, si éstos incrementan, mejora notablemente la estimación para valores elevados del parámetro. Cuando la matriz de desviación es no estacionaria decreciente ningún procedimiento resulta afectado. Si es no estacionaria creciente sólo resultan afectados ρPP, ρWHS y ρG (Gill, 1992), aunque de modo significativo sólo el primero. Estos autores concluyeron que cuando la matriz subyacente tiene estructuras AR(1) o ARH(1), por lo general, los procedimiento cuya estimación es robusta o cercana a la robustez y experimentan alguna variación en función de la intensidad de |ρ|, realizan mejor estimación cuanto más pequeña es ésta y mayor es q. Sólo cuando son pocos los niveles de la variable intra y |ρ| es elevada, el tamaño de la muestra es un factor determinante.
¿Cómo se comportan estos estimadores cuando no existe dependencia serial? ¿Estiman que la autocorrelación es cero –o sólo se aproximan– cuando no existe autocorrelación serial de primer orden? La ausencia de autocorrelación puede estar o no acompañada de esfericidad, ¿la estimación se modifica en función de la desviación de esta asunción? El comportamiento de los procedimientos cuya estimación era más ajustada cuanto menor era el valor del parámetro, ¿es mejor ahora? Todas estas cuestiones no fueron abordadas por Fernández et al., (2002) y aún permanecen abiertas.
Método
Breve definición de los estimadores
Estimadores máximo verosímiles:
– ρHCH: Hearne y otros, (1983), basándose en el trabajo de Koopmans (1942) derivaron la siguiente expresión para el cálculo MLE de ρ.
(1-1/q)A2ρ3 - (1-2/q)A1ρ2 - {(1+1/q)A2+A3/q}ρ + A1= 0 (1)
ρ es la raíz real más cercana a A1/(A2+A3) que resulta de resolver (1). Siendo A1, A2 y A3
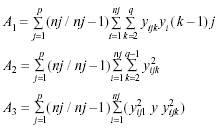
– ρJ: Jones (1985) propone para la estimación MLE el valor de ρ(-0.99≤ρ < 0.99) que minimiza la expresión L(ρ)= -2 ln (verosimilitud). La fórmula para L(ρ) depende del tamaño relativo entre las sumas de cuadrados del error entre sujetos (SCE) e intra sujetos (SCI) calculados corrigiendo el valor de la autocorrelación como sigue:
Si (q-1) SCE ≥ SCI, entonces L(ρ)=N[(q-1)ln (SCI/N(q-1))+ln(SCE/N)- ln(1-ρ2)]
Si (q-1) SCE < SCI, entonces L(ρ)=N[qln ((SCE+SCI)/Nq)-ln(1-ρ2)]
Estimadores de momentos:
– ρAJS: Desarrollado por Bartlett (1956) y expuesto por Andersen y otros (1981).
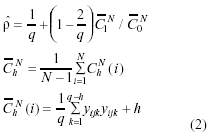
– ρABD: Azzalini y Browman (1990) realizan una extensión del estimador que Daniels (1956) propuso para n>1.
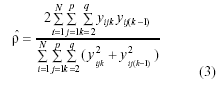
– ρAB: Azzalini y Browman (1990) proveen una corrección para la estimación anterior
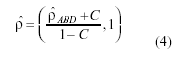
donde C= (q-1)-1
– ρPP: Pantula y Pollock (1985)
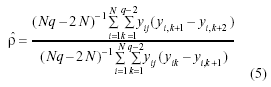
– ρrG: Gill (1992)
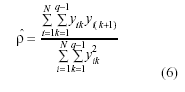
Para estimar ρ, los procedimientos ρHCH, ρJ y ρPP utilizan el error entre sujetos y, ρAJS, ρABD, ρAB, y ρG el error intra sujetos, indicado por yijk indistintamente.
– ρWHS: Wilson, Hebel y Sherwin, (1981) desarrollan una estimación para el cálculo de la autocorrelación de orden uno que denominan subóptima, donde,
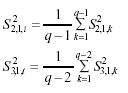
son respectivamente, el promedio de todas las posibles varianzas que pueden ser calculadas desde dos observaciones adyacentes, y el promedio de todas las posibles varianzas que pueden ser calculadas desde tres observaciones contiguas espaciadas dos unidades de tiempo dentro de un individuo. El promedio para el conjunto de individuos es S22,1,. ,. y S23,1,. ,. Entonces:
![]()
– ρAFD: Azzalini y Frigo (1991) ofrecen también una extensión del procedimiento de Daniels (1956) para n>1 utilizando las puntuaciones directas (xijk) en lugar de los residuales (yijk).
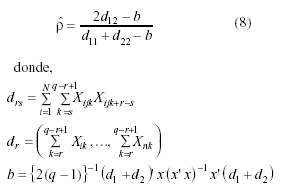
siendo X la matriz de identidad de orden N
Con la intención de examinar lo expresado anteriormente en la introducción, realizamos un estudio Monte Carlo con datos generados desde distribuciones normales multivariadas. Cuatro variables fueron manipuladas: (a) tamaños de las muestras (nj), (b) ocasiones de medida (q), (c) estructura de la matriz de covarianza de la población (Σ), y (d) grado de heterogeneidad entre las matrices de covarianza (GHE). Los resultados se refieren a un diseño balanceado de Grupos x Ocasiones y se exponen articulados de acuerdo a la ausencia de autocorrelación serial (NR) para las [q, nj(N), GHE, NR]=[4x3x4x6]=288 condiciones experimentales que resultan de manipular las variables indicadas entre corchetes. A saber, q=4, 6, 8 y 12 niveles del factor intra-sujeto (ocasiones de medida); nj = 5, 10 y 16 son los tamaños de los vectores de observaciones en cada uno de los 3 grupos, por lo tanto, los tamaños de muestra totales (N) son 15, 30 y 48 respectivamente.
Seis son las estructuras de matrices de dispersión con ausencia de autocorrelación serial que hemos utilizado, a saber: Simetría Combinada (SC) , Huynh-Feldt (HF), Coeficientes Aleatorios (CA) (ε =.56 y ε =.75) y No estructurada (NE) (ε = .56 y ε = .75). La matriz de SC disfruta de varianzas y covarianzas constantes. En concreto ha sido construida desde la expresión Eqq = A + A’ + l Ik donde A es una matriz (qxq) con todos sus elementos iguales, I es la matriz identidad y λ es una constante arbitraria, que en un caso particular depende de la relación entre los tratamientos, la escala de medida, así como de las varianzas y covarianzas. En nuestro caso λ=10. La matriz HF es más general que la matriz SC. Satisface la propiedad σ2kk + σ2k'k' - σkk' = 2λ. Tiene un diseño generado de la misma forma que SC salvo que Aqq es ahora una matriz de columnas iguales donde cada uno de los elementos son ordinalmente diferentes. La matriz NE es una matriz simétrica donde las varianzas como las covarianzas varían sin ninguna estructura definida. CA fué construida desde la expresión Eqq= Z Φ Z’ + σ2I (Jennrich y Schluchter, 1986) donde Z es una matriz conocida qxr siendo unos la primera columna. Φ es una matriz de dispersión rxr que en nuestro caso fue no estructurada (Laird y Ware, 1982).
La estructura de la matriz de SC es homogénea porque las varianzas y covarianzas son constantes. Por otra parte, las matrices HF, CA y NE exhiben heterogeneidad intrasujeto (Litlell, Milliken, Stroup y Wolfinger, 1996; Wolfinger, 1996) y por tanto las varianzas varían para cada observación (q) aunque no de igual forma. En la matriz HF las varianzas y covarianzas crecen proporcionalmente, mientras que en las matrices CA y NE las varianzas y covarianzas varían sin ninguna estructura definida.
Todas estas matrices manifiestan ausencia de autocorrelación serial, pero en modo diferente. En la matriz SC la correlación es constante, es decir, las variables aleatorias del modelo están igualmente correlacionadas para todos los pares de observaciones de cada sujeto. La matriz HF tiene una estructura especial de correlación. La correlación entre dos puntos igualmente distantes es moderadamente creciente (disminuyendo en intensidad) a medida que el par está más lejos en la serie. Por otra parte, la correlación entre dos ocasiones de observación se incrementa proporcionalmente conforme éstas se alejan en el tiempo. En ambas, SC y HF, se satisface la asunción de esfericidad y por lo tanto ε= 1. En las matrices CA y NE la correlación entre las diferentes medidas (q) es arbitraria y por este motivo carecen de esfericidad. En la construcción de estas últimas utilizamos el algoritmo desarrollado por Cornell, Young y Bratcher (1991) para que presenten desviación de la esfericidad moderada (ε= 0.75) y grave (ε= 0.56).
Con cada una de las estructuras precedentes utilizamos iguales y diferentes matrices de dispersión para el factor entre sujetos (GHE) que proveen situaciones desde la homogeneidad ortodoxa hasta una elevada violación de esta asunción. Las razones construídas fueron: (1:1:1), (1:1.5:2), (1:2:3) y (1:3:5).
A continuación, vectores Zij de variadas normales [N ~ (N, σ2) = N ~ (0,1)] fueron generados mediante el algoritmo de Kinderman y Ramage (1976) implementado en el programa GAUSS (Aptech Systems, 1997, V. 3.2.32). Los vectores de observaciones pseudoaleatorios y’ij1,...,y’ijq con matriz de varianzas-covarianzas Σ fueron obtenidos a través del método de Schauer and Stoller (1966), esto es Y’ij = T Zij , donde T es la factorización de Cholesky de Σj.
El programa de simulación fue escrito en el lenguaje de programación GAUSS (1997). 10.000 replicaciones de cada condición fueron ejecutadas para cada uno de los nueve procedimientos.
Resultados
Las pruebas de significación que descansan en la independencia de las observaciones son sensibles a pequeñas desviaciones de la ausencia de autocorrelación serial. Por esta razón, se presupone que el contraste de las hipótesis resulte perjudicado cuando se estiman pequeñas autocorrelaciones que no existen, y se utilice en consecuencia, alguna estrategia que pretende su corrección. En virtud de ello, el criterio de robustez que consideramos para evaluar las condiciones particulares bajo las cuales los diferentes procedimientos de cálculo son insensibles a la estructura subyacente de no autocorrelación serial de primer orden, a la razón nj/q y a la violación de la asunción de homogeneidad de las matrices de covarianza entre grupos, es que el sesgo empírico (SE) no exceda de .07.
SE= (ρ ^ - ρ) ≤ .07
Consideramos que un procedimiento es ajustado si la estimación empírica (EE) está contenida en el intervalo ρ±.02. A pesar de que no existe una regla universal para este cometido esta medida cuantitativa ha sido considerada en el ámbito de las series temporales cortas (ver Arnau, 1999), y en nuestra opinión, constituye un criterio adecuado para juzgar la robustez.
En las tablas que siguen presentamos los resultados para un subconjunto seleccionado de combinaciones investigadas que muestran adecuadamente las diferencias que existen entre los procedimientos con respecto a la estimación empírica de ρ. ρG, ρABD y ρAFD manifestaron un comportamiento muy similar en su EE, con diferencias entre ellos inferiores a .02, razón por la que decidimos exponer sólo la estimación para el procedimiento ρG. Tampoco presentamos los resultados en condición de heterogeneidad entre grupos porque ningún procedimiento resultó afectado por esta razón en ninguna de las condiciones estudiadas. Esto es esperable si tenemos en cuenta que las matrices son proporcionales, y por ende, tienen la misma estructura.
EEρ para matrices de dispersión con estructuras de SC y de HF. ε= 1 (Tabla 1)
El procedimiento ρHCH manifiesta una estimación liberal en la misma cuantía para cualquier razón nj/q si la matriz subyacente a los datos es de SC. Cuando la matriz tiene estructura HF la estimación es liberalmente creciente en función de q, pero invariable con respecto a nj.
ρJ experimenta una estimación liberal si la matriz de dispersión es de SC cuando q < 6 y nj ≤ 10, de otro modo el comportamiento es robusto y ajustado. Cuando la matriz subyacente es de Tipo HF la estimación sólo es liberal para q= 4 independientemente de nj. En otras situaciones el procedimiento se comporta de modo robusto y ajustado.
ρAJS exhibe robustez siempre que q≥6 y se ajusta cuando q≥8 independientemente del tamaño de la muestra.
ρG, ρABD y ρAFD se muestran robustos y ajustados para q= 12, de otro modo son muy conservadores, en mayor medida cuanto menor es q. No dependen de nj.
ρAB, ρPP y ρWHS estiman de modo robusto y ajustado para cualquier razón nj/q.
EEρ para matrices de dispersión con estructura NE ( ε= .75 y ε= .56) (Tabla 2)
Cuando ε = .75 y q= 4 todos los procedimientos, sobre todo ρAB, ρPP y ρWHS, y con independencia del tamaño de muestra, están lejos de alcanzar la robustez. Si q≥6 los procedimientos ρHCH, ρJ, ρAJS y ρrAB manifiestan un comportamiento ajustado y ρWHS robusto para toda razón nj/q.
ρAB es robusto para la razón nj/q= 5/6 y ajustado de otro modo.
ρG, ρABD y ρAFD exhiben un comportamiento conservador para q≤6 y nj≤10, robusto para q= 8 y ajustado si q= 12.
Cuando ε=.56 el comportamiento anterior se agrava levemente si q= 4 para todos los procedimientos. Cuando la razón nj /q es 5/6, ρAJS y ρPP resultaron levemente más liberales aunque no abandonan la robustez. El comportamiento de ρG, ρABD y ρAFD también es levemente más liberal aunque no de modo significativo con respecto a ε = .75. El procedimiento ρWHS es el más afectado al incrementarse la desviación de la esfericidad, manifestándose conservador para todo q y nj.
EEρ para matrices de dispersión con estructura de CA ( ε= .75 y ε= .56) (Tabla 3)
Cuando ε =.75 los procedimientos ρHCH y ρAB tienen un comportamiento robusto y ajustado para toda razón nj/q que no se modifica cuando la desviación de la esfericidad es mayor. ρJ, ρAJS y ρPP, en este orden de mejor a peor, manifiestan un comportamiento similar, y al menos robusto, para toda razón nj/q. rJ se ajusta siempre para q≥6 y para la razón nj/q= 16/4. La estimación de ρAJS y ρPP es ajustada siempre que q≥8 y el primero también para la razón nj/q= 10/6. Cuando ε= .56 estas estimaciones se tornan conservadoras y pierden la robustez como sigue: ρJ para la razón nj/q= 5/4, ρAJS para las razones 5/4 y 10/4 y ρPP siempre para q≤6.
ρG, ρABD y ρAFD realizan una estimación ajustada para q= 12, conservadora de otro modo, en mayor medida cuanto menor es. Este comportamiento se agrava para ε=.56 aunque sin modificar significativamente los resultados anteriores.
ρWHS es robusto sólo si q= 12 y ε=.75; cuando ε=.56 pierde la robustez. Para otros niveles de q es conservador, en mayor medida cuanto menor es q, aunque menos que ρG, ρABD y ρAFD. Estos cuatro últimos estimadores son insensibles al tamaño de la muestra.
Discusión y conclusiones
El procedimiento MLEρHCH que realizaba una estimación ajustada independientemente de ρ, nj y q cuando la matriz de dispersión subyacente a los datos era AR(1) y ARH(1) (Fernández et al., 2002) conserva esta virtud cuando la matriz de dispersión que subyace a los datos es NE (si q>4) y de CA, pero no si es de tipo SC o H-F. La estimación empírica que realiza bajo estas dos condiciones coinciden con la media de las correlaciones entre todos los puntos distanciados una unidad de tiempo. Cuando la matriz subyacente es del tipo SC toma el mismo valor con independencia de q dado que la correlación es constante entre cualquier par de observaciones, mientras que se incrementa en función de q cuando la matriz es del tipo HF.
Con respecto al procedimiento MLE ρJ, los autores anteriormente citados concluyeron que era un procedimiento ligado al valor del parámetro. En concreto, cuanto menor era la intensidad de la autocorrelación serial, independientemente de si la dirección era positiva o negativa, mejor era la estimación. El comportamiento eficiente para elevados valores del parámetro dependía tanto de q como del tamaño de muestra. Así las cosas, esperábamos que rJ mostrase un comportamiento ajustado en condiciones de ausencia de autocorrelación, sin embargo observamos que sigue muy ligado al tamaño de la muestra y a la cantidad de puntos de serie. Exhibe un comportamiento ajustado siempre que q≥6, excepto cuando la estructura de la matriz es de SC. En este caso, para q= 6 necesita para alcanzar la robustez un tamaño de 16 sujetos para cada grupo. Cuando q= 4 sólo alcanza la robustez si la matriz subyacente es de CA ajustándose para estos niveles (q= 4 o 6) conforme el tamaño de muestra incrementa.
Los procedimientos ρAB , ρAJS, ρG, ρABD y ρAFD, que en Fernández et al. (2002) mostraban su mejor conportamiento cuanto menor era |ρ| y que no dependían del tamaño de muestra, se comportan según lo esperado. ρAB y ρAJS estiman ambos correctamente, mejor el primero (Azzalini y Frigo, 1991), salvo cuando la matriz de desviación es NE y q= 4. ρAJS manifiesta también mal comportamiento cuando la matriz es de CA, q= 4 y nj≤10.
ρG, ρABD y ρAFD se comportan en el modo esperado. La estimación es conservadora (negativa) que, aunque en menor medida que lo era en presencia de autocorrelación de primer orden (Fernández et al., 2002) es inaceptable. En su defensa debemos señalar que su comportamiento es robusto si q≥8 para la matriz NE y ajustado para q= 12 en el resto de las condiciones aquí estudiadas. También en esta nueva situación dependen, al igual que encontraron los autores anteriormente referenciados de q, pero no de nj.
Azzalini y Frigo (1991) muestran la estimación de los procedimientos ρABD y ρAJS cuando el valor del parámetro es cero (r= 0) –sin especificar cómo es la estructura de la matriz–. Podemos advertir que tiene un mejor comportamiento ρAJS que ρABD, y más, cuanto mayor es q, sin influir en absoluto nj. Estos resultados coinciden plenamente con los resultados presentados por nosotros cuando las matrices de dispersión son SC y H-F.
ρPP se comporta de modo similar a ρAB, robusto y ajustado en función de q y nj, salvo cuando la matriz subyacente tiene una estructura CA, ε=.56 y q ≤ 6, en cualquier caso mejor que ρAJS, en desacuerdo con los resultados reportados por Pantula y Pollock (1985). Al igual que encontraron Fernández et al. (2002) depende nj para q= 4 y q= 6.
El procedimiento ρWHS no se comporta de modo regular como hacía en presencia de autocorrelación de primer orden (Fernández et al., 2002), sino que varía en función de qué estructura de no autocorrelación serial es la que subyace a los datos. La estimación es ajustada si la matriz de dispersión es de SC y de H-F; robusta si es de tipo NE y ε=.75, y muy deficiente en el resto de las situaciones investigadas.
En contra de lo expresado por Azzalini y Browman (1991) y de acuerdo con Fernández et al. (2002), ni ρAB ni ρAFD mejoran de modo significativo cuando incrementa el tamaño de la muestra. Son ρJ, y ρPP los estimadores que más dependen de esta variable, lo mismo que sucedía en presencia de autocorrelación serial de primer orden como expresaron los últimos autores mencionados.
Todos estos estimadores son sensibles al maridaje ausencia de autocorrelación-ausencia de esfericidad, siendo los procedimientos más afectados ρWHS, ρG, ρABD, ρAFD y ρPP (en este orden). Precisamente, éstos eran los más sensibles a la heteroscedasticidad intragrupo en el estudio realizado por Fernández et al. (2002).
Coincidimos plenamente con lo expresado por Fernández et al. (2002) en que la estimación no es más acertada cuando el cálculo se realiza desde residuales que desde puntuaciones directas.
Una próxima investigación debería examinar, de una parte, si el procedimiento ρHCH una vez realizadas las estimaciones MLE de ρ y σ2 bajo la H0 y ejecutada la prueba de razón de verosimilitud asociada (Hearne et al., 1983) es suficientemente robusto para decidir que no existe autocorrelación de primer orden cuando la matriz de desviación subyacente a los datos es SC y H-F. De otra parte, debería examinar cómo se comportan estos procedimientos cuando las matrices subyacentes son las aquí utilizadas pero el diseño es no balanceado y cuando la distribución es no normal, al igual que hicieran Fernández y Vallejo (2002) cuando la matriz subyacente es autorregresiva de primer orden. Si las dos condiciones anteriores son satisfactorias, el procedimiento ρHCH sería el estimador más estable y eficiente para detectar la dirección e intensidad de la autocorrelación de primer orden en diseños de Grupos x Ocasiones de medidas repetidas. Así las cosas, una próxima investigación completaría a estas anteriores: ¿qué procedimiento de aquellos que pretenden corregir la autocorrelación serial de primer orden cuando la matriz subyacente a los datos tiene este patrón es más robusto y tiene mayor potencia?. Ambas investigaciones ya están en marcha.
Agradecimientos
Este trabajo ha sido realizado con la ayuda concedida por el MCT-2001-BOS-0410.
Andersen, A.H. Jensen,E.B. y Schou, G. (1981). Two-way analysis of variance with autocorrelated errors. International Statistical Review 49, 153-157.
Anderson, T.W. (1971). The Statistical Analysis of Time Series. New York: Wiley.
Arnau, J. (1999). Reducción del sesgo en la estimación de la autocorrelación en series temporales cortas. Metodología de las ciencias del comportamiento 1(1),25-37.
Azzalini, A. (1984). Estimation and hypothesis testing for collections of autorregressive time series. Biometrika 71, 85-90. Correction: 74 (1987), 667.
Azzalini, A. y Browman, A. (1990). Nonparametric regression methods for repeated measurements. En G.G. Roussas (ED.). Nonparametric Functional Estimation. Kluwer Academic Publisher.
Azzalini, A. y Frigo, A.C. (1991). An explicit nearly unbiased estimate of the AR(1) parameter for repeated measurements. Journal Time Series Analysis 12(4), 273-281.
Bartlett, M.S. (1956). An Intriduction to Stochastic Processes with Special Reference to Methods and Applications. Cambridge University Press.
Cornell, J.E., Young, D.M. y Bratcher, T.L. (1991). An algorithm for generating covariance matrices with specified departures from sphericity. Journal of Statistical Computation and Simulation 34, 240-243.
Daniels, H.E (1956). The aproximate distribution of serial correlation coefficients. Biometrika 43, 169-185.
Fernández, P., Vallejo, G y Escudero, J.R. (2002). Diagnóstico de la precisión de nueve procedimientos para el cómputo de la autocorrelación de primer orden en un diseño de Sujetos x Ocasiones (3xq). Psicothema, 14 (2), 497-503.
Fernández, P. y Vallejo, G (2002). Ausencia de normalidad y desigualdad del tamaño de los grupos. ¿Afecta a la estimación de la autocorrelación? Psicothema 14(4), 861-869.
GAUSS. (1997). The Gauss System. (Vers. 3.2.32). Washington: Aptech Systems, Inc.
Gill, P.S. (1992). A note on modelling the covariance structure of repeated measurements. Biometrics 48, 965-968.
Hearne, E.M., Clark, G.M. y Hatch, J.P. (1983). A test for serial correlation in univariate repeated-measures analysis. Biometrics 39, 237-243.
Jennrich, R.I. y Schluchter, M.D. (1986). Unbalanced repeated-measures models with structured covariance matrices. Biometrics 42, 805-820.
Jones, R.H. (1985). Repeated measures, interventions, and time series analysis. Psychoneuroendocrinology 10(1), 5-14.
Kinderman, A.J. y Ramage, J.G. (1976). Computer generation of normal random numbers. Journal of American Statistical Association 77, 893-896.
Koopmans, T. (1942). Serial correlation and quadratic forms in normal variables. Annals of Mathematical Statistic 13, 14.
Laird, N.M. y Ware, J.H. (1982). Random-effects models for longitudinal data. Biometrics 38, 963-974.
Litlell, R.C., Milliken, G.A., Stroup; W.W. y Wolfinger, R.D. (1996). SAS system for mixed models, Cary, NC: SAS Institute.
Pantula, S.G. y Pollock, K.H. (1985). Nested analysis of variance whith autocorrelated errors. Biometrics 37, 909-920.
Schauer, E.M. y Stoller, D.S. (1966). On the generation of normal random vectors. Technometrics, 4, 278-280.
Schmitz, B. (1990). Univariate and multivariate time series models: The analysis of intraindividual variability and intraindividual relationships. In A. von Eye (Ed.), Statistical Methods in longitudinal Research, 351-386. Boston: Academic Press.
Wilson, P.D., Hebel; J.R. y Sherwin, R. (1981). Screening and diagnosis when within-individual observations are Markov-dependent. Biometrics 37, 553-565.
Wolfinger, R.D. (1996). Heterogeneous variance-covariance structures for repeated measurements. Journal of Agricultural, Biological, and Environmental Statistics 1, 205-230.