DISEÑO DE MEDIDAS REPETIDAS CON DEPENDENCIA SERIAL EN EL ERROR

Paula Fernández y Guillermo Vallejo

Universidad de Oviedo

Para un diseño experimental aleatorio con varias medidas consecutivas a través del tiempo en cada una de las unidades experimentales examinamos dos procedimientos de análisis. Uno de ellos consiste en abordar los datos aplicando el modelo mixto del AVAR con la estructura del error modelada mediante procesos AR. De otro modo, también abordamos el problema desde una perspectiva más general haciendo uso del enfoque multivariado de medidas repetidas. Simulamos datos mediante procedimientos de Monte Carlo para investigar el efecto que el incumplimiento de las asunciones de independencia y esfericidad tiene sobre el grado de sesgadez de los parámetros estimados, sobre la probabilidad empírica de cometer errores Tipo I y sobre la potencia de prueba para cada uno de los procedimientos.

Repeated measures design with error serial dependence. Two analysis procedures for a random experimental design with several consecutives measures through time in each of the experimental units, are examinated in this paper. One of them consists in facing data applying AVAR mixed model with modelated error structure by AR processes. On the other side, the problem also is faced from a more general perspective, using a repeated measures multivariate approach. Data were simulated by Monte Carlo procedures to investigate the effect that have no satisfaction of independence and sphericity assumptions on the biases degree of estimated parametres, on the empirical probability to make type I errors and, on the power of statistical test of the two procedures.

En las investigaciones que se realizan en las ciencias sociales, comportamentales y de la salud, los elementos que componen la población estadística son frecuentemente personas. Debido a las grandes diferencias en experiencia y conocimiento, las respuestas de la gente al mismo tratamiento experimental pueden tener una gran variabilidad. El control de esta fuente de invalidez (interna y/o de conclusión) se logra asignando aleatoriamente los sujetos a los diferentes niveles de tratamiento. Desafortunadamente, para que la aleatorización sea efectiva, o bien disponemos de sujetos muy homogéneos, o bien hacemos uso de tamaños de muestra elevados (Kirk, 1968, p.129). El requerimiento de que el número de sujetos sea alto se hace aún más crítico cuando los niveles de tratamiento o combinaciones resultantes de éstos son numerosos, como en los diseños factoriales. En estos casos, caminos para reducir la varianza del error son el bloqueo y la replicación, que junto con la aleatorización, constituyen la piedra angular en la que se basa el diseño experimental moderno. En fin, en los últimos decenios, un tema de debate sugerente ha sido el desarrollo de una alternativa a los diseños Fisherianos de grupos propios de la investigación experimental clásica. En estas circunstancias, los diseños de medidas repetidas representan una alternativa viable a los diseños de corte transversal, y es que uno de los métodos de investigación más frecuentemente utilizados es tomar observaciones repetidas sobre los mismos sujetos, bien sea en diferentes puntos del tiempo, bien sea bajo diferentes condiciones de una variable determinada. Para el análisis de estos datos se hace uso de alguna de las diferentes variedades de los diseños de medidas repetidas y que hoy se encuentran entre los más comúnmente utilizados en la investigación médica, social y psicológica actual (Barcicowski y Robey, 1984; Keselman y Keselman, 1990; Edwards, 1991; Wallenstein y Fleiss, 1979; Vasey y Thayer, 1987; Keselman, Lix y Keselman, 1993; Keselman, Carriere y Lix, 1993).

Aunque este tipo de diseños no están exentos de dificultades producidas por los efectos de secuencia (efectos de orden y efectos residuales), es meritorio de ellos que acentúan la validez de conclusión estadística debido a una mayor precisión en la estimación de la variable de tratamiento, mejorando de esta manera la potencia de prueba; facilitan la generalización de los efectos del tratamiento debido a la particular presentación de los niveles del mismo, mejorando así la validez externa; reducen drásticamente el tamaño de la muestra y además, en alguna situación particular, permiten elaborar la posible tendencia.

De acuerdo con esto, en los años recientes, los investigadores han enfocado su atención en determinar cual de las estrategias analíticas resulta más apropiada para este tipo de diseños. Tradicionalmente han sido analizados mediante el análisis univariado de la varianza (AVAR) con valores esperados mixtos, en los cuales todos los factores, excepto el factor bloque o sujeto, son considerados fijos. El AVAR asume la independencia de las puntuaciones, que los errores aleatorios de la población siguen una distribución normal y que la matriz de covarianzas sea común para cada uno de los grupos de tratamiento. De todos modos, debido a la naturaleza correlacionada de las medidas repetidas, el AVAR aplicado a estos diseños requiere el cumplimiento de una asunción adicional llamada esfericidad o circularidad. La cual existe sí y sólo sí las varianzas correspondientes a las diferencias entre cualquier par de tratamientos son iguales. La mayoría de los investigadores coinciden en señalar que cumplir la condición de circularidad es difícil de lograr en muchas situaciones, sobre todo cuando trabajamos con datos psicofisiológicos (Wilson, 1967, 1974; Jennings y Wood, 1976; Keselman, Rogan, Mendoza y Brien, 1980) y con datos de investigación en educación y psicología (estudios longitudinales, de crecimiento y aprendizaje clásico) (Davidson, 1972; Wilson, 1975 b; Greenwald, 1976). La consecuencia del incumplimiento de esta asunción es que la razón F del efecto intrasujeto se vuelve excesivamente liberal, se encuentra positivamente sesgada y por tanto el valor real de significación excederá el valor nominal establecido por el experimentador, incrementándose de este modo la posibilidad de capitalizar sobre el azar.

Para solventar este problema se han desarrollado una gran variedad de procedimientos: Mín ε , corresponde al mínimo valor de ε propuesto por Greenhouse y Geisser (1959); , estimador desarrollado por Greenhouse y Geisser , estimador desarrollado por Huynh y Feldt (1976) y toda una gran variedad de ellos que consideran conjuntamente a y , desarrollados por diversos autores (Maxwell y Arvey, 1982; Quintana y Maxwell, 1985, 1994). También en el caso de que existan matrices de covarianza heterogéneas o con tamaños de grupos arbitrarios están disponibles los procedimientos de aproximación general (GA) y aproximación general mejorada (IGA) desarrollados por Huynh (1978) y aproximación general mejorada corregida (CIGA) Algina (1994) y Algina y Oshima (1995). Todos ellos tienen en común que incrementan el valor crítico al estar multiplicados los grados de libertad, del efecto principal y de las interacciones, por algún valor de ε.

Cole y Grizzle (1966) partiendo del hecho de que las observaciones obtenidas en los diseños de medidas repetidas están correlacionadas y, por tanto, son esencialmente de naturaleza multivariada, sugieren que el método adecuado para analizar estos diseños es el procedimiento multivariado. El enfoque multivariado comparte con el enfoque univariado todas las asunciones, excepto que permite a la matriz de varianza-covarianza tener cualquier estructura.

Y es que en muchas investigaciones psicológicas la dependencia serial entre las observaciones tomadas desde una misma unidad de análisis en distintos momentos o intervalos temporales puede llegar a ser de considerable importancia, ya que las relaciones entre las observaciones sólo son entendibles en un cierto contexto dinámico en el que, junto a variables referidas a un mismo momento del tiempo, existen otros efectos desplazados, efectos que se presentan con intensidad creciente cuanto menor es el lapso del tiempo sobre el cual queda definido el modelo. Como se ha puesto de manifiesto en distintas investigaciones (Vallejo, 1986), típicamente, las observaciones registradas desde un mismo sujeto, además de estar gradual y positivamente correlacionadas, presentan una matriz de varianzas-covarianzas entre las medidas repetidas que tiene una estructura Toeplitz (las puntuaciones más próximas presentan una correlación más elevada). De este modo, este fenómeno es contrario a las asunciones que subyacen al modelo mixto del análisis de varianza (AVAR) tal y como fue formulado inicialmente por Scheffé en 1956 que debe asumir que los errores asociados con cada puntuación son independientes. Sin embargo, el cumplimiento de esta asunción, que implica correlación constante o que C*’ΣC* fuese una matriz diagonal, es difícil de lograr en los diseños de medidas repetidas con las observaciones ordenadas sobre el tiempo.

Una forma simple de una estructura de series de tiempo para datos igualmente espaciados es el modelo autorregresivo de primer orden, AR (1). Los datos generados a partir de un proceso estacionario AR (1) presentan varianza constante a través de los t puntos del tiempo y las correlaciones decrecen gradualmente sobre el tiempo. En presencia de dependencia serial positiva el término de error es menor de lo que debiera cometiéndose más errores de Tipo I de los debidos cuando las pruebas estadísticas convencionales son utilizadas (el cual es el más frecuente observado en las Ciencias Sociales y Comportamentales, Maddala, 1977). En presencia de dependencia serial negativa el término de error se incrementa y los tradicionales contrastes t y F cometen más errores de Tipo II.

Este es el patrón usual que presentan las respuestas de los sujetos cuando se registran ordenadamente sobre el tiempo por no utilizar el principio de la aleatorización, bien por imposibilidad, o bien por interés. Cuando esto suceda, las inferencias causales que realizamos con el habitual modelo del AVAR de medidas repetidas deberán ser cuestionadas, pues, si bien es cierto que los parámetros estimados de los efectos principales e interacciones están insesgados, la varianza del error y los correspondientes errores estándar de las medidas están estimados incorrectamente, sesgados en función de los parámetros autorregresivos y/o de las medias móviles. Consecuentemente, los intervalos confidenciales de las medidas observadas pueden sistemáticamente estar subestimados o sobreestimados (Vallejo 1989, pp. 145-147; Suen, Lee y Owen, 1990).

Objetivos

A tenor de lo comentado anteriormente, nos parece de gran importancia estudiar el comportamiento del enfoque multivariado (AMVAR) de medidas repetidas frente al correspondiente univariado, pero con la estructura del error modelada mediante algún proceso que tenga en cuenta la posible correlación serial (AR 1), amén de los procedimientos univariados ajustados: mín ε (mínimo valor de ε); estimador (UVGG) y estimador (UVHF). Por ello, el propósito del presente trabajo, será mostrar los resultados en relación a la probabilidad de cometer errores Tipo I y en relación a la potencia de prueba de los test estadísticos para cada uno de los procedimientos de análisis referidos, el incumplimiento de dos supuestos requeridos por el modelo de diseño experimental de medidas repetidas: esfericidad de la matriz de varianza-covarianza y equicorrelación entre todos los pares de observaciones de una misma unidad experimental, todo ello bajo dos situaciones diferentes de normalidad: normalidad con puntuaciones restringidas y normalidad con puntuaciones sin restringir.

La ausencia de esfericidad ha sido un tema sometido a mucho estudio y debate desde la década de los 60. Nuestro propósito no es, por tanto, estudiarla aisladamente, sino en el contexto de dos distribuciones normales diferentes y en presencia y ausencia de equicorrelación entre todos los pares de observaciones de una misma unidad experimental. También observaremos cual de los dos estadísticos, o , es más robusto en las situaciones antes señaladas.

En relación con la correlación serial, hemos señalado anteriormente, que la ausencia de independencia entre las puntuaciones tomadas desde una misma unidad de análisis cuando es observada repetidamente a través del tiempo, es consustancial en algunas situaciones donde el diseño de medidas repetidas es utilizado. Por este motivo, consideramos de capital importancia tener presente algún planteamiento que modele la correlación serial de los datos, de modo que si ésta resulta ser significativa pueda ser eliminada (de las respuestas efectuadas por los sujetos). Por esta razón, es un objetivo primordial para nosotros, investigar en presencia de autocorrelación el comportamiento del enfoque multivariado de medidas repetidas frente al procedimiento univariado con la estructura del error modelada mediante algún proceso autorregresivo (AR) y frente a los procedimientos univariados ajustados. También nos interesa observar el comportamiento de estos métodos en ausencia de autocorrelación y de esfericidad. Todo ello bajo las dos condiciones de normalidad aludidas.

Parámetros de medias poblacionales y potencias de prueba a priori

Para determinar cómo afecta a la aceptación o rechazo incorrecto de las hipótesis referidas al tratamiento intra y a la interacción para el modelo

En las Tablas 1 y 2 presentamos los vectores de medias υ utilizados y las potencias de prueba teóricas para los dos modelos del diseño estudiado:

a.- Para la condición de H_o para el tratamiento y la interacción. Modelo no aditivo

b.– Para el modelo aditivo

Respecto al cálculo de la potencia de prueba multivariada, así como el cálculo de la potencia de prueba univariada sin corregir la ausencia de esfericidad (ambas a priori) existe mucha literatura al respecto y por ello no nos detenemos en su presentación; no obstante, sí nos parece de capital importancia señalar que para calcular la potencia de prueba a priori univariada corrigiendo la falta de esfericidad hemos seguido el trabajo de Muller y Barton (1989). Estos autores exponen que en el caso en que ε ≠ 1, como sucede en el caso que nos ocupa, la F univariada ya no se distribuye exactamente como F no central, sino de una manera aproximada, es decir, .

Los resultados de Muller y Barton permiten aproximar la potencia para las pruebas de Geisser-Greenhouse y Huynh-Feldt. Por ejemplo, para la prueba de Geisser-Grenhouse lo dicho conduce a utilizar .

Para ello Muller y Barton (1989) aproximan el valor esperado de siguiendo el trabajo de Fujikoshi (1978).

Procedimiento seguido en el cálculo de los datos y en la corrección de la correlación

En cada uno de los experimentos (que más adelante se detallarán) analizamos los datos correspondientes a los modelos aditivo y no aditivo mediante los diferentes procedimientos analíticos como sigue:

– Para el análisis multivariado se ha hecho uso del paquete estadístico SPSS PC 5.0. De los cuatro estadísticos disponibles que este paquete dispensa para recoger el efecto del tratamiento y de la interacción utilizamos la traza de Pillai-Bartlett (Bartlett, 1939; Pillai, 1955) basándonos en los resultados de Olson (1974), Rogan, Keselman y Mendoza (1979) y Bird y Hadzi-Pavlovic (1983) que señalaban que es la más robusta de las pruebas y suficientemente sensible para detectar diferencias en poblaciones con alguna estructura de no centralidad. A pesar de nuestra inclinación por la prueba antes señalada sabemos del estudio de Stevens (1979) que encontró que la traza de Pillai-Bartlett, la Δ de Wilks y la traza de Hotelling-Lawley son esencialmente igual de robustas. De este paquete estadístico también se han recogido los datos de los análisis univariados ajustados , y mín ε.

– Para el análisis univariado de la varianza corrigiendo la correlación están disponibles varios programas (Azzalini, 1984; Jones, 1985 b; Andersen, Jensen y Schou, 1989), con todo, se ha hecho uso del programa estadístico realizado por el profesor Richard H.Jones (1985 b) para los diseños de medidas parcialmente repetidas. Atendiendo al consejo de Azzalini y Frigo (1991) de la necesidad de tomar precaución a la hora de estimar la correlación serial, la elección ha estado subordinada a que este programa utiliza el método de máxima verosimilitud para este fin, y que según los estudios realizados, es el procedimiento que mejor se comporta en la mayoría de las situaciones.

Estos procedimientos de análisis que acabamos de detallar se hicieron bajo cada una de estas dos condiciones:

a) Homoscedasticidad más correlación en la estructura del error

b) Heteroscedasticidad y correlación arbitraria

De cada una de las condiciones efectuamos comparaciones en las siguientes áreas:

1.– Tasas de error de Tipo I

2.– Potencia de prueba

3.– Precisión de las estimaciones efectuadas.

Medidas empíricas de la probabilidad de cometer errores Tipo I se obtuvieron tabulando el número de veces que cada estadístico excede su valor crítico cuando las diferencias en el vector de medias es nula y dividiendo por el número de pruebas efectuadas. La potencia de prueba se derivó registrando el número de veces que la hipótesis nula es debidamente rechazada al nivel α especificado y siempre en un modelo aditivo. Para estimar el grado de sesgo presente en los efectos del diseño se comparó el valor medio de los parámetros estimados, si el estimador es insesgado, entonces el valor promedio se aproximará estrechamente al verdadero valor del parámetro poblacional.

Conclusiones relativas a la eficacia y robustez de los diferentes procedimientos de estimación se obtuvieron comparando los respectivos errores estándar y aplicando el criterio liberal de robustez de Bradley (1978).

Cómputo de los errores estándar: los errores estándar reportados para estudiar las estimaciones empíricas de α son calculados desde , donde p es la probabilidad teórica del error de Tipo I, q es el complementario de p y m es el número de experimentos efectuados. Aquellas estimaciones empíricas de α que estén fuera del intervalo ± 2 desviaciones estándar serán consideradas significativas; si este intervalo se supera por el lado superior las estimaciones serán denominadas liberales, si la estimación es inferior al mínimo valor del intervalo serán consideradas conservadoras.

Cómputo del criterio de robustez de Bradley (1978): de acuerdo con este criterio, y para que una prueba pueda ser considerada robusta, su proporción empírica del error de Tipo I () debe estar contenida en el intervalo 0.5 α ≤ ≤ 1.5 α.

Metodología General

En orden a evaluar los objetivos expuestos, las propiedades de un modelo mixto del AVAR (con errores correlacionados) y las propiedades de un AMVAR de medidas repetidas serán investigadas por medio de datos simulados bajo diferentes situaciones. Las hipótesis a comparar son las referidas a un diseño de medidas parcialmente repetidas (2x8) con ocho vectores de observaciones en cada uno de los dos diferentes grupos, participando 16 sujetos en cada uno de ellos. Para alcanzar este objetivo, desde distribuciones multivariadas normales extrajimos múltiples conjuntos de vectores pseudoaleatorios y^/_ij [ y_ij1, y_ij2,...., y_ijk ] con un vector de medias u^/_j [ u_j1, u_j2,...., u_jk ] y matriz de varianzas-covarianzas Σ.

Generación de datos

a.- Distribución Normal; puntuaciones restringidas: el procedimiento seguido para la obtención de los vectores pseudoaleatorios y’_ij se efectuó en tres fases. En la primera, haciendo uso del método congruencial multiplicativo descrito por Naylor, Balintfy, Burdick y Chu (1966) generamos vectores de variables aleatorias independientes y uniformemente distribuidas entre cero y uno despreciando las puntuaciones que no se encontraban entre ±3 desviaciones estándar. A continuación, haciendo uso del método de Teichroew descrito por Knuth (1969) las variadas uniformes fueron convertidas en vectores de variadas normales Z^/_ij [Z_ij1, Z_ij2,......, Z_ijk]. Finalmente, los vectores de variadas Z’_ij fueron transformados en vectores de observaciones y’_ij (donde y ~N( μ, Σ ) siguiendo el método de Schauer y Stoller (1966) por medio de la ecuación y^/_ij= Tz_ij + μ donde T es una matriz no única y es la descomposición triangular de Σ_j, que satisface la igualdad Σ = LL’ (a menudo llamada factorización de Cholesky o método de la raíz cuadrada (Harman, 1967)). La precisión del procedimiento de normalización comprobada mediante los criterios de sesgo y curtosis aportados por el paquete SPSS PC 5.0 fue enteramente satisfactoria.

b.– Distribución normal; puntuaciones no restringidas: el procedimiento seguido en la obtención de los vectores pseudoaleatorios y’_ij se efectuó en tres fases, las mismas que las descritas en el apartado (a) con la diferencia de que en la primera fase se generaron vectores de variables aleatorias independientes y normalmente distribuidas pero no se desechan las puntuaciones que se encuentran fuera del intervalo ±3 desviaciones estándar. De nuevo, la precisión del procedimiento de normalización comprobada mediante los criterios de sesgo y curtosis aportados por el paquete SPSS-PC 5.0 fue enteramente satisfactoria.

Matrices de varianza-covarianza utilizadas

Las matrices que llamamos ΣI siguen un proceso Markov o autorregresivo de orden uno (en adelante se las señalará como matrices del modelo ΣI) en concreto la matriz ΣI ha sido construida desde:

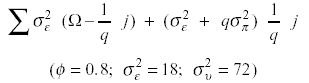
Aquí se asume que el proceso AR es estacionario. Como consecuencia inmediata de la estacionariedad, la varianza es constante para todos los valores de t y la covarianza entre dos cualesquiera términos de error depende únicamente de la distancia temporal entre ellos y no del momento del tiempo a que están referidos.

Las matrices de varianza-covarianza (Σ) que denominaremos como matrices del modelo (ΣII) además de presentar heterocedasticidad sobre el tiempo, los valores situados en las diagonales secundarias también difieren sensiblemente, es decir, tienen una correlación arbitraria.

Tanto las matrices a las que les subyace un modelo AR (I) (ΣI) como las matrices con correlación arbitraria (ΣII) comparten una misma desviación de la esfericidad ε = .46.

Los datos generados a partir de estas matrices nos van a permitir comparar las dos técnicas analíticas aludidas, así como el comportamiento del AVAR de medidas repetidas con la estructura del error modelada mediante algún proceso AR cuando la propiedad de igualdad de las diferentes diagonales de la matriz Σ es parcial o totalmente incumplida.

Apuntar tan sólo lo siguiente: dado que los datos han sido simulados desde poblaciones conocidas y que cada conjunto de observaciones será analizado mediante los procedimientos (AR1, UVGG, UVHF, mín ε y AMVAR), contamos con una situación óptima para determinar el grado de robustez de estos enfoques. De este modo, si un procedimiento es robusto con respecto a sus asunciones, los resultados esperados se obtendrán aunque éstas no se hayan cumplido. Por el contrario, si los supuestos son críticos y el enfoque no tolera desviarse de ellos los resultados diferirán de las conclusiones esperadas.

Experimento 1

Método

En este experimento de simulación Monte Carlo los datos siguen una distribución normal con puntuaciones restringidas entre ± 3 desviaciones estándar, y se han llevado a cabo 2000 análisis para cada uno de los dos modelos de un diseño factorial mixto con una variable entresujetos y una intrasujeto:

1.– Condición de H_o para el tratamiento y la interacción. Modelo no aditivo

2.– Modelo aditivo

Estos 2.000 análisis se han ejecutado para cada una de las dos diferentes construcciones de las matrices de covarianza que conforman los datos:

1.– Homoscedasticidad más correlación en la estructura del error (matrices ΣI). Siguen un proceso autorregresivo de orden uno (ø=.8, ε =.47).

2.– Heteroscedasticidad y correlación arbitraria (matrices ΣII) (ø=.0, ε =.47).

La generación de los datos, la construcción de las matrices de varianza-covarianza así como los test estadísticos mediante los cuales han sido analizados los dos modelos del diseño, ya han sido expuestos en el apartado anterior.

Resultados

Estimación empírica del error de Tipo I para el tratamiento. Modelo no aditivo. Tabla 3

Modelo ΣI: Para un nivel de significación α =.01, los procedimientos AR1 (procedimiento univariado con la correlación corregida) y UVGG mantienen el error en su nivel nominal, el AMVAR también, aunque con una tasa de error empírica muy inferior al nivel teórico ( =.006; a=.01); el procedimiento UVHF es liberal para el criterio del error estándar pero no para el criterio de robustez de Bradley. Para el nivel de significación α = .05 todos los procedimientos mantienen el error en su nivel nominal y para α = .10 también, excepto UVGG que es conservador. El procedimiento univariado ajustado mediante el mínimo valor de épsilon, mín ε, es conservador para todos los niveles de significación utilizados.

Modelo ΣII: Para un α =.01 los procedimientos UVGG, UVHF y AMVAR mantienen la tasa del error controlada por debajo de su nivel nominal. Para el α = .05 y .10 los procedimientos UVGG y UVHF se comportan igual que para el α =.01, sin embargo, el AMVAR es conservador. El procedimiento mín ε y AR1 son conservador y liberal respectivamente para todos los niveles de significación utilizados.

Estimación empírica del error de Tipo I para la interacción. Modelo no aditivo. Tabla 4

Modelo ΣI: Todos los procedimientos mantienen el error en su nivel nominal al α = .01 y α = .05. Para α = .10 el procedimiento UVGG es conservador. El procedimiento mín ε es conservador para todos los niveles de significación utilizados.

Modelo ΣII: El procedimiento mín ε es siempre conservador, y el procedimiento AR1 es siempre liberal para los tres niveles de significación utilizados. Los demás procedimientos se ajustan al nivel nominal si éste es .01; para α = .05 y .10 también, excepto UVGG que es conservador.

Estimación empírica de la tasa de error de Tipo I para la interacción. Modelo aditivo. Tabla 5

Modelo ΣI: Todos los procedimientos mantienen el error en su nivel nominal para todos los valores de α , excepto el procedimiento mín ε, que es siempre conservador.

Modelo ΣII: Los procedimientos AR1 y mín ε son siempre liberal y conservador respectivamente. Para α = .01 los demás procedimientos se ajustan a su valor nominal, para α = .05 y .10 también, excepto UVGG que es conservador.

Estimación empírica de la potencia de prueba. Modelo aditivo. Tabla 6

Modelo ΣI: Los procedimientos univariados ajustados y AMVAR tienen una potencia empírica superior a la potencia teórica ( 1 - = .908, 1 - β = .65 ) y ( 1 - = .44, 1- β = .40 ) para UVGG y AMVAR respectivamente al α = .01) para todos los niveles de significación utilizados, pero son los primeros los que son más poderosos para detectar los efectos del tratamiento. El procedimiento AR1 ( 1 - = .63, 1 - β = .99; α = .01 ), siendo más poderoso que el AMVAR, tiene una potencia inferior al nivel teórico.

Modelo ΣII: Todos los procedimientos tienen una potencia superior al nivel teórico e igualmente elevada.

Los parámetros ε y ø se ajustan casi perfectamente con un valor medio de ε ≈ .45993 y ø ≈ .819 en el conjunto de los 2000 análisis efectuados para este experimento.

Experimento 2

Método

En este experimento de simulación Monte Carlo los datos siguen una distribución normal con puntuaciones sin restringir y se han llevado a cabo 2.000 análisis para cada uno de los dos modelos de un diseño factorial mixto con una variable entresujetos y una intrasujeto:

1.– Condición de H_o para el tratamiento y la interacción. Modelo no aditivo

2.– Modelo aditivo.

Estos 2000 análisis se han ejecutado para cada una de las dos diferentes construcciones de las matrices de covarianza que conforman los datos:

1.– Homoscedasticidad más correlación en la estructura del error (matrices ΣII). Siguen un proceso autorregresivo de orden uno (ø = .8 , ε = .47).

2.– Heteroscedasticidad y correlación arbitraria (matrices ΣII) (ø = .8 , ε = .47).

La generación de los datos, la construcción de las matrices de varianza-covarianza así como los test estadísticos mediante los cuales han sido analizados los dos modelos del diseño, ya han sido expuestos en el apartado anterior.

Estimación empírica del error de Tipo I para el tratamiento. Modelo no aditivo. Tabla 3

Modelo ΣI: Para un α = .01 los procedimientos AR1 y UVHF tienen un comportamiento liberal; UVGG y AMVAR mantienen el error en su nivel nominal siendo este último más conservador. Para un α = .05 todos los procedimientos mantienen el error ajustado y para α = .10 también, excepto UVGG que es conservador. El procedimiento mín ε es siempre conservador.

Modelo ΣII: Los procedimientos UVGG, UVHF y AMVAR mantienen el error en su nivel nominal para todos los niveles de significación empleados. El procedimiento mín ε es siempre conservador y el AR1 siempre liberal.

Estimación empírica del error de Tipo I para la interacción. Modelo no aditivo. Tabla 4

Modelo ΣI: Todos los procedimientos mantienen el error en su nivel nominal para α = .05 y .10; si α = .01, AR1 y UVHF tienen un comportamiento liberal. El procedimiento mín ε siempre es conservador.

Modelo ΣII: Los procedimientos AR1 y mín ε son siempre liberal y conservador respectivamente, los demás procedimientos mantienen el error en su nivel nominal para todos los niveles de significación, excepto UVGG que es conservador para α = .05 y .10.

Estimación empírica del error de Tipo I para la interacción.Modelo aditivo.Tabla 5

Tanto para el modelo ΣI como para el modelo ΣII los resultados son los mismos que para la interacción en el modelo no aditivo.

Estimación empírica de la potencia de prueba. Modelo aditivo. Tabla 6

Modelo ΣI: Los procedimientos univariados ajustados y AMVAR tienen una potencia empírica superior a la potencia teórica para todos los niveles de significación utilizados (1 - = .86, 1- β = .65 y 1 - = .42, 1 - β = .40 para UVGG y AMVAR respectivamente y α = .01), pero son los primeros más poderosos para detectar los efectos del tratamiento. El procedimiento AR1, si bien es más poderoso que el AMVAR, tiene una potencia inferior al nivel teórico (1- = .60, 1 - β = .99; y α = .01).

Modelo ΣII: Todos los procedimientos tienen una potencia superior al nivel teórico e igualmente elevada.

Los parámetros ε y ø se ajustan casi perfectamente con un valor medio de ε ≈ .45993 y ø ≈ .819 en el conjunto de los 2.000 análisis efectuados para este experimento.

Discusión

Recordando los objetivos que nos planteamos y a la luz de los resultados obtenidos, podemos señalar los siguientes puntos:

En presencia de correlación serial elevada y desviación de esfericidad severa (ø= .80 y ε = .47).

Error de Tipo I para el tratamiento

- El AVAR con la dependencia serial corregida (procedimiento AR1) ( = .0139 , α = .01) solamente se ajusta mejor que el AMVAR ( = .006 , α = .01) en situación de normalidad perfecta (puntuaciones restringidas) para todos los niveles de significación, y en este caso, el AR1 ( = .0139 , α = .01) no es mejor que el procedimiento UVGG ( = .0139 , α = .01).

- En presencia de normalidad con puntuaciones sin restringir, más acercado a la realidad, sólo UVGG ( = .013) y AMVAR ( = .007) ajustan el error empírico al teórico para α = .01, y para α = .05 y .10 son el AMVAR y UVHF los que poseen el mejor comportamiento.

- El procedimiento mín ε es conservador en la mayoría de las situaciones apoyando los resultados obtenidos en situación de independencia por Collier, Baker, Mandeville y Hayes (1967), Rogan et al (1979), Keselman y Keselman (1990), Maxwell y Arvey (1982).

- Dado que existe ausencia de esfericidad severa ( ε = .47) el procedimiento UVGG se ajusta mejor que el procedimiento UVHF y el AMVAR sólo para α = .01, siendo estos últimos procedimientos liberal y conservador respectivamente para este nivel de significación. Para α = .05 y .10, UVGG, UVHF y AMVAR mantienen el error en su nivel nominal, pero se ajustan mejor los dos últimos, pecando UVGG un poco de conservador. Dado que q = 8 estamos de acuerdo con las afirmaciones realizadas por Keselman y Keselman (1990), Maxwell y Arvey (1982), Rogan et al. (1979), Keselman, Kesekman y Lix (1995). Barcikowski y Robey (1984) y Looney y Stanley (1989) (todos estos estudios en situación de independencia) que muestran que no hay una clara ventaja entre y la prueba multivariada. Acudiendo a la investigación realizada por Collier y otros (1967), encontramos que su estudio revela que si ε ≤ .75, ofrece una estimación menos sesgada que , pero si contamos con 15 observaciones por grupo, estas estimaciones estaban menos sesgadas y las diferencias entre y se acortaban. Teniendo en cuenta que nosotros contamos con 16 observaciones por grupo y que hemos observado aún una distancia entre estos dos procedimientos, sería bueno en una próxima investigación y atendiendo a la reciente polémica despertada por Lecoutre (1991), comprobar si estas diferencias entre UVGG y UVHF siguen existiendo si sustituimos UVHF por su corrección en esta situación de dependencia, al igual que afirman Algina y Oshima (1995), que en su investigación (situación de independencia) encuentran que experimenta el mejor comportamiento. O si por el contrario confirmamos los hallazgos de Quintana y Maxwell (1994) al respecto y la diferencia entre UVGG y UVHF se presenta menos palpable.

Error de Tipo I para la interacción

- Es indistinto utilizar cualquier procedimiento, ya que no le afecta significativamente la forma de distribución de la normalidad manteniéndose todos los procedimientos dentro del criterio de robustez de Bradley, no obstante es el AMVAR el que experimenta el mejor comportamiento.

- En situación de dependencia, como denominador común y teniendo en cuenta los resultados de esta investigación, es aconsejable utilizar el AMVAR.

Potencia

- Todos los procedimientos tienen una potencia superior a su valor teórico pero son los procedimientos univariados (UVHF > UVGG) más poderosos que el AMVAR.

En presencia de correlación arbitraria y desviación de esfericidad severa (ø= 0.0 y ε = .47).

Error de Tipo 1 para el tratamiento

- Los procedimientos univariados ajustados y AMVAR se acomodan igual de bien al error nominal, en este orden de mejor a peor, UVHF, AMVAR y UVGG. Este resultado es de esperar, ya que los procedimientos UVGG y UVHF corrigen la falta de esfericidad en una situación donde no hay correlación y por tanto no se ven perjudicados, y el AMVAR está operando en una situación óptima para él y no le afecta la ausencia de esfericidad. Estos mismos resultados son encontrados por Keselman et al (1995); Keselman et al (1993), Keselman y Keselman (1990), Maxwell y Arvey (1982).

- El procedimiento AR1 es excesivamente liberal, pero esto es tan sólo un artefacto del procedimiento de análisis, pues al tener la matriz correlación cero y falta de esfericidad, el modelo multivariado tiene en cuenta este hecho, mientras que el AR1 se comporta como el usual modelo mixto del AVAR sin corregir los grados de libertad por la falta de esfericidad.

Error de Tipo I para la interacción

- El procedimiento AR1 siempre es liberal y mín ε siempre es conservador.

- Como denominador común y teniendo en cuenta los resultados de esta investigación, es aconsejable utilizar el AMVAR o UVHF. Compartimos los resultados encontrados en otros estudios puntualizando que Keselman y Keselman (1990) aconsejan utilizar UVHF y Keselman et al (1993) y Keselman y otros (1995) la estrategia combinada /T², después y después T².

Potencia

- Todos los procedimientos tienen la potencia igualmente elevada (siempre es mayor para el AMVAR) y no hay un procedimiento significativamente mejor que otro, lo mismo que encontraron O’Brien y Kaiser (1985), Stevens (1986), Barcikowski y Robey (1974), Rogan et al (1979); Maxwell y Delaney (1990), Keselman et al (1993).

Conclusiones

Teniendo en cuenta la forma de distribución

- Cuando pasamos de puntuaciones restringidas a sin restringir aumenta un poco el error aunque casi nunca es significativo, a excepción del AR1 y UVHF que son liberales para α = .01 en ΣI. En ΣII el error también experimenta un incremento, pero en menor medida que para ΣI.

- Con respecto a la interacción, en los dos tipos de distribución estudiados, en situación ΣI los procedimientos se comportan de la misma forma que lo hacen para el tratamiento, sin embargo para ΣII el AMVAR siempre manifiesta un error igual o mayor que los procedimientos univariados ajustados, siendo liberal para α = .10 si las puntuaciones son restringidas.

- Cuando pasamos de puntuaciones restringidas a sin restringir, la potencia experimenta un pequeño decremento en los dos tipos de matrices utilizados para todos los procedimientos, excepto para AR1 y AMVAR.

- El procedimiento UVGG siempre es más conservador que UVHF tanto para el tratamiento como para la interacción en los dos tipos de distribución estudiados, y conforme incrementa el nivel de significación, mayor es la proporción en que se aleja de éste, ocasionando, a veces, que si para el nivel nominal .01 o .05 mantiene el error en su nivel nominal, para .10 sea conservador.

Teniendo en cuenta la dependencia o independencia entre las puntuaciones

En cuanto al error de Tipo I para el tratamiento: En ausencia de esfericidad severa ( ε = .47) y normalidad con puntuaciones sin restringir (la misma normalidad utilizada en los estudios publicados) UVGG ( = .13) solamente se ajusta mejor que los demás procedimientos para α = .01, lo mismo que es situación de no autocorrelación. Sin embargo el uso de UVHF o AMVAR en situación de dependencia para α = .01 hace que estas pruebas sean liberal y conservadora respectivamente para este nivel de significación, situación en la cual si no hubiese dependencia controlarían el error de Tipo I aunque peor que UVGG. Para α = .05 y α = .10 todos los procedimientos ajustan el error empírico al error teórico tanto en situación de dependencia como de independencia.

En cuanto al error de Tipo I para la interacción: Tanto en presencia como en ausencia de autocorrelación todos los procedimientos aquí estudiados tienen un buen comportamiento.

En cuanto a la potencia: En situación de dependencia, aunque todos los procedimientos tienen una potencia superior a su valor teórico, son más poderosos los procedimientos univariados (de mejor a peor: UVHF, UVGG y AMVAR), al contrario de lo que se esperaría. Cuando no existe dependencia serial, aunque todos los procedimientos tienen una potencia muy alta, es el AMVAR el más poderoso.

Por último señalar que los resultados presentados aquí sólo podrán ser interpretados y generalizados dentro de las limitaciones de este estudio, marcados por el valor de los parámetros utilizados ( μ , Σ , α , β , ø y ε ), tamaño de la muestra, así como por la forma de distribución subyacente. El camino para refutar o confirmar estos resultados es llevar a cabo más estudios de naturaleza similar con otros diseños de medidas repetidas, otras estructuras de Σ y variando los tamaños muestrales.

Algina, J. (1994). Some alternative aproximate tests for a Split Plot design. Multivariate Behavioral Research, 29 (4), 365-384.

Algina, J y Oshima, T.C. (1995). An improved general aproximation test for the main effect in a Split-Plot design. British Journal of Mathematical and Statistical Psychology, 48, 149-160.

Andersen, A.H.; Jensen, E y Schou, G. (1981). Two-way analysis of variance with correlated errors. International Statistical Review, 49, 153-167.

Azzalini, A. (1984). Estimation and hypothesis testing for collections of autorregressive time series. Biometrika, 71 (1), 85-90.

Azzalini, A. y Frigo, A.C. (1991). An explicit nearly unbiased estimate of the AR(1) parameter for repeated measurements. Journal Time Series Analysis, 12, 273-281.

Barcikowski, R.S. y Robey, R.R. (1984). Decisions in single group repeated measures analysis: Statistical test and tree computer packages. The American Statistician 38, 148-151.

Bartlett, M.S. (1939). A note an test of significance in multivariate analysis. Proceedings of. the Cambridge philosophical Society, 35, 180-185.

Bird, K.D. y Hadzi-Pavlovic, D. (1983). Simultianeous test procedures and the choice of a test statistic in MANOVA. Psychological Bulletin, 93, 167-178.

Bradley, J.V. (1978). Robustness?. Brithis Journal of Mathematical and Statistical Psychology, 31, 144-152.

Cole, V.W.L. y Grizzle, J.E. (1966). Applications of multivariate analysis of variance to repeated measures experiments. Biometrics, 41, 505-514.

Collier, R.O.; Baker, F.B.; Mandeville, G.K. y Hayes, T.F. (1967). Estimates of tests size for several tests procedures based on conventional variance ratios in the repeated measures design. Psychometrika, 32, 339-353.

Davidson, M.L. (1972). Univariate versus multivariate test in repeated measures experiments. Psychological Bulletin, 77, 446-452.

Edwards, L.K. (1991). Fitting a Serial Correlation Pattern to Repeated Observations. Journal of Educational Statistics, 16, 53-73.

Fujikoshi, Y. (1978). Asymptotic Expansions for the Distributions of Some Functions of the Latent Roots of matrices in three situations. Journal of Multivariate Analysis, 8, 63-72.

Greenhouse, S.W. y Geisser, S. (1959). On methods in the analysis of profile data. Psychometrika, 24, 95-102.

Greenwald, A.G. (1976). Within-subjects designs: To use or not to use?. Psychological Bulletin, 83 (2), 314-320.

Harman, L.G. (1967). An generaliced simplex for factor analysis. Psychometrica, 20, 173-192.

Huynh, H. (1978). Some approximate test for repeated measurement designs. Psychometrika, 43, 161-175.

Huynh, H y Feldt, L.S. (1976). timation of the Box correction for degrees of freedon from sample data in the randomized block an Split-plot designs. Journal of Educational Statistics, 1, 1582-1589.

Jennings, J.R. y Wood, C.C. (1979). The épsilon adjusted procedure for repeated measures analyses of variance. Psychophisiology, 13, 277-278.

Jones, R.H. (1985 b). Repeated measures, interventions, and time series analysis. Psychoneuroendocrinology, 10 (1), 5-15.

Keselman, J.C. y Keselman, H.J. (1990). Analysing unbalanced repeated measures designs. British Journal of Mathematical and Statistical Psychology, 43, 265-282.

Keselman, J.C.; Lix, L.M. y Keselman, H.J. (1993). The analysis of repeated measurements: A quantitative research synthesis. Paper presented at the Annual Meeting of the American Educational Research Association. Atlanta.

Keselman , H.J.; Carriere y Lix (1993). Testing repeated measures hipotheses when covariance matrices are heterogeneous. Journal of Educational Statistics, Vol 18, 4, 305-319.

Keselam, H.J.; Rogan, J.C.; Mendoza, J.L. y Brien, L.J. (1980). Testing the validity conditions of repeated measures F test. Psychological Bulletin, 87, 479-481.

Keselman, H.J.; Keselman, J.C. y Lix L.M. (1995). The analysis of repeated measurements: Univariate tests, multivariate tests, or both?. British Journal of Mathematical and Statistical Psychology, 48, 319-338.

Kirk, R.E. (1968). Experimental design. Monterey. Ca.: Brooks/Cole.

Knuth, D.E. (1969). Seminumerical Algorithms: The Art of Computer Prograaming. Massachusetts: Addison-Wesley.

Lecoutre, B. (1991). A correction for the ε aproximate test in repeated measures designs with two or more independent groups designs with two or more independent groups. Journal of Educational Statistics, 16, 371-372.

Looney, S.W y Stanley, W.B. (1989). Exploratory repeated measures analysis for two or more groups: Review and update. American Statistics, 43, 200-225.

Maddala, G.S. (1977). Econometrics. New York: McGraw-Hill. (Traducido de la edicción en inglés por la propia editorial).

Maxwell, S.E. y Arvey, R.D. (1982). Small sample profile analysis with many variables. Psychological Bulletin, 92, 778-785.

Muller, K.E. y Barton, C.N. (1989). Approximate power for repeated-measures ANOVA lacking sphericity. Journal of the American Statistical Association, 84, 549-556.

Naylor, H.T.; Balintfy, J.L.; Burdick, D.S. y Chu, K. (1966). Computer Simulation Techniques. New York: John Wiley.

Neyman, J. y Scott, E.L. (1959). Estochastic models of population dynamics. Science, 130, 303-308.

O’Brien, K.G. y Kaiser, M.K. (1985). MANOVA method for analyzing repeated measures designs: An extensive primer. Psychologycal Bulletin, 97, 316-333.

Olson, C.L. (1974). Comparative robustness of six tests in multivariate analysis of variance. Journal of the American Statistical Association, 69, 894-908.

Pillai, K.C.S. (1955). Some new test criteria in multivariate analysis. Annals of Mathematical Statistics, 26, 117-121.

Quintana, S.M. y Maxwell, S.E. (1985). A better than average estimate of ε . Paper presented at the annual meeting of the American Educational Research Association, Chicago.IL, April.

Quintana, S.M. y Maxwell, S.E. (1994). A Monte Carlo comparison of seven ε-Adjustment procedures in repeated measures designs with small sample sizes. Journal of Educational Statistics, 19 (1), 57-71.

Rogan, J.C.; Keselman, H.J. y Mendoza, J.L. (1979). Analysis of repeated measurements. British Journal of Mathematical and Statistical Psychology, 32, 269-286.

Schauer, E.M. y Stoller, S.D. (1966). On the generation of normal random vectors. Technometrics, 4, 279-290.

Scheffé, H. (1959). The analysis of variance. New York: Wiley.

Stevens, J.P. (1986). Applied Multivariate Statistics for the Social Sciences. New Yersey: LEA.

Suen, H.K.; Lee, P.S y Owen, S.V. (1990). Effects of autocorrelation on Single-Subject Single-facet crossed-design generalizability assessment. Behavioral Assessment,12, 305-315.

Vallejo, G. (1986). Aplicación del análisis de series temporales en diseños con N=1: Consideraciones generales. Revista Española de Terapia del Comportamiento, 4, 1-29.

Vallejo, G. (1986). Procedimientos simplificados de análisis en los diseños de series temporales interrumpidas. (modelos estáticos). Revista Española de Terapia del Comportamiento, 4, 114-148.

Vallejo, G. (1989). Regresión de series de tiempo con mediciones igualmente espaciadas. Anuario de Psicología, 43, 126-155.

Vasey, M.W. y Thayer, J.F. (1987). The continuing problem of false positives in repeated measures ANOVA in psychophisiology: A Multivariate Solution. Psychophisiology, 24 (4), 479-486.

Wilson, R.S. (1967). Analysis of automatic reaction patterns. Psychophisiology, 4, 125-142.

Wilson, R.S. (1974). CARDIVAR: The statistical analysis of heart rate data. Psychophisiology, 11, 76-85.

Wilson, R.S. (1975 b). Analysis of developmental data: Comparison among alternative methods. Developmental Psychology, 11 (6), 676-680.

Wallesnstein, S y Fleiss, J.L. (1979). Repeated measurements analysis of variance when the correlations have a certain pattern. Psychometrika, 42 (2), 229-233.

Aceptado el 17 de abril de 1997