Psicothema was founded in Asturias (northern Spain) in 1989, and is published jointly by the Psychology Faculty of the University of Oviedo and the Psychological Association of the Principality of Asturias (Colegio Oficial de Psicología del Principado de Asturias).
We currently publish four issues per year, which accounts for some 100 articles annually. We admit work from both the basic and applied research fields, and from all areas of Psychology, all manuscripts being anonymously reviewed prior to publication.
Psicothema, 1998. Vol. Vol. 10 (nº 1). 1-21
José Muñiz
Universidad de Oviedo
Se analiza la problemática implicada en la medición de las variables psicológicas, y se comentan las soluciones aportadas por los diferentes enfoques psicométricos. En primer lugar, se subraya cómo las dificultades mayores para medir lo psicológico surgen de esa naturaleza especial que tiene lo psicológico: una banda interactiva acotada por una base neurobiológica y un entorno sociocultural. Estas dificultades no fueron óbice para que se haya ido afianzando en psicología una medición rigurosa, cuyos orígenes pueden rastrearse en los trabajos psicofísicos iniciados por Weber y Fechner y que se continúan con el escalamiento psicológico, a partir de los trabajos pioneros de Thurstone. Otra gran línea de desarrollo de la medición sigue el rail de la teoría de los tests, cuyos inicios más rigurosos se ubican en el modelo lineal clásico propuesto por Spearman. A la vez, los teóricos de la medición investigan los fundamentos de ésta, destacando dos líneas de avance: la aproximación clásica, iniciada por Stevens, y el enfoque representacional, surgido a partir de los años sesenta. Se hace especial hincapié en el gran avance que ha supuesto para la psicometría la aparición de la Teoría de Respuesta a los Items, enfoque que viene a dar solución a determinados problemas de la medición que no encontraban una solución apropiada dentro del marco clásico. Además, la teoría de respuesta a los ítems ha generado nuevos avances tecnológicos para el análisis y construcción de los tests, entre los que cabe destacar los Tests Adaptativos Computerizados y la Función de Información. También se comentan los problemas de la validez y el uso de los tests en la práctica.
Psychological measurement. This paper analyzes the principle issues involved in the measurement of psychological variables along with various psychometric solutions to these problems. First, emphasis is placed on the difficulties that arise in psychological measurement due to the unique characteristics inherent in psychological events. These intrinsic limitations, however, were not an obstacle to the development of a rigorous empirical measurement tradition in psychology. This tradition originates in the psychophysical works of Weber and Fechner as well as the classical test theory formulated by Spearman. Moreover, two approaches to measurement theory, the classic one proposed by Stevens and the representational view, investigate the logic and foundations of measurement. This article pays special attention to the psychometric advances brought by Item Response Theory, which resolves some of the problems not appropriately solved within the framework of classical test theory. Item response theory serves as the basis for new technologies to build and assess psychological and educational tests. Finally, test validity and test use are discussed.
A grandes rasgos puede decirse que el objetivo de la Psicología científica es el estudio de la conducta humana y las leyes que la rigen. Como ocurre con cualquier otra realidad, para una comprensión adecuada de la conducta humana hay que entender tanto sus aspectos cualitativos como cuantitativos. A continuación trataré de exponer los aspectos fundamentales implicados en la cuantificación y medición de las distintas variables y factores que manejan los psicólogos, tanto en sus investigaciones como en la práctica profesional. No se trata de una exposición técnica y exhaustiva, la situación y el tiempo no lo permiten, pero sí de subrayar las líneas centrales de la medición de los rasgos psicológicos y de los instrumentos más utilizados para ello, los tests.
Medir es inherente a todas las ciencias, y la Psicología no es una excepción. Si bien los principios generales de la teoría de la medición son aplicables aquí como en el resto de los campos científicos, no es menos verdad que las peculiaridades de los objetos de estudio de algunos de estos campos imponen determinadas especificidades a la lógica general, y ése es el caso de lo psicológico.
El fin general de toda teoría de la medición, trátese de la ciencia que se trate, es estimar los errores aleatorios de las mediciones, pues toda medición, mayor o menor, conlleva un cierto error. Pero seguramente estarán ustedes de acuerdo conmigo en que, por ejemplo, no es lo mismo medir la distancia entre Oviedo y Gijón, cosa de la que se ocupan nuestros colegas físicos, que medir la distancia entre los ovetenses y los gijoneses, entre sus actitudes, valores, personalidad, etc., labor que ocupa a psicólogos, sociólogos, antropólogos y otras ciencias sociales. Por tanto, para entender cabalmente los problemas a los que se enfrentan los psicólogos al medir sus variables de estudio es necesario tener en mente las singularidades de su campo de estudio, de lo psicológico. Diré dos palabras sobre ello, que creo que serán suficientes para comprender por qué a veces la tecnología de la medición psicológica se aleja de la metodología general de la medición utilizada por las ciencias llamadas duras.
Caracterización de lo psicológico
¿Cuáles son las características esenciales que definen a lo psicológico como campo de estudio? La conducta humana fermenta y se desarrolla en una estrecha banda acotada por una base neurobiológica y un entorno sociocultural. El yo psicológico, la individualidad, la consciencia, y por ende la conducta, surgen de la interacción entre la estimulación ambiental y nuestra constitución biológica, pero no se explican ni se agotan en ninguno de estos dos polos, son otra cosa. Precisamente es ése el campo interactivo en el que se mueven los psicólogos, por eso no son ni biólogos, ni neurólogos, ni sociólogos, ni filósofos, son psicólogos. Cuando desde la psicología se explica un determinado fenómeno, ya sea una neurosis, una fobia, el fracaso escolar o la inadaptación laboral, se tienen en cuenta tanto los aspectos neurológicos como los culturales, sociales y educativos, pero su explicación no se agota ni se reduce a ninguno de esos ámbitos. Naturalmente, cuanto más avancen las ciencias afines en las que se apoya la psicología tanto mejor, pero eso no significa abogar por un reduccionismo biológico o cultural. Los avances en el conocimiento del cerebro ayudan sin duda a entender la psique y la conducta humanas, pero es ingenuo y erróneo pensar que, cuán glándula, el cerebro segrega la psique, sencillamente no es así. Algo parecido, salvando las distancias, a lo que ocurre con el software de los ordenadores, que está íntimamente relacionado con el hardware, pero ni se explica ni se reduce a él. ¿Es que alguien en su sano juicio cree que podría entender todo lo que hacen los ordenadores sólo estudiando su hardware? Evidentemente, no, lo cual tampoco significa que pueda prescindir de él.
Igual de erróneo es pensar que la conducta humana venga completamente determinada por el entorno cultural y social; afortunadamente pasaron los tiempos en los que aprendices de ingenieros sociales confiaron en hallar un hombre nuevo con sólo modificar las circunstancias, qué ingenuidad, hoy sabemos de los nefastos resultados y del alto precio pagado. El ambiente externo está ahí, y es una variable clave en la modulación de la conducta humana, pero nunca es el responsable final de ésta, nunca la determina completamente, el único responsable es la persona. Si admitiésemos lo contrario, estaríamos negando de plano la libertad, y, eliminada ésta, no queda lugar para la dignidad y la responsabilidad, que brotan directamente de ella.
Pues bien, en este ámbito peculiar e interactivo, descrito a grandes rasgos, que caracteriza a lo psicológico, no resulta sencillo medir con rigor en sentido clásico, acorde con los axiomas de Hölder (1901) y las propuestas ortodoxas de Campbell (1920, 1921, 1928, 1938, 1940). Sin embargo, los psicólogos miden sus variables y desarrollan sofisticados instrumentos a tal efecto, los más conocidos de los cuales para el público son los tests, si bien los especialistas utilizan una gama mucho más amplia en sus investigaciones e intervenciones. Y miden en campos muy diversos, según su área de especialización, que van desde los procesos más básicos, tales como los Tiempos de Reacción, Potenciales Evocados (Paz y Muñiz, 1989), Tiempo de Inspección, Conductancia de la piel, etc., a los rasgos de personalidad, como Neuroticismo, Depresión, Psicoticismo, Autoconcepto, por citar algunos, o aspectos cognoscitivos, como la Inteligencia, Memoria, Rapidez Perceptiva, Comprensión Verbal, etc., o variables más conectadas con la esfera sociocultural como las actitudes y valores. Y todo ello aplicado a campos de intervención tan variados como la Clínica, Trabajo, Educación, Deporte, Calidad de Vida, Gerontología, Seguridad Vial, etc.
Cada una de esas variables y campos de aplicación tiene su problemática específica, que sería vano intentar tratar aquí, sin embargo, existen unos problemas generales en la medición de lo psicológico que son invariantes a todos los campos y variables mencionadas. En todos los casos, por un lado, hay que estimar la cuantía de los errores cometidos al medir, y, por otro, hay que garantizar que la medición no es baladí, que tiene entidad explicativa y predictiva. En otras palabras, hay que comprobar que las mediciones son fiables y válidas. Además de estas propiedades que deben de reunir todas las mediciones empíricas, los teóricos de la medición se ocupan de analizar y justificar de forma rigurosa el estatus métrico de las mediciones, contemplado a la luz de los avances de la teoría de la medición. De esos tres grandes aspectos generales de la medición, fiabilidad, validez y fundamentos teóricos, es de lo que nos ocuparemos aquí, pero antes de entrar en ellos déjenme que diga unas palabras sobre cómo empezó todo, sobre los orígenes de la medición psicológica.
Inicios de la medición
Los primeros intentos de medir con rigor los atributos psíquicos tuvieron lugar a finales del siglo pasado en los laboratorios alemanes, de la mano de Fechner (Fechner, 1860/1966), pionero de las investigaciones sobre las relaciones entre la estimulación física y las sensaciones psicológicas producidas por ésta. Para estudiar la conexión entre ambos continuos, el físico y el psicológico, Fechner tenía que medir cada uno de ellos y luego establecer la relación correspondiente. Si bien medir los estímulos físicos, tales como el peso, el sonido, la longitud, etc., no suponía ningún problema, se encontró con que no disponía de métodos para medir rigurosamente las sensaciones, para lo cual desarrolló todo un conjunto de ellos, hoy clásicos, denominados métodos psicofísicos indirectos (Baird, 1997; Baird y Noma, 1978; Blanco, 1996; Falmage, 1985; Fechner, 1966; Gescheider, 1985; Muñiz, 1991). Basándose en los trabajos previos de Weber, Fechner estableció que la función que unía la estimulación física con las sensaciones psicológicas suscitadas obedece a una función logarítmica. Ello quiere decir que al aumentar la estimulación física geométricamente las sensaciones lo hacen aritméticamente. O, en otras palabras, que si bien al principio al aumentar la estimulación física aumenta rápidamente las sensaciones, éstas van necesitando cada vez mayor incremento de la estimulación física para experimentar algún aumento. La misma ley había sido observada con anterioridad en el campo de la economía entre el crecimiento de la fortuna y el placer experimentado por el afortunado. Este campo de estudio iniciado por Weber y Fechner se denomina Psicofísica, pues, como su nombre indica, trata de poner en conexión las sensaciones psicológicas con la estimulación física que las suscita. La ley de Fechner ha sido revisada por la Nueva Psicofísica (Stevens, 1961, 1975), que defiende que la función que une ambos continuos, el físico y el psicológico, no es logarítmica sino potencial. Para someter a prueba su hipótesis han propuesto todo un conjunto de nuevos métodos psicofísicos alternativos a los de Fechner, denominados directos.
Leyes Psicofísicas
Función Logarítmica (Fechner): S = C log E
Función Potencial ( Stevens ) : S = K Eb
donde:
S : es la medida de la sensación producida
E : es la medida de la estimulación física
C , K y b son constantes a determinar.
La tradición psicofísica llega hasta nuestros días, constituyendo un campo con grandes implicaciones aplicadas, piénsese, por ejemplo, en la importancia de conocer con precisión los efectos del ruido, la luminosidad, sabores, olores, etc., sobre nuestro sistema perceptivo. En la actualidad gran parte de las investigaciones psicofísicas se llevan a cabo dentro del marco general de la Teoría de la Decisión y de la Teoría de la Detección de Señales (Egan, 1975; Green y Swets, 1966; Swets, 1996), un modelo desarrollado originariamente por los ingenieros para la detección de señales con ruido de fondo, y que se ajusta bien a los humanos considerados como perceptores de señales.
El sistema perceptivo humano es muy peculiar, y la Teoría de la Detección de Señales permite estudiar su funcionamiento bajo diferentes condiciones. El nuestro no es un sistema perceptivo "neutral", pues aunque con determinados invariantes, viene influido en gran medida por las consecuencias de lo percibido, por la "matriz de pagos" asociada a la situación perceptiva, es decir, el mismo sistema perceptivo actúa de distinta forma en función de la situación perceptiva. Esta versatilidad permite investigar y mejorar situaciones aplicadas de todo tipo en las que los humanos tienen que tomar decisiones, siendo clave, por ejemplo, para una racionalización y optimización de las condiciones de trabajo. Piénsese, sin ir más lejos, en situaciones tales como, ¿bajo qué condiciones se maximiza la percepción de piezas defectuosas por un trabajador de control de calidad?, o ¿cuáles son las causas de la accidentabilidad de los trabajadores en puestos aislados? Esas preguntas y otras sólo tienen respuesta correcta cuando se conoce el funcionamiento del sistema perceptivo humano bajo determinadas condiciones.
Nuestras percepciones vienen con frecuencia condicionadas por sesgos cuyo estudio es sumamente importante, tanto a nivel teórico como aplicado, para entender el comportamiento humano. Les citaré un ejemplo clásico de uno de estos sesgos, imagínense una ciudad en la que hay dos hospitales, uno grande, en el que nacen al mes unos doscientos bebés, cien niños y cien niñas aproximadamente, y otro pequeño, en el que sólo nacen veinte al mes, diez niños y diez niñas, más o menos. Si les digo que el último mes en uno de los dos hospitales todos los nacidos fueron niñas, ¿de qué hospital se trata? ¿del grande o del pequeño? No hace falta que contesten aquí en público, pero sé de buena tinta que una parte importante de ustedes por una curiosa razón, bien estudiada por los psicólogos, pensó que se trataba del hospital grande, cuando en realidad es obvio que se trata del pequeño. Si en un caso tan claro como éste ya hay problemas, ¿qué no ocurrirá en nuestra vida diaria? Por ejemplo, ¿por qué los vendedores de lotería agotan rápidamente los números "bonitos" y les cuesta tanto vender los "feos", si es obvio que la probabilidad de que salgan es exactamente la misma para todos? Seguramente dirán algunos de ustedes, "es que la gente no es lógica", y naturalmente tienen razón, la gente no es lógica, y es que la conducta humana responde a las leyes de la psicología y no de la lógica, por eso se ocupan de ella los psicólogos y no los expertos en lógica.
Otro campo de la medición psicológica en la que desembocan estos estudios psicofísicos es la medición de las actitudes, en cuyo caso desaparece el continuo físico (Thurstone, 1927, 1928; Summers, 1970; Triandis, 1971). Medir actitudes es averiguar las preferencias de las personas hacia determinados estímulos, bien sean objetos, ideas o conceptos. Las actitudes constituyen un entramado clave para entender a los humanos, son el cristal a través del que miramos el mundo. Medir su fuerza, conocer su formación, su relación con la conducta y la manera de cambiarlas constituyen campos de sumo interés. Pocos productos salen hoy al mercado sin un estudio concienzudo de las actitudes de los consumidores hacia ellos, y es que la relación calidad/precio no lo es todo, así que no conviene confiar ciegamente en nuestro querido refrán asturiano de que "el buen pan en la masera se vende".
Seguramente todos ustedes tienen alguna experiencia de primera mano de lo difícil que resulta que las personas cambien sus actitudes, y es que están formadas por una trama en la que información, razón y emoción se entretejen de forma compleja. La razón y la información son importantes para que se produzca un cambio de actitudes, pero raramente son suficientes sin apelar a los aspectos emocionales. Por ejemplo, dada la información de la que disponemos hoy acerca de los efectos cancerígenos del tabaco sobre los que fuman y los que les rodean, nadie medianamente informado debería osar tocar un cigarrillo, sin embargo la realidad es muy otra. Los psicólogos que diseñan las campañas antitabaco saben esto y en sus anuncios tratan más bien de tocar la fibra sensible que de introducir nueva información en el sistema. De nuevo aquí observamos que la conducta se aleja de la lógica lineal, y es que como nos recordó certeramente Kant, nada estrictamente recto puede hacerse del torcido leño del que están hechos los humanos.
Esta es a grandes rasgos una de las vías por las que ha entrado la medición en psicología, y cuyo objetivo es el escalamiento de los estímulos, bien sea con referente físico (Psicofísica), o sin él (Actitudes). La otra gran línea de progreso de la medición, mucho más conocida para el público en general es el escalamiento de los sujetos, es decir, los tests. El origen de éstos hay que ubicarlo en las primeras pruebas sensomotoras utilizadas por Galton (1822-1911) en su famoso laboratorio antropométrico de Kensington. El primero en utilizar la palabra "test mental" será James McKeen Cattell (1860-1944) en su artículo "Mental Tests and Measurements" publicado en la revista Mind en 1890. Un giro radical lo constituye la escala individual construida por Binet y Simon (1905) para la medición de la inteligencia, al introducir tareas de carácter más cognoscitivo dirigidas a evaluar aspectos como el juicio, la comprensión y el razonamiento, que según los autores constituían los componentes fundamentales del comportamiento inteligente. Pero la verdadera eclosión de los tests se producirá tras la primera guerra mundial. Cuando Estados Unidos decide entrar en la guerra no dispone de ejército, y la selección y clasificación de los soldados se lleva a cabo confiando en los test Alfa y Beta, diseñados a tal efecto por un comité dirigido por el psicólogo Yerkes. Puesto que los aliados ganaron la guerra, no sabemos que hubiera pasado con los tests si la hubieran perdido, no parecía que los tests hubiesen hecho un mal trabajo, de modo que la industria y las instituciones se volcaron en su uso para todo tipo de fines, especialmente en la selección de personal y en la orientación profesional y educativa. Su uso masivo se extiende hasta nuestros días, siendo difícil encontrar a alguien en las sociedades desarrolladas que primero o después no se tenga que enfrentar a ellos.
En resumen, puede decirse que las dos grandes avenidas de entrada de la medición en Psicología fueron a través del escalamiento de estímulos (Psicofísica y Actitudes) y escalamiento de sujetos (Tests). Como casi toda partición, ésta tiene también algo de arbitrario, pues la mayoría de los modelos podrían generalizarse tanto a estímulos como a sujetos, si bien no faltan problemas específicos que justifiquen la división (Muñiz y Hambleton, 1992). Ambos acercamientos tendrán sus síntesis más clásicas en los textos de Gulliksen (1950) y Torgerson (1958) respectivamente.
Ahora bien, se mida de un modo u otro, ¿qué condiciones deben de reunir esas mediciones para que su uso sea el adecuado? Como ya se ha señalado, básicamente tres propiedades: que sean fiables, que sean válidas, y que estén bien fundamentadas teóricamente. Veamos cada una de ellas.
Fiabilidad
Bajo la denominación genérica de fiabilidad se agrupan todo un conjunto de métodos y técnicas utilizadas por los psicólogos para estimar el grado de precisión con el que están midiendo sus variables. Hace más de cuarenta años, Robert L. Thorndike empezaba su famoso trabajo sobre fiabilidad con estas palabras: "Cuando medimos algo, bien sea en el campo de la física, de la biología o de las ciencias sociales, esa medición contiene una cierta cantidad de error aleatorio. La cantidad de error puede ser grande o pequeña, pero está siempre presente en cierto grado" (Thorndike, 1951, pág. 560). Sus palabras siguen siendo tan ciertas hoy como entonces, pues en lo esencial los problemas de la medición cambian poco, aunque los instrumentos de medida vayan y vengan. Ahora bien, ¿cómo estiman los psicólogos el grado de error que hay en sus mediciones? Veamos la lógica general.
Cuando un psicólogo aplica un test, una escala o cualquier otro instrumento de medida a una persona, obtiene una cierta puntuación, que por razones obvias se denomina puntuación empírica. ¿Cómo estar seguros de que esa puntuación obtenida es la que verdaderamente le corresponde a esa persona en esa prueba? En otras palabras, ¿cuánto error afecta a esa puntuación empírica? Responder estas preguntas es el objetivo de la fiabilidad. Visto así de frente, parecería que tales interrogantes son incontestables, pues, al fin y al cabo, el error cometido, sea el que sea, está diluido en la puntuación empírica y no hay manera de separarlo. Efectivamente, no la hay directamente, como ocurre también con los compuestos químicos. Por ejemplo, sabemos que el agua del mar contiene cierta cantidad de sal, pero para estimar con precisión la cantidad de sal habrá que buscar alguna técnica indirecta que permita la separación. Esas técnicas en el caso de los tests las proporcionarán los estudios de fiabilidad. Nótese que este problema de estimar los errores de medida es común a todas las ciencias, pudiendo decirse que la lógica seguida también lo es, si bien la naturaleza de las variables medidas en las distintas ciencias impone ciertas peculiaridades. Por ejemplo, cuando pesamos un objeto y obtenemos un cierto valor, o aplicamos un test a un sujeto y saca una determinada puntuación empírica, o medimos la distancia entre dos ciudades, en los tres casos se nos plantea la duda de cuánto error estamos cometiendo. Pues bien, para el caso de las variables psicológicas, la propuesta pionera y más fructífera para la estimación de los errores fue hecha ya a principios de siglo por Spearman (1904, 1907, 1913) y la denominamos hoy Modelo Lineal Clásico, dando origen a todo un enfoque general sobre los tests que suele conocerse como Teoría Clásica de los Tests. A partir sobre todo de los años 60-70 aparecen nuevos modelos para abordar la estimación de los errores de medida, agrupándose los más utilizados bajo la denominación genérica de Teoría de Respuesta a los Items.
Modelo Clásico
La propuesta de Spearman para estimar los errores cometidos al medir es un claro ejemplo de cómo a partir de un sencillo modelo y de unas asunciones básicas es posible deducir las fórmulas más complejas para la estimación de los errores de medida.
En primer lugar, Spearman considera que la puntuación empírica de un sujeto en una prueba, puntuación que llamaremos X, consta de dos componentes, la puntuación que verdaderamente le corresponde en esa prueba, que llamaremos V, y un cierto error e. Es decir, formalmente el modelo se podría expresar así:
X = V + e (1)
Donde X es la puntuación empírica obtenida, V la puntuación verdadera y e el error de medida.
Para poder derivar las fórmulas necesarias para el cálculo de la fiabilidad, Spearman añade al modelo tres supuestos y una definición. Asume que 1) la verdadera puntuación de una persona en una prueba sería la que obtendría como promedio si se le aplicase infinitas veces la prueba [ V = E ( X ) ] , 2 ) no hay relación entre la verdadera puntuación de las personas y los errores de medida ( ρve = 0 ), y 3 ) los errores de medida de los tests no están relacionados [ ρ(ej,ek) = 0 ]. Además, define el concepto de tests paralelos como aquéllos que miden lo mismo aunque utilizando distintos ítems. Todo lo cual puede expresarse del siguiente modo:
Modelo Lineal Clásico
Modelo: X = V + e
Supuestos: V = E ( X )
ρve = 0
ρ(ej,ek) = 0
Definición: Dos tests j , k se consideran paralelos si: Vj = Vk y σ2ej = σ2ek
A partir del modelo, mediante los desarrollos correspondientes, que aquí se omiten, va a ser posible llegar a fórmulas operativas para la estimación de los errores (e) , y por ende de las puntuaciones verdaderas (V) de los sujetos. Todas estas deducciones necesarias son lo que conforma el corpus psicométrico de la teoría clásica de los tests, cuya formulación se recoge en textos tan clásicos como los de Gulliksen (1950) o Lord y Novick (1968). Exposiciones sistemáticas pueden consultarse también en Guilford (1936, 1954), Magnuson (1967), Allen y Yen (1979), Thorndike (1982), Crocker y Algina (1986) o Traub (1994). En castellano véase, por ejemplo, Yela (1984), Santisteban (1990), García-Cueto (1993) o Muñiz (1994, 1996a).
Mediante los desarrollos correspondientes se obtiene la fórmula del Coeficiente de Fiabilidad ( ρxx’ ) que permite estimar la cuantía de los errores cometidos al medir. Su fórmula expresa la cantidad de varianza de verdadera medida ( σ2v ) que hay en la empírica ( σ2x ), o en términos de la Teoría de la Información, la proporción señal-ruido del proceso de medición:
ρxx’ = σ2v / σ2x (2)
Lo ideal es que toda la varianza empírica se deba a la verdadera, lo cual ocurriría cuando σ2v = σ2x , en cuyo caso la fiabilidad es perfecta, la prueba mide sin ningún error. El cálculo empírico del valor del coeficiente de fiabilidad no se puede llevar a cabo mediante la fórmula (2), que es meramente conceptual; la estimación empírica puede obtenerse utilizando varias estrategias, entre las que destacan: a) la correlación entre dos formas paralelas del test, b) la correlación entre dos mitades aleatorias del test corregida mediante la fórmula de Spearman-Brown, y c) la correlación entre dos aplicaciones del mismo test a una muestra de personas. Cada uno de estos procedimientos tiene sus pros y sus contras y se ajustan mejor a unas situaciones que a otras. En todos los casos el valor obtenido es un valor numérico entre 0 y 1, indicando a medida que se acerca a 1 que el test está midiendo con precisión. Dado que la fórmula (2) es conceptual, no operativa, en literatura abundan las fórmulas clásicas para la obtención del valor empírico del coeficiente de fiabilidad, entre las que cabría destacar las de Rulon (1939), Guttman (1945), Flanagan (1937), KR20 y KR21 (Kuder y Richardson, 1937), o el popular Coeficiente Alfa (Cronbach, 1951), que expresa la fiabilidad del test en función de su consistencia interna. Una forma alternativa pero equivalente de expresar la fiabilidad de los tests es mediante el Error Típico de Medida, o fiabilidad absoluta.
Se utilice el índice que se utilice, y en cada caso hay razones técnicas para utilizar uno u otro, lo importante es que toda medición lleva asociado un grado de precisión que es empíricamente calculable. Tal vez alguno de ustedes se pregunte por qué se cometen errores al medir, o, en otras palabras, cuáles son las fuentes del error más habituales en la medición psicológica. Es este un asunto exhaustivamente estudiado por los especialistas, que han llegado a clasificar con todo detalle las posibles fuentes de error (Cronbach, 1947; Schmidt y Hunter, 1996; Stanley, 1971; Thorndike, 1951), si bien simplificando bastante puede decirse que son tres las grandes avenidas por las que penetra el error aleatorio en la medición psicológica: a) la propia persona evaluada, que viene con determinado estado de ánimo, actitudes y temores ante el test, ansiedad, o cualquier tipo de evento previo a su evaluación, todo lo cual puede influir en la cuantía de los errores, b) el instrumento de medida utilizado, que con sus características específicas puede influir diferencialmente en los evaluados, y c) la aplicación, corrección e interpretación hecha por los profesionales. Si todo se hace con rigor se minimizarán los errores en todo el proceso, y es precisamente de lo que nos informa la fiabilidad de la prueba, de los errores cometidos. Una vez conocida la cuantía de estos errores, a partir de la puntuación empírica resulta sencillo estimar a cierto nivel de confianza elegido la puntuación verdadera de las personas en una prueba. Si la fiabilidad de una prueba es perfecta (ρxx’ =1), las puntuaciones empíricas y las verdaderas de las personas en dicha prueba coincidirán, pero si no es perfecta las puntuaciones verdaderas de las personas en el test se estiman mediante un intervalo confidencial en torno a la puntuación empírica. La implicación práctica inmediata de todo ello es que si se toman decisiones importantes basadas en las puntuaciones de las personas en los tests hay que asegurarse de que éstos tienen una fiabilidad elevada.
Ahora bien, el modelo lineal clásico informa de la cuantía de los errores, pero no de la fuente originaria de éstos, que asume ignota y aleatoria. Otros muchos modelos se han ocupado de desglosar el error y ofrecer así no sólo la fiabilidad, sino también el origen de los errores (Bock y Wood, 1971; Novick, 1966; Sutcliffe, 1965), pero su complejidad técnico-formal y las complicaciones operativas introducidas, en relación con las ventajas ofrecidas, ha hecho que ninguno haya cuajado en la práctica. Mención especial al respecto merece la Teoría de la Generalizabilidad propuesta por Cronbach y colaboradores (Cronbach, Rajaratnam, Glesser, 1963; Glesser, Cronbach y Rajaratnam, 1965). Mediante el uso de complejos diseños de Análisis de Varianza, este modelo permite hacer estimaciones sobre el tamaño de distintas fuentes de error previamente contempladas en el proceso de medición. El programa de ordenador GENOVA (Crick y Brennan, 1982) ha sido especialmente diseñado para llevar a cabo los cálculos implicados en el modelo. En 1972 los autores publican un exhaustivo tratado (Cronbach, Glesser, Nanda, y Rajaratman, 1972), verdadera biblia del modelo, pudiendo consultarse también exposiciones sistemáticas en Brennan (1983), Crocker y Algina (1986), Shavelson y Webb (1991) o Shavelson, Webb y Rowley (1989); en castellano véase Paz (1994).
Teoría de Respuesta a los Items
A lo largo de este siglo la Teoría Clásica de los tests y sus variantes han ido dando cobertura teórica a la mayoría de las aplicaciones de los tests, y puede decirse que, con sus luces y sus sombras, el balance es claramente positivo (Muñiz, 1994). Ello no quiere decir que no hubiese ciertos problemas y ciertas áreas en las que el enfoque clásico mostrase limitaciones. Las dos más importantes, en las que no voy a entrar aquí, se refieren 1) a la ausencia de invarianza de las mediciones respecto del instrumento utilizado, es decir, bajo el modelo clásico cuando se utilizan tests distintos para evaluar la misma variable no se obtienen directamente resultados en la misma escala, por lo que hay que proceder a equiparar las puntuaciones obtenidas. Y 2) a la dependencia que las propiedades del instrumento utilizado tienen de las propias personas evaluadas, lo cual no es deseable dentro de un marco riguroso de medición.
Aparte de estas dos limitaciones de fondo, en lo que concierne al cálculo de la fiabilidad de los tests, el problema que no encontraba una respuesta adecuada dentro del marco clásico era el de la dependencia entre la cantidad de error y el nivel de las personas en la variable medida. Me explico. Dentro del marco clásico se estima el coeficiente de fiabilidad de una determinada prueba y se asume que es el mismo para todas las personas a las que se aplica la prueba; sin embargo, se ha ido acumulando suficiente evidencia empírica a lo largo de los años que demuestra que el mismo test no mide con la misma precisión a todas las personas, que su precisión está en función del nivel de la persona en la variable medida. Sin salirse del marco clásico la solución más lógica a este problema es calcular diferentes coeficientes de fiabilidad para una prueba en función de los distintos niveles de puntuaciones de las personas evaluadas, lo cual es práctica habitual (Feldt y Qualls, 1996; Lord, 1984; Qualls, 1992; Thorndike, 1951). Si bien es esta una salida enjundiosa al problema, la solución radical y novedosa va a venir de la mano de un nuevo enfoque psicométrico que domina la escena actual de la medición psicológica y educativa denominado Teoría de Respuesta a los Items (TRI).
Bajo la óptica de la TRI la fiabilidad de una prueba pasa a denominarse Función de Información, y es una función matemática continua a lo largo de la escala de las puntuaciones de la prueba (Véase su fórmula matemática más adelante, una vez formulados los modelos de TRI). Es decir, el test ya no tiene un coeficiente de fiabilidad determinado, éste depende, está en función, del nivel de la persona en la variable medida. La fiabilidad se expresa mediante una función (Función de Información) que toma distintos valores según el nivel de la persona en el test. De modo que el mismo test es más fiable para unas personas que para otras, lo cual no es difícil de entender. Piénsese, por ejemplo, en una prueba educativa de cualquier materia que sea realmente difícil, muy difícil, será precisa para evaluar a los muy competentes en la materia, pero todos los que posean conocimientos medios o bajos sacarían (en el caso extremo) un cero, la prueba no discrimina entre ellos, está midiendo sus conocimientos con un error elevado. Es lo mismo que ocurre cuando se desea medir con precisión la altura que salta una persona, hay que ir ajustando el listón a sus posibilidades hasta encontrar justamente lo que es capaz de superar. Mutatis mutandis, lo mismo ocurre para medir con precisión el nivel de una persona en una variable psicológica o educativa. La tecnología evaluativa basada en la teoría de respuesta a los ítems nos ha liberado de la necesidad de tener que utilizar el mismo test con todas las personas para poder compararlas.
Esta nueva conceptualización del error permitida por el marco de la TRI ha llevado a una verdadera revolución en la evaluación psicológica y educativa en los últimos años. Puesto que ya no es necesario utilizar el mismo test para evaluar a todas las personas, se elige aquél que mida con mayor precisión a cada cual, es lo que se ha dado en llamar Tests Adaptativos Computerizados (Olea y Ponsoda, 1996; Renom, 1993; Wainer, 1990), ampliamente utilizados en otros países y en fase embrionaria en el nuestro, aunque algunas compañías multinacionales ya los utilizan en España para certificaciones profesionales.
Tal vez se pregunten ustedes, cómo se procede para elegir la prueba más adecuada para cada persona. La estrategia consiste en buscar aquella prueba cuya dificultad mejor se ajuste al examinado. Para ello se van presentando uno a uno los ítems extraídos de un Banco de ítems y en función de las respuestas, según sean aciertos o errores, se va aumentando o disminuyendo la dificultad de los ítems subsiguientes. De este modo se evita presentar los ítems muy difíciles a las personas con un nivel bajo y los muy fáciles a las de nivel elevado, con el consiguiente ahorro de tiempo y mejora de la motivación y fiabilidad de la prueba. Podría parecer que por esta regla de tres aquéllos que reciben ítems fáciles saldrían favorecidos, pero no hay tal, puesto que cara a la puntuación final no es lo mismo acertar ítems fáciles que difíciles, éstos puntúan más. El uso de estas pruebas está cambiando la forma tradicional de evaluar y en países como Estados Unidos, Holanda, Israel o Canadá, por citar algunos, son de uso generalizado para el acceso a la universidad, al doctorado, o para certificaciones profesionales. Señalar, de paso, que cuando se observan los avances habidos en los últimos años en el campo de la evaluación psicológica y educativa y vemos, por ejemplo, ahora que está en boca de todos, cómo se lleva a cabo la Selectividad Universitaria en España, uno tiene la impresión de estar circulando en un carro de bueyes en tiempos del automóvil y de las autopistas informáticas. Técnicamente nuestro sistema de selectividad es manifiestamente mejorable, y no hacen falta grandes inventos, basta con echar una ojeada alrededor y ver lo que se hace en otros países.
Conceptos básicos de la TRI
Conviene señalar de entrada que los nuevos modelos de TRI no reemplazan al enfoque clásico, sino que mas bien constituyen un excelente complemento, permitiendo resolver problemas que no encontraban solución adecuada en el marco clásico, e impulsando otros campos completamente novedosos de la medición psicológica y educativa. Los orígenes lejanos de la TRI (Muñiz y Hambleton, 1992) pueden rastrearse en los trabajos pioneros de Richardson (1936), Lawley (1943), Tucker (1946), Lord (1952, 1953a) y Birnbaum (1957), si bien su verdadero desarrollo surge a raíz del trabajo de Rasch (1960), y, sobre todo, del libro de Lord y Novick (1968). A partir de entonces se produce una eclosión de publicaciones y de programas de ordenador que permitirán la aplicación de la TRI en la práctica. En la actualidad las fuentes bibliográficas son abundantes (Hambleton, 1990, 1994; Hambleton y Swaminathan, 1985; Hambleton et al., 1991; López-Pina, 1995; Lord, 1980; Muñiz, 1997, 1996b).
Si la piedra angular del enfoque clásico era asumir que la puntuación empírica venía dada por la verdadera más un error aleatorio ( X = V+e ), la TRI va a hacer una asunción ciertamente más restrictiva, a saber, que existe una relación matemática o función que conecta la competencia de los sujetos con la probabilidad de que éstos respondan correctamente a los ítems. En otras palabras, que dada la competencia de una persona en la variable medida, conocemos la probabilidad que tiene de acertar el ítem.
A la función matemática asumida que une los niveles de competencia de los sujetos con las probabilidades de que acierten un ítem es a lo que se denomina Curva Característica del Item (CCI), dado que ciertamente califica, caracteriza al ítem. Cada ítem tendrá la suya propia, su carnet de identidad. Las CCI más habituales adoptan la forma de "S" como las de la figura 1.
En el eje de abscisas aparecen los valores de la variable medida, denominada ( θ ), que está expresada en una escala que va de -∞ a +∞. En ordenadas aparece la probabilidad de acertar el ítem. Ello quiere decir que mediante la CCI sabemos la probabilidad de que las personas con un determinado valor de θ superen el ítem.
La forma exacta de la CCI va a quedar especificada una vez que se elija una función matemática genérica, por ejemplo la curva Normal acumulada, o la Función Logística, entre otras, y se determinen los parámetros correspondientes que la singularizan. Según el tipo de curva que se adopte y el número de parámetros que se contemplen se tendrán los distintos tipos de modelos de TRI. Aunque las posibilidades son casi ilimitadas, a modo de ilustración se presentan a continuación los tres más utilizados en la práctica, que adoptan la Función Logística como Curva Característica:
Modelos Logísticos de 1, 2 y 3 parámetros
Pi( θ ) = eD(θ -bi) / [ 1+eD(θ
-bi) ] (3)
Pi( θ ) = eDai(θ -bi) / [ 1+eDai(θ
-bi) ] (4)
Pi( θ ) = ci + (1-ci) [ eDai(θ
-bi) ] / [ 1+eDai(θ -bi) ] (5)
donde:
θ : representa los valores de la variable medida
Pi(θ) : probabilidad de acertar el ítem para un determinado valor de θ
ai : índice de discriminación del ítem
bi : índice de dificultad del ítem
ci : probabilidad de aciertos al azar
e: base de los logaritmos neperianos (2.7182)
D: constante (cuando D=1,7 los valores se acercan a los generados por la distribución Normal)
La estimación de los parámetros de los modelos se lleva a cabo mediante diversos programas de ordenador existentes a tal efecto (BICAL, BILOG, LOGIST, MULTILOG, RASCAL, ASCAL, etc.), la mayoría de los cuales utilizan procedimientos de máxima verosimilitud o bayesianos. Aparte de los tres modelos incluidos aquí por ser de los primeros formulados y muy utilizados en la práctica, las líneas de investigación más activas trabajan actualmente con modelos bastante más complejos, una buena revisión de los cuales puede consultarse en Van der Linden y Hambleton (1997).
Función de Información del test
Una vez estimados los parámetros del modelo puede calcularse la Función de Información del test, que indica la precisión con la que éste mide a lo largo de la escala de la variable medida:
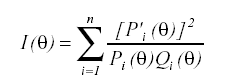
donde:
n : número de ítems del test
Pi( θ ) : valores de las CCI de los ítems
Qi( θ ) : 1- Pi( θ )
P’i( θ ): Derivada de Pi( θ )
En suma, bajo el enfoque de la teoría de respuesta a los ítems los errores cometidos al medir se estiman mediante la Función de Información, que permite especificar la precisión de las mediciones en función del nivel de las personas en la variable medida. Esto supone un avance importante respecto del coeficiente de fiabilidad clásico y abre todo un abanico nuevo de posibilidades en el campo de la medición psicológica y educativa.
Validez
Determinar la cantidad de error de los instrumentos de medida es básico para cualquier ciencia, y hemos visto en líneas generales cómo se lleva a cabo para el caso de los tests desde distintos enfoques psicométricos. Pero el problema de la medición no sólo no acaba ahí, casi puede decirse que empieza, pues una vez que existen garantías de que un instrumento mide con precisión, surge la pregunta clave: ¿son válidas las inferencias hechas a partir de él? Porque no se trata sólo de medir con precisión, además, y, sobre todo, hay que garantizar que las inferencias y decisiones que se hacen basadas en esas mediciones son correctas. Es este el problema de la Validez, concepto clave de la medición en las ciencias sociales. Que las mediciones sean fiables es una condición necesaria, pero no suficiente para que sean válidas. Se puede estar midiendo con gran precisión algo que no tiene ninguna capacidad explicativa o predictiva. No en vano los grandes debates acerca de la utilidad de los tests, las escalas y otras mediciones psicológicas y educativas se centran generalmente en torno al problema de su validez.
Para probar la validez de las inferencias hechas a partir de las pruebas, como ocurre para someter a prueba cualquier otra hipótesis científica, hay que recoger evidencia empírica que corrobore o refute las inferencias. Como señala Messick (1989), la validación de un test abarca todas las cuestiones experimentales, estadísticas y filosóficas por medio de las cuales se evalúan las hipótesis y teorías científicas. En realidad lo que se valida no es la prueba en sí, sino las inferencias hechas a partir de ella. La forma estándar de validar las inferencias es derivar predicciones y contrastarlas con los datos. Con sus luces y sus sombras, el método hipotético deductivo experimental sigue siendo el canon para la validación, eso sí, sin ingenuidades acerca de su infabilidad, y conscientes de sus limitaciones, bien avisados, como estamos, por los ríos de tinta que los teóricos y los filósofos de la ciencia han vertido y vierten al respecto (Block, 1980, 1981; Bunge, 1985; Feyerabend, 1981; Fuentes, 1994; Hanson, 1969; Kendler, 1981; Kuhn, 1962; Lakatos y Musgrave, 1970; Mayor, 1989; Pinillos, 1980; Popper, 1959, 1963, 1972; Staats, 1983; Staats y Mos, 1987; Suppe, 1977; Toulmin, 1972; Yela, 1987, 1994; etc.)
Dentro de ese marco general hay tres procedimientos clásicos y muy utilizados para recabar información empírica probatoria de la validez, denominados Validez de Contenido, Validez Predictiva y Validez de Constructo (Anastasi, 1986; Messick, 1989; Muñiz, 1994; Paz, 1996; Wainer y Braun, 1988).
La validez de contenido tiene un carácter básico, y va encaminada a comprobar que la prueba recoge una muestra representativa de los contenidos correspondientes al campo evaluado. Por ejemplo, si se trata de una escala de actitudes hay que asegurarse que todos los componentes que conforman la actitud están representados en la escala, o si la prueba es de ansiedad, que no se dejan fuera aspectos importantes. No estará de más señalar dentro de este marco profesoral en el que nos encontramos, que este aspecto tan elemental de la validez es descuidado con demasiada frecuencia por los profesores en sus exámenes, al no constituir éstos una muestra representativa de la materia a evaluar, con lo que se abre la puerta al azar en las calificaciones. Personalmente, me sorprenden con frecuencia las ideas tan ingenuas de muchos profesores acerca de la medición educativa, a pesar de la importancia que tiene sobre las vidas futuras de los alumnos. Conscientes de este problema, por ejemplo, recientemente en Estados Unidos el sindicato de profesores más importante (American Federation of Teachers, 1990), junto con otras organizaciones, ha publicado unos estándares técnicos que los profesores deben de seguir en sus evaluaciones.
La Validez Predictiva se centra en la comprobación de que las pruebas predicen aquello para lo que fueron diseñadas. Constituye un aspecto clave en la utilización aplicada de los tests y las escalas en ámbitos en los cuales se toman decisiones importantes para las personas basándose en las pruebas, por ejemplo en el ámbito de la selección de personal, orientación, o situaciones de carácter clínico, por citar algunos. La capacidad predictiva de una prueba suele expresarse mediante su Coeficiente de Validez ( ρxy ), que es la correlación entre las puntuaciones en la prueba (x) y la ejecución en el criterio que se pretende predecir (y). A medida que el valor del coeficiente de validez se acerca a 1 mayor es la capacidad predictiva de la prueba. Cuando se utilizan varias pruebas para predecir un criterio se utiliza como coeficiente de validez la correlación múltiple de las pruebas con el criterio (Ryy’).
La Validez de Constructo, propuesta originariamente por Cronbach y Meehl (1955), trata de asegurar que las variables o constructos medidos, además de capacidad predictiva, tienen entidad y rigor, y se encuentran insertas dentro de un marco teórico coherente. Las formas de recoger evidencia empírica para comprobarlo son en general las utilizadas para comprobar cualquier teoría científica, si bien se han hecho habituales las recogidas de datos a través de una matriz multirrasgo multimétodo (Campbell y Fiske, 1959), o mediante diferentes técnicas de análisis multivariado, entre las que destaca el Análisis Factorial, tanto exploratorio como confirmatorio. En el primer caso suele hablarse de validez convergente-discriminante y en el segundo de validez factorial.
En definitiva, para poder asegurar que una prueba psicológica, educativa o sociológica es válida hay que aportar diferentes tipos de evidencia que lo garantice, no se pueden hacer afirmaciones generales ni definitivas, pues como cualquier otra validación científica, la de los tests es un proceso abierto en el que siempre cabe añadir nueva evidencia empírica que corrobore o refute la pertinencia de las inferencias hechas a partir del test.
El uso de los tests
Un buen ejemplo de este proceso continuo de validación lo constituyen los Tests de Inteligencia. Tras ya casi un siglo de investigación empírica desde que apareciese el primer test propiamente de inteligencia, propuesto por Binet, hoy conocemos bastante bien con qué fines pueden usarse y con cuales no, aunque queden aún varias cuestiones abiertas. Por ejemplo, sabemos que las puntuaciones en los tests de inteligencia son bastante estables a lo largo de la vida de las personas, lo cual no quiere decir que no cambien ni sean modificables (Neisser et al., 1996). Lo que mejor predicen los tests de inteligencia es el rendimiento escolar, con una correlación en torno a 0.50 entre las puntuaciones en los tests de inteligencia y las notas escolares. Ello significaría que la inteligencia explica sólo un 25% del rendimiento escolar. El otro 75% vendría explicado por otros factores tales como persistencia, motivación, interés académico, factores culturales, refuerzos recibidos de los padres y maestros, competencia del profesor, etc. (Neisser et al., 1996). Esta relación positiva entre la inteligencia tal como la miden los tests y el rendimiento escolar tiene como consecuencia que los niños más inteligentes permanecen por término medio más años dentro del sistema educativo, con los efectos positivos que ello conlleva para su éxito social y laboral, por lo que indirectamente los tests de inteligencia también tienen poder predictivo para estos aspectos. La validez de las mediciones de la inteligencia para predecir aspectos de la vida laboral y social de las personas no es que sea muy elevada, en torno al 25%, pero si hay que elegir un sólo predictor, sigue siendo seguramente el mejor del que se dispone. Curiosamente, se conocen más exhaustivamente las predicciones que se pueden hacer a partir de las mediciones de la inteligencia (validez predictiva) que la propia naturaleza de la inteligencia (validez de constructo), existiendo un intenso debate acerca de los factores responsables de las diferencias individuales en inteligencia, en el cual los tres ingredientes básicos son la herencia, el ambiente y los procesos psicológicos básicos, tales como tiempos de reacción, potenciales evocados, tiempo de inspección, capacidad atencional, rapidez de acceso a la memoria, etc. Si bien la teorización sobre la inteligencia ha avanzado notablemente, en comparación los tests con los que se mide no han experimentado grandes cambios (Sternberg y Kaufman, 1996).
Como no podía ser de otro modo, existen tests malos, regulares, buenos y muy buenos, es el profesional en cada caso el que tiene que evaluar la calidad y proceder en consecuencia. Como ocurre con las tecnologías de otros muchos campos del saber, siempre existe la posibilidad de su uso inadecuado, observándose últimamente un interés especial en las organizaciones profesionales por impulsar los aspectos éticos de la práctica, especialmente en lo que a los instrumentos de medida se refiere (Franca-Tarragó, 1996; Keith-Spiegel y Koocher, 1985; Kimmel, 1996; Muñiz, en prensa; Schmeiser, 1992; Schuler, 1982; Stanley, Sieber y Melton, 1996). Debido a que la mayoría de los problemas con los instrumentos de medida psicológicos y educativos provienen en gran parte de su uso inadecuado más que de las propiedades técnicas per se, existe actualmente un debate en curso entre los investigadores y profesionales acerca de la conveniencia o no de incluir las consecuencias del uso de las pruebas dentro del propio marco de la validez (Linn, 1997; Mehrens, 1997; Messick, 1980, 1989, 1995; Popham, 1997; Shepard, 1997).
Señalar, finalmente, que el uso adecuado de los instrumentos de medida no sólo implica que las propiedades técnicas (Fiabilidad y Validez) sean las adecuadas, hay otros aspectos relativos a la propia situación de aplicación que deben de controlarse, tales como la relación examinado-examinador, la ansiedad ante las pruebas (Spielberger y Vagg, 1995), entrenamiento previo, diferencias culturales, deseabilidad social, etc.
Se olvida a veces que los tests psicológicos y educativos representan la posibilidad de juzgar a las personas de forma igualitaria, por sus méritos demostrados, no por criterios como la cuna, la tribu, la familia, la apariencia, las cartas de recomendación, o el juicio subjetivo de supervisores y profesores. Ése fue su espíritu originario, y sigue siéndolo, sus problemas potenciales de uso no deben enmascarar el paso adelante que supone esta filosofía frente a posiciones retrógradas como las mencionadas, tendentes a mantener el statu quo, independientemente de la valía personal.
Teoría de la Medición
Paralelo a la medición empírica de las variables psicológicas, cuya problemática se acaba de exponer a grandes rasgos, existe toda una línea de trabajo más teórica encaminada al análisis del estatus teórico de las mediciones psicológicas, que hinca sus raíces en los trabajos originarios del campo de la Física (Campbell, 1920, 1921, 1928, 1938; Hölder, 1901). Será precisamente un comité de expertos dirigidos por Campbell quienes en 1940 (Campbell et al., 1940) emitan un informe en el que dudan que las mediciones de carácter psicológico y psicofísico reúnan las condiciones exigidas por los axiomas de Hölder (1901). La aproximación de Campbell al problema de la medición era ciertamente restrictiva y tomada al pie de la letra dejaría fuera incluso muchas de las mediciones físicas, por lo cual ya fue criticada por el propio Bertrand Russell (1937). El argumento central de Campbell era que para poder hablar de medición debe de darse un isomorfismo entre la cantidad y las magnitudes de la propiedad a medir; para lo cual había que demostrar que las magnitudes obedecían a los axiomas de cantidad desarrollados por Hölder (1901). Representa una postura de carácter Platónico, bajo cuya óptica las propiedades de la cantidad no son negociables.
Aproximación Clásica
La revolución copernicana en la fundamentación teórica de la medición psicológica vendrá de la mano de Stevens (1946, 1951), al eliminar la restricción de que los números asignados como medidas tengan que obedecer necesariamente a las leyes de la cantidad, abriendo así la posibilidad a otros tipos de escalas (Fraser, 1980). Stevens define la medición como la asignación de números a objetos según determinadas reglas. La flexibilización introducida al permitirse diferentes reglas de asignación extiende el sistema de Campbell y permite el establecimiento de las hoy clásicas cuatro escalas de medición, Nominal, Ordinal, Intervalo y Razón, que vienen definidas por cuatro reglas distintas de asignación de los números a los objetos. Para representar un sistema empírico concreto no habrá por qué utilizar todas las propiedades del sistema numérico. La escala Nominal sólo tiene en cuenta la propiedad de los números igual/desigual, los números actúan aquí como nombres. En la Ordinal, además de igualdad/desigualdad, se tiene en cuenta el orden. La escala de Intervalo además de las anteriores propiedades añade la igualdad/desigualdad de las diferencias, no existiendo un cero absoluto de la escala. Finalmente, en la escala de Razón existe el cero absoluto de la escala e igualdad de razones.
Tras la propuesta de Stevens surgen numerosas clasificaciones de escalas (Coombs, 1952, 1964; Torgerson, 1958), pues no hay ninguna razón para limitar las propiedades a las cuatro mencionadas. Además, la literatura sobre en qué escala vienen medidos los distintos atributos psicológicos y la relación entre el tipo de escala y las operaciones estadísticas permitidas para cada tipo de escala inundan la bibliografía especializada (Gaito, 1980; Lord, 1953b; Michell, 1986; Stine, 1989; Townsend y Ashby, 1984).
Enfoque Representacional
En definitiva, a partir del trabajo pionero de Stevens la medición psicológica no sólo sigue avanzando en el campo empírico, sino que recibe un fuerte empujón en lo que a la evaluación de su estatus teórico se refiere. Tanto la aproximación de Stevens como la de Campbell al análisis teórico de la medición se mueven dentro de un marco clásico, pues, como señala Fraser (1980), si bien Campbell consideraba claves las relaciones empíricas, Stevens subraya las propiedades de la escala. Ambos tratan la relación entre los sistemas empírico y formal como axiomática, y por tanto debe de estar presente para llevar a cabo la medición.
Por el contrario, el nuevo enfoque Representacional sobre teoría de la medición que aparece en los años sesenta (Coombs, 1964; Krantz et al., 1971; Luce y Narens, 1986; Mitchell, 1990; Narens, 1985; Narens y Luce, 1986; Pfanzagl, 1968; Roberts, 1979; Savage y Ehrlich, 1990; Schwager, 1991; Suppes y Zinnes, 1963) se caracteriza fundamentalmente por reconocer explícitamente el papel que juega la teoría en la medición, pasando ésta a formar parte integral de la teoría. Medir es construir un modelo de alguna realidad existente en el mundo. Por tanto, como cualquier otra modelización, implica establecer una correspondencia entre el sistema relacional empírico (el mundo) y un sistema relacional formal (el modelo), de tal modo que se pueda decir que uno representa al otro; si el modelo es numérico entonces la representación se denomina medición (Fraser, 1980). En este contexto los problemas de la medición no son otros que los problemas científicos generales para establecer modelos de la realidad, la medición pasa a ser modelización en la que el sistema relacional formal son los números. Por tanto el problema central a resolver será el de la Representación, es decir, asegurarse que el modelo representa adecuadamente la realidad. Medir es modelizar.
Si bien este enfoque es actualmente dominate entre los teóricos y filósofos de la ciencia, su influencia en la psicología aplicada es escasa, pues como señala Schwager (1991) en una crítica reciente, este elegante enfoque trata de garantizar la representabilidad formal, que es importante, pero no ha aportado hasta la fecha gran cosa a la teoría psicológica y menos aún a la práctica profesional aplicada. Una buena síntesis de los problemas de carácter aplicado aún pendientes de una solución idónea fue expuesta recientemente por Wainer (1993), para una excelente revisión y análisis de los problemas de la medición en psicología puede consultarse el trabajo de Michell (1997).
Estos son, en suma, y a grandes rasgos, algunas de las certezas y de las dudas que ocupan a quienes trabajamos en el campo de la medición psicológica, espero no haberles aburrido demasiado con ellas. En el campo de la medición psicológica quedan muchos problemas teóricos y aplicados por resolver, de modo que no faltará el trabajo de investigación para quienes se dedican a estos menesteres. Esperemos, parafraseando al famoso matemático Hilbert (1902), cuando presentó en París, ya va para un siglo, los 23 problemas más importantes de las matemáticas aún sin resolver, que para tales menesteres contemos entre nosotros con los mejores maestros y los más entusiastas y apasionados discípulos.
Nota
El texto corresponde a la conferencia pronunciada por el autor como lección inaugural del curso académico 1997-1998 en la Universidad de Oviedo.
Allen, M. J. y Yen, W. M. (1979). Introduction to Measurement Theory. Monterrey, CA: Brooks/Cole Publishing Company.
American Federation of Teachers, National Council on Measurement in Education y National Education Association (1990). Standards for teacher competence in educational assessment of students. Washington, DC: Autor.
Anastasi, A. (1986). Evolving concepts of test validation. Annual Review of Psychology, 37, 1-15.
Baird, J. C. (1997). Sensation and judgment: complementary theory of psychophysics. Mahwah, NJ: LEA.
Baird, J. C. y Noma, E. (1978). Fundamentals of scaling and psychophysics. Nueva York: Wiley.
Binet, A. y Simon, T. H. (1905). Methodes nouvelles pour le diagnostic du niveau intellectuel des anormaux. L’Année Psychologique, 11, 191-244.
Birnbaum, A. (1957). Efficient design and use of tests of ability for various decision-making problems (Series Report nº 58-16, Project nº 7755-23). Randolph Air Force Base, TX: USAF School of Aviation Medicine.
Blanco, M. (1996). Psicofísica. Madrid: Universitas.
Block, N. (Ed.) (1980, 1981). Readings in philosophy of psychology (2 vols.). Cambridge, MA: Harvard University Press.
Bock, R. D. y Wood, R. (1971). Test theory. Annual Review of Psychology, 22, 193-224.
Brennan, R. L. (1983). Elements of generalizability theory. Iowa City, IA: American College Testing.
Bunge, M. (1985). La investigación científica. (2ª ed.). Barcelona: Ariel.
Campbell, D. T. y Fiske, A. W. (1959). Convergent and discriminant validation by the multitrait-multimethod matrix. Psychological Bulletin, 56, 81-105.
Campbell, N. R. (1920). Physics. The Elements. Cambridge: Cambridge University Press.
Campbell, N. R. (1921). What is science? (Reimpreso). Nueva York: Dover Publications.
Campbell, N. R. (1928). An account of the principles of measurement and calculation. Londres: Longmans Green.
Campbell, N. R. (1938). Symposium: Measurement and its importance for philosophy. Aristotelian Society, vol. 17 (Suplemento). Londres: Harrison.
Campbell, N. R. et al. (1940). Final Report. Advance Science, núm. 2, 331-349.
Cattell, J. Mck. (1890). Mental tests and measurements. Mind, 15, 373-380.
Coombs, C. H. (1952). A theory of psychological scaling. Engineering Research Bulletin, 34. Ann Arbor, MI: University of Michigan Press.
Coombs, C. H. (1964). A theory of data. Nueva York: Wiley.
Crick, J. E. y Brennan, R. L. (1982). GENOVA. A generalized Analysis of Variance System (FORTRAN IV Computer Program and Manual). Doschester, MA: Computer Facilities, University of Massachusetts at Boston.
Crocker, L. y Algina, J. (1986). Introduction to classical and modern test theory. Nueva York: Holt, Rinehart and Winston.
Cronbach, L. J. (1947). Test reliability: its meaning and determination. Psychometrika, 12, 1-16.
Cronbach, L. J. (1951). Coefficient alpha and the internal structure of tests. Psychometrika, 16, 297-334.
Cronbach, L. J., Glesser, G. C., Nanda, H. y Rajaratnam, N. (1972). The dependability of Behavioral Measurement: Theory of Generalizability for scores and profiles. Nueva York: Wiley.
Cronbach, L. J. y Meehl, P. E. (1955). Construct validity in psychological tests. Psychological Bulletin, 52, 281-302.
Cronbach, L. J., Rajaratnam, N., Glesser, G. C. (1963). Theory of Generalizability: a liberalization of reliability theory. The British Journal of Statistical Psychology, 16, 2, 137-163.
Egan, J. (1975). Signal detection theory and ROC analysis. Nueva York: Academic Press.
Falmage, J. C. (1985). Elements of psychophysical theory. Nueva York: Oxford University Press.
Fechner, G. T. (1860/1966). Elements of psychophysics. Nueva York: Holt, Rinehart and Winston.
Feldt, L. S. y Qualls, A. L. (1996). Estimation of measurement error variance at specific score levels. Journal of Educational Measurement, 33(2), 141-156.
Ferrando, P. J. (1996). Evaluación de la unidimensionalidad de los ítems mediante análisis factorial. Psicothema, 8(2), 397-410.
Feyerabend, P. (1981). Tratado contra el método. Madrid: Tecnos.
Flanagan, J. L. (1937). A note on calculating the standard error of measurement and reliability coefficients with the test score machine. Journal of Applied Psychology, 23, 529.
Franca-Tarragó, O. (1996). Etica para psicólogos. Introducción a la psicoética. Bilbao: Desclée de Brouwer.
Fraser, C. O. (1980). Measurement in psychology. British Journal of Psychology, 71, 23-34.
Fuentes, J. B. (1994). Introducción del concepto de "conflicto de normas irresuelto personalmente" como figura antropológica (específica) del campo psicológico. Psicothema, 6(3), 421-446.
Gaito, J. (1980). Measurement scales and statistics: resurgence of an old misconception. Psychological Bulletin, 87, 564-567.
García-Cueto, E. (1993). Introducción a la psicometría. Madrid: Siglo XXI.
Gescheider, G. A. (1985). Psychophysics: method, theory, and application. Hillsdale, NJ: LEA.
Glesser, G. C., Cronbach, L. J. y Rajaratnam, N. (1965). Generality of scores influenced by multiple sources of variance. Psychometrika, 30, 395-418.
Green, D. M. y Swets, J. A. (1966). Signal detection theory and psychophysics. Nueva York: Wiley.
Guilford, J. P. (1936, 1954). Psychometric Methods. Nueva York: McGraw-Hill.
Gulliksen, H. (1950). Theory of Mental Tests. Nueva York: Wiley (Reimpreso en 1987).
Guttman,L. (1945). A basis for analyzing test-retest reliability. Psychometrika, 10, 255-282.
Hambleton, R. K. (1990). Item response theory: introduction and bibliography. Psicothema, 2, 97-107.
Hambleton, R. K. (1994). Item response theory: A broad psychometric framework for measurement advances. Psicothema, 6(3), 535-556.
Hambleton, R. K. y Swaminathan, H. (1985). Item response theory: Principles and applications. Boston: Kluwer.
Hambleton, R. K., Swaminathan, H. y Rogers, H. J. (1991). Fundamentals of item response theory. Beverly Hills, CA: Sage.
Hanson, N. R. (1969). Perception and discovery. San Francisco: Freeman.
Hilbert, D. (1902). Mathematical problems. Bulletin of the American Mathematical Society, 8, 437-479.
Hölder, O. (1901). Die axiome de quantität die lehre von mass. Berichte ueber die Verhandlugen der Königlich Sachsischen Gessellschaft der Wissenschaften zu Leipzig, Mathematisch-Psysische Class, 53, 1-64.
Intelligence (1997). Número especial dedicado a "Intelligence and Social Policy". Intelligence, 24(1).
Keith-Spiegel, P. y Koocher, G. P. (1985). Ethics in psychology. Professional standards and cases. Nueva York: Random House.
Kendler, H. H. (1981). Psychology: A science in conflict. Nueva York: Oxford.
Kimmel, A. J. (1996). Ethical issues in behavioral research. Cambridge, MA: Blackwell.
Krantz, D. H. Luce, R. D., Suppes, P. y Twersky, A. (1971). Foundations of measurement. Vol 1. Additive and polynomial representations. Nueva York: Academic Press.
Kuder, G. F. y Richardson, M. W. (1937). The theory of estimation of test reliability. Psychometrika, 2, 151-160.
Kuhn, T. S. (1962). The structure of scientific revolutions. Chicago: University of Chicago Press.
Lakatos, I. y Musgrave, A. (Eds.) (1970). Criticism and the growth of knowledge. Londres: Cambridge University Press.
Lawley, D. N. (1943). On problems connected with item selection and test construction. Proceedings of the Royal Society of Edimburg, 61, 273-287.
Linn, R. L. (1997). Evaluating the validity of assessments: the consequences of use. Educational Measurement: Issues and Practice, 16(2), 14-16.
López-Pina, J. A. (1995). Teoría de respuesta al ítem: fundamentos. Barcelona: PPU.
Lord, F. M. (1952). A theory of test scores. Psychometric Monographs, nº 7.
Lord, F. M. (1953a). An application of confidence intervals of maximum likelihood to the estimation of an examinee’s ability. Psychometrika, 18, 57-75.
Lord, F. M. (1953b). On the statistical treatment of football numbers. The American Psychologist, 8, 750-751.
Lord, F. M. (1980). Applications of item response theory to practical testing problems. Hillsdale, NJ: LEA.
Lord, F. M. (1984). Standard errors of measurement at different ability levels. Journal of Educational Measurement, 21(3), 239-243.
Lord, F. M. y Novick, M. R. (1968). Statistical theories of mental tests scores. Reading, MA: Addison-Wesley.
Luce, R. D. y Narens, L. (1986). The mathematics underlying measurement on the continuum. Science, 236, 1527-1532.
Magnuson, D. (1967). Test Theory. Reading, MA: Addison-Wesley. (Traducción española: Mexico: Trillas, 1972).
Mayor, J. (1989). El método científico en psicología. En J. Arnau y H. Carpintero (Comps.). Tratado de psicología general, Vol. I: Historia, teoría y método. Madrid: Alhambra.
Mehrens, W. A. (1997). The consequences of consequential validity. Educational Measurement: Issues and Practice, 16(2), 16-18.
Messick, S. (1980). Test validity and the ethics of assessment. American Psychologist, 35, 1012-1027.
Messick, S. (1989). Validity. En R. L. Linn (Ed.), Educational Measurement. Nueva York: Macmillan.
Messick, S. (1995). Validity of psychological assessment. American Psychologist, 50, 741-749.
Michell, J. (1986). Measurement scales and statistics: a clash of paradigms. Psychological Bulletin, 100, 398-407.
Michell, J. (1990). An introduction to the logic of psychological measurement. Hillsdale, NJ: LEA.
Michell, J. (1997). Quantitative science and the definition of measurement in psychology. British Journal of Psychology, 88, 355-383.
Muñiz, J. (1991). Introducción a los métodos psicofísicos. Barcelona: PPU.
Muñiz, J. (1994). Teoría clásica de los tests. Madrid: Pirámide. (2ª ed.).
Muñiz, J. (1996a). Fiabilidad. En J. Muñiz (Coor.), Psicometría. Madrid: Universitas.
Muñiz, J. (Coor.). (1996b). Psicometría. Madrid: Universitas.
Muñiz, J. (1997). Introducción a la teoría de respuesta a los ítems. Madrid: Pirámide.
Muñiz, J. (en prensa). Aspectos éticos y deontológicos de la evaluación psicológica. En Evaluación Psicológica, Madrid: TEA Ediciones.
Muñiz, J. y Hambleton, R. K. (1992). Medio siglo de teoría de respuesta a los ítems. Anuario de Psicología, 52, 41-66.
Narens, L. (1985). Abstract measurement: the theory of numerical assignment. Psychological Bulletin, 99, 166-180.
Narens, L. y Luce, R.D. (1986). Measurement: the theory of numerical assignment. Psychological Bulletin, 99, 166-180.
Neisser, U. et al. (1996). Intelligence: knowns and unknows. American Psychologist, 51(2), 77-101.
Novick, M. R. (1966). The axioms and principal results of classical test theory. Journal of Mathematical Psychology, 3, 1-18.
Olea, J. y Ponsoda, V. (1996). Tests adaptativos informatizados. En J. Muñiz (Coor.), Psicometría. Madrid: Universitas.
Paz, M. D. (1994). Teoría de la Generalizabilidad. En J. Muñiz, Teoría clásica de los tests. Madrid: Pirámide.
Paz, M. D. (1996). Validez. En J. Muñiz (Coor.), Psicometría. Madrid: Universitas.
Paz, M. D. y Muñiz, J. (1989). Potenciales evocados y tiempos de reacción. Psicothema, 1, 97-117.
Pfanzagl, J. (1968). Theory of measurement. Nueva York: Wiley.
Pinillos, J. L. (1980). Problemas actuales de la psicología científica. Análisis y Modificación de Conducta, 6, 11-12.
Popham, W. J. (1997). Consequential validity: right concern-wrong concept. Educational Measurement: Issues and Practice, 16(2), 9-13.
Popper, K. R. (1959). The logic of scientific discovery. Londres: Hutchinson.
Popper, K. R. (1963). Conjectures and refutations. Nueva York: Harper.
Popper, K. R. (1972). Objective knowledge. Oxford: Clarenton Press.
Qualls, A. L. (1992). A comparison of score level estimates of the standard error of measurement. Journal of Educational Measurement, 29(3), 213-225.
Rasch, G. (1960). Probabilistic models for some intelligence and attainment tests. Copenhagen: The Danish Institute for Educational Research.
Renom, J. (1993). Tests adaptativos computerizados. Barcelona: PPU.
Richardson, M. W. (1936). The relationship between difficulty and the differential validity of a test. Psychometrika, 1, 33-49.
Roberts, F. S. (1979). Measurement theory. Reading, MA: Addison Wesley.
Rulon, P. J. (1939). A simplified procedure for determining the reliability of a test by splithalves. Harvard Educational Review 9, 99- 103.
Russell, B. (1937). The Principles of Mathematics (2ª Ed.). Nueva York: Norton.
Santisteban, C. (1990). Psicometría. Teoría y práctica en la construccción de tests. Madrid: Norma.
Savage, L. W. y Ehrlich, R. (Eds.). (1990). Philosophical and foundational issues in measurement theory. Hillsdale, NJ: LEA.
Schmeiser, C. B. (1992). Ethical codes in the professions. Educational Measurement: Issues and Practice, 5-11.
Schmidt, F. L. y Hunter, J. E. (1996). Measurement error in psychological research: lessons from 26 research scenarios. Psychological Methods, 1(2), 199-223.
Schuler, H. (1982). Ethical problems in psychological research. London: Academic Press.
Schwager, K. W. (1991). The representational theory of measurement: an assessment. Psychological Bulletin, 110(3), 618-626.
Shavelson, R. y Webb, N. (1991). Generalizability theory. Beverly Hills, CA: Sage.
Shavelson, R. Webb, N. y Rowley, G. L. (1989). Generalizability Theory. American Psychologist, 44 (6), 922-932.
Shepard, L. A. (1997). The centrality of test use and consequences for test validity. Educational Measurement: Issues and Practice, 16(2), 5-8.
Spearman, C. (1904). The proof and measurement of association between two things. American Journal of Psychology, 15, 72-101.
Spearman, C. (1907). Demonstration of formulae for true measurement of correlation. American Journal of Psychology, 18, 161-169.
Spearman, C. (1913). Correlations of sums and differences. British Journal of Psychology, 5, 417-126.
Spielberger, C. D. y Vagg, P. R. (Eds.) (1995). Test anxiety. Theory, assessment and treatment. Washington, DC: Taylor and Francis.
Staats, A. W. (1983). Psychology’s crisis of desunity. Philosophy and method for a unified science. Nueva York: Praeger.
Staats, A. W. y Mos, L. P. (Eds.) (1987). Annals of theoretical psychology. Vol. 5. Nueva York: Plenum Press.
Stanley, B. H., Sieber, J. E. y Melton, G. B. (Eds.). (1996). Research ethics. A psychological approach. Lincoln, NE: University of Nebraska Press.
Stanley, J. C. (1971). Reliability. En R. L. Thorndike (ed.), Educational Measurement. Washington. DC: American Council on Education.
Sternberg, R. J. y Kaufman, J. C. (1996). Innovation and intelligence testing: the curious case of the dog that didn’t bark. European Journal of Psychological Assessment, 12(3), 175-182.
Stevens, S. S. (1946). On the theory of scales of measurement. Science, 103, 677-680.
Stevens, S. S. (1951). Mathematics, measurement and psychophysics. En S. S. Stevens (Ed.), Handbook of experimental psychology. Nueva York: Wiley.
Stevens, S. S. (1961). To honor Fechner and repeal his law. Science, 133, 80-86.
Stevens, S. S. (1975). Psychophysics: introduction to its perceptual, neural, and social prospects. Nueva York: Wiley.
Stine, W. W. (1989). Meaningful inference: the role of measurement in statistics. Psychological Bulletin, 105, 1, 147-155.
Summers, G. F. (Ed.) (1970). Attitude measurement. Chicago: Rand McNally.
Suppe, F. (Ed.). The structure of scientific theories. Urbana, IL: University of Illinois Press.
Suppes, P. y Zinnes, J. L. (1963). Basic measurement theory. En R. D. Luce, R. R. Bush y E. Galanter (Eds.), Handbook of mathematical psychology. Vol. I, págs. 1-76. Nueva York: Wiley.
Sutcliffe, J. P. (1965). A probability model for error of classification, I: General considerations. Psychometrika, 30, 73-96.
Swets, J. A. (1996). Signal detection theory and ROC analysis in psychology and diagnostics: collected papers. Mahwah, NJ: LEA.
Thorndike, R. L. (1951). Reliability. En E. L. Lindquist (Ed.), Educational Measurement (págs. 560-620). Washington, DC: American Council on Education.
Thorndike, R. L. (1982). Applied Psychometrics. Boston: Hougton Mifflin.
Thurstone, L. L. (1927). A law of comparative judgment. Psychological Review, 34, 273-286.
Thurstone, L. L. (1928). Attitudes can be measured. American Journal of Sociology, 33, 529-554.
Torgerson, W. S. (1958). Theory and methods of scaling. Nueva York: Wiley.
Toulmin, S. (1972). Human understanding. Princeton: Princeton University Press.
Townsend, J. T. y Ashby, F. G. (1984). Measurement scales and statistics: the misconception misconceived. Psychological Bulletin, 96, 394-401.
Traub, R. E. (1994). Reliability for the social sciences: Theory and applications. Londres: Sage.
Triandis, H. C. (1971). Attitude and attitude change. Nueva York: Wiley.
Tucker, L. R. (1946). Maximum validity of a test with equivalent items. Psychometrika, 11, 1-13.
Van der Linden, W. J. y Hambleton, R. K. (Eds.). (1997). Handbook of modern item response theory. Nueva York: Springer-Verlag.
Wainer, H. (Ed.). (1990). Computerized adaptive testing: a primer. Hillsdale, NJ: LEA.
Wainer, H. (1993). Measurement problems. Journal of Educational Measurement, 30(1), 1-21.
Wainer, H. y Braun, H. I. (Eds.). (1988). Test validity. Hillsdale, NJ: LEA.
Yela, M. (1984). Introducción a la teoría de los tests. Madrid: Facultad de Psicología, Universidad Complutense.
Yela, M. (1987). Toward a unified psychological science. En A. W. Staats y L. P. Mos (Eds.), Annals of theoretical psychology. Vol. 5. Nueva York: Plenum Press.
Yela, M. (1994). El problema del método científico en psicología. Anuario de Psicología, 60, 3-12.
Aceptado el 10 de octubre de 1997