Psicothema was founded in Asturias (northern Spain) in 1989, and is published jointly by the Psychology Faculty of the University of Oviedo and the Psychological Association of the Principality of Asturias (Colegio Oficial de Psicología del Principado de Asturias).
We currently publish four issues per year, which accounts for some 100 articles annually. We admit work from both the basic and applied research fields, and from all areas of Psychology, all manuscripts being anonymously reviewed prior to publication.
Psicothema, 1998. Vol. Vol. 10 (nº 2). 491-507
Emelina López González
Universidad de Málaga
La colinealidad entre los predictores de un modelo de regresión es un problema muy frecuente, sobre todo en el ámbito de las ciencias humanas. Existen diferentes procedimientos para su diagnóstico, pero sin embargo no es una situación que tenga un fácil tratamiento, excepto cuando se haya producido por el uso de datos u observaciones erróneas, en cuyo caso se puede resolver omitiéndolas. La posibilidad de introducir nuevos datos, o de seleccionar otro subgrupo de predictores quizá sea la mejor solución, pero en la mayoría de las ocasiones no es posible, dada la situación experimental. Existen, sin embargo, algunos métodos alternativos que permiten utilizar la información original y que posibilitan seguir explicando un porcentaje similar o mayor de la variabilidad de la variable respuesta. En esta línea abordamos aquí, entre otros, el Análisis de Componentes Principales y la Regresión Ridge. Sobre ellos apuntamos las implicaciones en el tratamiento de la colinealidad derivadas de sus características matemáticas, considerando, al mismo tiempo, las ventajas e inconvenientes de su utilización.
Treatment of collinearity in multiple regression analysis. Collinearity among predictors in a regression model is a very frequent problem, specially in Human Sciences. There are several procedures for diagnosing collinearity, but it cannot be easily solved. However, if it is caused because wrong data or observations were collected, then it is possible to omit them and, in this way, the problem is automatically solved. To introduce new data or to select another subgroup of predictors is perhaps the best solution, but this procedure is not always possible to apply because of experimental setting. However, there are some alternative methods which allow to use previous information and to explain a similar percentage of response variability (or even greater than the preceding one). In this work, we use -among other procedures- Principal Component Analysis and Ridge Regression. We remark their implications for collinearity treatment as a consequence of their mathematic properties and, simultaneously, we expose which are the advantages and disadvantages when these procedures are used.
La colinealidad es un problema del análisis de regresión que consiste en que los predictores del modelo están relacionados constituyendo una combinación lineal. Este hecho tiene consecuencias fundamentales en el modelo de regresión: si los predictores se encuentran en combinación lineal, la influencia de cada uno de ellos en el criterio no puede distinguirse al quedar solapados unos con otros; no se consigue una explicación del fenómeno en cuestión; los pronósticos no son nada fiables, puesto que otra combinación de predictores introducida en el modelo variando el orden, produce predicciones en el criterio contradictorias; no se realiza una selección adecuada del orden de entrada de los regresores en el modelo, y un largo etcétera. Es un problema que no tiene fácil solución, ya que en definitiva se trata de pedirle a la muestra de datos más información de la que posee (Peña, 1987). Para corregirla sólo cabe actuar en alguno de los siguientes sentidos:
- Eliminar variables predictoras, con lo que se reduce el número de parámetros a estimar.
- Incluir información externa a los datos originales.
Si se opta por el primero de ellos, se trata de suprimir, o bien ciertas variables que se encuentren altamente correlacionadas, o bien algunas combinaciones lineales mediante el Análisis de Componentes Principales aplicado a la regresión. La segunda alternativa conduce a trabajar con estimadores contraídos o bayesianos.
En ambas opciones se sustituyen los estimadores mínimo cuadráticos de los coeficientes de regresión por estimadores «sesgados». Estos procedimientos forman parte de la regresión sesgada, no lineal, pero que sigue cumpliendo el supuesto de los mínimos cuadrados. Además, estos estimadores, a pesar de ser sesgados, tienen un error cuadrático medio mucho menor, que es lo que se pretende para corregir la colinealidad.
Eliminación de alguna variable predictora
Es la solución mas cómoda ya que únicamente hay que eliminar aquellos predictores correlacionados con otros. Los estimadores que resultan tienen una varianza de error menor, como pasamos a demostrar.
Supongamos que la verdadera relación entre predictores y criterio es:
Y = β1 X1 + β2 X2 + u (1)
donde consideramos que todas las variables tienen media cero. Si eliminamos una variable explicativa y estimamos el modelo, tenemos:
Y = ![]() 1
X1 + ε (2)
1
X1 + ε (2)
El estimador ![]() 1
en (1) es centrado con varianza
1
en (1) es centrado con varianza
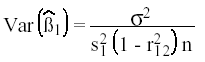 (3)
(3)
y ![]() 1en
(2) es:
1en
(2) es:
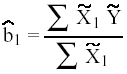
Como ![]() 1
es sesgado, su esperanza es
1
es sesgado, su esperanza es
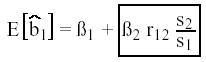 (4)
(4)
en donde la parte recuadrada corresponde al sesgo, y su varianza será:
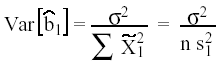 (5)
(5)
Al comparar los dos estimadores, ![]() 1
y
1
y ![]() 1
, el error cuadrático medio de
1
, el error cuadrático medio de ![]() 1
es su varianza (3) y el de
1
es su varianza (3) y el de ![]() 1
será:
1
será:
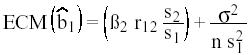
Para que ![]() 1
tenga un error cuadrático medio menor, se tiene que cumplir que:
1
tenga un error cuadrático medio menor, se tiene que cumplir que:
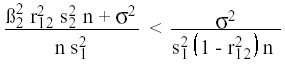
o sea:
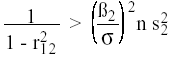 (6)
(6)
luego si r12 se aproxima a uno, el error cuadrático
medio de ![]() 1
es menor que el de
1
es menor que el de ![]() 1
. Con ello se obtienen efectivamente estimaciones sesgadas (4) del efecto de
X1, habiendo eliminado del modelo la variable X2, pero
en definitiva estas estimaciones son preferibles si se quiere corregir la colinealidad.
1
. Con ello se obtienen efectivamente estimaciones sesgadas (4) del efecto de
X1, habiendo eliminado del modelo la variable X2, pero
en definitiva estas estimaciones son preferibles si se quiere corregir la colinealidad.
Para saber cuándo se debe eliminar un predictor del modelo, tengamos en cuenta que (6) se puede escribir como:
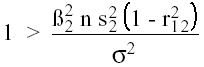 (7)
(7)
Si en esta expresión sustituimos β2 y σ2 por sus estimadores, se obtiene el cuadrado del estadístico t que se utiliza para contrastar la significación del parámetro estimado. En ese caso se pueden eliminar las variables cuyo estadístico t sea menor que uno, lo que hace que la media cuadrática de error disminuya.
No hay que olvidar, como señalan Gunst y Mason (1980) y Hoerl (1985), que antes de decidir la eliminación de variables sería bueno analizar si el problema de la colinealidad es un asunto de la muestra concreta con la que se trabaja o de la población a la que pertenece dicha muestra. Si ocurre lo primero y se elimina algún regresor, no cabe duda de que en el caso de replicación con otra muestra distinta los efectos de haber eliminado algún predictor se dejarán notar, sobre todo porque quizá en esa nueva muestra el predictor eliminado podría ser relevante en lugar de redundante. El verdadero problema de colinealidad existe si se produce en la población. Gunst y Mason (1980) comentan estrategias para detectar ambas situaciones.
Al margen del procedimiento de eliminación de predictores colineales, se han desarrollado un conjunto de técnicas para saber el efecto de la omisión de variables predictoras. Se trataría de una omisión «a priori», distinta a la señalada arriba, en la que no se espera a construir el modelo (1) y luego omitir un predictor para que quede como (2), sino que se define el modelo omitiendo desde el principio alguna variable predictora. Bajo este punto de vista Mauro (1990) señala un procedimiento para estimar el efecto de la variable omitida en la variable respuesta en función de otro predictor sesgado que permanece en el modelo y que no es omitido. Pero para que así sea, es necesario que la variable omitida cumpla una de estas tres condiciones:
(a) que tenga un efecto sustancial sobre la variable criterio (que presente una correlación alta con la misma);
(b) que esté altamente correlacionada con el predictor que permanece en el modelo y a partir del cual se va a deducir el efecto de la variable omitida; y
(c) que no esté correlacionada con el resto de los predictores del modelo.
Análisis de Componentes Principales
El análisis de Componentes Principales (ACP) merece una mención algo más amplia que indicar únicamente su utilidad como tratamiento para la colinealidad. Está considerado como una técnica de Análisis Multivariante dentro de las conocidas como Métodos Factoriales, entre las que se encuentra también el Análisis Factorial de Correlaciones y el Análisis de Correspondencias (Batista y Martínez, 1989). Dentro del marco de la Regresión, constituye una importante alternativa al ajuste por mínimos cuadrados junto con la Regresión Ridge (Harris, 1985: 86).
Fundamentalmente es una técnica de reducción de variables (Riba, 1989) con la intención de describir una estructura de covariación, aproximándose a ella desde una nueva perspectiva en función de las dimensiones subyacentes en los datos, que quedan reflejadas en unas nuevas variables. Por tanto, el objetivo del análisis de componentes principales aplicado a la regresión es construir un conjunto de nuevos predictores, los componentes principales, a partir de los ya existentes, por medio de combinaciones lineales de precisamente esas variables regresoras originales, de tal forma que con esos mismos datos de partida, las variables independientes se transforman en otras a través de las relaciones lineales existentes entre ellas.
Desde un punto de vista descriptivo y geométrico, se considera que las variables predictoras X definen un subespacio euclídeo de p dimensiones (tantas como variables). Los valores observados para un individuo en cada una de las variables X son las coordenadas que permiten trasladar al espacio un vector que represente a dicho sujeto. La representación de todas las observaciones define la nube de puntos (representativa de la relación entre el criterio y los predictores); lógicamente la tendencia de esa nube será igual a la suma de las varianzas de las variables predictoras. En este análisis, por tanto, se realiza una rotación de ejes: se buscan unos ángulos de rotación de forma que los nuevos ejes, ortogonales entre sí, maximicen sucesivamente la varianza de la proyección de la nube sobre cada uno de ellos. Estos ejes son los componentes. Las proyecciones del vector de cada sujeto sobre dichos ejes son los valores que tiene ese sujeto en las nuevas variables.
Gráficamente, la diferencia entre la regresión por componentes y la regresión lineal común es que en la regresión la recta o superficie que ajusta la nube de puntos minimiza la suma de cuadrados de los residuos de los puntos a la recta en una dirección paralela a la variable respuesta o criterio; en el ACP, donde no se privilegia a una variable frente a otra, puesto que se estudia la interdependencia del conjunto en lugar de la dependencia de unas variables con respecto a otras, el interés se centra en la recta o componente representativa de la interrelación, por lo que la minimización se refiere a las desviaciones cuadráticas ortogonales a dicha componente, y no a las paralelas de una dirección prefijada (Batista y Martínez, 1989: 97). Dicho de otro modo, el ACP de un grupo de p variables originales genera p nuevas variables, los componentes principales, CP1, CP2, ... , CPp, donde cada componente principal es una combinación lineal de las variables originales, de tal forma que
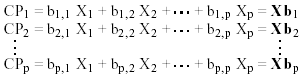 (8)
(8)
o bien expresado matricialmente:![]() (8), donde cada columna de B contiene los coeficientes para cada componente
principal (CP es una matriz sencilla, no un producto de matrices).
(8), donde cada columna de B contiene los coeficientes para cada componente
principal (CP es una matriz sencilla, no un producto de matrices).
Los p nuevos componentes principales deben cumplir estas dos restricciones:
(a) ser independientes;
(b) proporcionar sucesivamente la máxima información posible del criterio, en el sentido de que la varianza que explica CP1 sea la mayor de todas las variables posibles CPi linealmente transformadas, ortogonales a CP1 , y así sucesivamente.
Dado que la multiplicación de una variable por una constante "c" proporciona una nueva variable que tiene una varianza c2 veces mayor que la varianza de la variable original, solo necesitamos utilizar de forma arbitraria los mayores coeficientes para conseguir que S2CP sea arbitrariamente mayor (Harris, 1985: 236-237). Es decir, únicamente nos importan las magnitudes relativas de los coeficientes definidos en cada CP. Con objeto de eliminar la solución trivial, bi,1 = bi,2 = ... = bi,p = ∞ , se necesita que los cuadrados de los coeficientes empleados en cada CP sumen la unidad, es decir:
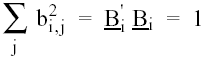 (9)
(9)
y así,
![]()
(10) donde S es la matriz de varianzas y covarianzas de las variables originales. Para evitar la indeterminación del sistema, se pone la restricción antes señalada: B'i Bi = 1 . Como queremos encontrar el máximo valor de (10), sólo tenemos que calcular los valores extremos condicionados, lo cual se resuelve utilizando los multiplicadores de Lagragian, maximizando la función auxiliar siguiente (Batista y Martínez, 1989: 44):
![]()
En esta función se deriva respecto a bi y luego se iguala a cero:
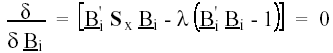
lo cual proporciona el sistema:
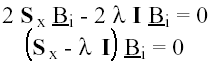
Si multiplicamos este sistema por B'i , estamos teniendo en cuenta la restricción B'i Bi = 1 , y efectivamente: λi = B'i Sx Bi = S2CPi, de modo que el valor de λi es el máximo que buscábamos. Pero para encontrar λi y Bi , necesitamos resolver el sistema anterior de forma que en él la ecuación [ Sx - λ I ] Bi tenga solución no trivial, o lo que es lo mismo, la matriz [ Sx - λ I ] sea singular, que su determinante sea cero: [ Sx - λ I ] = 0 .
Desarrollando el determinante, se tiene la ecuación característica, vector latente o eigenvector, que proporciona los valores de λ o raíces latentes de Sx (eigenvalores). Si se sustituye el valor de λi calculado en el sistema, se obtiene el eigenvector Bi asociado a λi , cuyos elementos serán los coeficientes de la combinación lineal óptima. A este respecto se puede consultar el artículo de Cliff (1988), donde precisamente se argumenta sobre el tamaño de los eigenvalores de este eigenvector que proporciona la mejor combinación.
Cada λi es la varianza de las variables que forman combinación lineal por medio de los coeficientes que proporciona el eigenvector, o sea, la varianza de cada componente principal. Si surge una λi igual a cero, es señal de que hay una dependencia lineal entre las variables originales (Harris, 1985: 237). Este proceso se lleva a cabo en la construcción de cada uno de los CPj.
El segundo CP se halla de forma que maximice la varianza residual (la que queda después de eliminar la varianza explicada por el primer CP ). Finalmente B'i Sx Bj , que es la covarianza entre CPi y CPj , es cero para i ≠ j. Entonces tenemos que la ortogonalidad entre los vectores característicos de Sx se cumple desde el momento en que los diferentes CP no están correlacionados.
En suma, las dos restricciones que deben darse en este análisis, ambas aplicadas a cada vector latente, son:
- B'i Bi = 1 (unitario)
- B'i + 1 Bi = 0 ( Bi + 1 ortonormal a bi ); las p ecuaciones de CP resultantes al determinar los pesos o coeficientes de los p componentes, se resumen en la expresión:
S = V Λ V' (11)
donde V es la matriz ortonormal V' V = V V' = I que tiene en sus columnas los p eigenvectores asociados a las p raíces latentes de la matriz de varianzas y covarianzas S, y Λ es una matriz diagonal cuyos elementos son las raíces latentes de la matriz S:
Λ = diag ( λ1, λ2, ..., λp > λK=1 )
La ecuación (11) sería ahora
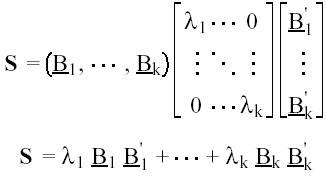 (12)
(12)
de forma que descompone la matriz S en una suma de las p matrices Bi B'i ; es decir, esta solución ha llevado a diagonalizar la matriz S de covarianzas de las variables originales.
Si nos encontramos con predictores en forma estandarizada, la correspondiente matriz de covarianzas es R y se llega al mismo algoritmo. La diferencia está en que las raíces latentes de R son distintas a las obtenidas diagonalizando S, y un cambio de una a otra no se puede obtener con transformaciones sencillas. En Batista y Martínez, (1989: 46) se puede completar este argumento. También en Chatterjee y Price (1991: 157-163) se trabaja la Regresión con Componentes Principales de forma estandarizada.
Veamos qué ocurre una vez hallados los p componentes principales, si éstos se introducen en el modelo de regresión en lugar de las k variables explicativas (normalmente k > p). Como es lógico pensar, los estimadores que se obtienen no están centrados, pero es posible que presenten menos varianza, que en definitiva es lo que se pretende para corregir la colinealidad. Llamando (CP)p a la matriz de p x n datos de estos componentes, el modelo es:
Y = ( CP )p β*c + U (13)
donde ahora las p variables explicativas elaboradas son ortonormales, y la estimación de cada coeficiente ya no supone más que:
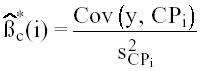
Para obtener los coeficientes ![]() c
de los predictores originales, como ( CP )p =
c
de los predictores originales, como ( CP )p = ![]() Vp , donde Vp es la matriz k x p de eigenvectores asociados
a los p valores de las raíces latentes de S, sustituimos en (13):
Vp , donde Vp es la matriz k x p de eigenvectores asociados
a los p valores de las raíces latentes de S, sustituimos en (13):
![]() (14)
(14)
y así queda expresado el modelo con los predictores originales.
Un problema que presenta este análisis es que el número de CP que se construye es arbitrario, en consecuencia es muy importante en el entorno del análisis de regresión que la construcción de los CP tenga una explicación lógica, en el sentido de que no surjan contradicciones con el fenómeno que se esté investigando, lo que realmente no es tan sencillo cuando los CP son artificiales (Mosteller y Tukey, 1977). A este aspecto se refiere McCallum (1970) en su artículo sobre la ortogonalización artificial en el análisis de regresión. Para este autor precisamente esa pérdida de información por la falta de centralización de los predictores no supone un problema, ya que lleva a una mejor estimación de los parámetros del modelo de regresión ‘original’, incluso para variables creadas artificialmente con información añadida, con lo que según McCallum, sigue siendo mejor el remedio. No obstante, hay opiniones distintas: para Batista y Martínez (1989: 92), este análisis es práctico cuando se tiene un elevado número de variables predictoras, en cuyo caso puede ser incluso imprescindible como una buena estrategia de selección de las variables que sean más ortogonales entre sí.
En el tratamiento del análisis de componentes principales con paquetes estadísticos, en general, es conveniente considerar algunas referencias para hallar raíces y vectores latentes. En el paquete SPSS, por ejemplo, no se distingue entre la técnica de Componentes Principales y el modelo de Análisis Factorial. En BMDP sí encontramos un análisis de componentes principales en el programa 4R que resulta cómodo y sencillo.
En López (1995a) se desarrolla un ejemplo de regresión por componentes principales utilizando el programa 4R de BMDP y se comentan los resultados comparando esta regresión con otros análisis de regresión más comunes, como la regresión stepwise o la regresión múltiple sin procedimiento definido de selección de variables. Al final del presente trabajo presentamos un ejemplo detallando la información que se obtiene en la salida de un análisis con el programa 4R, y comparamos la regresión de componentes principales que corrige la colinealidad, con aquellas donde no se contempla que las relaciones lineales entre predictores supongan un problema para el modelo de regresión.
Hay textos que apuntan algunos otros detalles del análisis de componentes aplicado a la regresión: Grenn (1977) analiza cómo afectan los cambios en los parámetros a la bondad del ajuste, o lo que él define como ‘sensibilidad de los parámetros’ en la regresión múltiple y en la regresión con componentes principales; Harris (1985) presenta un capítulo completo haciendo hincapié en las consecuencias de la utilización del ACP; Stone y Brooks (1990) relacionan el ACP con la regresión continua. Por último señalamos las referencias de Riba (1989); Peña (1987: 415-419); Batista y Martínez (1989); Weisberg (1985: 199-202) y Drapper y Smith (1981: 327-329).
Estimadores contraídos
Hemos apuntado antes que una segunda alternativa para corregir la colinealidad consiste en añadir información externa a los datos. Las dos técnicas desarrolladas para este propósito son la Regresión de Stein y la Regresión Ridge. Ambas combinan la sensibilidad de la regresión múltiple y el propósito de reducir el error cuadrático medio para corregir la colinealidad.
Algunos autores como Darlington (1978), no recomiendan estos
estimadores para trabajos con modelos teóricos, ya que los estimadores
resultantes son sesgados y además no permiten ni el uso de intervalos
confidenciales, ni pruebas de significación. Sin embargo estos estimadores
corrigen el efecto de la colinealidad, en el sentido de que contraen
el tamaño de ![]() .
Veamos cómo se produce.
.
Veamos cómo se produce.
Sabemos que ![]() es:
es:
![]() = ( X' X )-1 X' Y
= ( X' X )-1 X' Y
con lo que el estimador contraído será:
![]() c
= ( X' X + K Q )-1 X' Y (15)
c
= ( X' X + K Q )-1 X' Y (15)
donde K es una constante y Q es una matriz definida positiva. Si aplicamos en (15) la fórmula de la inversión de matrices, tenemos que:
![]() c
= ( I - K ( X' X + K Q )-1 Q-1 )
c
= ( I - K ( X' X + K Q )-1 Q-1 ) ![]() (16)
(16)
lo que indica que estamos disminuyendo el valor de ![]()
A partir de aquí consideramos estimadores contraídos aquellos que cumplen (16) , pudiendo ser de dos tipos:
a) Si tomamos Q= X' X , entonces
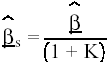 (17)
(17)
éstos son los estimadores de Stein, que además de proporcionar una media cuadrática menor, el coeficiente de determinación resultante para validar el modelo es igual al que se obtiene utilizando los estimadores normales. Para un estudio más detallado conviene remitirse a la referencia inicial de Stein (1960), así como a algunas interpretaciones posteriores: Cattin (1981); Darlington (1978) y Drapper y Smith (1981).
b) Si tomamos Q = I, entonces
![]() R
= ( X' X + K I )-1 X' Y (18)
R
= ( X' X + K I )-1 X' Y (18)
obteniendo así los estimadores ridge que pasamos a ver a continuación.
Regresión Ridge
La Regresión Ridge supone un procedimiento de ajuste de los estimadores mínimo cuadráticos con el objetivo de reducir su variación. Constituye toda una alternativa a la estimación mínimo cuadrática, y además proporciona una evidencia gráfica de los efectos de la colinealidad en la estimación de los coeficientes de regresión. Dicho procedimiento se encuentra dentro del grupo de las regresiones parciales o sesgadas, consideradas como no lineales.
Hemos señalado que una de las consecuencias de la colinealidad era el aumento de la varianza asociada a la estimación de los coeficientes de regresión, con lo que los coeficientes estimados pueden no brindar la suficiente confianza o incluso ser erróneos si los vectores predictores no son ortogonales. La Regresión Ridge proporciona unos nuevos estimadores que garantizan precisamente minimizar dicha varianza, de forma que constituye un método alternativo cuando las variables explicativas son altamente no ortogonales.
El nombre de Regresión Ridge se debe a los trabajos desarrollados por Hoerl (1964) al aplicar el Análisis Ridge a las superficies de respuesta de segundo orden que resultan de utilizar muchos regresores. Dicho análisis ridge y la regresión ridge presentan procesos matemáticos similares. La primera exposición detallada de esta regresión se encuentra en el artículo de Hoerl y Kennard (1970), donde se contempla el proceso de cálculo de los estimadores ridge, su expresión canónica, el gráfico de trazo ridge y el análisis gráfico. Posteriormente, Marquardt y Snee (1975) llevan a cabo una buena aplicación de todos estos procesos con un estudio detallado sobre la interpretación y validación del modelo.
Tal y como se encuentra ya desarrollada esta técnica, supone un aproximación que responde a dos problemas: (a) detección, y (b) estimación de la multicolinealidad, cuando hay sospechas de su existencia. En general, la filosofía que subyace en este análisis es la comparación entre la estimación mínimo cuadrática ‘común’, que vamos a denotar por MCO (Mínimos Cuadrados Ordinarios), y la estimación mediante la estrategia del ‘trazo ridge’. Ambas alternativas son enfrentadas y estudiadas en relación a lo que sería la verdadera estimación de los coeficientes (en términos de esperanzas) que es desconocida. En este proceso de comparaciones y estudio de propiedades se llega a demostrar que en los casos de colinealidad, los estimadores resultantes por el trazo ridge se encuentran más próximos o concentrados a los verdaderos valores de los parámetros de regresión, y por lo tanto dichas estimaciones presentan una varianza menor a la que poseen las estimaciones por MCO (incrementada por el efecto de la colinealidad). Estos nuevos estimadores ridge son parciales o sesgados, pero dado que su media cuadrática es menor, son más estables, en el sentido de que no van a estar afectados por las variaciones de los datos (la demostración de que los estimadores ridge se distribuyen con una media cuadrática de error menor se encuentra en Hoerl y Kennard (1970)). El criterio para decidir cuándo los estimadores ridge son preferibles a los estimadores MCO depende de los valores de los verdaderos coeficientes del modelo de regresión, pero como éstos son desconocidos, la regresión ridge sería útil cuando se sospecha de una extrema colinealidad (Chatterjee y Price, 1991: 182).
Los estimadores ridge de los coeficientes de regresión
se pueden hallar alterando ligeramente las ecuaciones normales. Esta modificación
consiste en añadir pequeñas cantidades positivas a la diagonal
de la matriz de datos X’X, siempre y cuando ésta se encuentre
en forma estandarizada. Por esta razón X’X está referida
como W’W (con la notación de Gunst y Mason, 1980), o bien ![]() '
'
![]() . No obstante,
ya que en la notación original de Hoerl y Kennard (1970) aparece como
X’X, así lo haremos aquí, dejando claro que debe estar
estandarizada.
. No obstante,
ya que en la notación original de Hoerl y Kennard (1970) aparece como
X’X, así lo haremos aquí, dejando claro que debe estar
estandarizada.
Tomando entonces la forma estandarizada del modelo
Y = β1 X1 + β2 X2 + ... + βp Xp + ε
las ecuaciones de estimación para el modelo ridge con p variables explicativas son:
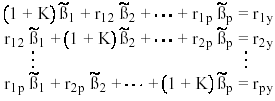 (19)
(19)
donde rij es la correlación simple entre los predictores i y j, y r iy es la correlación entre la iésima variable explicativa y la variable respuesta. La solución a (19) es el grupo de coeficientes de regresión ridge estimados:
![]() *1
, ... ,
*1
, ... , ![]() *p
*p
Esta notación de ![]() *i
no se identifica con los parámetros de componentes principales. Ponemos
el asterisco para diferenciarlos de los parámetros obtenidos por MCO.
*i
no se identifica con los parámetros de componentes principales. Ponemos
el asterisco para diferenciarlos de los parámetros obtenidos por MCO.
Como puede verse, el parámetro fundamental que distingue
la regresión ridge de la regresión MCO es K, denominado estimador
ridge. Nótese que cuando K es cero, los ![]() *i
coinciden con los estimadores de MCO (sería el caso de ortogonalidad
de la matriz de datos X, como veremos).
*i
coinciden con los estimadores de MCO (sería el caso de ortogonalidad
de la matriz de datos X, como veremos).
Mientras que en MCO los estimadores de los parámetros se definen como:
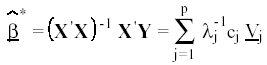 (20)
(20)
siendo cj = V'j X' Y, el estimador ridge se expresa tal que
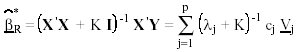 (21)
(21)
donde aparece la suma de la pequeña constante K, cuyo valor oscila entre 0 y 1, añadida a los elementos de la diagonal de X’X. Las propiedades de la expresión (21) aplicadas a la regresión ridge se encuentran en Marquard y Snee (1975).
El efecto de K en los vectores latentes de (21) se puede entender
de la siguiente manera: si se suma una pequeña cantidad K a las raíces
latentes pequeñas, λi , la influencia de los vectores
latentes que identifican multicolinealidades puede ser bastante reducida. Si
K es suficientemente pequeño, sólo las raíces latentes
muy pequeñas se alterarán sustancialmente en (21). Por ejemplo:
los vectores latentes con raíces grandes o medianas tendrán aproximadamente
la misma influencia en ![]() * que en
* que en ![]() *R, ya que para estas raíces:
*R, ya que para estas raíces:
![]() (22)
(22)
Una de las razones más importantes que confirma la
utilidad del análisis ridge es que eligiendo un K lo suficientemente
pequeño, no sólo se reducen los efectos de la colinealidad, sino
que el estimador ridge está próximo a ![]() , que es el verdadero estimador mínimo cuadrático. La razón
teórica por la que se justifica es:
, que es el verdadero estimador mínimo cuadrático. La razón
teórica por la que se justifica es:
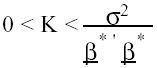 (23)
(23)
sin embargo, para que se cumpla (23), K debe encontrarse en un intervalo que garantice esta condición, y esto no se puede fijar ya que desconocemos los verdaderos parámetros de (23). Cattin (1981) propone una fórmula alternativa para K tal que K = 1/F, donde F es el estadístico obtenido por MCO.
Numerosos autores han tratado de solucionar este problema y
parece ser que el trazo ridge resulta ser la estrategia de más fácil
manejo e interpretación. Consiste en construir un gráfico con
el objeto de encontrar un valor de K que proporcione un grupo de coeficientes
con mínima varianza de error y que cumplan la solución mínimo
cuadrática. Los valores de K para los cuales los coeficientes se estabilizan
son el grupo de coeficientes deseados. Si las variables predictoras son ortogonales,
entonces los coeficientes cambiarán muy poco (serán muy estables),
lo que indica que la solución mínimo cuadrática de MCO
es buena para el ajuste. Es decir, para diferentes valores de K en un intervalo
de 0 a 1, se hacen distintas estimaciones de los parámetros ![]() *R(r)
y paralelamente se construyen gráficos de todo ello. Estos resultados
se reflejan como un trazo ridge (trazo de cresta) en el cual las estimaciones
de los coeficientes para predictores colineales cambian muy rápidamente
a medida que K va aumentando desde cero, pudiendo incluso variar de signo. Los
cambios de signo y de magnitud, que al principio son muy bruscos, pronto se
estabilizan y van variando muy lentamente. Los estimadores de los coeficientes
de variables no colineales no cambian tan bruscamente, sino que lo hacen gradualmente
desde el principio, a medida que K aumenta. Cuando los estimadores de los coeficientes
para las variables colineales se estabilizan y empiezan a cambiar gradualmente
de la misma forma que lo hacen los estimadores de las variables no colineales,
es el momento de seleccionar un valor de K.
*R(r)
y paralelamente se construyen gráficos de todo ello. Estos resultados
se reflejan como un trazo ridge (trazo de cresta) en el cual las estimaciones
de los coeficientes para predictores colineales cambian muy rápidamente
a medida que K va aumentando desde cero, pudiendo incluso variar de signo. Los
cambios de signo y de magnitud, que al principio son muy bruscos, pronto se
estabilizan y van variando muy lentamente. Los estimadores de los coeficientes
de variables no colineales no cambian tan bruscamente, sino que lo hacen gradualmente
desde el principio, a medida que K aumenta. Cuando los estimadores de los coeficientes
para las variables colineales se estabilizan y empiezan a cambiar gradualmente
de la misma forma que lo hacen los estimadores de las variables no colineales,
es el momento de seleccionar un valor de K.
Este tipo de regresión ridge se denomina como simple, ya que se elige un sólo K para todos los predictores. En la regresión ridge generalizada hay un valor de K para cada predictor. Parece ser que el error cuadrático medio tiende a ser menor en la regresión ridge simple y mayor en la generalizada (Cattin, 1981).
Un ejemplo del análisis de regresión ridge se presenta en López (1995b), donde se explican con detalle algunas salidas de paquetes estadísticos, resaltando las ventajas de la regresión ridge respecto a la regresión común y al procedimiento stepwise de selección de predictores.
Hemos dicho que la elección o no de esta regresión depende del valor de los coeficientes de la verdadera regresión, que son desconocidos. No obstante, existen dos métodos de diagnóstico para detectar colinealidad que se asocian a la regresión ridge. El primero está relacionado con el efecto que tiene la colinealidad sobre los errores entre los estimadores MCO y los verdaderos valores de los coeficientes de regresión. El segundo método se relaciona con la inestabilidad que muestran los estimadores MCO cuando se introducen pequeños cambios en los datos originales del análisis.
El primer método se asocia con la noción del
FIV (Factor de Incremento de Varianza). En este sentido, la precisión
de un coeficiente estimado por MCO se mide por su variación, que es proporcional
a σ2 o varianza del término residual en el modelo de
regresión. La constante de proporcionalidad es un Factor de Incremento
de Varianza (FIV), que se define como el elemento de la diagonal de la matriz
de correlaciones. Hay un FIV correspondiente a cada coeficiente MCO estimado.
El FIV para ![]() i
es igual a ( 1-R2 )-1 , donde R2i
es el cuadrado del coeficiente de correlación múltiple de la regresión
de la iésima variable explicativa sobre el resto de los predictores.
En la interpretación de estos factores, se puede considerar que para
un FIV superior a 10, la multicolinealidad que se está produciendo es
ya suficiente como para causar problemas en la estimación.
i
es igual a ( 1-R2 )-1 , donde R2i
es el cuadrado del coeficiente de correlación múltiple de la regresión
de la iésima variable explicativa sobre el resto de los predictores.
En la interpretación de estos factores, se puede considerar que para
un FIV superior a 10, la multicolinealidad que se está produciendo es
ya suficiente como para causar problemas en la estimación.
Los FIVs pueden utilizarse también para obtener la expresión del cuadrado de la distancia esperada entre los estimadores MCO y sus valores esperados. Esta distancia es en definitiva, otra medida de la precisión de los estimadores mínimo cuadráticos. Si el cuadrado de la distancia es L2 , tenemos:
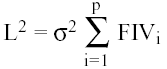 (24)
(24)
En el caso de que las variables explicativas sean ortogonales, los FIVs son todos igual a uno, y L2 tomará el valor ( ρσ2 ). De ello se sigue la siguiente razón:
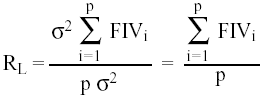 (25)
(25)
expresión que mide el error de los estimadores MCO para el caso en que los datos originales sean ortogonales, lo que en definitiva constituye también un índice de colinealidad.
Hacemos a continuación un breve repaso sobre la extensa literatura acerca de este análisis. Como muestra, sólo la revista Technometrics ha dedicado en el espacio de 12 años, 30 artículos a los conceptos de ‘parámetros sesgados o parciales’, o a la caracterización de la regresión ridge y a la discusión de su eficacia como una técnica de aplicación, entre otras cuestiones. También son varias las técnicas que se asocian a este tipo de regresión, como las expuestas en los artículos de Marquardt (1970); Mayer y Wilke (1973); Hocking, Speed y Lynn (1976) y Webster, Gunst y Mason (1974).
La regresión ridge es una estrategia ya vigente durante más de 30 años, desde el primer trabajo de Hoerl (1959) sobre el análisis ridge, revisado después por Hoerl (1985). En este último artículo, Hoerl manifesta las ‘tremendas ventajas’ del análisis ridge sobre el resto de los procedimientos de análisis de superficies de respuesta cuando hay mas de dos predictores. Sin embargo se queja de que no se le ha prestado suficiente atención y que quizá el análisis canónico, que se fue desarrollando también al mismo tiempo, ha cobrado una relevancia excesiva, generalizándose a las superficies de respuesta multidimensionales. Otra de las razones de este trato desfavorecedor de la regresión ridge encuentra su raíz en la confusión creada entre el análisis ridge y la regresión ridge. El primero se aplicaría, como hemos dicho, a una situación de superficies de respuesta de muchos predictores, y la regresión ridge sería un caso concreto del análisis ridge, donde aparecen relaciones colineales entre los predictores.
Por supuesto ha habido también numerosas críticas a la regresión ridge, cuestionando su validez, sobre todo en lo referente al uso abusivo de los diseños por simulación utilizados para demostrar su eficacia: Draper y Van Nostrand (1979); o bien sobre las bases mismas del procedimiento ridge como regresión parcial o sesgada: Smith y Campbell (1980); así como distintos comentarios del procedimiento del trazo ridge: Coniffe y Stone (1973) y (1975).
Hay también textos más próximos al ámbito de las Ciencias Humanas que tratan esta estrategia estadística: en Draper y Smith (1981: 313-349) se trabaja este procedimiento desde un planteamiento bayesiano, pasando por su forma canónica, y terminando con una aplicación bastante ilustrativa. Gunst y Mason (1980: 340-348) aplican el ANOVA a esta estrategia de regresión. Chatterjee y Price (1991: 185 y ss.) se detienen en el diagnóstico de la colinealidad apoyado en la regresión ridge. También los trabajos de Belsley et al. (1980), Belsley (1991), Weisberg (1985) y Seber (1977) tienen referencias interesantes. En Hocking (1976) se señala una lista completa de estudios sobre regresión ridge.
Por último, dentro del campo de la Psicología Aplicada apuntamos el crítico artículo de Darlington (1978) y el trabajo de Cattin (1981), donde se muestra un estudio por simulación que refleja el poder predictivo de la regresión ridge, así como un análisis comparativo en relación al tamaño muestral que debe tener la matriz de datos. Por otro lado, dado que la teoría que subyace en la regresión ridge se empezó a desarrollar para el caso de efectos fijos (Hoerl y Kennard, 1970), con el artículo de Darlington se extiende su estudio a la situación de efectos aleatorios, mucho más común en el campo de las Ciencias Humanas.
Las aplicaciones y extensiones de estos análisis se han dirigido sobre todo a los ámbitos de Ingeniería Química, Física Nuclear y Ciencias Económicas. Desde la esfera de los estudios de la Conducta o la Investigación Educativa de nuestro país no se tiene gran conocimiento de ello; hay alguna aplicación en el tema de selección de personal (Darlington, 1978). No hemos encontrado apenas ningún texto en castellano que trate estos análisis. Unicamente en Peña (1987: 417) se mencionan, refiriéndose a la regresión ridge como regresión contraída. No obstante, debido a que constituye uno de los mejores tratamientos de la colinealidad, y dado que nuestro marco de investigación es ciertamente delicado desde la naturaleza misma de nuestras variables, por no entrar en las relaciones tan particulares y variadas que entre ellas se generan, cabe pensar que la colinealidad en las regresiones de trabajos que estudian la conducta o fenómenos educativos lamentablemente resulta ser un problema harto frecuente. Por ello es clara la necesidad de un estudio detallado, monográfico, de la regresión ridge, como de tantos otros temas relacionados con el modelo de regresión, que vayan aproximando estos procedimientos a nuestros ámbitos, y dejen de ser análisis ajenos y desconocidos. El trabajo desarrollado en López (1992) intenta responder a esta inquietud.
Un ejemplo
En López (1998), se presenta un caso donde se localiza un claro problema de colinealidad entre los predictores del modelo original, tratando en esa ocasión distintos procedimientos para su diagnóstico. Aquí retomamos el mismo ejemplo y corregimos las consecuencias de las relaciones multicolineales que aparecen, utilizando una Regresión de Componentes Principales (RCP). Se trata de explicar la variación de la variable «Rendimiento en Matemáticas» (RDMAT) por medio de tres variables independientes: «Aptitud Numérica» (APTNUM); «Razonamiento Lógico» (RAZONA) y «Madurez Intelectual» (MADINTE), en una muestra de 76 sujetos. El análisis se realiza fácilmente con el programa 4R del paquete estadístico BMDP. La salida que resulta aparece a continuación en la Tabla 1.
En primer término obtenemos la matriz de correlaciones que muestra cómo los predictores iniciales se encuentran altamente correlacionados con el criterio (RDMAT), lo cual es eficaz para la explicación de esta variable; sin embargo, tanto la «Aptitud Numérica», como el «Razonamiento Lógico» y la «Madurez Intelectual» están fuertemente relacionados por medio de combinaciones lineales. El mismo diagnóstico de colinealidad se ve reforzado por los eigenvalores próximos a cero.
Con la salida hemos obtenido los cálculos necesarios para construir el modelo de regresión de componentes principales. Así, por ejemplo, teniendo en cuenta los eigenvectores, los componentes quedan expresados según las puntuaciones típicas de las variables independientes originales y construyen el modelo (8) (*1):
CP1 = 0.6087 Z1 + 0.5507 Z2 + 0.5711 Z3
CP2 = - 0.1067 Z1 + 0.7701 Z2 - 0.6289 Z3
CP3 = - 0.7862 Z1 + 0.3219 Z2 + 0.5279 Z3
Las correlaciones de cada componente con el Rendimiento en Matemáticas son (*2):
rCP1,Y = 0.84983, r CP2,Y = - 0.22770 y rCP3,Y = 0.09579
La salida también aporta los coeficientes de regresión de los componentes, lo que permite construir el modelo RCP (13) (*3):
Y = 19.16447 + 3.60499 CP1i - 2.35459 CP2i - 1.66594 CP3i
Dado que los componentes principales son mutuamente ortogonales, estos coeficientes no dependen del orden de entrada de los componentes en la ecuación, lo que no sucede en la regresión común de mínimos cuadrados ordinarios (MCO). De esta forma se han definido tres dimensiones subyacentes en los predictores originales, los nuevos componentes, lo que ha supuesto una rotación de los ejes originales que conformaban los predictores a unos nuevos ejes, ortogonales entre sí, y que maximizan sucesivamente la varianza de la proyección de la nube de puntos sobre ellos.
Los CPj se calculan posteriormente para cada uno de los sujetos, es decir, el programa multiplica los coeficientes de cada componente por los valores estandarizados de los predictores para cada sujeto: proyectando el vector que representa a cada sujeto sobre los nuevos ejes, se obtienen las puntuaciones de los 76 sujetos en los componentes generados.
Por último, el programa construye una tabla de resultados con la siguiente información (*4):
- el componente que entra en cada paso;
- la suma de cuadrados residual de cada paso: Σ (y i - y^i )2 , donde y ^ es el valor pronosticado;
- el estadístico F para el modelo de regresión: media cuadrática de regresión / media cuadrática residual. Los grados de libertad en este caso son son p y N-p-1, donde p es el número de componentes generados. Esto es el test de significación de la ecuación de regresión (13);
- el valor F de entrada: es el test de significación del coeficientes de cada componente; los grados de libertad para estos valores F son 1 y N-p-1;
- la correlación múltiple cuadrada;
- la constante y los coeficientes de los predictores originales correspondientes a los componentes que entran en cada paso.
Podemos comparar la regresión de componentes principales (RCP) realizada con el programa 4R del paquete estadístico BMDP, donde detallamos los resultados cuando se han introducido uno, dos o tres componentes, y las regresiones que se obtienen por medio de mínimos cuadrados ordinarios (MCO), por el procedimiento stepwise de selección de predictores, o por el procedimiento del «mejor subgrupo» (MS), ejecutados con los programas 1R, 2R y 9R respectivamente. Los coeficientes de regresión, así como las correlaciones cuadradas obtenidas en cada modelo, se muestran en la Tabla 2:
Si observamos los coeficientes de regresión y las correlaciones R2 de la regresión RCP cuando ya se han introducido los tres componentes, resultan ser los mismos que en la regresión común (MCO), pero con la seguridad de que ahora no se han utilizado predictores redundantes en la explicación del criterio. Del mismo modo, la proporción de varianza del Rendimiento en Matemáticas explicada por estos componentes (el coeficiente de determinación R2 ) resulta muy similar a los demás modelos de regresión que no corrigen la colinealidad, MCO o MS, lo que indica que en la regresión con componentes principales no se pierde eficacia en el poder predictivo del modelo de regresión: el uso de componentes principales iguala la explicación del criterio realizada en MCO (78.32%) y la supera en en el caso de la regresión stepwise (78.32% > 78.19%) y de la regresión por medio del mejor subgrupo (78.32% > 72.75%, 78.19%, 72.97%, 71.08%).
En la regresión stepwise, de los tres predictores originales sólo se ha podido trabajar con dos: para explicar el «Rendimiento en Matemáticas» el programa no permite utilizar la información aportada por el «Razonamiento Lógico», dado que esta variable resulta redundante con el predictor que ya se encuentra en el modelo, la «Aptitud numérica». Sin embargo, en la regresión RCP no se pierde información de ningún predictor a causa de las relaciones colineales que presentan, luego las tres variables explicativas no sólo contribuyen a explicar la variación del «Rendimiento en Matemáticas», sino que las relaciones que mantienen entre ellas son aprovechadas precisamente para este mismo fin.
En la regresión que busca el mejor subgrupo de predictores (MS), se presentan resultados para la selección de una variable independiente (APTNUM), o de los subgrupos compuestos por las parejas de predictores. De estos análisis, el mejor subgrupo resulta ser la regresión donde intervienen como predictores la «Aptitud Numérica» y la «Madurez Intelectual» (igual que sucede con stepwise). Las ventajas de la regresión RCP sobre el procedimiento MS son las mismas que las referidas anteriormente a la regresión stepwise.
Todas estas cuestiones a las que nos hemos venido referiendo justifican sobre manera el uso de la Regresión con Componentes Principales cuando se realizan regresiones con predictores colineales, y además convierten este análisis, junto con la Regresión Ridge, en la estrategia más indicada cuando precisamente lo que interesa es aprovechar las fuertes relaciones entre los predictores para la explicación de un fenómeno.
Batista, J. M. y Martínez, R. (1989). Análisis multivariante. Análisis de Componentes principales. Barcelona: Hispano Europea.
Belsley, D. A. (1991). Conditioning diagnostics. New York: Wiley.
Belsley, D. A.; Kuh, E. y Welsch, R. E. (1980). Regression diagnostics.New York: Wiley.
Cattin, P. H. (1981). The Predictive Power of Ridge Regression. Some Quasi-Simulation Results. Journal of Applied Psychology, 66, 3, 282-290.
Cliff, N. (1988). The eigenvalues-greater-than-one rule and the reability of components. Psychological Bulletin, 103, 2, 276-279.
Coniffe, D. y Stone, J. (1973). A critical view of ridge regression. The Statistician, 22, 181-187.
Coniffe, D. y Stone, J. (1975). A reply to Smith and Goldstein. The Statistician, 24, 67-68.
Chatterjje, S. y Price, B. (1991). Regression analysis by example. 2nd Ed. New York: Wiley.
Darlington, R. B. (1978). Reduced-Variance Regression. Psychological Bulletin, 85, 6, 1238-1255.
Draper y Smith, H. (1981). Applied regression analysis. New York: Ed. John Wiley.
Draper, N. R. y Van Nostrand, R. C. (1979). Ridge Regression and James-Stein Estimation: Review and Comments. Technometrics, 21, 451-466.
Green, B. F. (Jr). (1977). Parameter sensitivity in multivariate methods. Journal of Multivariate Behavioral Research, 12, 263-287.
Gunst, R.T. y Mason, R. L. (1980). Regression analysis and its application. New York: Marcel Dekker.
Harris, R. J. (1985). A primer of Multivariate Statistic. London: Academic Press.
Hocking, R. R. (1976). The analysis and selection of variables in linear regression. Biometrics, 32, 1-49.
Hocking, R. R., Speed, F.M. y Lynn, M. J. (1976). A class of biased estimators in linear regression. Technometrics, 18, 425-438.
Hoerl, A. E. (1959). Optimum solution of many variables equations. Chemical Engineering Progress, 55, 69-78.
Hoerl, A. E. (1964). Ridge Analysis. Chemical Engineering Progress, Symposium Series. 60, 67-77.
Hoerl, A. E. y Kennard, R. W. (1970). Ridge Regression: Biased Estimation for nonorthogonal Problems. Technometrics, 12, 1, 55-67.
Hoerl, R. W. (1985). Ridge Analysis 25 Years Later. American Statistician, 39. 3, 186-192.
López, E. (1992). La Regresión Multiple aplicada a la Investigación Educativa. Algunas consideraciones en torno a su correcta aplicación. Málaga: Universidad de Málaga.
López, E. (1995a). Regresión con Componentes Principales aplicada a predictores colineales. En AIDIPE (Comp.) Estudios de investigación educativa en intervención psicopedagógica (pp. 3-6). Valencia: Asociación Interuniversitaria de Investigación Pedagógica Experimetal.
López, E. (1995b). Regresión Ridge: un procedimiento para corregir la colinealidad entre predictores. En AIDIPE (Comp.) Estudios de investigación educativa en intervención psicopedagógica (pp. 44-50). Valencia: Asociación Interuniversitaria de Investigación Pedagógica Experimetal.
López, E. (En preparación). Colinealidad en Regresión Múltiple: diagnóstico.
Lovie, P. y Lovie, A. D. (Eds.) (1991). New Developments in Statistics for Psychology and the Social Sciences. Vol. 2. London: The British Psychological Society.
Marquardt, D. W (1970). Generalized inverses, ridge regression and biased linear estimation. Technometrics, 12, 591-612.
Marquardt, D. W. y Snee, R. D. (1975). Ridge Regression in Practice. American Statistician, 29, 1, 3-20.
Mauro, R. (1990). Understanding L.O.V.E. (Left Out Variables Error): A Method for Omited Variables. Psychological Bulletin,108, 2, 314-329.
Mayer, L. S. y Wilke, T. A. (1973). On biased estimation in linear models. Technometrics, 15, 497-508.
McCallum, B. T. (1970). Artificial Orthogonalization in Regression Analysis. Review of Economics and Statistics, 52, 110-113.
Mosteller, F. y Tukey, J. W. (1977). Data Analysis and Regression. (A second course in statistics). London: Addison-Welsley.
Peña, D. (1987). Estadística. Modelos y Métodos.Vol. 2: Modelos lineales y series temporales. Madrid: Alianza.
Riba, M. D. (1989). Una panorámica de las técnicas estadísticas multivariantes. Doc. de laboratori de Psicología Matemática. Barcelona: Univ. Autónoma.
Seber, G. A. F. (1977). Linear Regression Analysis. New York: Wiley.
Smith, G. y Campbell, F. (1980). A critique of some regression methods. Journal of the American Statistical Association, 75, 74-81.
Stein, C. (1960). Multiple regression. En Olkin, I. et al. (Eds.) Contribution to probability and statistics. Stanford, Calif.: Stanford University Press.
Stone, M. y Brooks, R. J. (1990). Continium Regression: Cross-validated sequentially constructed prediction embracing ordinary least, partial least squares y principal components regression. Journal Royal Statistical Society, Ser. B. 52, 2, 237-269.
Webster, J. T.; Gunst, R. F. y Mason, R. L. (1974). Latent root regression analysis. Technometrics, 16, 513-522.
Weisberg, S. (1985). Applied linear regression. New York: Wiley.
Aceptado el 22 de enero de 1998