Psicothema, 1998. Vol. Vol. 10 (nº 3). 623-631

Isabel Cañadas Osinski y Alfonso Sánchez Bruno

Universidad de La Laguna

Se estudiaron los cuantificadores lingüísticos de frecuencia empleados en las escalas de categorías. El objetivo último es lograr listados de cuantificadores consistentes, que garanticen el buen uso de las técnicas paramétricas. El trabajo consta de dos partes: la primera nos ha permitido fijar un listado previo de cuantificadores consistentes a través del método de estimación de magnitud, así como evaluar las posibilidades de uso de este procedimiento; en la segunda, generalizamos los resultados obtenidos en la primera fase ampliando el estudio a diferentes comunidades autónomas españolas.

Response categories in Likert-scale. Linguistic quantifiers of frequency which are employed in category scales were studied. Our final aim is to achieve consistent lists of quantifiers, which may warrant a proper use of the parametric techniques. This paper consists of two parts: the former has allowed us to set a previous list of consistent quantifiers by using the magnitude estimation method and to make an assessment of the possibilities of use of this procedure; in the latter part the results obtained in the first part are generalized so that a wider research could be made in other Spanish communities.

Con toda probabilidad, la escala de categorías constituye una de las técnicas de medida de creencias, preferencias y actitudes más utilizada por los científicos de la conducta. En palabras de Dawes (1975), se trata de «la omnipresente escala de clasificación» (pág. 115). Son muchos los términos asociados a la escala de categorías: escala de clasificación, escala de juicio absoluto, escala cerrada, escala de valoración resumida, escala de múltiple elección, escala tipo Likert, etc. En cualquier caso, bajo todas estas denominaciones se hace referencia a un procedimiento de escalamiento en el que el sujeto asigna los estímulos a un conjunto específico de categorías o cuantificadores lingüísticos, en su mayoría, de frecuencia (siempre, a veces, nunca, etc,) o de cantidad (todo, algo, nada, etc.).

La escala de categorías se utiliza con gran profusión, tanto en la psicología aplicada como en otros ámbitos (estudios de opinión, marketing, etc.), ya que la verbalización forzada que supone responder conforme a este formato conlleva una serie de ventajas, entre las que destacamos: menor ambigüedad de respuestas que las obtenidas con otro tipo de cuestionarios, mayor cercanía de las respuestas al objetivo del investigador, permiten recabar más información en menos tiempo, etc. En suma, se puede considerar que la escala de categorías es relativamente barata y fácil de desarrollar para el investigador y sencilla de comprender y rápida de contestar para el sujeto. Como afirman González, Lameiras y Varela (1990), «su capacidad para estimar la intensidad de la impresión de la forma más sencilla posible para el encuestado es difícilmente sustituible» (pág. 411).

Sin embargo, este procedimiento de escalamiento también presenta algunos inconvenientes que conviene no olvidar. En primer lugar, la presunción de invariabilidad y estabilidad de significado de los cuantificadores lingüísticos. En este contexto, la investigación se ha centrado en el estudio correspondiente a la influencia de factores tales como la ubicación de los cuantificadores, el contexto dentro del cual los sujetos realizan las evaluaciones (Cañadas, 1992), el emparejamiento con adverbios, las diferencias individuales, formatos de respuestas, etc. y, si bien la investigación ha sido amplia, no ha resultado concluyente. En segundo lugar, y desde nuestro punto de vista el problema más importante, la cuestión relativa al nivel de medida alcanzado por la escala de respuestas. En este sentido, señala Spector (1976) que el criterio de selección de los cuantificadores se realiza sobre bases no más sólidas que el hábito o la imitación asumiéndose que, además de estar ordenados por su intensidad, se ajustan a escalas de intervalos. Sin embargo, un gran número de autores afirma que se encuentran sólo a un nivel ordinal de medida (Hartley, Trueman y Rodgers, 1984; Lee Rasmussen, 1989; González, Lameiras y Varela, 1990; Meek, Sennot-Miller y Ferketich, 1992; Wills y Moore, 1994; Schriesheim y Castro, 1996, etc).

Bajo el supuesto de que tan solo se alcance el nivel ordinal encontramos el problema de que los datos derivados de tales respuestas no pueden ser sumados o promediados, como exige el análisis de ítems y, en consecuencia, el uso de técnicas paramétricas resultaría muy comprometido. La práctica habitual resuelve este problema asignando números enteros ordenados a los cuantificadores y tratándolos posteriormente como si de una escala de intervalos se tratase, lo cual no tiene suficientes bases lógicas y, en menor medida, matemáticas. Si ciertamente estos conjuntos no se ajustan a una medida de intervalos, como tradicionalmente se asume, parece absolutamente necesario desarrollar nuevos conjuntos de cuantificadores que sí alcancen dicho nivel de medida.

En el contexto de las investigaciones dirigidas a resolver esta cuestión, un procedimiento que ha resultado útil ha sido el método de estimación de magnitud, desarrollado por Stevens (1975). Básicamente, el procedimiento consiste en presentar al sujeto una serie de estímulos, en nuestro caso, categorías de respuesta o cuantificadores lingüísticos, con uno de ellos actuando como referente y al que el sujeto asigna un valor de su elección; a continuación se valoran los restantes estímulos estableciendo una relación de proporcionalidad respecto al estímulo referente.

En esta parcela de investigación hay que destacar el trabajo llevado a cabo por Schreisheim y colaboradores quienes, a lo largo de más de dos décadas investigando con cuantificadores de frecuencia, han demostrado la superioridad de este método frente a otros que también se han utilizado con el mismo fin (la comparación de pares bajo el caso III de Thurstone o el método de rango normalizado) lo que les lleva a recomendarlo como el más idóneo para este tipo de estudios (Schriesheim y Schriesheim, 1974, 1978; Schriesheim y Novelli, 1989; Schriesheim y Gardiner, 1992; Schriesheim, Cogliser, Newmark y Lowenson, 1994 y Schriesheim y Castro, 1996).

Del mismo modo que han hecho Schreisheim y otros investigadores dentro de la lengua inglesa, nosotros nos hemos planteado la obtención de una relación estable de cuantificadores lingüísticos de frecuencia dentro de la lengua castellana, empleando el mismo procedimiento que estos autores, es decir, el método de estimación de magnitud. El objetivo último que perseguimos es la obtención de cuantificadores que alcancen un nivel de medida de intervalos que nos permita la utilización de procedimientos estadísticos paramétricos.

Estudio 1

El propósito de este primer estudio fue obtener los equivalentes numéricos de un conjunto de expresiones lingüísticas de frecuencia mediante el método de estimación de magnitud y, además, estudiar la estabilidad de tales expresiones lingüísticas.

En primer lugar, se pidió a los sujetos que asignaran un número de su elección a lo que ellos consideraban que significaba la expresión a veces. A continuación, y usando a veces como referente, se les pedía que asignaran a cada una de las restantes expresiones de frecuencia el número que reflejara mejor su valor relativo con respecto al referente a veces.

En segundo lugar, siguiendo las sugerencias de Stevens (1975), procedimos del mismo modo que Garner y Creelman (1976), Fucci, Petrosino y Harris (1985) y Kemp (1988) para comprobar la consistencia de los resultados obtenidos. A tales efectos, aplicamos la misma escala de expresiones lingüísticas, utilizando en este momento normalmente como estímulo de referencia, en lugar de a veces.

Se emplearon 19 expresiones de frecuencia, que fueron obtenidas en estudios previos (Cañadas, 1997), en una secuencia aleatoria. Para controlar los efectos del orden, aproximadamente la mitad de los sujetos siguió la secuencia en orden directo y el resto en orden inverso.

La muestra empleada para la obtención de los equivalentes numéricos estuvo formada por 104 estudiantes de ambos sexos de la Facultad de Psicología de la Universidad de La Laguna. Para el estudio de la consistencia se utilizó otra muestra constituida por 137 estudiantes de ambos sexos de 1º y 2º curso de la Facultad de Psicología de la Universidad de La Laguna.

El procedimiento habitual para obtener los valores numéricos de las expresiones lingüísticas es el cálculo de la media geométrica de las estimaciones de los sujetos correspondientes a cada cuantificador. Este índice presenta la ventaja de no requerir la transformación a un módulo común de las estimaciones –téngase en cuenta que cada sujeto parte de un valor numérico de su elección– y, además, las distribuciones de las estimaciones se tornan más simétricas (Stevens, 1975).

Sin embargo, antes de proceder al cálculo de las medias geométricas, a fin de incluir las estimaciones iguales a cero, se sumó a cada puntuación una cantidad fija de 0,01 y se calculó el logaritmo del valor resultante; a continuación, se obtuvo la media aritmética de los logaritmos correspondientes a cada cuantificador y se transformó este resultado en su antilogaritmo; la media geométrica se obtuvo restando a cada uno de estos antilogaritmos la misma cantidad de 0,01; finalmente, se tomó como media de los logaritmos precisamente el logaritmo de esta media geométrica.

Para analizar la convergencia de resultados obtenidos con ambas muestras, se procedió al cálculo de los coeficientes de correlación de Pearson entre las medias geométricas obtenidas con los distintos referentes. Dado el alto grado de convergencia obtenido (r = 0,9966, p < 0,01), se procedió a un estudio pormenorizado de cada pareja de cuantificadores, correspondientes a los distintos referentes, con la finalidad de detectar posibles diferencias significativas entre ellos. Para ello, se utilizó un contraste t de Student para las medias de cada par de cuantificadores.

Conviene destacar en este punto que, antes de llevar a cabo los contrastes de medias, se realizó una transformación de las mismas a fin de hacerlas directamente comparables. A tales efectos, hemos seguido el procedimiento de igualación de extremos sugerido por Guildford (1954), que ha sido utilizado en diversos estudios de convergencia con estimación de magnitud (Schriesheim y cols., 1978, 1992 y 1996; Pohl, 1981). Este procedimiento se basa en la resolución del siguiente sistema de ecuaciones:

Xmin₁ = a + bXmin₂

donde Xmin₁ = puntuación mínima del grupo 1

Xmin₂ = puntuación mínima del grupo 2

Xmax₁ = puntuación máxima del grupo 1

Xmax₂ = puntuación máxima del grupo 2.

De esta forma, las puntuaciones del grupo 2 fueron transformadas aplicando los coeficientes a y b así obtenidos de modo que los valores extremos de ambos grupos quedaron igualados y no fueron, por tanto, incluidos en los contrastes.

La penúltima columna de la Tabla 1 nos ofrece los valores de t en los contrastes de las medias transformadas. Como se puede observar, no hubo ninguna diferencia estadísticamente significativa en las expresiones.

Las altas correlaciones obtenidas entre los conjuntos de cuantificadores, así como la falta de diferencias significativas entre cada par, nos permiten obtener una relación única de expresiones de frecuencia, como se muestra en la última columna de la Tabla 1. Las medias geométricas, obtenidas a partir de los antilogaritmos de las medias aritméticas de los logaritmos, representan los valores numéricos para las escalas conjuntas de cuantificadores propuestas.

La lista aquí presentada nos permite ofrecer recomendaciones relativas a los puntos de anclaje cuya escala subyacente sea de intervalos. El procedimiento para construir escalas intervalares consiste, simplemente, en lo siguiente: dados los valores mínimo y máximo de la escala y el número de categorías a utilizar, los valores de anclaje necesarios para establecer una escala con distancias iguales se calculan mediante la expresión:

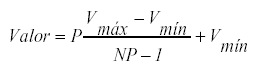
donde P es la categoría considerada, V _max y V_min son los valores máximo y mínimo de la escala, respectivamente, y NP es el número de categorías de la escala.

De esta forma, y a modo de ejemplo, si quisiéramos construir una escala de intervalos con cinco categorías de frecuencia, aplicando la expresión anterior nos encontramos con las siguientes expresiones: nunca, a veces, generalmente, muchísimas veces y siempre.

En definitiva, podemos decir que los resultados obtenidos son estables dentro del ámbito estudiado. Sin embargo, no resulta aconsejable ofrecer una lista de cuantificadores válidos, al menos para la población española, desde una visión tan localista (este estudio se ha llevado a cabo en la Universidad de La Laguna). Esta consideración nos llevó a realizar el Estudio 2.

Estudio 2

A la vista de los resultados obtenidos en el estudio anterior y a fin de generalizar y validar la lista de cuantificadores lingüísticos obtenida, en esta fase de la investigación nos planteamos la aplicación de los cuestionarios utilizados en el Estudio 1 en diversas comunidades españolas, con la finalidad de presentar una única lista unificada de cuantificadores de frecuencia, que podría ser utilizada a la hora de elaborar escalas psicológicas de lengua castellana y cumplimentar así el objetivo último de la investigación.

Para llevar a cabo este estudio, se aplicó el mismo procedimiento empleado en el Estudio 1 a cada una de las comunidades autónomas de Cataluña, Andalucía, Madrid y Galicia y se realizaron los mismos análisis estadísticos.

Las muestras empleadas en este estudio fueron estudiantes de ambos sexos de 1º y 2º curso de las Facultades de Psicología de las siguientes Universidades: 186 de la Universidad Central de Barcelona, 197 de la Universidad Complutense de Madrid, 194 de la Universidad de Santiago de Compostela y 188 de la Universidad de Granada.

Dentro de cada una de las comunidades estudiadas nos hemos encontrado con resultados tan estables como los del Estudio 1 (que corresponde al grupo de Tenerife). Esta consistencia ha sido avalada tanto por los elevados coeficientes de correlación encontrados, como por la ausencia casi total de diferencias significativas entre pares de cuantificadores (sólo las expresiones raramente en Barcelona y a veces en Granada resultaron estadísticamente distintas).

De este modo, pasamos a la segunda parte de este estudio que se enfocó hacia la comparación de los resultados obtenidos con todos los grupos. Para facilitar esta tarea, y como paso previo al análisis estadístico, se representaron las escalas conjuntas comparables de cada grupo (Figura 1). Como se puede apreciar, el grupo de Tenerife difiere bastante en sus estimaciones del resto de los grupos.

Este hecho se ve confirmado por los resultados obtenidos en los análisis de varianza. En este sentido, para la comparación de las medias obtenidas en los cinco grupos, se llevó a cabo un ANOVA de un factor (el grupo) con cinco niveles (cada uno de los lugares donde se obtuvieron las estimaciones) para cada cuantificador. Además, los valores F estadísticamente significativos vienen acompañados de los resultados obtenidos con las pruebas a posteriori utilizando el método de Scheffé.

Como se puede ver en la Tabla 2, seis cuantificadores de frecuencia (normalmente, a veces, algunas veces, de vez en cuando, alguna vez y casi nunca) resultaron estadísticamente distintos, siendo Tenerife el factor común en todas estas diferencias (este hecho quedó además corroborado al realizar de nuevo los mismos análisis excluyendo Tenerife, donde las divergencias observadas anteriormente desaparecieron por completo).

Para poder encontrar una explicación a estos resultados procedimos a una inspección más detallada de las puntuaciones otorgadas por los sujetos a los cuantificadores. Nos llamó la atención encontrar que el grupo de Tenerife puntuó en menor proporción con valores cero al cuantificador nunca. Esta gran diferencia en el porcentaje de respuestas cero observada entre Tenerife y los grupos de la Península (Tenerife: 79,1 y Península: 92,0) afecta sustancialmente a los resultados debido a que la necesaria igualación previa a la comparación entre los grupos hace uso precisamente del valor arrojado por este cuantificador. En la medida en que existan distancias desiguales entre el valor asignado a nunca y los asignados a las expresiones inmediatamente superiores, el proceso de igualación tenderá a amplificar las separaciones intergrupo correspondientes a este cuantificador.

Dado que los patrones de respuesta fueron similares en todos los lugares, salvo en lo que al cuantificador nunca se refiere, todo apunta a que las diferencias encontradas entre el grupo de Tenerife y los demás pueden deberse o bien a un efecto de las instrucciones, que puede derivar en un efecto del experimentador (nótese que en Tenerife son los autores del trabajo los que llevaron a cabo la aplicación del procedimiento), o bien al significado conceptual del cuantificador nunca para los sujetos, o bien a ambos a la vez.

Otra explicación plausible se corresponde con la transposición del método de estimación de magnitud que se hace en estudios como el que aquí presentamos. Nótese que el método aplicado a estímulos físicos, tal y como se hace tradicionalmente, no trae consigo mayor problema puesto que por muy pequeña que sea la estimulación, siempre se presenta en alguna cantidad. Sin embargo, con estímulos como los aquí estudiados, el cuantificador nunca sí puede conllevar ausencia de magnitud. En cualquier caso, en esta investigación, no podemos dar respuesta a estos interrogantes.

Conclusiones

Pese a las limitaciones anteriormente expresadas, sobre la base de nuestros resultados, se puede decir que los cuantificadores de frecuencia del castellano empleados en este trabajo presentan un alto grado de estabilidad, lo que permite elaborar una única lista para su uso en la investigación aplicada. Además, el procedimiento aquí empleado garantiza el nivel de medida de intervalos de los cuantificadores propuestos y, en consecuencia, el buen uso de las técnicas paramétricas.

Para finalizar, presentamos ejemplos de escalas de cuantificadores intervalares. Dado que, como ya señalamos anteriormente, las diferencias encontradas entre Tenerife y el resto de los lugares estudiados se deben al cuantificador nunca, para poder incluir a este grupo, la escala que proponemos (Tabla 3) excluye este cuantificador. Hay que señalar que los cuantificadores que se sugieren para la escala fueron sometidos previamente a un análisis de varianza excluyendo el cuantificador nunca, según ya hemos comentado, que no arrojó diferencias significativas.

Cañadas, I., Prieto, P., San Luis, C. y Domínguez, F. (1992). Estudio de cuantificadores lingüísticos de frecuencia y de cantidad al uso en escalas psicológicas españolas. III Simposium de Metodología de las CC. Sociales y del Comportamiento. Santiago de Compostela.

Cañadas Osinski, I. (1997). Estudio de cuantificadores lingüísticos y su aplicación en escalas psicológicas. Tesis doctoral. Universidad de La Laguna.

Dawes, R.M. (1975). Fundamentos y técnicas de medición de actitudes. México: Limusa.

Fucci, D., Petrosino, L. y Harris, D. (1985). A magnitude estimation response pool for production of lingual vibrotactile magnitudes. Perceptual and Motor Skills, 60, 763-766.

Garner, W.R. y Creelman, C.D. (1976). Problemas y métodos de la elaboración de escalas psicológicas. En G.F. Summers (Ed.) Medición de las actitudes. México: Trillas. 59-102.

González Lorenzo, M., Lameiras Fernández, M. y Varela Lovelle, M. (1990a). Escalamiento de magnitud en la satisfacción laboral I. Validez de la ley de potencia. Revista de Psicología General y Aplicada, 43(3), 411-417.

Guildford, J.P. (1954). Psychometric Method. New York: McGraw-Hill.

Hartley, J., Trueman, M. y Rodgers, A. (1984). The effects of verbal and numerical quantifiers on questionnaire responses. Applied Ergonomics, 15(2), 149-155.

Kemp, S. (1988). Magnitude estimation of the utility of nonmonetary items. Bulletin of the Psychonomic Society, 26(6), 544-547.

Lee Rasmussen, J. (1989). Analysis of Likert-scale data: A reinterpretation of Gregorire and Driver. Psychological Bulletin, 105, 167-170.

Meek, P., Sennott-Miller, L. y Ferketich, S. (1992). Scaling stimuli with magnitude estimation. Research in Nursing & Health, 15, 77-81.

Pohl, N.F. (1981). Scale considerations in using vague quantifiers. Journal of Experimental Education, 49, 235-240.

Schriesheim, C. y Castro, S. (1996). Referent effects in the magnitude estimation scaling of frecuency expressions for response anchor sets: an empirical investigation. Educational and Psychological Measurement, 56, 557-569.

Schriesheim, C., Cogliser, C.C., Newmark, R.I. y Lowensohn, S.H. (1994). The equal-interval nature investigation using fiedler´s least preferred coworked (LPC) scale and magnitude estimation and case III scaling procedures. Educational and Psychological Measurement, 54, 253-262.

Schriesheim, C. y Gardiner, G. (1992). A comparative test of magnitude estimation and pair-comparison treatment of complete ranks for scaling a small number of equal-interval frecuency response anchors. Educational and Psychological Measurement, 52, 867-877.

Schriesheim, C. y Novelli, J.R. (1989). A comparative test of the interval-scale properties of magnitude estimation and case III scaling and recommendations for equal-interval frecuency response anchors. Educational and Psychological Measurement, 49, 59-73.

Schriesheim, C. y Schriesheim, J. (1974). Development and empirical verification of new response categories to increase the validity of multiple response alternative questionnaires. Educational and Psychological Measurement, 34, 877-884.

Schriesheim, C. y Schriesheim, J. (1978). The invariance of anchor points obtained by magnitude estimation and pair-comparison treatment of complete ranks scaling procedures: an empirical comparison and implications for validity of measurement. Educational and Psychological Measurement, 38, 977-983.

Stevens, S.S. (1975). Psychophysics. New York: John Wiley & Sons.

Wills, C.E. y Moore, C.F. (1994). A controversy in scaling of subjetive states: Magnitude estimation versus category rating methods. Research in Nursing & Health, 17, 231-237.