Psicothema, 1998. Vol. Vol. 10 (nº 3). 717-724

Eduardo García-Cueto, Pedro Gallo Álvaro y Rubén Miranda

Universidad de Oviedo

Siguiendo el método de Montecarlo se ha llevado a cabo una simulación para el estudio del comportamiento de los índices de ajuste en el Análisis Factorial Confirmatorio. Se generaron 4.500 muestras con un total de 1.890.000 de sujetos bajo 45 condiciones distintas. Los resultados obtenidos muestran la dependencia de χ² del tamaño muestral, siendo prácticamente irrelevante el valor de las correlaciones intrafactoriales, mientras que los índices de Bentler y Bonett se ven afectados tanto por el tamaño muestral como por el valor de las correlaciones entre las variables que configuran una misma dimensión.

Confirmatory Factor Analysis goodness of fit. The most important Confirmatory Factor Analysis indices, (χ² , Bentler and Bonett) were studied, using Montecarlo methodology. 4500 samples were generated, under 45 different conditions. The results show that χ² adjustment index is influenced by sample size. The effect of intrafactor correlations was not statistically significant. Bentler and Bonett indices resulted affected by sample size, and by the correlations between those variables conforming the same factor. Theorical and practical implications of the results are discussed.

Hoy resulta superfluo el incidir sobre el uso del ordenador en la investigación en Psicología, así como reseñar el uso del análisis factorial como técnica en una gran cantidad de investigaciones de todo tipo. El acceso masivo a la informática y la facilidad de manejo de los programas de análisis de datos ha modificado, de forma decisiva, tanto la forma como el fondo de las investigaciones en todas las ciencias y la psicología no ha sido ajena a dicha transformación.

En la práctica totalidad de los modelos de medida utilizados en el ámbito de lo psicológico se hace mención expresa sobre la presunción de la dimensionalidad de las variables con las que se está trabajando: desde la Teoría Clásica de los Tests (Muñiz, 1998) hasta los últimos modelos de la Teoría de la Respuesta a los Ítems (van der Linden y Hambleton, 1997; Muñiz, 1998). En todos los casos, la técnica más aconsejada para el estudio de la dimensionalidad de las variables es el análisis factorial, ya sea el exploratorio o, con más precisión para el establecimiento y la comprobación de hipótesis, el análisis factorial confirmatorio (Hattie, 1985, Ferrando, 1996).

Por otro lado, para el establecimiento de comparaciones entre patrones de respuestas, en el estudio de la validez de constructo de los instrumentos de medida utilizados, para el estudio de la incidencia de las formas de recogida de información en todo lo que es medida en las ciencias sociales y de la salud, cada vez se acude con más frecuencia al análisis factorial como método y técnica para justificar la toma de decisiones y la generalización de los resultados obtenidos (Chico Librán, 1997; Tomás y Oliver, 1998).

Cuando se desean comparar estructuras factoriales y/o determinar el número de dimensiones subyacentes en cualquier matriz de datos se han propuesto diversos métodos (García-Cueto, 1994; Ferrando, Lorenzo y Chico, 1997); pero no cabe duda de la necesidad de acudir a procedimientos estadísticos cada vez más rigurosos (Muñiz, 1997) y los más adecuados pasan por el estudio confirmatorio de las estructuras factoriales.

Las limitaciones del modelo exploratorio están superadas por el desarrollo del modelo de análisis factorial confirmatorio. Resulta mucho más práctico disponer de un procedimiento de estimación que ofrezca garantías fuera de la propia subjetividad. En el modelo confirmatorio el investigador introduce, en palabras de Long, constreñimientos fuertemente fundados. De este modo se determina:

1.- Qué pares de factores comunes correlacionan.

2.- Qué factores comunes afectan a las variables observadas.

3.- Cuáles de las variables observables están afectadas por un factor único.

4.- Qué pares de factores únicos están correlacionados.

Se especifica en el modelo, además, la covarianza o la correlación entre las variables latentes. Se puede, de este modo, comprobar hasta qué punto los datos confirman el modelo generado de acuerdo a estos constreñimientos (Long, 1986).

Para el estudio de datos mediante este modelo de análisis factorial se han venido utilizando diversos programas de ordenador; principalmente el programa LISREL desarrollado por Jöreskog y Sörbom (1993) y el EQS ideado por Bentler. Ambos ofrecen, como principal índice de ajuste con el modelo, un estadístico que se distribuye aproximadamente como el estadístico χ². El programa EQS ofrece además otros dos índices: el índice de ajuste normado (Bentler y Bonett, 1980) que sitúa el ajuste de un determinado modelo en una escala desde el ajuste de línea base al ajuste perfecto. Éste sería el modelo más simple y restrictivo que se pueda aplicar a los datos (Loehlin, 1987) y el índice de ajuste no-normado, el cual responde a la necesidad de reducir la falta de control sobre los grados de libertad que afecta a la función del modelo ajustado en el índice normado (Martínez Arias, 1995). Ambos índices, uno más parsimonioso que otro, adolecen del mismo problema; carecen de distribución conocida, por lo que su interpretación es totalmente subjetiva. Se considera que cuanto más próximos están a 1 mejor es el ajuste. Su expresión matemática es la siguiente: (Indice de ajuste normado)

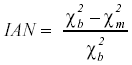
Donde χ_b² corresponde al estadístico del modelo de linea base y χ_m² es el estadístico correspondiente al modelo ajustado.

En cuanto al índice de ajuste no normado, su expresión matemática es la siguiente:

Siendo gl los grados de libertad correspondientes. Los demás símbolos tienen la misma interpretación que en la ecuación anterior.

El uso de χ² aporta la ventaja de permitir aceptar o rechazar una hipótesis a un nivel de confianza predeterminado, procedimiento habitual en la práctica totalidad de las investigaciones con las que el psicólogo está familiarizado.

En este contexto, con la presente investigación se pretende ver el funcionamiento de χ², como estadístico de contraste, bajo distintas condiciones, utilizando para ello datos simulados. Se intenta ver la influencia de las correlaciones entre las variables que han de configurar un mismo factor y el tamaño de la muestra sobre el comportamiento del citado estadístico.

Método

Para llevar a cabo la presente investigación se han manipulado las siguientes variables:

1.- Valor de la correlación entre las variables que iban a configurar cada factor, dando 10 valores desde 0.1 hasta 0.9

2.- Tamaño de la muestra (100, 200, 300, 500 y 1000 sujetos por grupo).

No se contemplaron valores muestrales inferiores a 100 sujetos, ya que no serían en absoluto adecuados para la realización de análisis factoriales, sobre todo en investigaciones en Psicometría, ni por encima de 1.000, teniendo en cuenta que su cuantía hace que no existan apenas diferencias entre la estimación muestral y los datos poblacionales. Todas las muestras siguen una distribución normal y la correlación entre las variables de distintos factores era de cero.

Se obtienen por lo tanto 45 condiciones, como resultado de cruzar la variable, valor de la correlación para cada tamaño muestral. Dentro de cada condición se llevaron a cabo 100 replicaciones con la finalidad de obtener resultados estables. Se generaron, pues, 4.500 muestras con un total de 1.890.000 de sujetos. El programa utilizado para la generación de datos fue desarrollado por el profesor Aguinis de la Universidad de Denver (Colorado). El programa está realizado en «Quick-Basic».

Las muestras de datos se analizaron mediante la subrutina de ecuaciones estructurales del programa estadístico EQS para Windows, creado por Bentler.

Se somete a prueba, mediante el estadístico χ² la siguientes hipótesis:

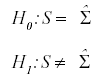
Siendo S la matriz de covarianzas observada y :

que define a la matriz de covarianzas estimadas.

Estos estadísticos siguen asintóticamente distribuciones de χ², distribuyéndose χ² con los siguientes grados de libertad: Número de parámetros independientes bajo la hipótesis alternativa, menos el número de parámetros independientes bajo la hipótesis nula:

g.l.= q (q+1) / 2- t

Siendo q el número de variables observadas y t el número de parámetros independientes asociados a H₀ que varían en función de cada modelo (Long, 1986).

Resultados

Los análisis factoriales confirmatorios llevados a cabo se realizan utilizando el método de máxima verosimilitud para la extracción de factores ortogonales. Las decisiones para aceptación o rechazo de la H₀ se hacen a un nivel de confianza del 95%.

La tabla 1 muestra los porcentajes de rechazo de la H₀ para cada una de las condiciones establecidas:

Como puede observarse el tanto por ciento de rechazos de la hipótesis nula parece estar en dependencia casi de forma exclusiva del tamaño de la muestra. χ² tiende a comportarse como se espera, en función del nivel de significación, a partir de tamaños muestrales por encima de 500 sujetos. Sim embargo, sorprendentemente, no parece verse afectado por el valor de las intercorrelaciones entre las variables.

A pesar de que los índices de Bentler y Bonett no tengan distribuciones conocidas, a continuación se muestran los valores mínimos de dichos índices que permiten aceptar la hipótesis nula, en función de χ².

Como puede observarse, los valores mínimos de los índices de Bentler y Bonett que permiten aceptar la hipótesis nula parecen en estrecha dependencia tanto del tamaño de la muestra como del valor de las intercorrelaciones entre las variables que configuran cada factor. Es necesario obtener índices cada vez más elevados cuanto mayores son los tamaños muestrales y cuanto mayor es la correlación entre las variables de una misma dimensión. Así, para una muestra de 100 sujetos, con un valor de la correlación entre las variables de 0,1, basta con un valor en los índices de 0,4 y 0,43 respectivamente, mientras que en la muestra de 1.000 sujetos con correlaciones de 0,9, el valor mínimo que permite no rechazar la hipótesis nula es de 0.977. Otra consideración que debe ser tenida en cuenta y que puede observarse tanto a través de la anterior tabla como de las gráficas siguientes es que es más exigente el índice no normado que el normado.

En las gráficas aquí expuestas puede observarse como los valores de las probabilidades asociadas con χ² aparecen como «paralelos» con los valores de los índices de Bentler y Bonett, siendo siempre y de forma sistemática mayores los valores obtenidos con el índice no normado. No se exponen todos los resultados obtenidos, ya que resultaría una lista interminable de gráficas que no añaden nada nuevo a lo que puede observarse a través de los datos aquí representados. Se exponen en la gráfica I y II el caso de 100 sujetos con correlación entre las variables que configuran un mismo factor de 0,1. En las gráficas III y IV, el caso de 500 sujetos con valores de 0,5 en las correlaciones y el caso de 200 sujetos con valores de 0,9 en las correlaciones entre las variables en las gráficas V y VI.

Discusión

La conclusión más obvia que parece desprenderse del presente trabajo es la dependencia de la prueba de bondad de ajuste de χ² del tamaño muestral; resultando paradójico, o al menos sorprendente, la poca incidencia que sobre la misma tiene el valor de las correlaciones entre las variables que configuran una misma dimensión. Una posible explicación a este hecho puede venir dada por la ortogonalidad entre los factores y la constancia de los valores de las correlaciones dentro de cada dimensión.

Es de sobra conocida por los investigadores la dificultad para que los datos empíricos reales se ajusten a una estructura factorial hipotetizada previamente; a pesar de que las correlaciones entre las variables que debían agruparse en un factor presenten entre sí valores correlacionales muy superiores a 0,1. La única explicación plausible puede ser, por un lado, la violación del supuesto de la ortogonalidad y, por otra parte, la variabilidad en las correlaciones entre las variables de la misma dimensión.

Esta investigación deja, pues, pendiente el estudio del comportamiento de χ² en el caso de la violación del supuesto de la ortogonalidad y cuando existe (como en la práctica es habitual) variabilidad en los valores de las correlaciones intrafactoriales.

Por otro lado, los índices (el normado y el no normado) de Bentler y Bonett parecen seguir comportamientos semejantes a los valores de la probabilidad asociada con χ², en el sentido siguiente, los valores altos de la probabilidad parecen ir parejos con altos valores de los índices, como se desprende del estudio visual de las gráficas aquí presentadas. Por otro lado la distancia entre los valores de ambos índices se reduce drásticamente en función, tanto del valor de las correlaciones entre las variables dentro de un mismo factor, como del tamaño muestral, es decir, resulta mucho más sensible a estas variaciones el índice normado que el no normado, lo que hace que con valores altos de las correlaciones intrafactores y con tamaños muestrales grandes los valores de ambos índices estén muy próximos, sin embargo al disminuir el valor de las correlaciones, el tamaño muestral o ambos, estos valores empiezan a distanciarse, resultando valores relativamente «muy bajos» para el índice normado incluso con probabilidades asociadas de χ² > 0,05.

Bentler, P. M. y Bonett, D. G. (1980) Significance tests and goodness of fit in the analysis of covariance structures. Psychological Bulletin, 88, 588-606.

Chico Librán, E. (1997) La invarianza en la estructura factorial del Raven en grupos de delincuentes y no delincuentes. Psicothema, 9(1), 47-55.

Ferrando, P. J. (1996) Evaluación de la unidimensionalidad de los ítems mediante análsis factorial. Psicothema, 8(2), 397- 410.

Ferrando, P. J., Lorenzo, U. y Chico, E. (1997) La técnica del análisis criterial: Algunas consideraciones y desarrollo de un programa informático. Psicothema, 9(3), 637-645.

García-Cueto, E. (1994) Coeficiente de congruencia. Psicothema, 6(3), 465-468.

Hattie, J. A. (1985) An empirical study of varius indices for determining unidimensionality. Multivariate Behavioral Research, 19, 49-78.

Jöreskog, K. G. y Sörbom, D. (1993) LISREL 8: Structural equation modeling with the Simplis command language. Hillsdale (NJ): Lawrence Erlbaum.

Long, J. S. (1986) Confirmatory factor analysis. Beverly Hills (CA): Sage.(orig. 1983)

Martinez Arias, M. R. (1995) Psicometría: Teoría de los tests psicológicos y educativos. Madrid: Síntesis.

Muñiz, J. (1997) Introducción a la teoría de respuesta a los ítems. Madrid: Pirámide.

Muñiz, J. (1998) La medición de lo psicológico. Psicothema, 10(1), 1-21.

Tomás, J. M. y Oliver, A. (1998) Efectos de formato de respuesta y método de estimación en el análisis factorial confirmatorio. Psicothema, 10(1), 197-208.

van der Linden, W. J. y Hambleton, R. K. (Eds.) (1997) Handbook of modern item response theory. Nueva York: Springer.