Psicothema was founded in Asturias (northern Spain) in 1989, and is published jointly by the Psychology Faculty of the University of Oviedo and the Psychological Association of the Principality of Asturias (Colegio Oficial de Psicología del Principado de Asturias).
We currently publish four issues per year, which accounts for some 100 articles annually. We admit work from both the basic and applied research fields, and from all areas of Psychology, all manuscripts being anonymously reviewed prior to publication.
Psicothema, 1991. Vol. Vol. 3 (nº 1). 199-218
M. Rosario MARTINEZ ARIAS* y M. Teresa RIVAS**
(*) Dpto. de Metodología de las Ciencias del comportamiento. Fac. de Psicología. UCM (**) Dpto. de Psicología Básica, Psicobiología y Metodología. Fac. de Fil. Y CC. EE. UM.
En este artículo se describe un modelo de teoría de respuesta al ítem no paramétrico -el modelo de Mokken-, elaboración probabilística de la escala determinista de Guttman. Se presentan los procedimientos para evaluar la escalabilidad y la fiabilidad dentro de este modelo. Para ejemplificar los cálculos y la utilidad del modelo para las escalas acumulativas de actitudes, se aplica el método a la construcción de una subescala de Reacciones Infantiles en la Adopción. Por último, se realiza un análisis crítico de las principales ventajas e inconvenientes del método.
Palabras Clave: TRI no paramétrica, escala de Mokken, holomorfismo, escalabilidad, fiabilidad.
Scale analysis: Mokken probabilistic method of dichotomous iteras responses.- This paper describe a nonparametric item response model -the Mokken scale-, a stochastic elaboration of the deterministic Guttman scale. The methods for estimating the reliability and the scalability within this model are presented. In order to illustrate the computation procedures and the utility of Mokken model for accumulative attitude scaling, the method is applied lo the constructor of the subescale of Children Reactions to Adoption. Finally, recommendation are given concerning the use of these methods.
Key Words: Nonparametric TRI, Mokken scaling, holomorphism, escalability, reliability.
INTRODUCCIÓN
La medición por medio de indicadores es frecuente en las ciencias en general, para obtener medidas de constructos subyacentes o no observables. Pueden adoptarse diversas aproximaciones, siendo una de ellas la denominada por Torgerson (1958) escalamiento basado en la respuesta, consistente en la medición conjunta de individuos x estímulos. Esta aproximación es especialmente útil en aquellos casos en los que por ausencia de criterios empíricos para la validación, deben buscarse las relaciones entre indicadores o ítems por medio de algún modelo matemático.
En esta línea y diferenciándose por el tipo de modelo propuesto, se han dado varios enfoques al tratamiento de los ítems dicotómicos, de las que dos han tenido gran relevancia en las aplicaciones: a) El modelo determinista de Guttman (1947, 1950 a, 1950 b), conocido como modelo de escala perfecta, o análisis de escalograma, que tuvo un gran impacto, así como una gran difusión y popularidad en su momento, como revelan la gran cantidad de estudios y variaciones sobre el modelo, tal como puede apreciarse en los textos sobre escalamiento. (Edwards, 1957; Torgerson, 1958; Sagi, 1959; Van der Ven, 1980). b) El modelo logístico de Rasch (Rasch, 1960, 1966), modelo paramétrico de naturaleza probabilística, que supuso una auténtica revolución en la medida de las diferencias individuales, en el que el concepto básico lo constituyen las denominadas «curvas características del ítem», basadas en la distribución logística. En este modelo se supone que las respuestas observadas se obtienen mediante probabilidades determinadas por un parámetro latente del sujeto (0) y un parámetro del ítem (R). Se caracteriza por la separabilidad de los parámetros del sujeto y del ítem, y ello es debido a que se opera con estadísticos suficientes. Bajo este modelo los estimadores de los parámetros son eficientes e independientes de la distribución particular de la población de la que se han extraído los datos.
Mucho menos conocido que los anteriores es el Modelo de Mokken (Mokken, 1971; Mokken y Lewis, 1982;. Mokken y Sytsma, 1986), que es una elaboración estocástica de la escala de Guttman y que puede considerarse componente de la familia de modelos de la Teoría de Respuesta al ítem, pero sin las restricciones paramétricas de los modelos conocidos, como el de Rasch. A pesar de algunas críticas recientes sobre las propiedades de escala de este modelo (Jansen et al., 1984; Roskam et al., 1986), su utilidad como modelo de medida se ha puesto de relieve en múltiples aplicaciones especialmente en las áreas de la Psicología Social y Política (Mokken, 1969; 1971; Gillespie et al., 1987) y en la Psicología Evolutiva (Kingma, 1984; Kingma y Reuvekamp, 1984), terreno este último donde se muestran como una alternativa importante a las escalas de Guttman tradicionalmente usadas. En el presente trabajo se ha realizado una aplicación concreta de dicho modelo a la elaboración de una Escala Acumulativa de «Reacciones Infantiles en la Adopción». Dada su escasa difusión entre los investigadores españoles, y en general fuera del contexto europeo, consideramos importante hacer una introducción del modelo y sus propiedades antes de presentar su aplicación.
EL MODELO PROBABILISTICO DE MOKKEN
1. Las escalas acumulativas
En numerosas situaciones de investigación, los sujetos responden a ítems puntuables dicotómicamente. Por ejemplo, imaginemos el conjunto de disposiciones que pueden tener los sujetos con relación a un determinado partido político: 1. Votar a dicho partido político; 2. Ser militante de dicho partido; 3. Trabajar activamente en el partido.
Sobre la base de la escala anterior, pueden distinguirse cuatro tipos de personas: a. Los que no votan al partido político. b. Los que simplemente votan al partido. c. Los que son militantes del partido., d. Los que trabajan activamente en el partido.
Podríamos hacer una representación gráfica de personas e ítems en un continuo unidimensional, definido como participación en el partido político, como la de la Figura 1.
Para llegar a este tipo de representación es preciso poder establecer relaciones de dominancia entre los ítems y sujetos, entendiendo que si un sujeto «domina» cierto ítem, domina también todos los de rango inferior, y si un sujeto «no domina» cierto ítem no dominará los de rango superior a éste. Una escala de este tipo debe ser unidimensional ya que los ítems se ordenan con relación a un único concepto subyacente. Cuando se trata de aplicar el modelo de la escala perfecta de Guttman a datos empíricos de este tipo, sus rasgos deterministas llevan a imperfecciones, ya que escalas e ítems perfectos raramente existen en la práctica y el problema fundamental de la escala es que supone la no existencia de error de medida. En la literatura psicométrica se han desarrollado diferentes técnicas para llevar a la práctica este modelo. En general, todas ellas consisten en diferentes operacionalizaciones del concepto de reproductividad (Loevinger, 1948; Goodenough, 1944; Guttman, 1950a, 1950b; Green, 1956; Moscovici y Durain, 1956), siendo éste una media del grado en que las respuestas a los ítems se pueden reproducir a partir de la puntuación total. No obstante esta medida de error es vaga e imprecisa. En general, en todas las aplicaciones del escalograma de Guttman subyace una pregunta: pueden deberse los bajos valores del índice de reproductividad a que los ítems están lejos de ser perfectos o a que el modelo determinista es poco realista? En general las respuestas apoyan esta segunda hipótesis y el modelo de Mokken es una elaboración estocástica entre los indicadores y el constructo subyacente y contempla en el índice de reproductivas o escalabilidad, efectos de respuestas debidas al azar.
2. Conceptos fundamentales del modelo de Mokken
Mokken formuló un modelo de dos parámetros que es una generalización del modelo de Guttman, con fuertes influencias de los modelos de estructura latente (Lazarsfeld y Hemy, 1968) y del rasgo latente (Rasch, 1960, 1966). Antes de exponer este modelo presentamos los conceptos básicos fundamentales para su mejor comprensión.
2.1. Items monótonos y Curva Cartacterística del ítem
Si un conjunto de sujetos contesta a una selección de ítems, entonces cada sujeto se mide en cada ítem en términos del concepto que se pretende medir y sus respuestas son el resultado de esta comparación. El contenido del ítem determina el comportamiento de la respuesta, que puede clasificarse parcialmente en dos tipos, definidos normalmente como éxito o fracaso.
La variable o constructo latente que se pretende medir y que se supone genera la respuesta positiva de los sujetos a los ítems se representa en el eje horizontal. Imaginemos el ejemplo anterior en el que la variable latente es el «grado de implicación de un sujeto con un partido político», que desconocemos. Un supuesto razonable es que cada sujeto que responde a un ítem tiene cierta cantidad de actitud latente, es decir, que cada individuo encuestado tiene una puntuación que puede situarse en algún punto de la escala de actitud. Esta cantidad de actitud se denota θ. En cada nivel de actitud θ habrα cierta probabilidad de responder positivamente al ítem, que representamos P(θ). Por tanto, para cada sujeto s compara su posición sobre este continuo con el contenido del ítem. Así, supongamos, en este ejemplo, todos los posibles «grados de participación» de los sujetos distribuídos sobre este eje. Un sujeto con un determinado grado o cantidad de atributo dará una respuesta positiva con una probabilidad que depende del grado en que posee este atributo. Si para todos los sujetos conociésemos el grado en que posee el atributo y sus respuestas al ítem, podríamos representar la probabilidad de respuesta positiva, como una función de la variable subyacente o atributo y representarla gráficamente mediante la denominada traza del ítem (Lazarsfeld, 1959) o curva característica del ítem (Lord y Novick, 1968).
Items monótonos son aquellos tales que, para dos niveles de atributo θ1 < θ2 entonces P(θ1) < P(θ2). La curva caracterνstica divide el continuo subyacente en dos intervalos, el que contiene la cantidad de atributo que requiere el ítem y el que no. Cuando existe una correspondencia uno-uno entre las dos alternativas y los dos intervalos en los que el ítem divide el continuo de interés nos encontramos ante el comportamiento característico de la Escala Perfecta de Guttman. Un ítem perfecto se caracterizará por una característica como la curva (a) de la figura 2. con probabilidades únicamente de 0 ó 1. En ella, solamente contestarían afirmativamente los sujetos que poseen el atributo en un nivel fijado. La curva característica (b) de la figura 2, representa la probabilidad de que un sujeto conteste afirmativamente a medida que lo hiciese el grado de afinidad de los sujetos con los principios del partido, es decir, será más probable que vote así un sujeto con un alto grado de afinidad, que otro con un menor grado.
Aplicando métodos de construcción de escalas al conjunto de los tres ítems del ejemplo, podríamos ordenar ítems y sujetos en el mismo continuo unidimensional: grado de afinidad con el partido. Como se ha dicho anteriormente, el conjunto de los tres ítems debe formar una escala acumulativa, de tal modo que si un sujeto contesta afirmativamente al ítem 2, debería hacerlo también con el ítem 1 y si contesta positivamente al ítem 3, debería contestar en este sentido a los dos anteriores. En la figura 3 se presenta la representación gráfica de las curvas características de los tres ítems según el modelo de la escala perfecta.
En la tabla 1 se muestran los distintos patrones de respuesta posibles al conjunto de los tres ítems. Los patrones de respuesta de escala perfecta, raramente se encuentran en la práctica, ya que en general habrá sujetos con altos valores del atributo que pueden dar respuestas negativas y viceversa. Por lo tanto, serán más realistas modelos con ítems simplemente monótonos como el de la curva b de la figura 2.
2.2. El holomorfismo de los ítems
El modelo de Mokken trata la aptitud, actitud o cualquier otro constructo o conducta de interés como un rasgo latente único sobre el que puede representarse la posición de la persona mediante un parámetro (θ) y la posición de un items por el parámetro δ. Dado un conjunto razonable de ítems unidimensionales (que miden el atributo latente), el parámetro θ de la persona puede estimarse por el número de ítems a los que una persona responde positivamente y el parámetro del ítem δ por la proporción de personas que responden positivamente al ítem. Es por lo tanto un modelo de dos parámetros, referidos el primero como la puntuación de la persona en la escala y el segundo, como dificultad del ítem. Los ítems que se ajustan al modelo de Mokken deben cumplir el supuesto del holomorfismo o de la doble monotonía.
Se ha visto anteriormente que la curva característica del ítem describe la relación entre la probabilidad de una respuesta correcta a un ítem y la escala de aptitud. El modelo de Mokken especifica la relación entre la probabilidad de una respuesta correcta a un ítem y la escala de aptitud. El modelo de Mokken especifica la relación entre la respuesta al ítem xi y la aptitud latente en términos de una curva característica del ítem, denotada por P(xi׀θj), que representa la probabilidad de una respuesta positiva al ítem i dado que el supuesto se encuentra en la posición j sobre el rasgo latente. A diferencia de los modelos de la Teoría de la respuesta al ítem que especifican la forma funcional de la relación, el modelo de Mokken no la especifica, de ahí su nombre de modelo de respuesta al ítem no paramétrico. La única restricción establecida por el modelo de Mokken es el supuesto de la doble monotonía, que le lleva a la definición de Curva Característica del Item Holomorfa, por las siguientes propiedades: Sea un conjunto de ítems dicotómicos y la función Φ, que depende de θ-parαmetro unidimensional del sujeto- y de δ, -parαmetro unidimensional del ítem y siendo denotada dicha función por π(θ,δ), la CCI Holomσrfica tiene las siguientes propiedades:
1. πi(θ,δ) es monσtonamente homogénea (Mokken y Lewis, 1982). Esta propiedad implica que para cualquier ítem de la escala de Mokken, la probabilidad de una respuesta positiva aumenta con incrementos de la aptitud θ, o más formalmente: para dos sujetos cualesquiera i y j, tales que θ¡ < θj, la probabilidad de una respuesta positiva a cualquier ítem de la escala es menor para la persona i.
2. δi < δj =πj (θ, δi) > πj (θ, δj). Este requisito expresa que para cualquier valor del rasgo latente θ, la probabilidad de una respuesta positiva decrece con la dificultad del ítem. Esto significa que el orden de las dificultades de ítem permanece invariante sobre los valores de θ o dicho de otra forma, que las curvas características de item no intersectan.
Los dos requisitos anteriores establecen el principio de la doble monotonía, supuesto básico del modelo de Mokken (Mokken, 1971; Mokken y Lewis, 1982). Las curvas características del ítem que satisfacen este principio se denominan Curvas Holomorfas, en denominación de Rasch (1960). Un conjunto de ítems cuyas C.C.I. son holomorfas se denomina holomorfo y aquellos ftems que violen la doble monotonía deben eliminarse del conjunto que se pretende constituya una escala.
PRUEBAS DEL MODELO DE MOKKEN
1. Homogeneidad monótona del conjunto de ítems
Para probar el requisito de homogeneidad monótona, Mokken desarrolló tres coeficientes relacionados de escalabilidad, todos ellos basados en los momentos marginales de pares de ítems o en general, en el supuesto de la independencia marginal. El primero de ellos, Hij mide el grado de homogeneidad o de asociación entre cada par de ítems. El segundo, Hi, mide la homogeneidad de un ítem particular con respecto al conjunto de los restantes ítems y se obtiene sumando los de los pares de ítems relevantes. El tercero, H, mide la homogeneidad de la escala como un todo, sumando los coeficientes de los ítems individuales. La base de todos estos coeficientes se encuentra en la tabulación cruzada de todos los pares de ítems, que permite determinar el grado de asociación entre dos ítems cualesquiera, ya planteada en el concepto de escalabilidad de Loevinger (1948). Consideremos un sujeto con un valor 0 en el rasgo latente y que responde a un ítem particular.
Designamos por xi la respuesta al ítem particular y por P(xi = 1Ιθ) = πi (θ), la probabilidad de que una persona con dicho nivel de rasgo de una respuesta positiva al νtem i. Bajo el supuesto de una población de N sujetos, consideramos que Ni es el número de sujetos de la misma que responden positivamente al ítem i.
Entonces:

Tomamos la convención de que la numeración de los ítems está de acuerdo con su dificultad decreciente, por tanto, para dos ítems cualesquiera i y j:
Supongamos que se tiene una muestra de k ítems de una población de ítems o universo de contenido y una población de sujetos que responde a estos ítems. Designamos dos de los ítems como i (fila) y j (columna). La tabla 2 representa las probabilidades de respuesta a dicho par de ítems.

Mokken (1971) tomó como punto de partida para las definiciones de la escalabilidad el clásico coeficiente debido a Loevinger (1948), para la reproductividad en el modelo de Guttman. Bajo este modelo, esperaríamos que la casilla superior derecha o «casilla error» debería estar vacía, es decir: πij (1,0) = 0.
Bajo la hipótesis de independencia estadística, anticiparíamos para i < j, que la proporción de dicha casilla sería igual al producto de las posibilidades marginales. Los tres coeficientes de escala pueden definirse en término de los parámetros manifiestos y de las probabilidades de la casilla del error πij (1,0) (donde i < j). Dada la ordenación de los ítems de acuerdo a sus valores δi, las probabilidades de la casilla error, π(e)jj pueden definirse como:
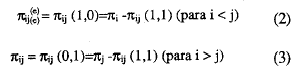
De la misma forma, las probabilidades esperadas de la casilla error, π(0) , bajo la hipótesis nula de independencia estadística son:
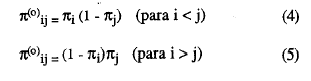
El índice de homogeneidad de dos ítems i y j. Hij, mide la diferencia proporcional entre la probabilidad de error esperada bajo la hipótesis nula de la independencia marginal y la probabilidad real de la casilla error, es decir:
![]()
o en términos de probabilidades:
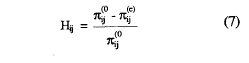
y teniendo en cuenta que:
![]()
Hij puede escribirse mediante:
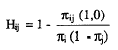
Y haciendo las sustituciones oportunas, Hij se convierte en:
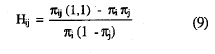
Cuando los dos ítems son independientes, Hij, será cero y cuando la casilla error está vacía, alcanzará el valor de uno. La agregación de estas probabilidades de error observadas, para todos los pares de ítems del conjunto de k, se define como:
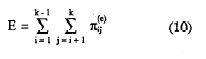
La agregación de las probabilidades de error bajo la hipótesis nula de independencia marginal, para el conjunto de k ítems se define como:
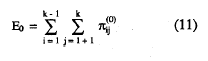
Con estas dos agregaciones de probabilidades, (10) y (11), puede definirse el coeficiente de homogeneidad global de la escala, H, como en (6), haciendo las sustituciones para el caso agregado:
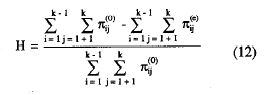
y teniendo en cuenta (8):
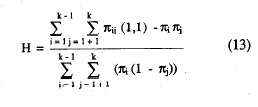
H será cero cuando todos los ítems sean mutuamente independientes y alcanzará el valor máximo de 1 cuando todas las casillas error de las distintas tablas 2 x 2 estén vacías. Dentro de la misma línea Mokken (Mokken, 1971; Mokken y Lewis, 1982), también propone el coeficiente de homogeneidad del ítem i, Hi, que puede demostrarse es análogo a la correlación ítem-total de la Teoría Clásica de los Test. (Sytsma y Molenaar, 1987). Agregando las probabilidades de error observadas para el ítem i, obtendríamos E¡ y haciendo lo mismo para las dadas bajo la hipótesis de independencia, las correspondientes Eoi. Del mismo modo que en (6) se puede definir el coeficiente de homogeneidad del ítem Hi, por
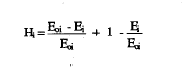
que equivale a:
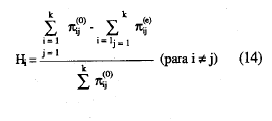
y teniendo en cuenta (8):
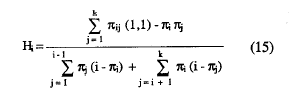
2. Estimadores muestrales de los coeficientes
Sea n una muestra de sujetos extraída aleatoriamente de la población de tamaño N, que responde al conjunto de k ítems. En la tabla 3 se presentan las respuestas de los sujetos a un par de ítems cualesquiera i y j. Los estimadores muestrales de las probabilidades error se definen, teniendo en cuenta la tabulación de la tabla 3, como
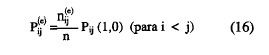
siendo nij(o) la frecuencia de la casilla error, nij (1,0)
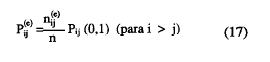
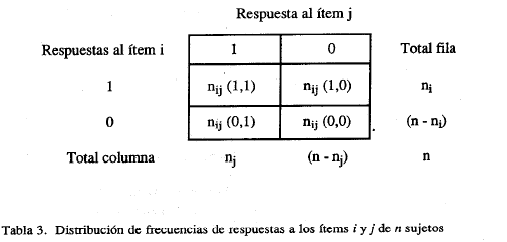
Las probabilidades error esperadas bajo la hipótesis de independencia marginal se definen como:

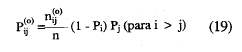
Las diferentes estimaciones pueden obtenerse fácilmente de la tabulación cruzada de las respuestas a cada par de ítems. Si la frecuencia observada en la celda de error es menor o igual que la frecuencia esperada bajo la hipótesis nula de respuesta aleatoria, existiría una correlación positiva entre los ítems. Teniendo en cuenta lo anterior, el índice Hij es un estimador del índice de homogeneidad del par, que mide la diferencia proporcional entre la frecuencia esperada bajo la hipótesis de independencia de la casilla error y la frecuencia real de la casilla y en términos de frecuencias absolutas viene dado por.
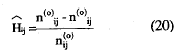
y en términos de frecuencias relativas o proporciones:
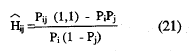
Cuando los ítems son independientes, este índice será cero; cuando la casilla error está vacía, será igual a la unidad. La estimación del coeficiente de homogeneidad del ítem, Hi viene dada por la ecuación
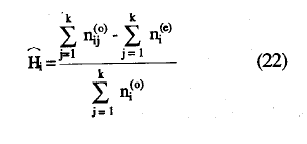
y en términos de proporciones
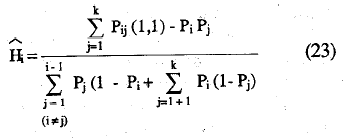
La estimación del coeficiente-de homogeneidad de la escala, H, se, obtiene mediante la siguiente ecuación:
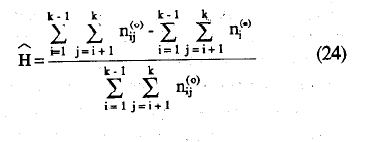
y en términos de proporciones
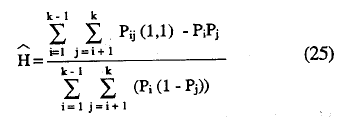
3. Contrastes acerca del coeficiente de escalabilidad (H).
Mokken (1971) desarrolló la teoría muestral para el estimador del coeficiente de escalabilidad ^H que proporciona las bases para llevar a cabo el contraste de la hipótesis de aleatoriedad en el patrón de respuestas, es decir, la hipótesis de aleatoriedad en el patrón de respuestas, es decir, la hipótesis nula de que el coeficiente de escalabilidad H es igual a cero. La prueba de hipótesis propuesta enfrenta las dos siguientes:
Ho : H=0 H1: H >0
La hipótesis alternativa, H1, se plantea únicamente de forma unilateral ya que 0 <_ H <_ 1.
Para la realización de dicho contraste se considera el estadístico Δ*, delta star, definido como
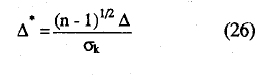
que tiende, para muestras grandes, a la distribución N(0,1) (Mokken, 1971, p. 163) y donde:
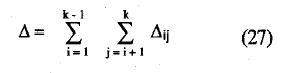
siendo Δij:
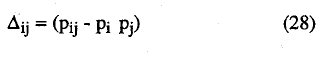
con varianza:
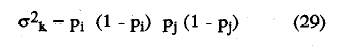
y siendo σk la desviación típica de Δ, que viene dada por la siguiente expresión:
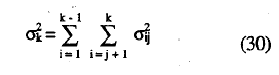
Fácilmente puede comprobarse que:
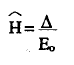
Un planteamiento alternativo de la hipótesis nula será, por tanto:
![]()
Para llevar a cabo dicho contraste basta con sustituir en (26) los valores de las expresiones correspondientes, que pueden obtenerse fácilmente a partir de los estimadores calculados a partir de las frecuencias de la tabla 3. La decisión de mantener la hipótesis nula viene dada por la regla:
![]()
Así como la de su rechazo a favor de la hipótesis alternativa (H>0): Δ*≥z1-α *
Para evitar el riesgo de capitalización del azar, se recomienda corregir el nivel de significación general a impuesto por el investigador, tomando a*:
donde a es el nivel de significación global para el conjunto de ítems, (es decir, alguno de los habituales valores 0,05, 0.01, etc). El test de la hipótesis nula es el primer paso para evaluar la escalabilidad de una muestra de ítems; no obstante, es conveniente evaluar también los ítems individualmente.
4.Contraste acerca de los coeficientes Hi
La evaluación de las propiedades de escalabilidad de cada uno de los ítems puede llevarse a cabo mediante tests análogos al anterior para los k coeficientes de homogeneidad Hi. Mediante este contraste se pone a prueba la hipótesis nula:
HO : Hi= 0
frente a la hipótesis alternativa:
H1:Hi>0
El estadístico de contraste se define como:
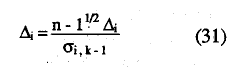
y tiende, para muestras grandes, a la distribución N(0,1) (Mokken, 1971, p. 163) y donde

siendo Δij igual que en (28). La σ2i,k-1 viene dada por la siguiente expresión:
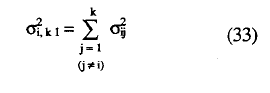
Para llevar a cabo dicho contraste basta con sustituir en (31) los valores de las expresiones correspondientes, que pueden obtenerse fácilmente a partir los estimadores obtenidos de las frecuencias de la tabla 3. La decisión de mantener la hipótesis nula viene dada por la regla:
Δ*i<z1-α
así como la de su rechazo en favor de la hipótesis alternativa (H > 0):
Δ*¡ ≥z1-α
La aplicación de este contraste a cada uno de los ítems es una condición previa para determinar la escalabilidad de los ítems, pero además es conveniente imponer requisitos adicionales sobre los valores de los coeficientes Hi de modo que la hipótesis nula verse sobre valores superiores a un valor cada c, mayor que 0, es decir
Hi≥c>0 => H≥c
El imponer requisitos más fuertes sobre c es especialmente importante al construir escalas de Mokken en áreas poco estudiadas (Kingma y Ten Vergert, 1985). El propio Mokken sugiere una clasificación de la adecuación de las escalas basada en los siguientes valores orientativos:
.50≤H escala fuerte
.40≤H <.50 escala media
.30≤H <.40 escala débil
Estos criterios, el de la escala como un todo y el de los ítems individuales, permiten al investigador juzgar si un conjunto de ítems constituyen una escala Mokken y que ítems deben ser eliminados. En la práctica, cuando un ítem no cumple estos criterios es eliminado de la escala. A continuación se calculan de nuevo los valores de los tres coeficientes, aplicando los sucesivos contrastes, hasta que se logre una escala suficientemente fuerte. Mokken (1971, pp. 1967) establece un procedimiento para fijar el nivel de significación α* de estos contrastes sucesivos.
5. Monotonía de las dificultades de los ítems
Las estimaciones de los coeficientes de escalabilidad se usan para probar la homogeneidad monótona de los ítems. Esta es una condición necesaria, pero no suficiente, ya que el modelo debe cumplir la doble monotonía. El test de monotonía de las dificultades de los ítems proporciona junto con el anterior una condición suficiente para la doble monotonía. La prueba de monotonía de las dificultades de los ítems supone una inspección de dos matrices P y PO, que contienen las probabilidades de dos respuestas positivas y de respuestas negativas, respectivamente, para todos los pares posibles de ítems. Este test está basado en otro supuesto del modelo de Mokken, el supuesto de la independencia estocástica local de las respuestas a los ítems, fijado el valor paramétrico del sujeto; es decir, las respuestas de los ítems son condicionalmente independientes, dado el valor θ, de modo que la probabilidad condicional de las respuestas conjuntas para personas con el mismo valor θ es igual al producto de las probabilidades marginales de estas respuestas. Se analizan las probabilidades no condicionales observables de cada par de νtems en las matrices P y P0. Puesto que se asume la independencia local dado θ, las probabilidades condicionales no observables implican las probabilidades no condicionales observables (Mokken, 1971).
Sea II = (πjj (1,1)) una matriz simétrica P de orden k de probabilidades manifiestas πij, sin especificar los elementos diagonales. Asumimos que las filas y las columnas se numeran de acuerdo a la ordenación de niveles de dificultad creciente de los ítems, es decir i < j , πi> πj , δi < δj. Así, las filas y las columnas están ordenadas respectivamente de izquierda a derecha y de arriba a abajo, según los niveles crecientes de la dificultad del ítem. Para cumplir parcialmente el requisito de la monotonía en las dificultades del ítem, los elementos de la fila í-ésima disminuirán monótonamente con el índice de la columna j y a causa de la simetría de la matriz, el mismo patrón se mantendrá para las columnas. Dicho en otros términos, la probabilidad de un par de respuestas positivas disminuirá en la matriz P de izquierda a derecha en cada fila y de arriba a abajo en cada columna. Algo similar debe observarse para la probabilidad de todos los pares posibles de respuestas negativas para concluir que los ítems seleccionados cumplen el requisito de monotonía en las dificultades de los ítems.
Sean II(0) = (πij (0,0)) una matriz simétrica Po de probabilidades manifiestas, donde P = πij (0,0) es la probabilidad de un par de respuestas negativas. En esta matriz, las filas y columnas se ordenan respectivamente de izquierda a derecha y de arriba a abajo según los niveles crecientes de dificultad. Los elementos de la fila i-ésima crecen monótonamente con el índice creciente de fila. En otras palabras, la probabilidad de un par de respuestas negativas decrecerá en la matriz de izquierda a derecha en cada fila y de arriba a abajo en cada columna. Para amplias muestras, los criterios de monotonía en las dificultades del ítem pueden probarse calculando los estimadores muestrales:
Obtenemos las matrices:
P = (Pjj (1,1))
P(O) = (Pij (0,0))
donde, teniendo en cuenta la tabla 3:
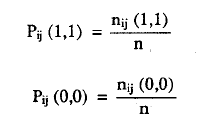
No se ha propuesto estadísticos de contraste específicos para la prueba de este supuesto. Mokken (1971) establece un teorema que justifica el examen únicamente de las probabilidades anteriores. Normalmente, en la práctica, se observa la matriz de dichas probabilidades. Algunos autores proponen la aplicación de un test de rachas (Kingsma y Taerum, 1988) para probar la significación estadística de las desviaciones del patrón esperado en las matrices P y Po. Un subconjunto de ítems se considera tipo escala de Mokken cuando éstos cumplen el criterio de doble monotonía, es decir, los datos están de acuerdo con los supuestos de homogeneidad monótona y de monotonía en las dificultades del ítem. Si los test no son satisfactorios, no podemos ordenar ítems y personas sobre el rasgo latente.
FIABILIDAD DE LA ESCALA DE MOKKEN
La aproximación de Mokken a la estimación de la fiabilidad evita el supuesto de la equivalencia de los ítems normalmente empleado en la teoría clásica de los tests, aunque adopta como punto departida la misma definición teórica. El supuesto de la doble monotonía permite un método de estimación del coeficiente de fiabilidad pxx que no se basa en la replicación ni en la consistencia interna. En la matriz P, los elementos no diagonales contienen las probabilidades de respuestas positivas a cada par de ítems si pudiésemos estimar los valores de la diagonal de esta matriz P, tendríamos una aproximación para todos los ítems de su probabilidad de una respuesta positiva sobre dos ocasiones diferentes. Esta probabilidad se denota por πi¡. La aproximación, similar al método test-retest, requeriría supuestos adicionales y propone la fiabilidad definida como la correlación que existe entre las distribuciones de respuestas correspondientes a pares de ítems equivalentes o paralelos. No obstante, debido a consideraciones teóricas y prácticas es imposible construir tales pares de ítems (Mokken, 1971, p. 144). Mokken obtiene un coeficiente de fiabilidad aproximado para conjuntos de ítems holomorfos. Para ello, tras ordenar el conjunto de ítems según su dificultad, δi < δj (i, j: 1, ... , k), se tiene:
Π2i < πii < πi y πii < πjj
además, mediante un teorema Mokken (1971, pp. 132), establece las cotas:
πi, i – 1, <πii <πi, I+1
Aunque πii no es estimable, las anteriores cotas permiten obtener sus valores mediante métodos aproximados, a partir de la matriz P = (p(1,1)).
Mokken ofrece dos aproximaciones para estos estimadores, denotados por πii, la de extrapolación y la de interpolación.
Mediante el primer procedimiento, se selecciona aquel de los dos valores Pi,i-1 o P¡,¡+1 para el que Pi - Pj sea menor, siendo j = i - 1 o j = i + 1 . Supongamos que sea este valor Pi,i+1 y asumiendo que las respuestas se comportan de una forma aproximada a la independencia estadística, podemos establecer la siguiente aproximación:
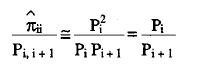
Despejando 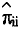 en la expresión anterior:
en la expresión anterior:
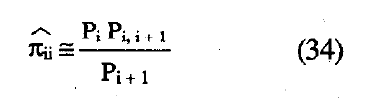
donde los elementos de la expresión se corresponden con valores de la
matriz P. Este procedimiento de estimación de la fiabilidad de los ítems
es válido para el conjunto i = 2, ... , k-1. Para los ítems 1
y k, debido a la ausencia de i-1 y de i+1, respectivamente, se necesita una
corrección, consistente en sustituir i-1 por i+1 y recíprocamente.
Por ejemplo, bajo nuestro supuesto de partida, de elegir i+1, necesitamos aplicar
la corrección para estimar ![]() ,
siendo:
,
siendo:
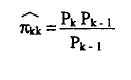
La segunda aproximación, utiliza la interpolación lineal:
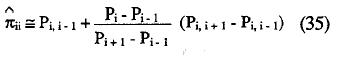
Por último define el estimador del coeficiente de fiabilidad de la escala total como:
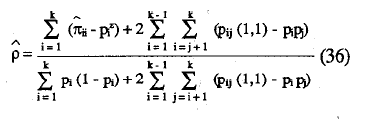
El valor del coeficiente se encuentra en el intervalo (0 ≤ p ≤ 1).
No se han dado cotas mínimas prácticas, no obstante la experiencia sugiere que, para considerar que la escala es fiable, el valor de p sea superior a 0,70. Las principales ventajas de este coeficiente son que no requiere el supuesto de paralelismo de los ítems y que no está influída por la longitud,
requiriendo únicamente que el conjunto de ítems sea holomorfo o doblemente monótono. En la práctica y con datos empíricos con dificultades iguales para varios ítems no son aplicables estos métodos, puesto que no pueden ordenarse los ítems y no se cumpliría el supuesto de holomorfismo. Sijtsma y Molenaar (1987) encontraron que al calcular los πii con el método de la extrapolación con Pi-1,i o con el de la interpolación usando Pi,i+1, los estimadores manifiestan un sesgo negativo, en tanto que haciéndolos por los procedimientos recíprocos respectivos, el sesgo es positivo. Estos autores proponen un nuevo procedimiento para la estimación del coeficiente del fiabilidad consistente en obtener los cuatro estimadores de πii la media de los mismos, para disminuir los citados sesgos. También proponen soluciones a algunos otros problemas, como el citado de dificultades iguales.
LA ACUMULATIVIDAD DE UNA ESCALA DE REACCIONES INFANTILES
Se aplicó el modelo de escalabilidad de Mokken al análisis de la «Escala de adaptación de padres en la adopción» (Téllez, 1990). Está constituida por varias subescalas independientes, que recogen diferentes aspectos del proceso de adaptación, referidos a inquietudes, impresiones, acomodación, etc. Cada una de ellas está formada por cuatro ítems que se pretende sean acumulados. De entre ellas se eligió la subescala de «Reacciones infantiles». Se aplicó a 92 sujetos (46 parejas), que habían adoptado un niño. La subescala que consideramos consta de los siguientes ítems, enumerados según su orden teórico:
1. Con la llegada de mi hijo percibí en él un ambiente de inseguridad.
2. He advertido perturbaciones en las reacciones de mi hijo.
3. Recuerdo manifestaciones agresivas del niño.
4. Recuerdo cambios de carácter manifestados en su comportamiento.
Se les pedía a los sujetos que contestasen si habían percibido o no la característica en cuestión. A partir del conjunto de respuestas se calcularon las proporciones para cada par de ítems, que se presentan en las tablas 4 a 9.


Los índices de dificultad de los ítems se presentan en la escala 10.

A partir de los datos anteriores se calcularon los coeficientes de homogeneidad monótona de los ítems y la escala. En la tabla 11, se muestran los Hii y los Hi, calculados, así como la significación estadística de los Hi.
El coeficiente H o índice de reproductividad de la escala alcanza el valor de .5378. El valor correspondiente a D* es de 6.5857, lo que nos permite rechazar la hipótesis nula con p < 0000 . Para examinar la monotonía en las dificultades de los ítems, se construyeron las matrices P y PO siguientes.


Una inspección de las matrices anteriores revela que el conjunto de
los 4 ítems es holomorfo y podemos pasar a evaluar la acumulatividad
y la fiabilidad de esta subescala. Puesto que el conjunto de ítems cumple
el principio del holomorfismo o de la doble monotonía, podemos considerar
que la subescala constituye una escala acumulativa, en el sentido Mokken. El
holomorfismo del conjunto de ítems permite calcular las aproximaciones
a los estimadores 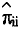 necesarios para hallar el estimador del
coeficiente de fiabilidad y que son estimaciones aproximadas de la fiabilidad
de cada ítem, entendida como repetición o como correlación
con un ítem equivalente. En la tabla 12 se muestran estos valores para
los cuatro ítems.
necesarios para hallar el estimador del
coeficiente de fiabilidad y que son estimaciones aproximadas de la fiabilidad
de cada ítem, entendida como repetición o como correlación
con un ítem equivalente. En la tabla 12 se muestran estos valores para
los cuatro ítems.
El valor obtenido para el coeficiente de fiabilidad de la subescala fue p = 0,7209. Podemos concluir por tanto que la subescala es relativamente fiable en cuanto a su consistencia intema.
Los cálculos del ejemplo fueron realizados con el programa MOKBAS (Rivas y Martínez, en prensa), un sencillo programa escrito en BASIC, que toma como input las tablas de contingencia de los pares de ítems.

CONCLUSIONES
En las páginas anteriores se ha presentado un modelo de Teoría de la respuesta al ítem no paramétrico, el modelo de Mokken, basado en un conjunto de supuestos más débiles que los de los modelos más conocidos de la TRI: a) unidimensionalidad del conjunto de ítems; b) independencia local estocástica; c) CCI monótonas no decrecientes; d) monotonía en las dificultades del ítem u ordenación idéntica para diferentes valores del rasgo (9).
Con el conjunto de supuestos anterior, se consigue un procedimiento de escalamiento de los sujetos, basado en la proporción o en el número de ítems «positivamente» respondidos del conjunto k. La ordenación «verdadera» de los sujetos en el continuo latente es estimada eficientemente por dicha puntuación de escala. Lo mismo se cumple también para la dificultad poblacional de los ítems y sus valores de escala. Desde el punto de vista de los modelos de construcción de escalas, creemos que el modelo presentado, introduce ciertas contribuciones interesantes:, a) Proporciona unas bases teóricas plausibles á la utilización del número de ítems «positivos», como índice de medida, basado en supuestos relativamente débiles, puesto que no asume formas paramétricas específicas. b) A partir de distribuciones marginales manifiestas, deriva las propiedades de homogeneidad monótona y holomorfismo, que permiten la ordenación única de ítems y de sujetos. c) Determina el grado de ecalabilidad de un conjunto de ítems en el sentido del escalograma o escala perfecta de Guttman, mejorando considerablemente su determinación.
A pesar de las reconocidas ventajas, el procedimiento no está exento de limitaciones, muchas de las cuales son producto de la primera de las ventajas citadas, la naturaleza no paramétrica del modelo, que impide afinar en los procedimientos de estimación.
Entre los principales problemas que presenta el modelo en estado actual y que pensamos se podían mejorar, se encuentran los siguientes: a) No define de forma inequívoca el concepto de, escala o al menos, lo que se entiende por tal desde la óptica de la Teoría de la Medición; define ésta a partir del coeficiente de escalabilidad. b) El coeficiente de escalabilidad, toma como criterio de definición el scalograma perfecto, junto con la independencia estadística, pero no permite evaluar de forma stadística el grado de desviación de la escala perfecta, ya que carece de estadísticos de bondad de ajuste. c) Precisa de una mayor justificación de la independencia de la muestra (de sujetos y/o de ítems) para algunos de los índices propuestos, como los coeficientes de homogeneidad y fiabilidad. Asimismo, justificación de la no dependencia de la muestra de ítems para la puntuación total, base para la ordenación de los sujetos. d) La prueba del holomorfismo, basada en una inspección visual, debería tener un apoyo estadístico. e) Sería conveniente desarrollar procedimientos de estimación de la «clase latente» ordinal del sujeto, en la línea de los desarrollos en estimadores de máxima erosimilitud propuestos recientemente (véase p. Ej. la compilación de Langeheine y Rost (1988). No obstante, ya Mokken y Lewis (1982) esbozan procedimientos bayesianos en este sentido. f) Su aplicación únicamente a ítems dicotómicos, aunque esta es una crítica que puede aplicarse en la práctica a casi todos los modelos de la Teoría de la Respuesta al Item. No obstante, Molenaar (1982, 1986; trabajos citados en Debster et al., 1989) presenta una extensión del modelo para ítems politómicos.
Algunos autores (Jansen et al. 1984; Roskam et al., 1986) hacen una durísima crítica del modelo, desde nuestro punto de vista, en parte injustificada, puesto que aluden a aspectos no implicados en el modelo de Mokken, tales como las pendientes de los ítems, sus distancias, etc. así como la ausencia de estadísticos suficientes para la estimación del rasgo. La consideración de estos aspectos, supondría la formulación de un modelo paramétrico, que no es el objetivo del modelo de Mokken. Un modelo de este tipo es el modelo de Rasch. En resumen, podemos considerar que el modelo de Mokken representa un desarrollo importante para la Psicometría, en el sentido de que cubre bastante bien, un espacio no cubierto por otros modelos y que resulta muy valioso en numerosas investigaciones, siempre que la variable de interés sea de carácter acumulativo y difícil de cuantificar, tal como se plantea en las investigaciones de Psicología del Desarrollo, de la Instrucción, etc. Su campo de aplicación no está limitado a estas áreas, como puede observarse en el ejemplo de aplicación presentado, así como en las referencias citadas en la introducción. Por otra parte, incluso con variables de cuantificación más fácil, puede ser aconsejable su uso en las primeras fases de construcción de instrumentos de medida, para seleccionar ítems, aunque en estadios posteriores pueda continuarse con modelos paramétricos como el modelo de Rasch.
REFERENCIAS
Debets, P.; Brouwer, E.; Sytsma, K. y Molenaar, I.W. (1989). MSP: A computer program for item analysis according to a nonparametric IRT approach. Educational and Psychological Measurement, 49, 610-613.
Edwards, A.L. (1957). Techniques of attitude scale construction. New York: Appleton Century Crofts.
Gillespie, M.; Ten Vergert, E.M. y Kingma, J. (1987). Using Mokken methods to develop robust cross-national scales: American and West German attitudes toward abortion. Social Indicators Research, 19, 74-95.
Goodenough, W.M. (1944). A Technique for scale analysis. Educational and Psychological Measurement, 4, 179-190.
Green, B.F. (1956). A method of scalogram analysis using summary statistics. Psychometrika, 21, 79-88.
Guttman L.A (1947) The Cornell Technique for scale and intensity analysis. Educational and Psychological Measurement, 7, 247-280.
Guttman, L.A. (1950a). The basis for scalogram analysis. En S.A. Stouffer et al. (Eds.). Measurement and Prediction. Princeton, N.J.: Princeton University Press.
Guttman, L.A. (1950b). Relation of scalogram analysis to other techniques. En S.A. Stouffer et al. (Eds.). Measurement and Prediction. Princeton, N.J.: Princeton University Press.
Jansen, P.G.W.; Roskam, E.E. y Van den Wollenberg, A.L. (1984). Discussion on the usefulness of the Mokken procedure for nonparametric scaling. Psychologische Beiträge, 26, 722-735.
Kingma, J. y Reuvekamp, J. (1984). The construction of a developmental scale for seriation. Educational and Psychological Measurement 44 1-23.
Kingma. J. y Ten Vergert, E.M. (1985). A nonparametric scale analysis of the development of conversation. Applied Psychological Measurement, 9, 375-387.
Kingma, J. y Taerum, T. (1988). A FORTRAN 77 program for a nonparametric item response model: The Mokken scale analysis. Behavior Research Methods. Instruments & Computers, 20, 471-480.
Kingma, J. y Taerum, T. (1989). SPSS-X procedure and standalone programs for the Mokken scale analysis: a nonparametric item response theory model. Educational and Psychological Measurement, 49, 101-136.
Lazarsfeld, P.F. (1959). Latent structure analysis. en S. Koch (ed.). Psychology: a study of a science, Vol. 3. New York: Mc Graw-Hill.
Lazarsfeld, P.F. y Henry, N.W. (1968). Latent Structure Analysis. New York: Houghton Mifflin.
Loevinger, J. (1948). The technique of homogenous tests compared with some aspects of «scale analysis» and factor analysis. Psychological Bulletin, 45, 507-530.
Lord, F.M. y Novick, M.R. (1968). Statistical theories of mental test scores. Readin, M.A.: Addison-Wesley.
Mokken, R.J. (1969). Dutch-American comparisons of the "sense of political efficacy". Quality and Quantity, 3, 125-152.
Mokken, R.J. (1971). A theory and procedure of scale analysis. Den Haag: Mouton.
Mokken, R.J. y Lewis, C. (1982). A nonparametric approach to the analysis of dichotomous item responses. Applied Psychological Measurement,6,427-430.
Mokken, R.J., Lewis, C. y Sytsma, K. (1986). Rejoinder to "The Mokken scale: a critical discussion". Applied Psychological Measurement, 10, 279-285.
Moscovici, S y Durain, G. (1956). Quelques applications de la théorie de l'information á la construction des échelles d'attitudes. L' année psychologique, 56, 47-57.
Rasch, G. (1960). Probabilistic models for some intelligence and attainment tests. Copenhagen: Denmarks Paedagogiske Institut.
Rasch, G. (1966). An individualistic approach to item analysis. En P.F. Lazarsfeld & N.W. Henry (Eds.). Readings in mathematical social science. Chicago, III: Science Research Associates.
Roskam, E.E.; Van den Wollenberg, A.L. y Jansen, P.G.W. (1986). The Mokken scale: A critical discussion. Applied Psychological Measurement, 10, 265-277.
Sagi, P.C. (1959). A statistical test for the significante of a coeficient of reproductibility. Psychometrika, 24, 19-27.
Sytsma, K. y Molenaar, I.W. (1987). Reliability of test scores in nonparametric item responsr theory. Psychometrika, 52, 79-97.
Téllez, J. (1989). Escala de adaptación de padres en la adopción. Málaga: Diputación Provincial.
Torgerson, W.S. (1958). Theory and Methods of Scalling. New York: Wiley.
Van der Ven, A.H.G.S. (1980). Introduction to Scalling. Chichester: Wiley.