Psicothema was founded in Asturias (northern Spain) in 1989, and is published jointly by the Psychology Faculty of the University of Oviedo and the Psychological Association of the Principality of Asturias (Colegio Oficial de Psicología del Principado de Asturias).
We currently publish four issues per year, which accounts for some 100 articles annually. We admit work from both the basic and applied research fields, and from all areas of Psychology, all manuscripts being anonymously reviewed prior to publication.
Psicothema, 1991. Vol. Vol. 3 (nº 2). 337-348
C. GOMEZ*, J. V. PICHARDO*, M. ESCUDERO** y G. JIMENEZ-RIDRUEJO***
*Lab. de Psicobiología. Dto. de Fisiología y Biología animal, U. Sevilla
**Lab de Neurociencia, Dto. de Fisiología y Biología Animal, U. Sevilla.
***Dto. de Biología, Facultad de Biología, UAM.
Eye position and the activity of 10 identified abducens motoneurons have been recorded during spontaneous eye movements in the alert cat. Total of 27 parameters were defined from recordings of eye position and velocity, from abducens motoneuron firing rate, and from a proposed double exponential model fitting motoneuron behavior during eye saccades. The principal component analysis was applied to these variables. Results suggest an independent coding of saccade duration and amplitude as well as confirm the validity of a double exponential as a description of motoneuron activity during the burst.
Key Words: saccadic movements, abducens motoneurons, principal component analysis, saccade skewness, oculomotor system, models, parametric control of movements.
RESUMEN
Control paramétrico de los movimientos oculares sacádicos mediante el análisis de componentes principales. Se registró la posición ocular y la actividad de 10 motoneuronas del núcleo del motor ocular externo durante movimientos oculares espontáneos en el gato alerta. Se definieron 27 parámetros de los registros de posición y velocidad ocular, de la tasa de disparo de las motoneuronas y de un modelo de doble exponencial que ajusta la tasa de disparo de las motoneuronas durante movimientos sacádicos. Un análisis de componentes principales fue aplicado a estas variables. Los resultados sugieren una codificación independiente de la duración y la amplitud del movimiento, así como confirman la validez de una doble exponencial como descripción de la actividad de las motoneuronas del VI par durante los brotes.
Palabras Clave: Movimientos sacádicos, motoneuronas del análisis de componentes principales, sesgo en las sacadas sistema oculomotor, modelos, control paramétrico del movimiento.
During saccadic eye movements abducens motoneurons (ABD Mns) show a burst of activity that encode the horizontal component of the movement. Very different approaches have been used in order to account for how ABD Mns encode saccades (Robinson, 1981; Fuchs, Kaneko and Scudder, 1985) and to define how the driving signal of the saccade is generated in the brainstem. In this sense, a main diagram has been proposed joining amplitude, maximun velocity and duration of saccadic eye movements (Bahill and Stark, 1979). This main diagram defines the general strategy for saccade generation, showing an exponential relation between amplitude, maximum velocity and saccade duration. However, for the range of these variables in the cat such a main diagram could be considered linear in a first approach (Goldberg, 1980). Also, ABD Mns show an activity burst related with eye saccade parameters that can be approached in very different ways: i) linear relationships have been described between different parameters of saccadic eye movements and parameters of the Mns firing rate burst, as maximum velocity versus maximum firing rate (Robinson, 1970; Fuchs and Luschei, 1970; Delgado-García, del Pozo and Baker, 1986; Gómez, Torres, B., Jiménez-Ridruejo and Delgado-García, 1986a) and burst duration versus eye saccade duration (Robinson, 1970; Fuchs and Luschei, 1970; Schiller, 1970); ii) a second approach is to consider the second order differential equation proposed to relate Mns activity and position, velocity and acceleration of the eye (Robinson, 1981), where Mn firing rate encodes in a continuous form for the eye variables. This model has been proved valid in monkey (van Gisbergen, Robinson and Gielen, 1981) and cat Mns (Torres, Gómez and Delgado-García, 1986); iii) reconstruction of possible Mns firing rate pattern by an inverse method using eye position registers (van Opstal, van Gisbergen and Eggermont, 1985); and iv) the proposal of a descriptive model of Mn burst during saccades. In fact it has been described that the firing rate burst can be modelled by a couple of exponential equations (rising and falling) (Pozo, Jiménez-Ridruejo, Delgado-García and Zoreda, 1984; Jiménez-Ridruejo, Pozo, Gómez and Delgado-García, 1983).
All these approaches have shown some general roles in the eye saccadic coding by Mns and saccadic generation strategy. Some of the more interesting are: with known saccade amplitude, peak velocity and duration can be modelled (Afifi and Azen, 1979); peak velocity is predicted by peak firing rate (Robinson, 1970; Fuchs and Luschei, 1970; Schiller, 1970) and the previous intervals (Gómez et al., 1986a); ocular mechanics can he predicted in a first approach as a second order linear model (Robinson, 1981), and the firing rate burst should be considered as a gradual firing rate increase instead of an abrupt jump (Jiménez-Ridruejo et al., 1983; Pozo et al., 1984; van Opstal and van Gisbergen, 1985). However, some questions still remain about the relationships between amplitude, velocity and duration in the strategy of saccadic generation and their coding by Mns (Evinger, Kaneko and Fuchs, 1981; King, Lisberger and Fuchs, 1986). Also, some kind of asymmetry can be observed inside the eye saccade (Baloh et al., 1975) (shorter in the rising than in the falling phase); how this asymmetry is coded in Mns is a question that still remains. Other minor questions can be also addressed. Finally, the validity of the descriptive double exponential model of Mns behavior during saccadic should be tested.
For these reasons a kind of multivariate analysis, the principal component analysis was applied to 27 parameters extracted during saccades from eye position and velocity registers, from ABD Mns activity and from the double exponential model. The goal of the principal component analysis is to reduce correlated variables to a small set of statistically independent linear combinations (Afifi and Azen, 1979; Frey and Pimentel, 1978). In a data set of P observations in a N multidimensional space (N variables measured in each observation), it is possible to produce a rotation of the axes that reduce the distance of the observations to the axes of the N-dimensional space (the reduction of the distance is called the explained variance). Also, it is possible to consider the N variables as a function of the P observations, a P-dimensional space in this case, then a rotation of the axes produces a reduction of the distance of the variables to the axes of the P-dimensional space. The latter is the geometrical interpretation used in present report. The analysis creates new axes (the principal components) where the variable are situated by their coordinates (the loading factors). So, the information contained in the actual data set can be reinterpreted by the position of the variables in the new space, variables that are in the same region covary directly and those situated in opposed regions covary inversely. Also the different positions of the variables on the same axe permit to interpret functionally the principal components.
MATERIALS AND METHODS
Under general anesthesia (35 mg/Kg, i.p), two adult cats were prepared for the recording of the electrophysiological activity of antidromically identified ABD Mns of the left ABD nucleus.
Simultaneousy the horizontal eye position was recorded by the search coil technique during spontaneous saccadic eye movements in the alert cat (Delgado-García et al., 1986; Gómez et al., 1986a). Recordings were stored on magnetic tape for subsequent analysis. Neuronal electrical activity was passed through a window discriminator and converted into a point process temporally correlated with occurring spikes (Gómez, Canals, Torres and Delgado-García, 1986b). Pulse trains and eye position recordings were digitized and then stored in a computer. A computer program was carried out to display on the screen the frequency histogram, the eye position and eye velocity (Fig. 1). The program provided two cursors to select the register positions chosen to calculate the parameters. This program permitted obtaining a series of 27 parameters defining the position and eye velocity, the Mn burst firing rate and the double exponential model describing rising and falling phases of the burst (Fig. 1A-C). Some of the parameters were calculated manually by positioning of the cursors as described above. Others were calculated by algorithms implemented in the program. The parameters of the descriptive model were calculated by fitting exponential equations to the rising and falling phase of the burst. The parameters of each exponential equation, time constant and asymptotic value, were fixed by hand. The values of the couple of exponential equations were calculated by the computer and compared by linear regression methods with the firing rate values stored during the burst. Afterwards, a new couple of exponential equations was automatically calculated changing the exponential equation parameters. Finally, the program selected as the valid couple of exponential equations those that reached the highest score in the linear correlation coefficient between exponential equation values and actual firing rate values. This iterative method permits to avoid possible distortions in the regression produced by the neccesary logarithmic transformation of the data to fit an exponential model. Given the few points used to calculate the regression inside the burst (4-10), the distortion could be significant if a standard linear regression model were used. If none of the calculated couple of exponential equations reached a minimum of 0.8 in the correlation coefficient value when plotted against firing rate burst values, that particular saccade was discarded for subsequent analysis.
From Mn firing rate the parameters considered were (Fig. 1C, bottom): Ric, firing rate previous to the burst; R, peak firing rate; If, firing rate increase in the burst; Rfc, firing rate at the end of the burst; Af, firing rate increase of the step; Dd, burst duration; Ts, rising time of the burst (time between peak firing rate and the time when firing rate falls 90% of the firing rate burst increase); Rps, slope of the firing rate rising phase; Nsu, number of spikes in the rising phase of the burst and Nba, number of spikes in the falling phase of the burst. The parameters considered from the double exponential model were (Fig. 1B, bottom): Asu, asymptotic value of the rising exponential; Bsu, time constant of the rising exponential; Aba, asymptotic value of the falling exponential; Bba, time constant of the falling exponential; Tsc, duration of the rising exponential. The parameters obtained from the horizontal eye register were (Fig. 1A and 1 B): P1, eye position before the saccadic movement (by convention negative values were from central eye position in the orbit to the left, and conversely positives to the right); P2, eye position after the saccadic movement; As, saccadic amplitude; Vmd, mean velocity; Vmax, maximum velocity; S, duration of the accelerating phase of the saccade: B, duration of the decelerating phase; Ds, duration of the saccade and A1, inverse of the time between two saccades, Le frequency of saccades, this parameter has been used as an alertness level index (Evinger et al., 1981). The latencies considered were (Fig. 1C): Lmv, latency between the onset of the burst and the onset of the saccadic movement; Tvf, latency between the peak firing rate of the burst and the peak velocity of the saccadic movement.
All these variables were analyzed using the principal component analysis (Afifi and Azen, 1979, Frey and Pimentel, 1978). Data in present analysis were obtained from 10 ABD Mns antidromically identified, where a number from 30-60 spontaneous saccades were analyzed (a total of 400 saccades were analyzed). All the values of the variables were standardized. The coil system used in the present experiments permits the recording of horizontal eye position, therefore saccades analysed in the present report should be considered as putative oblique saccades. The parameters of each saccade were stored in files created in the computer where a standard program of principal component analysis was applied (KM from the BMDP statistical library).
RESULTS
In Fig.1C (bottom) is shown the firing rate pattern of an ABD Mn, showing the typical pattern of burst activity during saccades proportional to eye velocity (Fig. 1C top), and the steady state phase proportional to eye position during eye fixation (Fig. 1A bottom).
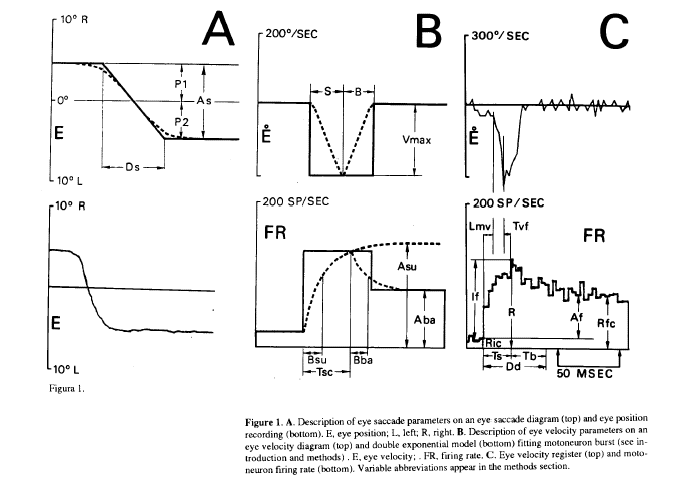
Figure 1. A. Description of eye saccade parameters on an eye saccade diagram (top) and eye position recording (bottom). E, eye position; L, left; R, right. B. Description of eye velocity parameters on an velocity diagram (top) and double exponential model (bottom) fitting motoneuron burst (see introduction and methods) . E, eye velocity; . FR, firing rate. C. Eye velocity register (top) and motoron firing rate (bottom). Variable abbreviations appear in the methods section.
The principal component analysis program used (KM from BMDP) provides a table of the explained variance (VP) by the calculated principal components (Table I), and the cumulative proportion of variance explained by each of the principal components (VA). Table I shows that the first 4 components account for 70% of the variance. 70% is a value of cumulative variance typical for not considering more loading factors in the interpretation of the analysis (Afifi and Azen, 1979; Frey and Pimentel, 1978). However, given that the two first components account for 52% of the total variance, and in order to simplify the interpretation results, only the first two axes were considered. For identical reasons the same criterion was used in the other 9 analyzed Mns. Also in Table 1 appear the calculated new coordinates (loading factors) of the variables for each component. The loading factor values permit plotting of the eye saccade, Mns and model parameters in an ideal plane formed by the orthogonal intersection of the ideal calculated axes (Fig. 2).
The plot of the loading factors for components I and II for the Mn analyzed in table I is shown in Fig 2. When the same analysis was performed for all the Mns registered, a similar position and grouping of the variables was obtained. For this reason, curves were traced by hand in order to group the set of variables that i) appear in the same area of the plane traced by componente I and II in all the analized Mns, and ii) their positions were constant in this plane in at least 8 of the analized Mns. Three groups ( 1,2,3) of variables appear in defined positions in the plots (Fig. 2). Group 1 include parameters from the eye saccade as As, Vmax, Vmd and S, but also parameters from the burst as If and Af. The variables included in group 2 are exclusively variables from the burst as R, Rfc and Rps. The group marked as the 3 included variables from the eye saccade as P1, B, and Ds, from the Mn firing rate as Nsu, Dd and Ts and also contains some parameters from the exponential model as Tsc and Bsu. Other variables appear outside these groups, P2 from the eye saccade, Tb, Ric and Nba from the Mn firing rate and Asu, Aba and Bba from the exponential model. The latency variables Lmv and Tvf and the alertness measure (Al) also appear outside these groups.
The principal component analysis program ( P4M) also provides the linear correlation matrix of the considered variables. The linear correlation matrix of variables for Mn shown in Fig. 1 and Fig. 2 is presented in table II. The absolute values whose linear correlation coefficient was consistently .5 in the 10 analyzed Mns are marked by an asterisk in table II. The sign of the linear correlation can be interpreted considering the variables in the horizontal file of the matrix as the abcissa and the variables in the vertical row of the matriz as the ordinate. In any case, results from the correlation matrix will be used only to support conclusions that are not obvious from the variable arrangement plot provided by the principal component analysis program.
A total of 400 Mn firing bursts were tested by the double exponential model (see methods). 18% were discarded for subsequent analysis because the relationship between Mn firing rate and the calculated double exponential did not reach the .8 level explained in the methods section.
DISCUSSION
The most powerful use of principal component analysis arise from the possibility of grouping variables by their coordinate proximities in the ideal orthogonal axes created by the analysis (Afifi and Azen, 1979; Frey and Pimentel, 1978). The variables that are situated in the same area of this ideal space are variables that covary, which means that they should have the same proximal cause or that some of the variables could be the cause of the others. In addition, the variable distribution along the axes could give some physiological significance to the mathematically calculated axes. With this perspective the 3 groups of variables found in eye saccades, Mns burst and the descriptive model will be discussed.
Group 1 reflects the known fact that amplitude (As) and peak velocity (Vmax) are linearly related (Goldberg, 1980), and that peak velocity of saccades (Vmax) is also linearly related with firing rate increase (If) in the burst (Robinson, 1970; Fuchs and Luschei, 1970; Schiller, 1970; Delgado-García et al., 1986; Gómez et al., 1986a). Also this group 1 associates the firing rate increase in the step (Af) with variables defining eye saccade and burst increase parameters, a fact expected from current models of saccadic generation that assume a step command calculation from the mathematical integration of the pulse signal generated by burst neurons (Robinson, 1981; Fuchs et al., 1985). In addition, the presence in this group of the saccade mean velocity (Vmd) with maximun velocity (Vmax) is coherent with results in oblique saccades of cats, monkeys and humans (Evinger et al., 1981; King et al., 1986), where they found a linear relationship between peak and average component velocity. It can be concluded that the amplitude, peak velocity and average velocity of the saccade are coded by the step and pulse commands (Robinson, 1970). The presence of the accelerating phase duration (S) in group 1 supports the Evinger conclusion (1981) that this period of time should be critical in determining saccade amplitude.
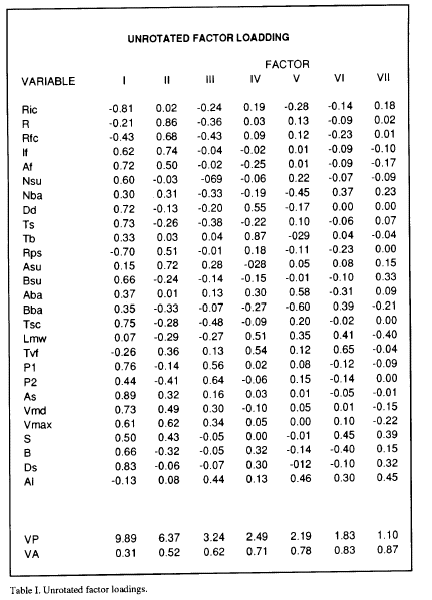
Figure 2. Principal component diagram of the first two ares. Variable coordinates are obtained from the unrotated factor loading table. Variable abbreviations appear in the methods section.
Group 2 includes variables exclusively from the Mn, with a high linear correlation coefficient between all the variables in the group (R, Rfc, Rps ). It should be considered that the slope of Mns increase of firing rate during the burst (Rps) is related with maximum firing rate (R) and with the initial firing rate (Ric) but not with the absolute value of firing rate increase (If). This fact could be related with a higher excitability of Mns or by a more abrupt input from pontine burst neurons if the Mn has been previously depolarised. It is impossible with the present set of data to decide between the two hypotheses. However, present data suggest that direct experimentation on intracellular register of ABD Mns should be neccesary to prove a possible higher excitability of membranes if the Mn has been previously depolarized. Research on intracellular ABD Mns has not checked this question (Barmack, 1974; Grantyn and Grantyn, 1978). On the other hand, the high linear correlation of final firing rate (Rfc) with the other two variables in the group should be interpreted by the fact that a higher firing rate end state is more probable if a high peak frequency is reached.
Group 3 mainly is a group where duration variables from the burst and from the eye saccade appear. In fact, from the 7 duration variables considered in the present study, Ds, S and B from the saccade; Dd, Ts and Tb from the burst and Tsc from the exponential model, 5 of them (Ds, B, Dd, Ts and Tsc) lie in group 3, and S and Tb are the only variables situated outside this group. First of all, a high linear relationship appears between Mn burst duration and eye saccade duration, a basic result previously described in ABD Mns studies (Fuchs and Luschei, 1970; Schiller, 1970; Henn and Cohen, 1973). Given that cat pontine burst neurons do not code the duration of the horizontal component of eye saccade in the burst duration (Kaneko, Evinger and Fuchs, 1981) , some coupling mechanism should exist between cat pontine burst neurons and ABD Mns in order to match burst Mn duration and the desired eye saccade duration. On the other hand, saccade profile skewness is a known fact (Baloh, Sills, Kumley and Honrubia, 1975), where the accelerating phase is shorter than the decelerating phase of the saccade. Present results show that the rising time of the burst (Ts) and the accelerating phase of the saccade (S) do not lie in the same group of variables and there is no significant correlation between them. In the same sense, falling time of the burst (Tb) and decelerating phase of the saccade (B) do not lie in the same group, although a better correlation is found between them. However, in the 10 registered Mns the ratios Ts/Tb and SB are less than 1 (ranges 0.4-0.7 and 0.4-0.9 respectively, data not shown). This result suggests that saccade skewness is coded by Mn firing rate skewness, but the irregularity in the particular time when peak firing rate is reached blurs the possible relationships between Ts with S and Tb with B. In group 3 the eye position before the saccade (P1) also appears. This result can be interpreted by the positive correlation of the eye position with the variables in this group, and the negative relationship with variables in group 2 plus Ric. This negative relationship between P1 and Ric is due to the convention used (right eye position positive, left eye position negative and Mn recording site in the left abducens). Presence of Nsu in group 3 can be explained by its tight relatric fixation of the desired saccade amplitude by duration and maximum velocity suggests the possibility that the saccade coding could be parametric and not continuously generated by the motor error signal as present saccade generation models propose (Robinson, 1981; Fuchs et al., 1985). Present analysis of eye and Mn parameters cannot by itself demonstrate the latter suggestion but it shows a deep parametric structure in the encoding of saccades by Mns.
With respect to the descriptive double exponential model (Jiménez-Ridruejo et al., 1983; Pozo et al., 1984) for the firing rate burst of Mns checked in the present report, its validity as a good predictor of Mn firing rate during the burst is confirmed by the fact that 82% of analyzed saccades bursts was accepted for subsequent analysis with the 8 linear correlation coefficient level described in methods. In addition, validity can be tested by the correlation between the model parameters and their corresponding Mn burst parameters. In this sense, time duration of the rising exponential (Tsc) is correlated with the rising time of the burst (Ts); the time constant of the rising phase of the exponential (B su) is inversely related with the slope of the burst rising phase (Rps); asymptotic value of the rising exponential (Asu) is related with the peak firing rate (R) and asymptotic value of the falling exponential (Aba) with the final firing rate (Rfc). All these results suggest as valid the proposed (Jiménez-Ridruejo et al., 1983; Pozo et al., 1984) double exponential model. Such a modulation has been proved to occur in ABD Mns 11 and to be neccesary to explain saccade profiles (van Opstal and van Gisbergen, 1985). For these reasons the exponential firing rate modulation should be incorporated in simulation models of the oculomotor system (Bahill and Stark, 1979; Fuchs et al., 1985; Robinson, 1981).
REFERENCIAS
Bayes, R. (1984): Análisis del efecto placebo. Quaderns de Psicologia, 8, 1, 161-183.
Beecher, H. K. (1955): The powerful of placebo. Journal of the American Medical Association,176: 1102-110.
Beecher, H. K. (1972): The placebo effect as a non-specific force surrounding disease and the treatment of disease. En R. Janzen, W.D. Keidel, A. Herz, C. Steichele, J.P. Payne y R.A. Burt (eds.): Pain: basic principles pharmacology-therapy. Baltimore: Williams and Wilkins.
Beecher, S. S. (1976): Clinical applications of attribution theories. En S.S. Brehm: The application of social psychology to clinical practice. Publishing Corporation. Recogido en C. Botella: Aportaciones a la Psicoterapia. Valencia. Promolibro.
Byerly, H. (1976): Explaining and exploiting placebo effects. Perspectives in Biology and Medicine, 19: 423-436.
Dobrilla, G. (1987): Placebo and placebo effect, general aspects and extent of the problem. Scandinavian Journal of Psychology, 11-16.
Choliz, M. (1988): Criticas y propuestas en torno al concepto placebo. II Congreso Nacional de Psicología Social. Alicante.
Choliz, M. (1989): Biofeedback y efecto placebo: análisis de las variables inespecíficas en el tratamiento de cefaleas mediante Biofeedback-EMG. Valencia. Tesis doctoral no publicada.
Elton, D.; Stanley, G. y Burrows, G. (1983): Psychological control of pain. Sydney. Grune and Stratton.
Evans, F. (1974): The placebo response in pain reduction. Advances in neurology, 4: 289-296.
Fish, J. M. (1973): Placebo therapy. San Francisco: Jossey Bass.
Frank, J. D. (1961): Persuasion and healing. Baltimore: Johns Hopkins Press.
Grunbaum, A. (1981): The placebo concept. Behavior Research and Therapy, 19: 157-167.
Grunbaum, A. (1986): The placebo concept in Medicine and Psychiatry. Psychological Medicine, 16: 19-38.
Henry, W. (1985): The time-released placebo: A reply to Critelli and Neumann. American Psychologist, 239.
Herrnstein, R. J. (1962): Placebo effect in the rat. Science,138: 677-678.
Kirsch, I. (1985): The logical consequences of the common factor definition of the term placebo. American Psychologist, 237-238.
Korchin, S. J. y Sands, S. H. (1983): Principles common to all psychotherapies. En C.E. Walker (ed.): The handbook of clinical psychology, vol 1. Dow Johns-Irwin. Traducido al castellano en C. Botella: Aportaciones a la psicoterapia. Valencia: Promolibro Leslie, A. (1954): Ethics and the practice of placebo therapy: American Journal of Medicine, 16:770-777.
Lieberman, L. R. (1985): Comment on Critelli and Neumann's "The Placebo". American Psychologist, 40: 238-239.
Mahoney, M. J. (1977): Cognitive therapy and research. A question of questions. Cognitive therapy and Research; 1.
Park, L. C. y Covi, L. (1965): Nonblind placebo trial. Archives of General Psychiatry, 12: 336-345.
Patterson, C. H. (1985): What is the placebo in Psychotherapy? Psychotherapy,22: 163-169.
Peek, C. J. (1977): A critical look at the theory of placebo. Biofeedback and Self-Regulation, 2: 327-335.
Rosenthal, D. y Frank, J. (1956): Psychotherapy and the placebo effect. Psychological Bulletin, 53: 294-302.
Shapiro, A. K. (1964): A historic and heuristic definition of the placebo. Psychiatry, 27: 52-58.
Shapiro, A. K. (1971): Placebo effects in medicine, psychotherapy, and psychoanalysis. En A. Bergin y S. Gardfield (eds.): Handbook of Psychotherapy and Behavior Change. New York: Wiley.
Shapiro, A. K. y Morris, L. A. (1978): The placebo effect in medical and psychological therapies. En S.L. Garfield y A.E. Bergin (eds): Handbook of psychotherapy and behavior change. New York: Wiley. Snyder, M.; Schulz, R. y Jones, E. E. (1974): Expectancy and apparent duration as determinants of fatigue. Journal of Experimental Social Psychology, 29: 426-434.
Thome, F. C. (1952): Rules of evidence in the evaluation of the effects of psychotherapy. Journal of Clinical Psychology, 8: 38-41.
Ullmann, L. P. y Kransner, F. (1969): Cognitions and behaviour therapy. Behavior Therapy, 1: 202-204.
Voudouris, N. J. (1981): The condicionability of positive and negative effects in experimental pain. Tesis doctoral no publicada. La Trobe University, Bundoora, Victoria.
Voudouris, N. J.; Peck, C. L.; Connie, L. y Coleman, G. (1985): Conditioned placebo responses. Journal of Personality and Social Psychology, 48: 47-53.
Wickramasekera, I. (1977): The placebo effect and medical instruments in biofeedback. Journal of Clinical Engineering, 2,3: 227-230.
Wickramasekera I. (1980): A conditioned response model of the placebo effect. Predictions from the model. Biofeedback and Self-Regulation, 5: 1, 5, 18.
Wilkins, W. (1985): Placebo Controls and Concepts in Chemotherapy and Psychotherapy Research. En L. White; B. Tursky y G. Schwartz (1985): Placebo: Theory, Research and Mechanisms. New York: Guilford Press.
Wilkins, W. (1986): Placebo problems in Psychotherapy Research: Social-psychological alternatives to chemotherapy concepts. American Psychologist, 41: 551-556.
Zanna, M. y Cooper, J. (1974): Dissonance and the pill: An attribution approach to studying the arousal properties of dissonance. Journal of Personality and Social Psychology, 29: 705-709.