Psicothema was founded in Asturias (northern Spain) in 1989, and is published jointly by the Psychology Faculty of the University of Oviedo and the Psychological Association of the Principality of Asturias (Colegio Oficial de Psicología del Principado de Asturias).
We currently publish four issues per year, which accounts for some 100 articles annually. We admit work from both the basic and applied research fields, and from all areas of Psychology, all manuscripts being anonymously reviewed prior to publication.
Psicothema, 1999. Vol. Vol. 11 (nº 1). 183-193
José Luis Padilla García, Cristino Pérez y Andrés González
Universidad de Granada
El interés por la unidimensionalidad ha aumentado en los últimos años por su relevancia para los modelos más populares de la Teoría de Respuesta a los Items. Sin embargo, las dudas sobre el cumplimiento del supuesto en el caso de los tests de rendimiento son generalizadas. De ahí su sustitución por versiones más débiles, por ejemplo, la de «unidimensionalidad esencial» (Stout, 1987). Presentamos los resultados de un estudio experimental sobre el efecto de las diferencias en las experiencias instruccionales en la «unidimensionalidad esencial» de las respuestas a un test de rendimiento. El procedimiento DIMTEST identifica la falta de unidimensionalidad esencial en un conjunto de 9 ítems (p<0.001), diseñados para medir el rendimiento en un contenido objeto de diferentes estrategias instruccionales para dos grupos de personas (N = 650). Por último, el trabajo analiza las implicaciones de los resultados para un posible funcionamiento diferencial del conjunto de ítems.
Effect of instruction on dimensionality of tests. The concern for this topic spreads for its relevance for the most popular models of Item Response Theory. Nevertheless, the doubts on the fulfillment of the assumption of unidimensionality in the case of achievement tests are generalized. Doubts that have led to the substitution of the original concept for weaker versions, for instance, the «essential unidimensionality» (Stout, 1987). This paper presents the partial result of an exploratory study, developed to examine the effect on the response dimensionality to an achievement test of the differences in instructional experiences. DIMTEST procedure (Stout, 1987) identifies the lack of essential unidimensionality in the set of 9 ítems (p<0.001) designed to assess achievement in content subject to different instructional strategies for two grupos of examines (N=650). Lastly, this paper analyses the consequences of results for a possible differential functioning of the set of ítems that not met the requirement of essential unidimensionality.
El estudio de la unidimensionalidad recibió un fuerte impulso en los años 80 por su importancia para los modelos más populares de la Teoría de Respuesta a los Items (TRI) (Hambleton y Rovinelli, 1986). Interés estimulado por la constatación inmediata de que el cumplimiento estricto del supuesto con datos reales no era posible (Lord, 1980; Hambleton y Swaminathan, 1985). La versión ampliamente compartida hoy día plantea que factores cognitivos, de personalidad y otras características de las personas y de la situación de evaluación, pueden influir en las respuestas a los ítems, junto con la supuesta habilidad medida por el test.
Este temprano sentimiento de frustración no ha restado valor al estudio del supuesto. La relevancia del mismo para la habitual «interpretación unidimensional» de las puntuaciones en los tests es apuntada por Stout (1987). Además, la aproximación más prometedora para la explicación del sesgo en los ítems parte de los posibles incumplimientos de la unidimensionalidad asumida por el test (Camilli y Shepard, 1994; Padilla, Pérez, González y Rojas, 1997). El estudio de la unidimensionalidad ha generado numerosos procedimientos e índices para examinar su cumplimiento. Muñiz y Cuesta (1993) realizan una revisión general de los métodos actualmente disponibles. También es recomendable consultar el análisis aplicado y las sugerencias prácticas aportadas por Ferrando (1996).
Las dudas sobre el cumplimiento del supuesto han sido especialmente claras en el caso de los tests de rendimiento (Goldstein, 1980). Junto con la coincidencia sobre la constante presencia de más de un factor o componente dominante en la evaluación de numerosos dominios del rendimiento, se mantienen discrepancias sobre el efecto en la dimensionalidad de las diferencias en la educación y aprendizaje que reciben las personas. Por ejemplo, Birenbaum y Tatsuoka (1982, 1983) mostraron el efecto «homogeneizador» de la instrucción, al ser mayor el número de factores en las situaciones preinstrucción que en las post-instrucción; mientras que, Traub (1983) defiende con firmeza que las diferencias instruccionales provocan la violación del supuesto de unidimensionalidad.
La fuerza de los argumentos y evidencias ha traído como resultado: (1) el desarrollo de una línea de investigación sobre la robustez de los modelos de la TRI ante el incumplimiento del supuesto (Cuesta y Muñiz, 1994; Martínez-Cardeñoso, Cuesta y Muñiz, 1996); y (2) la propuesta de modificaciones a la concepción clásica del supuesto (Cuesta, 1993).
Una de las modificaciones más fructífera es la realizada por Stout (1987, 1990), para quién el problema de la concepción clásica es no distinguir entre dimensiones «mayores» y «menores» a la hora de explicar la ejecución de las personas en el test. Considera más acertado contar, además de con una habilidad o factor dominante, con dimensiones menores que influyan en la respuesta a conjuntos de ítems, e incluso, sólo a ítems individuales. De ahí, que proponga sustituir la definición clásica por la más débil, pero psicológicamente más apropiada de «dimensionalidad esencial». Este concepto deriva de su teoría de la «independencia esencial». La definición formal de ambos conceptos es:
Definición 1 (Stout, 1990). La población de ítems U es «esencialmente independiente» (EI) con respecto a las variables latentes Θ , si U satisface para todo θ
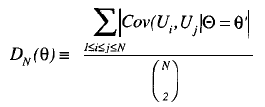
donde Ui y Uj, denotan las respuestas a cualesquiera ítems i y j respectivamente, Θ es el vector aleatorio de rasgos latentes y θ es un valor particular de Θ.
Definición 2 (Stout, 1990). La dimensionalidad esencial (dE) de una población de ítems U es la dimensionalidad mínima necesaria para satisfacer el supuesto de independencia esencial. Cuando dE = 1, se cumple el supuesto de unidimensionalidad esencial.
Hattie, Krakowski, Rogers y Swaminattan (1996) consideran que la unidimensionalidad esencial es la operacionalización de la versión débil del principio de independencia local.
Desde esta perspectiva teórica, el objetivo del estudio es examinar los efectos de las diferencias en las experiencias instruccionales sobre la «dimensionalidad esencial» en las respuestas a los ítems. El efecto sobre la dimensionalidad es examinado con el procedimiento estadístico DIMTEST (Stout, 1990). Las diferencias en las experiencias instruccionales son el resultado de utilizar estrategias instruccionales diferentes para la enseñanza de un mismo contenido. La aplicación del procedimiento DIMTEST y la manipulación instruccional realizada son detalladas a continuación.
Procedimiento DIMTEST
El procedimiento DIMTEST fue desarrollado por Stout (1987) para examinar la hipótesis de que en un conjunto de respuestas a los ítems existiera una sola dimensión dominante (i. e. «unidimensionalidad esencial»), más tarde fue optimizado por Nandakumar y Stout (1993). La hipótesis examinada se suele expresar así:
Ho : dE = 1 versus H1: dE > 1
La aplicación del procedimiento supone que un grupo de J personas responden a un test con N-ítems. Los ítems proceden de una población generada por la continuación del proceso de construcción de ítems de la misma forma que para los N-ítems. El sistema de puntuación produce un vector de respuestas dicotómicas, con el 1 para las respuestas conectas y el 0 para las incorrectas. También supone que la independencia esencial se cumple con respecto a alguna habilidad dominante Θ, y que las funciones de respuesta a los ítems son monotónicas con respecto a dicha habilidad.
El procedimiento se aplica en diferentes pasos. Aquí, sólo los resumiremos, resaltando los aspectos más relevantes para este estudio (para más información, Nandakumar y Stout, 1993; Stout, 1987).
Paso 1. Seleccionar un subgrupo de M ítems del test de longitud N. Los M ítems elegidos deben ser tan unidimensionales como sea posible y ser dimensionalmente distintos al resto de los ítems. Este conjunto forma el subtest de evaluación uno (AT1). Para elegir los ítems de AT1 se puede recurrir a tres procedimientos: (1) la opinión de expertos o el análisis subjetivo; (2) un análisis de componentes principales a partir de la matriz de correlaciones tetracóricas entre los N-ítems del test, en este caso, los ítems para AT1 son aquellos con una mayor carga factorial en el segundo factor antes de la rotación; y (3) un análisis de cluster jerárquico (Roussos, Stout y Marden, 1993). La elección de un procedimiento u otro para formar AT1 esta relacionada con el objetivo por el que el investigador decida utilizar DIMTEST (Stout, 1987).
Paso 2. Seleccionar un segundo subgrupo de M ítems del resto de los ítems que sean de dificultad similar a los ítems de AT1. Estos ítems forman el subtest de evaluación AT2. Este subtest es elegido automáticamente por DIMTEST y utilizado para corregir el posible sesgo estadístico por la semejanza en la dificultad de los ítems de AT1.
Paso 3. El resto de los ítems (n = N-2M) forman el subtest de agrupamiento PT. El objetivo del subtest PT es dividir a las personas en grupos por sus puntuaciones totales en PT; es decir, todas las personas que obtienen la misma puntuación total en PT son asignados al mismo subgrupo k (k=1, 2,......K).
Si se utiliza el análisis factorial para seleccionar AT1, la muestra de J personas es dividida en dos grupos. Las respuestas de un grupo son utilizadas en el análisis factorial para seleccionar AT1, y las respuestas del otro para calcular el estadístico T de Stout.
Paso 4. Dentro de cada subgrupo k, las respuestas a los ítems de los subtests AT1 y AT2 son utilizadas para calcular el estadístico T unidimensional, cuya expresión es:
T = ( T1 - T2 ) / √2
T1 se calcula con las respuestas a AT1 y T2, con las respuestas a AT2, en ambos casos:
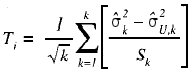
Las expresiones para σ 2k y σ 2U,k son presentadas a continuación. La expresión de la estimación habitual de la varianza para el subgrupo k es:
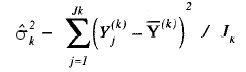
donde
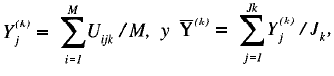
con Uijk, (1 o 0) representando la respuesta al item i por la persona j en el subgrupo k, y Jk el número total de personas en el subgrupo k. La estimación de la varianza «unidimensional» se obtiene con la expresión:
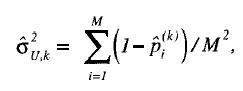
donde
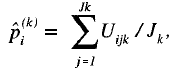
Por último, el error estándar de la estimación para el subgrupo k se calcula con la expresión:
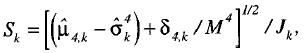
donde
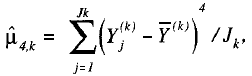
y
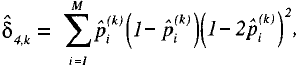
El valor del estadístico T es comparado con la cola superior de la distribución normal estándar para obtener el nivel de significación. Cuanto más grandes sean los valores de p, mayor será el grado de cumplimiento del supuesto de unidimensionalidad esencial; mientras que, la multidimensionalidad se traducirá en valores de p dentro de los niveles de significación especificados.
En resumen, la lógica del estadístico T de Stout está en la comparación de las dos estimaciones de la varianza - usual y unidimensional - entre grupos de personas igualados por sus puntuaciones totales en PT. La estimación unidimensional consiste en la suma de M variables de Bernoulli, suma que supone la independencia de las M-variables (i. e. en este contexto de los M-ítems). Si el modelo que subyace a las respuestas a los ítems es esencialmente unidimensional, los M-ítems de AT1 y AT2 serán localmente independiente de forma aproximada, las estimaciones de las dos varianzas coincidirán, y por tanto, el valor del estadístico T llevará al mantenimiento de la hipótesis nula. Por el contrario, si el modelo no es esencialmente unidimensional, los ítems de AT1 serán dimensionalmente distintos a los AT2 y PT, el valor del estadístico T aumentará y podrá conducir al rechazo de la hipótesis nula.
El comportamiento de DIMTEST ha sido examinado en numeroso estudios. Champlain y Gessaroli (1991) encontraron la mejor ejecución del procedimiento con tests de más de 25 ítems y muestras superiores a 500 personas. Nandakumar y Stout (1993) optimizaron el procedimiento frente a la posibilidad de adivinación y la inclusión de ítems con elevados niveles de discriminación. Además, mostraron su adherencia al nivel nominal de significación incluso con correlaciones entre las dimensiones de 0.7. Nandakumar (1994) comparó la ejecución de DIMTEST frente a la aproximación de Holland y Rosenbaum (1986) y el análisis factorial no lineal (McDonald, 1982). DIMTEST mostró las mejores razones de rechazo de la Ho en conjuntos bidimensionales. Hattie et al (1996) concluyeron que DIMTEST era adecuado para discriminar entre situaciones unidimensionales y aquellas con más de una dimensión. No obstante, alertaron sobre la necesidad de considerar el tipo de modelo utilizado para generar las respuestas -compensatorio o compensatorio parcial-, y los problemas en la elección automática de los ítems para AT1 si se recurre al análisis factorial, por las dificultades conocidas en la estimación de las correlaciones tetracóricas (Ferrando, 1996). Por último, Nandakumar y Yu (1996) han confirmado la naturaleza no-paramétrica del procedimiento al mostrar su robustez frente a diferentes tipos de distribuciones de habilidad no-normales.
La experiencia instruccional
La oportunidad de aprender (ODA) ha sido la variable instruccional tradicionalmente empleada por los psicómetras para obtener información sobre las experiencias instruccionales de las personas. Anderson (1985) definió la ODA como la cantidad de tiempo dedicada a la enseñanza de una tarea. El procedimiento habitual para obtener información sobre la ODA es el juicio de los profesores (Muthén, 1989).
Sin embargo, según algunos autores (Miller y Linn, 1988) la ODA podría ocultar la dinámica de la enseñanza en las aulas. Por esta razón, decidimos sustituir la ODA por otra variable instruccional dicotómica: haber recibido o no una enseñanza dirigida a favorecer la adquisición de un modelo mental relevante sobre un contenido instruccional. Numerosos estudios muestran que, durante el aprendizaje, las personas elaboran representaciones -«modelos mentales»que dirigen su ejecución en tareas de evaluación (Gagné, 1987). Los modelos mentales incluyen información sobre los requisitos de la tarea y cómo realizarla (Gagné y Glaser, 1987). Mayer (1989) detecta los siguientes efectos de la enseñanza dirigida a la adquisición de un modelo mental: (1) mejora el recuerdo de la información conceptual; (2) disminuye la retención literal; y (3) favorece la aportación de soluciones creativas. Las herramientas para esta enseñanza son los diagramas, ejemplos y no-ejemplos adecuados para las tareas que deberán resolver los alumnos.
En definitiva, la manipulación instruccional consiste en realizar una enseñanza dirigida a favorecer la adquisición de un modelo mental para mejorar la ejecución en un conjunto específico de ítems, mediante la adquisición de supuestas «habilidades menores», que pueden facilitar la elección de la respuesta correcta a dichos ítems.
Los efectos de esta enseñanza sobre un grupo de las personas que respondan al test podrían provocar la aparición de «dimensiones menores», que den lugar a la violación del supuesto de «unidimensionalidad esencial» en las respuestas al conjunto del test o en subconjuntos de ítems.
Método
Sujetos y diseño
Participaron 650 personas de ambos sexos. Todas cursaban la asignatura de Psicometría dentro del tercer curso de la Licenciatura de Psicología. El área de contenido utilizada para la experiencia instruccional fue el tema «Análisis numérico de ítems». Las personas fueron asignadas al azar a dos grupos: 325 al Grupo A (GA) y 325 al Grupo B (GB). Los dos grupos recibían la misma estrategia instruccional para la enseñanza del tema en todos sus apartados menos uno. Para este apartado, con el GA se seguía una estrategia dirigida a facilitar la adquisición de un modelo mental; mientras que, con el GB se utilizaba una enseñanza fundamentalmente descriptiva.
Operacionalización de las variables
La operacionalización de las variables se concreta en las unidades de tratamiento y un test de rendimiento. El instrumento de medida fue elaborado por los autores, siguiendo los pasos establecidos en la literatura (Osterlind, 1989).
1) Unidades de tratamiento
Las unidades de tratamiento son dos informes escritos que presentan básicamente la misma información sobre el tema «Análisis numérico de ítems». Ambos informes, recogen los contenidos del tema tal y como aparecen en los manuales de Psicometría más conocidos (Crocker y Algina, 1986; Osterlind, 1989)
Los informes que recibían los dos grupos sólo diferían en el modo de presentación. Estas diferencias se limitan al apartado del tema: «La utilización del índice 'p' en el análisis de ítems», ya que este era el apartado sobre el que se deseaba realizar una estrategia instruccional diferencial (EID). En concreto, en el informe que se entregaba a los sujetos del GA, la presentación, además de hacerse de forma descriptiva, se acompañaba de diagramas (1 diagrama principal y cuatro diagramas parciales), ejemplos y no ejemplos. El diagrama principal representa un modelo que describe la utilización del índice 'p' para analizar la calidad de un item (ver ANEXO 1). Los ejemplos y no-ejemplos interpretan los resultados del índice 'p' para las alternativas de respuesta al item. La interpretación analiza la elección de la respuesta correcta y los distractores. En el GB la presentación de los contenidos era fundamentalmente descriptiva. La secuencia de presentación de los contenidos fue la misma en los dos informes.
La Tabla 1 presenta el esquema del proceso instruccional que reciben los sujetos en el apartado del contenido objeto de una EID.
La elaboración de los informes se rige por la aproximación al diseño instruccional basada en los trabajos sobre el tema (Gagné, Briggs y Wager, 1988; Merrill, Tennyson y Posey, 1992).
2) Test de rendimiento
El test de rendimiento fue elaborado para medir la ejecución de las personas en el tema del «Análisis numérico de ítems». Estaba formado por 37 ítems de elección múltiple con tres alternativas de respuesta. El test contenía 9 ítems diseñados para medir los apartados del contenido objeto de una estrategia instruccional diferencial. Los ítems demandan la interpretación de los resultados del índice 'p' de la forma presentada en los ejemplos y no-ejemplos de las unidades de tratamiento. El número de ítems «dimensionalmente distintos» se ajusta a las recomendaciones expuestas por Nandakumar (1993) para formar el subtest de evaluación uno (AT1), si se utiliza el juicio de expertos.
Procedimiento
El estudio del contenido de los informes y la administración del test de rendimiento, se realizaron en sesiones de grupo. Las personas no conocían los objetivos del estudio. Tras repartir los informes, se pedía a las personas que estudiaran el contenido como «si se estuvieran preparando para un examen...». También se les informaba que después de estudiar el material iban a responder a un test sobre los contenidos estudiados. Después de estudiar el material respondían al test.
Resultados
Hemos dividido la presentación de los resultados en dos apartados en función de los objetivos del estudio: (1) el cumplimiento del supuesto de «unidimensionalidad esencial» en el test de rendimiento; y (2) el examen de la dimensionalidad del conjunto de ítems que miden el apartado objeto de una EID.
( 1 ) La dimensionalidad del test de rendimiento
El estadístico T de Stout (Stout, 1987) examina la hipótesis de que en el conjunto de las respuestas a
todos los ítems del test se cumple el supuesto de «unidimensionalidad esencial». Esta aplicación del programa DIMTEST se realizó con todos los ítems del test, incluido los ítems diseñados para medir el apartado objeto de una EID. Los ítems que forman el subtest AT1 son elegidos automáticamente por el programa DIMTEST a partir de los resultados del análisis factorial.
Los ítems elegidos para formar AT1 no son demasiado fáciles como muestra el test de Wilconson (p = 0.14), y el 90% de las personas de la muestra fueron incluidas en los cálculos.
La Tabla 2 muestra los resultados de la aplicación de estadístico T de Stout a los ítems del test de rendimiento.
Los valores del estadístico tanto en su versión conservadora (T= -0.1116; p= 0.5444), como en la más potente (T= - 0.1634; p = 0.5650), no permiten rechazar la hipótesis nula. La interpretación de estos resultados apunta a que el conjunto de las respuestas a todos los ítems del test cumple el supuesto de «unidimensionalidad esencial».
(2) La dimensionalidad de los ítems objeto de una EID
Los ítems que forman AT1 son los 9 ítems diseñados para medir el apartado en el que los dos grupos habían recibido diferentes estrategias instruccionales. El estadístico T de Stout examina en este caso si el conjunto de las respuestas a estos 9 ítems cumple el supuesto de «unidimensionalidad esencial». Los 9 ítems de AT1 pasaron el test de Wilconson (p= 0.68), siendo utilizados el 96% de las personas en los cálculos.
La Tabla 3 muestra los resultados de la aplicación del estadístico T de Stout.
Los valores del estadístico en su versión conservadora (T= 6.4953; p < 0.001), y en su versión más potente (T= 7.1736; p < 0.001), permiten rechazar la hipótesis nula. La interpretación de estos resultados es que el conjunto de las respuestas a los 9 ítems diseñados para evaluar el rendimiento en el apartado objeto de una EID incumple el supuesto de «unidimensionalidad esencial».
Discusión
El estudio pretendía examinar el efecto de las diferencias en las experiencias instruccionales sobre la dimensionalidad del test de rendimiento. Los resultados permiten concluir que si las diferencias se reducen al modo de presentación de un apartado del área de contenido la «unidimensionalidad esencial» no resulta afectada. Por otra parte, el procedimiento DIMTEST detecta la posible multidimensionalidad del conjunto específico de ítems, que miden el rendimiento en el apartado sometido a las diferentes experiencias instruccionales. Aunque, la situación de estudio es limitada, la explicación de este último resultado puede estar en la aparición de habilidades secundarias que se distribuyen difencialmente entre los grupos, habilidades que influirían en las respuestas a ese conjunto específico de ítems (Padilla, Pérez y González, en prensa).
La implicación de los resultados se debe valorar en dos perspectivas: (1) el cumplimiento del supuesto de «unidimensionalidad esencial» da seguridad a la hora de aplicar procedimientos analíticos basados en la unidimensionalidad, por ejemplo, los métodos estadísticos para detectar ítems con un funcionamiento diferencial; (2) el incumplimiento del supuesto en un subconjunto de los ítems sugiere la investigación del posible FD de dichos ítems, bien de forma individual bien actuando de forma concertada a través del sistema de puntuación del test (Shealy y Stout, 1993).
Los resultados avalan la utilización del procedimiento DIMTEST para identificar conjuntos de ítems para ser analizados con procedimientos estadísticos que determinen su posible funcionamiento diferencial concertado, por ejemplo, el procedimiento SIBTEST (Shealy y Stout, 1993). Mención especial merece su potencialidad para examinar hipótesis sobre la dimensionalidad y el sesgo a partir del juicio de expertos o del análisis subjetivo sobre el contenido de los ítems.
La teoría de la validez es el contexto general para la interpretación de los resultados en los estudios sobre la dimensionalidad de las puntuaciones. No olvidemos que la falta de unidimensionalidad en los resultados del test puede invalidar la interpretación deseada de las puntuaciones, revelando la intervención de otras variables distintas a las que se pretendía medir con el test.
Anderson, L. W. (1985). Opportunity to leam. En T. Husen y T. N. Postlethwaite (Eds.), The international encyclopedia of education. Oxford: Pergamon Press.
Birenbaum, M., y Tatsuoka, K. K. (1982). On the dimensionality of achievement test data. Journal of Educational Measurement, 19, 259-266.
Birenbaum, M., y Tatsuoka, K. K. (1983). The effect of a scoring system based on the algorithm underlying the student's response patterns on the dimensionality of achievement test data of the problems solving type. Journal of Educational Measurement, 20, 17-26.
Camilli, G., y Shepard, L. (1994). Methods for identifying biased test item. Thousand Oaks. CA: Sage Publications, Inc.
Crocker, L., y Algina, J. (1986). Introduction to classical and modern test theory. Rinehart and Winston, New York.
Cuesta, M. (1993). Utilización de modelos logísticos unidimensionales con datos multidimensionales. Tesis doctoral no publicada. Universidad de Oviedo. Oviedo, España.
Cuesta, M., y Muñiz, J. (1994). Utilización de modelos unidimensionales de teoría de respuesta a los ítems con datos multifactoriales. Psicothema, 6, 283-296.
De Champlain, A., y Gessaroli, M. E. (1991, April). Assessing test dimensionality using an index based on nonlinear factor analysis. Paper presented at the Annual Meeting of the American Educational Research Association, Chicago.
Ferrando, P J. (1996). Evaluación de la unidimensionalidad de los ítems mediante análisis factorial. Psicothema, 8, 397-410.
Gagné, R. M. (1987). Instructional Technology: Foundation. Hillsdale, New Jersey: Lawrence Erlbaum Associates, Publishers.
Gagné, R. M., y Glaser, R. (1987). Foundations in learning research. En R. M. Gagné (Ed.) Instructional Technology: Foundation. (pp. 4984). Hillsdale, New Jersey: Lawrence Erlbaum Associates, Publishers.
Gagné, R. M., Briggs, L. J., y Wager, W. (1988). Principles of instructional design. (3ed). New York: Holt, Rinehart y Winston.
Goldstein, H. (1980). Dimensionality, bias, independence and measurement scale problems in latent trait test score models. British Journal of Mathematical and Statistical Psychology, 33, 234-246.
Hambleton, R. K., y Rovinelli, R. J. (1986). Assessing the dimensionality of a set of test items. Applied Psychological Measurement, 10, 287-302.
Hambleton, R. H., y Swaminathan, H. (1985). Item response theory: Principles and applications. Boston: Kluwer-Nijhoff.
Hattie, J., Krakowski, K., Rogers, H. J., y Swaminathan, H. (1996). An assessment of Stout's index of essential unidimensionality. Applied Psychological Measurement, 20, 1-14.
Holland, P. W., y Rosenbaum, P. R. (1986). Conditional association and unidimensionality in monotone latent variable models. Annals of Statistics, 14, 1523-1543.
Lord, F. M. (1980). Applications of item response theory to practical testing problems. Hillsdale. New Jersey: Lawrence Erlbaum Associatest, Publishers.
McDonalsd, R. P. (1982). Linear versus nonlinear models in item response theory. Applied Psychological Measurement, 6, 379-396.
Mayer, R. E. (1989). Models for understanding. Review of Educational Research, 59, 43-64.
Martínez-Cardeñoso, J., Cuesta, M., y Muñiz, J. (1996). Dimensionalidad y función de información de los tests. Psicothema, 8, 215-220.
Merrill, M. D., Tennyson, R. D., y Posey, L. O. (1992). Teaching concepts: An instructional design guide. Englewood Cliffs, New Jersey: Educational Technology Publications, Inc.
Miller, M. D., y Linn, R. L. (1988). Invariance of item characteristic functions with variations in instructional coverage. Journal of Educational Measurement, 25, 205-219.
Muñiz, J., y Cuesta, M. (1993). El problema de la unidimensionalidad en la medición psicológica. En Forns y Anguera (comps.). Aportaciones recientes a la evaluación psicológica. Barcelona. PPU.
Muthén, B. O. (1989). Using item-specific instructional information in achievement modeling. Psychometrika, 385-396.
Nandakumar, R. (1993). Assessing essential unidimensionality of real data. Applied Psychological Measurement, 17, 29-38.
Nandakumar, R. (1994). Assessing dimensionality of a set of item responses. Comparison of different approaches. Journal of Educational Measurement, 31, 17-35.
Nandakumar, R., y Stout, W. F. (1993). Refinement of Stout's procedure for assessing latent trait dimensionality. Journal of Educational Statistics, 18, 41-68.
Nandakumar, R., y Yu, F. (1996). Empirical validation of DIMTEST on nonnormal ability distributions. Journal of Educational Measurement, 33, 355-368.
Osterlind, S. J. (1989). Constructing test items. Norwell. Massachusetts: Kluwer Academic Publishers.
Padilla, J. L., Pérez, C., González, A., y Rojas, A. (1997, Septiembre). La búsqueda de las causas del funcionamiento diferencial del item/sesgo en el item desde la teoría de la validez. Comunicación presentada al simposium Funcionamiento Diferencial de los Item. V Congreso de Metodología de las Ciencias Humanas y Sociales. Sevilla.
Padilla, J. L., Pérez, C., y González, A. (en prensa). Causas de la ejecución diferencial en los ítems de rendimiento. Psicothema.
Roussos, L. A., Stout, W. F., y Marden, J. I. (1993, April). Dimensional and structural analysis of standardized tests using DIMTEST with hierarchical cluster analysis. Paper presented at the Annual Meeting of the National Council on Measurement in Education, Atlanta, GA.
Shealy, R. S., y Stout, W. F. (1993). A modelbases standardization approach that separates true bias/dif from ability differences and detects test bias/dft as well as item bias/dif. Psychometrika, 58, 159-194.
Stout, W. F. (1987). A nonparametric approach for assessing latent trait unidimensionality. Psychometrika, 52, 589-617.
Stout, W. F. (1990). A new item response theory modeling approach with applications to unidimensionality assessment and ability estimation. Psychometrika, 55, 293-325.
Traub, R. E. (1983). A priori considerations in choosing an item response model. En R. K. Hambleton (Ed.). Applications of item response theory. (pp. 57-70). Vancouver. British Columbia: Educational Research Institute of British Columbia.
Aceptado el 17 de febrero de 1998