COMPARISON OF OPTIMAL CUTOFF POINTS FOR SINGLE AND MULTIPLE TESTS IN PERSONNEL SELECTION

Ruth Ben-Yashar, Shmuel Nitzan and Hans J. Vos^*

University of Bar-Jlan (Israel) and ^* University of Twente (Netherlands)

This paper compares the determination of optimal cutoff points for single and multiple tests in the field of personnel selection. Decisional skills of predictor tests composing the multiple test are assumed to be endogenous variables that depend on the cutting points to be set. It is shown how the predictor cutoffs and the collective decision rule are determined dependently by maximizing the multiple test’s common expected utility. Our main result specifies the condition that determines the relationship between the optimal cutoff points for single and multiple tests, given the number of predictor tests, the collective decision rule (aggregation procedure of predictor tests’ recommendations) and the function relating the tests’ decisional skills to the predictor cutoff points. The proposed dichotomous decision-making method is illustrated by an empirical example of selecting trainees by means of the Assessment Center method.

Comparación de puntos de corte óptimos para uno y múltiples tests en selección de personal. En este trabajo se compara el establecimiento de puntos óptimos de corte para uno o varios tests, en el campo de la selección de personal. La capacidad de decisión de los tests predictores, cuando se emplean varios tests, se asumen como variables endógenas que dependen de los puntos de corte que se establecen. Se muestra cómo los puntos de corte y las reglas colectivas de decisión vienen determinadas por la maximización de la utilidad esperada común de los tests múltiples. El principal resultado consiste en especificar la relación entre los puntos de corte óptimos (para tests simples y múltiples), dado el número de tests predictores, la regla de decisión colectiva (recomendaciones sobre el procedimiento para agregar los tests predictores) y la función que relaciona las capacidades de decisión con el punto de corte. El método de toma de decisiones dicotómica se ilustra con un ejemplo empírico de selección de aprendices por medio del método de «Assessment Center».

Over the past few decades, much psychometric research has been aimed at improving the use of educational and psychological tests as means for decision making rather than for estimating ability scores from test performances. Examples of such decisions are admittance of students to a university and personnel selection in industry (e.g., Chuang et al, 1981; Cronbach and Gleser, 1965; De Corte, 1998; Petersen, 1976; Raju et al., 1991; van der Linden and Vos, 1996; Vos, 1997a), pass-fail decisions in education and successfulness of therapies in psychodiagnostics (e.g., Huynh, 1977; Lewis and Sheehan, 1990; Vos, 2001), optimal assignment of students to different instructional treatments in Aptitude Treatment Interaction (ATI) research (e.g., Cronbach and Snow, 1977; van der Linden, 1981; Vos, 1997b), and vocational guidance decisions in which most promising schools or careers must be identified (e.g., van der Linden, 1987). Optimal cutoff points can be found by formalizing each of the above types of elementary test-based decisions as a problem of Bayesian decision making by maximizing its expected utility (e.g., DeGroot, 1970; Lehmann, 1959).

The existing psychological and educational literature discusses how cutoff points can be determined, while there is only one test or one measure which weighs the scores on a number of tests as a composite score, or, for many tests, how the cutoff point on each test can be determined separately. However, no results are reported how in case of a multiple test composed of several tests the cutoff points on each separate test and the collective rule (i.e., aggregation procedure) can be determined dependently. For example, take a predictor-based selection system in which the collective decision rule is that an applicant must pass (n+1)/2 out of n predictor tests, then one must decide on a cutoff point for each separate predictor test.

Therefore, the goal of this paper is to present a model that takes into account the dependence between the cutoff points on a number of predictor tests composing a multiple test and its aggregation process to come to a collective decision in terms of rejecting or admitting an applicant for a job in industrial/organizational (I/O) psychology. In other words, the cutoff points and the aggregation rule will be optimized simultaneously by maximizing the multiple test’s common expected utility.

In essence, personnel selection involves the screening and comparison of applicants by means of valid procedures with the purpose of obtaining the intended quota of supposedly most successful employees (e.g., Cronbach and Gleser, 1965). In selecting the required quota or selection ratio (i.e., fixed proportion of all applicants that can be accepted due to shortage of resources), a mechanism of top-down selection is usually followed by selecting applicants with the highest scores on the (composite) predictor test until the quota is filled. For instance, the well-known Taylor-Russell (1939) tables are based on this formalism.

In addition, top-down selection formalisms have been proposed in personnel selection that are based on the expected average criterion score of the selected applicants (e.g., Boudreau, 1991; Brogden, 1949; Cronbach and Gleser, 1965; De Corte, 1994). In fact, these methods are prevailing in the literature but cannot be employed if future criterion behavior (i.e., job performance) is assumed to be a dichotomous variable, that is, either successful or not (e.g., Raju et al, 1991). In these situations we have to resort to the expected success ratio, that is, the proportion of applicants accepted that will be successful in their future job performance.

Although the existing psychology literature dealing with classification procedures in terms of acceptance/rejection usually takes the given quota into account, this approach is not followed in the present paper. The main reason is that there are many problems in which it is not feasible to assume quota restrictions, for example, deciding on whether or not to hospitalize a patient. In the field of personnel selection, also situations may exist in which it is not feasible to impose quota restrictions. For instance, if we want to select all applicants who showed satisfactory performance on a fixed number of predictor tests. This is exactly the situation where the present paper is aiming at by selecting all applicants with scores on each predictor test higher than a cutoff point that clearly depends on the number of predictor tests composing the multiple test, the aggregation process of predictor tests’ recommendations, and the function relating the tests’ decisional skills to the cutoff point. In principle, unlike the fixed quota methods, none or all of the applicants might be selected with the unconstrained dichotomous choice model proposed in the present paper.

The problem addressed in the present paper shows some correspondence to the case of multiple hurdles or multi-stage selection in I/O psychology (e.g., De Corte, 1998, Milkovich and Boudreau, 1997; Sackett and Roth, 1996). The case of multiple hurdles deals with a situation in which an applicant is expected to show minimum proficiency in several skill areas. In this scenario, as opposed to, for instance, multiple regression analysis, a high proficiency in one skill area will not typically compensate for a low proficiency in another skill area.

The model advocated here has been applied earlier successfully by Ben-Yashar and Nitzan (1997, 1998, 2001) to the field of economics where organizations face the comparable problem of deciding on approval or rejection of investment projects. A team of n decision makers has to decide which ones of a set of projects are to be accepted so as to maximize the team’s common expected utility. The proposed group decision-making method can be applied to many binary decisions determined by teams of decision makers or test systems.

The paper is organized as follows. Section 2 applies the Ben-Yashar and Nitzan economic model to the field of personnel selection. In Section 3 we derive necessary and sufficient conditions for optimal cutoff points of single and multiple tests. In Section 4 the optimal cutoff points set on single and multiple tests are compared by deriving an inequality that specifies the relationship between these two types of cutoff points. Section 5 focuses on the comparison of the two types of cutoff points for special types of collective rules, namely, disjunctive and conjunctive ones. The comparison between optimal cutoff points for single and multiple tests in predictor-based selection is empirically illustrated in Section 6 where applicants are either accepted or rejected as trainees by means of the Assessment Center method. The concluding section contains a brief summary of the main result and discusses a possible line of future research arising from the present study.

The model

In the field of personnel selection, it often occurs that an applicant is either accepted or rejected for a job based on a multiple test composed of several predictor tests, i.e., a battery of n (n ≥ 1) performance measures such as psychological tests, role-plays, and work sample tasks. It is assumed that the true state of an applicant regarding the future job performance (usually a supervisory performance rating) is unknown and can be qualified as either suitable (s= 1) or unsuitable (s= -1). An applicant is qualified as suitable if his or her performance is at least equal to a pre-established cutoff point (performance level) on the criterion variable(s) represented by the future job performance. Furthermore, based on applicant’s performance on predictor test i (1 ≤ i ≤ n), it is decided if an applicant is passed (a_i= 1) or failed (a_i= -1) on predictor test i. The predictor tests i will usually differ in their outcomes regarding passing or failing of applicants. The decision table for each predictor test i is therefore:

The true state of an applicant, however, is unknown on each of the n predictor tests. Instead, an applicant receives a test score x_i (i.e., a performance rating) on each predictor test i which depends on applicant’s performance in a certain skill area. It is assumed that the scales of the predictor tests have been transformed such that they cover all the same range of test scores. The pass-fail decision a_i is now made by setting a cutoff point on each test score x_i in the form of a threshold R_i (i.e., predictor cutoff) such that

The test score x_i is drawn from a known distribution function represented by the density f₁(x_i) for suitable and f₂(x_i) for unsuitable applicants. Therefore, the conditional probabilities p¹_i and p²_i that a predictor test i makes a correct pass-fail decision under the two possible states of nature (the decisional skills of each predictor test) are:

and

where (1-p¹_i) and (1-p²_i) can be interpreted as Type I and Type II error probabilities (i.e., probabilities of making incorrect fail and pass decisions) of each predictor test i. Decisional skills of predictor tests are assumed to be endogenous variables that depend on the cutoff points to be set.

Note that we make the following assumptions: (i)

This assumption implies that p¹_i>(1-p²_i), that is, a suitable applicant is more likely to be passed on predictor test i than an unsuitable applicant. Thus, since the simple average of the test’s decisional skills in the two states of nature exceeds 0.5, each predictor test participating in the collective decision-making process is valuable because this test’s decisional skill is superior to that of a random decision process. (ii) decisional skills of predictor tests are statistically independent. It should be noted that the assumption of statistical or local independence is also frequently made in other applications of psychological and educational tests. Local independence then means that when the abilities influencing test performance are held constant (i.e., conditioning on ability), examinees’ responses to any pair of items are statistically independent. In fact, local independence is one of the basic assumptions made in Item Response Theory (IRT) models (e.g., Hambleton et al, 1991; Olea et al, 2004).

The vector a = (a₁,…, a_n) is referred to as the decision profile of a set of n predictor tests for an individual applicant, where a_i= 1 or a_i = -1 denotes if the applicant is either passed or failed on predictor test i (1 ≤ i ≤ n). The collective decision, acceptance (1) or rejection (-1) of an applicant, is then determined by means of a decisive aggregation rule g that transforms the profile of decisions on n predictor tests into a collective decision. g is referred to as the structure of the collective decision-making process and assigns 1 or –1 (acceptance or rejection of an applicant) to any decision profile a in Ω= {1,-1}ⁿ. That is, g: W Æ {1,-1}. The same problem is faced in the multiple hurdles scenario where, based on applicant’s performance on several tests, a collective decision 1 or –1 (acceptance or rejection of an applicant) must be made.

To formally define the objective function (i.e., the multiple test’s common expected utility), we need to present the conditional probabilities of reaching a correct collective decision, given the structure g. Let us therefore partition the set Ω of all decision profiles into A(g/1) and A(g/-1), where A(g/1)= {a Œ ω Ág(a)= 1} and A(g/-1) = {a Œ Ω Ág(a)= -1}, where g(a) is the collective decision for a decision profile a. For a given structure g, the collective decision-making process accepts a suitable applicant and rejects an unsuitable applicant with probability ψ(g/1) and ψ(g/-1), respectively, where ψ(g/1)= Pr{a Œ A(g/1) Ás= 1} and j(g/-1)= Pr{a Œ A(g/-1) Ás= -1}. Note that for a single test i, ψ(g/1) and ψ(g/-1) are equal to respectively p¹_i and p²_i.

Necessary and sufficient conditions for optimal cutoff points

For a multiple test, our goal is to derive the collective decision rule g and cutoff point R_i (1 ≤ i ≤ n) on predictor test i (1 ≤ i ≤ n) dependently that maximize the multiple test’s common expected utility. Therefore, the following problem is faced:

where U(1/1), U(1/-1), U(-1/-1) and U(-1/1) are the (economic) utilities corresponding to the four possible decision outcomes on each predictor test, that is, correct passing (true positive), incorrect passing (false positive), correct failing (true negative), and incorrect failing (false negative). Furthermore, α (α 0,1) and (1-a) denote the a priori probabilities that an applicant is qualified as either suitable (1) or unsuitable (-1). Since [αU(-1/1) + (1-α)U(1/-1)] does not depend on R_i, the above maximization problem can be reduced to the following form:

Let U(1)= [U(1/1) - U(-1/1)] denote the positive net utility corresponding to the correct pass decision, and let U(-1)= [U(-1/-1) - U(1/-1)] denote the positive net utility corresponding to the correct fail decision, it then follows that the maximization problem in (1) can be formulated as:

Note that the optimal decision-making method for a multiple test consists of a collective decision rule g and a vector of optimal predictor cutoff values.

Threshold utility

It should be mentioned that in fact a so-called threshold utility function is assumed in the present paper. That is, the utilities involved can be summarized by possibly different constants for each of the four possible decision outcomes (i.e., fixed utilities). In other words, although the utilities depend indirectly on the value of the predictor cutoff R_i via the pass-fail decision, they do not explicitly depend on R_i. For instance, the utility corresponding to an incorrect pass decision on predictor test i (i.e., U(1/-1)) for an unsuitable applicant who is far above R_i is the same as for an incorrect pass decision for an unsuitable applicant who is performing just above R_i. This will be true for both suitable applicants and unsuitable ones. Considering the joint distribution of the applicant predictor and criterion scores, it is also obvious that the expected criterion score (and hence, the utility) of an applicant who passed predictor test i will vary for different cutoff values of R_i. Most current models of personnel selection utility, therefore, follow the classical Brogden-Cronbach-Gleser suggestion (Brogden, 1949; Cronbach and Gleser, 1965) to express the utility explicitly as a function of the predictor cutoff R_i.

However, like the model proposed in this paper, some models of personnel selection utility assume that utility does not explicitly depend on the value of R_i by adopting a threshold utility function (e.g., Chuang et al, 1981; Petersen, 1976; Raju et al, 1991; Vos, 2001). Threshold utilities are also frequently assumed as being appropriate in the context of educational decision making (e.g., Huynh, 1977; Lewis and Sheehan, 1990; van der Linden, 1987). The main reason for defending threshold utility by all these authors is that, referring to the previous given example, applicants with scores on predictor test i far above R_i will hardly never be qualified as unsuitable. Moreover, these authors assume that utilities corresponding to the correct pass and fail decisions (i.e., U(1/1) and U(-1/-1)) remain relatively stable for applicants with predictor scores respectively far above and far below R_i. So, if it is assumed that utilities are in fact only sensitive to changes in predictor scores around the cutoff point R_i, the discontinuous threshold function as a «jump» from one constant value to another can be defended as a realistic model for personnel selection utility.

Finally, it can still be remarked that threshold utilities are quite convenient from a mathematical point of view. As will become clear below, not the absolute utilities U(1/1), U(-1/1), U(-1/-1) and U(1/-1) have to be specified for computing the optimal cutoff points but only the so-called utility ratio U(1)/U(-1), that is, U(1) relative to U(-1), has to be specified.

Most texts on decision theory propose lottery methods for empirically assessing the fixed values of the threshold utility function (and hence, the utility ratio (e.g., Luce and Raiffa, 1957)). Generally speaking, these methods use the desirability of outcomes to scale the consequences of each pair of decision outcome and true state. In the empirical example below, the correct and incorrect pass decisions were perceived as respectively the most and the least preferred outcomes from the economic perspective of the company (e.g., hiring and training costs).

Qualified majority rule (QMR)

Quite often the collective decision rule g is given and not necessarily optimal. However, it might still be possible to improve the predictor-based selection process by controlling its optimal cutoff point R^*_i on each predictor test i (1 ≤ i ≤ n). Suppose now that a qualified majority rule (QMR) is employed, which is defined as follows:

where N(-1) is the number of predictor tests failed by the applicant, n is the number of predictor tests, and k (1/n ≤ k ≤ 1 and kn is an integer) is the minimal proportion of predictor tests failed by the applicant necessary for the collective decision to be -1 (rejection of applicant). The parameter k represents the collective decision rule g, or the structure of the decision-making process. For instance, a simple majority rule k= n+1/2n implies that an applicant is rejected if N(-1)≥ n+1/2 and accepted otherwise. It should be noticed that the assumption of a QMR is plausible because the optimal collective decision rule is always a qualified majority one, as shown in Ben-Yashar and Nitzan (1997). The problem we face is therefore:

Given the structure k of collective decision-making and the number n of predictor tests, the optimal cutoff point R^*_i on predictor test i (1 ≤ i ≤ n) of a multiple test is determined by the following necessary condition:

where,

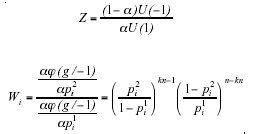
The proof of the above assertion is given in Ben-Yashar and Nitzan (1998).

In a single test i, it obviously holds that n, and thus k, is equal to 1 implying that W_i= 1. It follows then immediately from (3) that the optimal cutoff point R⁺_i on predictor test i (1 ≤ i ≤ n) in this case is determined by the following necessary condition:

Note that (4) also follows immediately from (2) since ψ(g/1)= p¹_i and ψ(g/-1)= p²_i for a single test i (1 ≤ i ≤ n).

The term Z which appears in equations (3) and (4) relates to the environmental characteristics of the decision-making process, viz., the prior that an applicant is suitable and the fixed utilities corresponding to the four possible outcomes for a predictor test. In fact, Z represents the quality of the selection environment. If state of nature 1 is superior to state of nature -1, the lower the Z, the higher the quality of this environment. Z < 1 represents an environment of relatively high quality. Z > 1 represents a relatively low-quality environment. Z = 1 represents a neutral environment. In other words, in this case there is no bias in favor of acceptance-rejection and pass-fail decisions of applicants in terms of respectively the priors of the two states of nature (i.e., α= (1-α)) and the net utilities corresponding to the two states of nature (i.e., U(1)= U(-1)).

The term W_i which appears in (3) and not in (4) is the ratio between the marginal contribution of a test’s decisional skill to the collective probability of making a correct decision in states of natures –1 and 1. W_i depends on the three characteristics of the decision-making process: structure (collective decision rule), number of predictor tests composing a multiple test and a performance measure of its predictor tests which depends on their decisional skills. Note that when W_i= 1 the effect of a marginal change in a test’s decisional skill is identical under the two states of nature, that is,

Relationship between optimal cutoff points for single and multiple tests

The optimal cutoff points for single and multiple tests in predictor-based selection are usually different. Whether or not the cutoff points for single tests are stricter than the cutoff points for multiple tests depend on the characteristics of the decision-making setting: the preferred decisional skills of the predictor tests, the number of predictor tests and the collective decision rule. Our main result specifies the condition that determines the relationship between the optimal cutoff points R⁺_i and R^*_i for single and multiple tests in predictor-based selection.

Theorem 1:

where

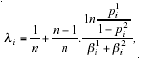
n is the fixed size of the number of predictor tests,

The parameter λ_i (1 ≤ i ≤ n) can be interpreted as the bias/asymmetry of the tests’ decisional skills.

For the proof of this theorem, we refer to Ben-Yashar and Nitzan (2001).

The relationship between R^*_i and R⁺_i depends on the relationship between and that depends on k. When , i.e., when W_i > 1, from the perspective of a multiple test there exists a relative advantage to an increase in tests’ decisional skills in state of nature –1. This induces an increase in p²_i and a decrease in p¹_i by setting the cutoff point R^*_i higher than R⁺_i (recall that ).

A similar argument can be used to rationalize the determination of R^*_i which is lower than R⁺_i when W_i < 1.

Alternatively, the relationship between R^*_i and R⁺_i depends on the relationship between k and lambda;_i. When k > λ_i, i.e., the structure of the multiple test is sufficiently lenient toward acceptance of applicants, the decision-making system reacts by setting a cutoff point higher than the one set on a single test i, namely, by setting R^*_i which exceeds R⁺_i. A similar argument can be used to rationalize the inequality R^*_i < R⁺_i when k < l_i. Notice that the difference between R^*_i and R⁺_i is basically due to the interchangeability between R_i and k (Ben-Yashar and Nitzan, 1998).

To further clarify the intuition behind the theorem from a personnel selection perspective and, in particular, why , let us first show that in a neutral environment λ_i approximates the optimal QMR for a multiple test consisting of a large number of predictor tests. In a neutral environment where Z= 1, the optimal QMR for predictor test i (1 ≤ i ≤ n) of a multiple test, k^*_i, is given by:

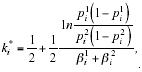
which follows immediately from the optimal QMR in the general case that Z represents a bias/asymmetry in the environmental characteristics of the decision-making process (i.e., Z=1):

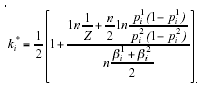(5)

Ben-Yashar and Nitzan (1997) provides a proof of the above assertion. Notice that

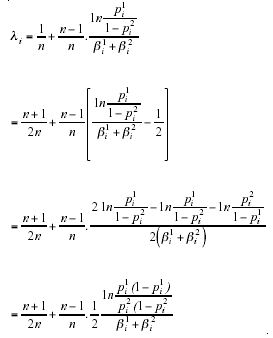
which converges to k^*_i for a sufficiently large n. When p¹_i = p²_i, λ_i = 0.5; that is, the optimal QMR for predictor test i (1 £ i £ n) of the multiple test is the simple majority rule.

When p¹_i < p²_i, l_i > 0.5; that is, the optimal QMR favours the acceptance of applicants which is less likely to be the correct decision. If the given collective decision rule, k, implies a bias that optimally takes into account the difference between p¹_i and p²_i, i.e., k= l_i, then from the perspective of a multiple test there is no incentive to set R_i and, in turn, p¹_i and p²_i that differ from those set in a single test. In such a case R^*_i = R⁺_i. If a collective decision rule k is faced that implies a bias in favour of selection of applicants which is stronger than the optimal bias corresponding to p¹_i and p²_i, i.e., k > λ_i, then an incentive exists to adjust p¹_i and p²_i in order to eliminate the discrepancy between k and λ_i. The adjustment requires an increase of R_i which reduces p¹_i and raises p²_i, and therefore in such a case R^*_i > R⁺_i. A similar argument can be used for the case k < λ_i, which completes our intuitive explanation why

Disjunctive and conjunctive rules

A number of implications can be obtained from Theorem 1 in special cases of our model, that is, when specific assumptions are made regarding n, k, and the relationship between the endogenous decisional skills of predictor tests, p¹_i and p²_i.

As already noted, the structure of the decision-making system is represented by k, the minimal proportion of predictor tests in favour of alternative -1 (fail decision), necessary for the collective decision to be -1 (rejection of applicant). The following discussion, however, pertains to the structure of the decision-making system necessary for collectively reaching the decision 1 (acceptance of applicant). Hence kn= n means that the collective rule is a disjunctive one (or polyarchic rule). That is, if one predictor test decides in favour of alternative 1 (pass decision), then the collective decision is 1 (acceptance). kn= 1 means that the collective rule is a conjunctive one (or hierarchic rule). That is, the collective decision is 1 (acceptance) only when an applicant is passed on all predictor tests. In fact, a conjunctive test can be interpreted as a case of multiple hurdles in personnel psychology.

By assumption, p¹_i > (1-p²_i). Hence, for a conjunctive rule where kn= 1,

By Theorem 1, in such a case R^*_i < R⁺_i. In the extreme case of a disjunctive rule where kn= n, and using p_i² > and by Theorem 1, R^*_i > R⁺_i.

The determination of optimal cutoff points for multiple tests takes into account the collective decision rule, k, and the interchangeability between k and the cutoff point R_i. No wonder then that for a disjunctive rule where the collective decision rule is most lenient toward acceptance of applicants, stricter cutoff points are set relative to the cutoff points set on single tests. In contrast, for a conjunctive rule, where the collective decision rule is least lenient toward acceptance of applicants, more tolerant cutoff points are set relative to the cutoff points set on single tests.

In the symmetric case where there is no bias in favor of acceptance-rejection and pass-fail decisions of applicants both in terms of the collective decision rule, , and in terms of the predictor cutoff which results in p¹_i = p²_i, the same cutoff points are set on single and multiple tests. Formally, since

, we obtain that if a simple majority rule is applied, that is, if and the cutoff point yields identical decisional skills of the predictor tests, p¹_i = p²_i, as frequently assumed in the literature, then W_i= 1 and λ_i= n+1 /2n=k .

By Theorem l, in such a case R^*_i = R⁺_i.

Finally, suppose that [αU(1) = (1-α)U(-1)]. In this symmetric situation (i.e., Z= 1), the optimal cutoff point R⁺_i on the single test is set by maximizing its expected utility [αU(1)p¹_i + (1-α)U(-1)p²_i] implying that its average decisional skill is maximized as well. In general, R⁺_i differs from R^*_i. However, regardless of whether R^*_i > R⁺_i or R^*_i < R⁺_i, in this symmetric situation there is always a tendency that the average decisional skills of the predictor tests of a multiple test are reduced relative to the average decisional skills of a single test.

Predictor-based selection using the Assessment Center method: an illustration

To illustrate Theorem 1 for comparing the optimal cutoff points R⁺_i and R^*_i set on single and multiple tests, the Assessment Center (AC) method is given as an empirical example. The term refers to a procedure for evaluating the performance of individuals for such purposes as selection or promotion of employees (e.g., Roos et al, 1997). In a typical Assessment Center the candidates applying for a job participate in a variety of exercises that enable them to demonstrate a particular (interpersonal) skill, knowledge, ability, or competence, usually called job dimensions. These dimensions resemble the future professional practice as much as possible. The performance rating on each exercise is done by observers (called assessors) who are carefully trained in order for the method to be valid and reliable. Comparing these ratings with a pre-established cutoff point, it is decided whether or not an applicant’s performance on each specific exercise is satisfactorily enough to be passed. Then the assessors combine the pass-fail decisions on all the exercises and reach a collective decision (i.e., aggregation procedure) for each applicant, that is, either accept or reject the applicant for the job.

In the current example, data were available for a large company. The candidates applying for trainee positions in this company spent two days undergoing assessment of their managerial potential by the Assessment Center method. The following 15 exercises were identified: Oral communication, planning and organization, written communication, analysis, reading skills, judgment, initiative, sensitivity, leadership, management identification, delegation, technical knowledge, reflection, trouble shooting, and presentation. The performance on each of the 15 exercises (i.e., the predictor tests i) of the Assessment Center (i.e., the multiple test) was rated by one and the same team of two carefully trained assessors on a 100-point scale running from 0 to 100. So, i was running from 1 to 15 and each predictor score x_i was running from 0 to 100.

Since the company did not have any prior information of the applicants, the a priori probabilities a and (1-a) of qualifying an applicant’s true state (i.e., future job behavior) as respectively suitable (s= 1) or unsuitable (s= -1) were set equal. Hence, α= (1->α)= 0.5.

Furthermore, using the lottery method described in Luce and Raiffa (1957), the positive net utility corresponding to a correct pass decision (i.e., U(1)) was perceived by the company from an economic perspective twice as large as the positive net utility corresponding to a correct fail decision (i.e., U(-1)). Hence, since the utility ratio U(1)/U(-1)= 2 and α= (1-α)= 0.5, it follows that Z= 1/2. Since Z < 1, we are thus dealing with environmental characteristics of the Assessment Center that can be characterized as being of relatively high quality.

In order to calculate the optimal cutoff point R^*_i on each single exercise i (1 ≤ i ≤ 15) of the Assessment Center by means of (3), given the collective decision rule k and number n of exercises, we finally still need to specify p¹_i and p²_i as functions of R_i. It was assumed that the test score distributions f₁(x_i) and f₂(x_i) for exercise i (1 ≤ i ≤ 15) in the suitable and unsuitable group of applicants followed the normal distribution with mean µ¹_i and µ²_i (with µ²_i lower than µ¹_i) and standard deviation σ¹_i and σ²_i, respectively. Based on a sample of 127 candidates (69 accepted and 58 rejected) applying for trainee positions in the past, it will first be described how it was determined if an applicant was qualified as either suitable (σ= 1) or unsuitable (s= -1). Using this information, the parameters µ¹_i, µ²_i, s¹_i and s²_i (1 ≤ i ≤ 15) can be estimated straightforward.

First, depending on applicant’s performance, for each applicant (both accepted and rejected ones) a test score x_i (0 ≤ x_i ≤ 100) was assigned to each exercise i (1 ≤ i ≤ 15) by the team of two assessors. Henceforth, the predictor score on exercise i will be denoted as X_i. Next, for each selected applicant a criterion score y_i (i.e., applicant’s supervisor rating of current job performance concerning exercise i on a 100-point scale) was determined on the criterion variable Y_i (1 ≤ i ≤ 15). Future job performance will be denoted as the composite criterion variable Y. For the group of selected applicants the following statistics could now be computed for each exercise i (1 ≤ i ≤ 15): the means µ_Xi and µ_Yi, the standard deviations σ_Xi and σ_Yi, and the correlation r_XiYi (i.e., validity coefficient) between X_i and Y_i. Using these statistics, we then computed for each rejected applicant the predicted criterion score yˆ_i (i.e., future job behaviour on exercise i if the applicant would have been selected) as a linear regression estimate on applicant’s predictor score x_i:

Note that Brogden’s utility model (1949) also assumed the above linear regression estimate for a single employee in which yˆ_i then stands for the dollar value of an employee’s performance on exercise i.

Next, for each applicant (both accepted and rejected ones), a composite criterion score y on Y was calculated by taking his or her average criterion score over all 15 exercises. Finally, each applicant was qualified as either suitable (s= 1) or unsuitable (s= -1) by examining if applicant’s composite criterion score y was above or below a pre-established cutoff point y_c= 55 on the criterion variable Y. The mean and standard deviation of f₁(x_i) and f₂(x_i) could now be estimated straightforward for each exercise i (1 ≤ i ≤ 15).

The comparison of the optimal cutoff points R⁺_i and R^*_i set on single and multiple tests by using Theorem 1 will be illustrated for the 9th exercise of leadership (i.e., i= 9). It should be emphasized, however, that the calculation of the optimal cutoff points R⁺_i and R^*_i (and thus their comparison by using Theorem 1) for the other 14 exercises proceeds exactly in the same way. The parameters of f₁(x₉) and f₂(x₉) were estimated as follows: µ¹₉= 74.12, µ²₉= 50.68, s¹₉= 10.79, and µ²₉= 11.66. The assumption of normality for f₁(x₉) and f₂(x₉) was tested using a Kolmogorov-Smirnov goodness-of-fit test. It turned out that the probabilities of exceedance were respectively 0.289 and 0.254, showing a satisfactory fit (significance level of 0.05) against the data.

Thus, using the customary notation F(µ,s) for the normal distribution with mean µ and standard deviation s, the cumulative density is φ(µ¹₉,σ¹₉) for the suitable and φ(µ²₉,σ²₉) for the unsuitable applicants on Exercise 9. It then follows that p¹₉= 1–φ((R₉–µ¹₉/s¹₉) (where φ((R₉–µ¹₉/σ¹₉) now represents the lower tail probability of the standard normal distribution evaluated at the cutoff point R₉), whereas p²₉= φ((R₉–µ²₉/σ²₉).

Relation between R^*₉ and R⁺₉ for given values of k and n

R⁺₉ was computed by inserting , into (4) resulting in R⁺₉= 58.77. R⁺₉ was computed numerically using a root finding procedure from the software package Mathematica (Wolfram, 1996).

In order to investigate the influence of more and less lenient collective rules on the optimal predictor cutoff, R^*₉ was computed for k= 3/15, k= 8/15, and k= 13/15. Inserting first k= 3/15 and n= 15 into W₉ and next W₉ and Z = 0.5 into (3), and using again the root finding procedure from Mathematica (Wolfram, 1996), resulted in R^*₉= 51.04, W₉= 0.219, l₉= 0.224, p¹₉= 0.984, and p²₉= 0.512. So, verifying Theorem 1 for k= 3/15 = 0.2 results in:

As can be seen from the above result, R^*₉ < R⁺₉ implying that a more tolerant cutoff point is set on Exercise 9 of the multiple test composed of 15 exercises relative to the cutoff point set on the single Exercise 9. This result can be accounted for that the collective rule k = 3/15 is much less lenient toward selection of applicants than the simple majority rule since kn = 3 < 8 (i.e., (15+1)/2). This ‘conjunctive like’ character of the collective rule k= 0.2 also implies that p¹₉ is so large (and thus, p²₉ so low) due to only selecting applicants from which we can be pretty sure that they will be qualified as suitable in their future job performance.

Observe that Type I error (i.e., 1-p¹₉= 0.016) is smaller than Type II error (i.e., 1-p²₉= 0.448). This result is desirable from an economic perspective of the company since the probability of selecting applicants who turn out to be unsuitable in their future job performance should be lower than the probability of rejecting applicants who would have been suitable in their future job performance.

Next, for k= 8/15 = 0.533 (i.e., the simple majority rule), we obtained the following results: R^*₉= 62.43, W₉= 1.995, λ₉= 0.520, p¹₉= 0.861, and p²₉= 0.843. According to Theorem 1, a somewhat stricter cutoff point R^*₉ is now set on Exercise 9 of the multiple test composed of 15 exercises relative to the cutoff point R⁺₉ set on the single Exercise 9. This makes sense since the simple majority rule is more lenient toward selection of applicants than the collective rule k = 3/15. As a consequence of the more lenient character of the simple majority rule, p¹₉ and p²₉ were respectively decreased and increased on Exercise 9 relative to the collective rule k = 3/15. It can easily be verified that the simple majority rule meets the requirement formulated in (6) for Exercise 9, since W₉= 1.995 > 1 € p¹₉= 0.861 > p²₉ = 0.843.

Finally, for k= 13/15 = 0.867, we obtained the following results: R^*₉= 73.36, W₉= 14.31, λ₉= 0.819, p¹₉= 0.528, and p²₉= 0.974. As can be verified from Theorem 1 (i.e., W₉ >> 1), a much stricter cutoff point R^*₉ is now set on Exercise 9 of the multiple test composed of 15 exercises relative to the cutoff point R⁺₉ set on the single Exercise 9. This is because the collective rule k= 13/15 is much more lenient toward selection of applicants than the simple majority rule. This ‘disjunctive like’ character of the collective rule k= 13/15 also accounts for the finding that p²₉ is so large (and thus, p¹₉ so low) since we only reject applicants from which we can be pretty sure that they would be qualified as unsuitable in their future job performance.

As an aside, it may be noted that the requirements of W₉ < 1 and W₉ > 1 for respectively a conjunctive and disjunctive rule were met since W₉= 0.032 for k= 1/15 (conjunctive rule) and W₉= 54.76 for k= 1 (disjunctive rule). Notice also that the assumption of p¹₉ > (1-p²₉) is satisfied in all of the above values for k, implying that a suitable applicant is more likely to be passed on Exercise 9 than an unsuitable applicant.

Relation between R^*₉ and R⁺₉ for given value of n= 15

R^*₉ and k^*₉ will be determined dependently for Exercise 9 and given value of n = 15 by maximizing simultaneously the multiple test’s common expected utility and subsequently comparing R^*₉ with R⁺₉ again. First k₉ is written as function of R₉ according to (5), then this function is inserted into (3) and solved for R^*₉. In doing so, according to the definition of a QMR, k₉n must be rounded off to the next highest integer. Using again a root finding procedure from the software package Mathematica (Wolfram, 1996), yielded the following results: R^*₉= 60.47, k^*₉= 7/15 = 0.467, W₉= 1.380, l₉= 0.461, p¹₉= 0.897, and p²₉= 0.799. As is clear from Theorem 1, a somewhat stricter cutoff point R^*₉ is now set on Exercise 9 of the multiple test composed of 15 exercises relative to the cutoff point R⁺₉= 58.77 set on the single Exercise 9. Note that the optimal collective rule for Exercise 9 is only one exercise more lenient toward selection of applicants than the simple majority rule; that is, 9 out of 15 versus 8 out of 15 exercises must be passed at least for being accepted, respectively.

Using the optimal value of k^*₉= 7/15 for Exercise 9, the optimal predictor cutoffs R^*_i may now be calculated on the other 14 exercises of the multiple test (i.e., 1 ≤ i ≤ 15; i π 9) using (3) again. This makes sense when one wants to be sure that anycase for Exercise 9, the predictor cutoff and QMR are optimized simultaneously. For instance, because Exercise 9 is perceived as the most important exercise of the multiple test.

Conclusions

This paper focuses on the comparison between the optimal cutoff points set on single and multiple tests in predictor-based selection. Since the characteristics of the two types of tests differ, these cutoff points are usually different. The relationship between them depends on the number of predictor tests composing a multiple test, on its collective decision rule, and on the tests’ decisional skills. Our main result implies that the cutoff point for a multiple test is stricter than the cutoff point set on a single test, if the collective decision rule is sufficiently lenient toward acceptance of candidates applying for a job, as in the extreme case of a disjunctive rule. More generally, the structure of the decision-making process applies stricter cutoff points for selection of applicants if the marginal contribution of a test’s decisional skill to the collective probability of rejecting unsuitable applicants is larger than its marginal contribution to the collective probability of accepting suitable applicants.

Our results are applied to compare the predictor cutoffs adopted in centralized selection systems and less informed decentralized selection systems. Clearly, decentralized predictor-based decision making in selection systems based on incomplete information can be improved. This is illustrated in the context of collective decision-making using the Assessment Center method by a team of assessors regarding the acceptance or rejection of candidates applying for trainee positions in a large company.

A possible line of future research would be, following the classical Brogden-Cronbach-Gleser suggestion (Brogden, 1949; Cronbach and Gleser, 1965), to express the utility function rather as a function of the predictor cutoff R_i than as a threshold utility like in the present paper. For instance, analogous to Brogden’s pioneering utility equation (1949), by expressing the utility for a single employee (i.e., the observed dollar value of an employee’s job performance) as a linear regression on the score of predictor test i (see also (7)). The choice of this utility function would be more in line with current models of personnel selection utility.

Acknowledgements

The authors are indebted to Saskia Klomp for providing the data for the empirical example and to Wim M.M. Tielen for his computational support.

Ben-Yashar, R. and Nitzan, S. (1997). The optimal decision rule for fixed size committees in dichotomous choice situations: the general result. International Economic Review, 38(1), 175-187.

Ben-Yashar, R. and Nitzan, S. (1998). Quality and structure of organizational decision making. Journal of Economic Behavior and Organization, 36, 521-534.

Ben-Yashar, R. and Nitzan, S. (2001). Investment criteria in single and multi-member economic organizations. Public Choice, 109, 1-13.

Boudreau, J.W. (1991). Utility analysis for decisions in human resource management. In M.D. Dunette and L.M. Hough (eds.): Handbook of industrial and organizational psychology (vol. 2, 2nd ed., pp. 621-745). Palo Alto, CA: Consulting Psychologists Press.

Brogden, H. (1949). When testing pays off. Personnel Psychology, 2, 171-183.

Chuang, D.T., Chen, J.J. and Novick, M.R. (1981). Theory and practice for the use of cut-scores for personnel decisions. Journal of Educational Statistics, 6, 129-152.

Cronbach, L.J. and Gleser, G.L. (1965). Psychological tests and personnel decisions (2nd ed.). Urbana, Ill.: University of Illinois Press.

Cronbach, L.J. and Snow, R.E. (1977). Aptitudes and instructional methods: a handbook forresearch on interactions. New York: Irvington Publishers, Inc.

De Corte, W. (1994). Utility analysis for the one-cohort selection decision with a probationary period. Journal of Applied Psychology, 79, 402-411.

De Corte, W. (1998). Estimating and maximizing the utility of sequential selection decisions with a probationary period. British Journal of Mathematical and Statistical Psychology, 51, 101-121.

DeGroot, M.H. (1970). Optimal statistical decisions. New York: McGraw-Hill.

Hambleton, R.K., Swaminathan, H. and Rogers, H.J. (1991). Fundamentals of item response theory. Newbury Park, CA: Sage.

Huynh, H. (1977). Two simple classes of mastery scores based on the beta-binomial model. Psychometrika, 42, 601-608.

Lehmann, E.L. (1959). Testing statistical hypotheses (3rd ed.). New York: Macmillan.

Lewis, C. and Sheehan, K. (1990). Using Bayesian decision theory to design a computerized mastery test. Applied Psychological Measurement, 14, 367-386.

Luce, R.D. and Raiffa, H. (1957). Games and decisions. New York: John Wiley and Sons.

Milkovich, G.T. and Boudreau, J.W. (1997). Human resource management (8th ed.). Chicago, IL: Richard D. Irwin.

Olea, J., Abad, J., Ponsoda, V. and Ximénez, M.C. (2004). A computer adaptive test for the assessment of written English. Psicothema, 16(3), 519-525.

Petersen, N.S. (1976). An expected utility model for ‘optimal’ selection. Journal of Educational Statistics, 4, 333-358.

Raju, N.S., Steinhaus, S.D., Edwards, J.E. and Lehessio, J. (1991). A logistic regression model for personnel selection. Applied Psychological Measurement, 15, 139-152.

Roos, J., Roos, G., Dragonetti, N.C. and Edvinsson, L. (1997). Intellectual capital: navigating the new business landscape. London: Macmillan Press Ltd.

Sackett, P.R. and Roth, L. (1996). Multi-stage selection strategies: a Monte Carlo investigation of effects on performance and minority hiring. Personnel Psychology, 49, 549-572.

Taylor, H.C. and Russell, J.T. (1939). The relationship of validity coefficients to the practical effectiveness of tests in selection: discussion and tables. Journal of Applied Psychology, 23, 565-578.

van der Linden, W.J. (1981). Using aptitude measurements for the optimal assignment of subjects to treatments with and without mastery scores. Psychometrika, 46, 257-274.

van der Linden, W.J. (1987). The use of test scores for classification decisions with threshold utility. Journal of Educational Statistics, 12, 62-75.

van der Linden, W.J. and Vos, H.J. (1996). A compensatory approach to optimal selection with mastery scores. Psychometrika, 61, 155-172.

Vos, H.J. (1997a). Simultaneous optimization of quota-restricted selection decisions with mastery scores. British Journal of Mathematical and Statistical Psychology, 50, 105-125.

Vos, H.J. (1997b). A simultaneous approach to optimizing assignments with mastery scores. Multivariate Behavioral Research, 32, 403-433.

Vos, H.J. (2001). A minimax procedure in the context of sequential testing problems in psychodiagnostics. British Journal of Mathematical and Statistical Psychology, 54, 139-159.

Wolfram, S. (1996). The Mathematica book (3rd ed.). Cambridge: Cambridge University Press.