Psicothema was founded in Asturias (northern Spain) in 1989, and is published jointly by the Psychology Faculty of the University of Oviedo and the Psychological Association of the Principality of Asturias (Colegio Oficial de Psicología del Principado de Asturias).
We currently publish four issues per year, which accounts for some 100 articles annually. We admit work from both the basic and applied research fields, and from all areas of Psychology, all manuscripts being anonymously reviewed prior to publication.
Psicothema, 2000. Vol. Vol. 12 (nº 3). 487-494
Juan C. Oliver, Jesús Rosel y Pilar Jara
Universitat Jaume I
Es frecuente en la investigación comportamental que el proceso de recogida de datos no siga los principios del muestreo aleatorio simple supuesto por la regresión clásica, sino un muestreo por agrupamientos (cluster sampling) en donde junto con los participantes se selecciona también unidades contextuales a las que éstos pertenecen tales como escuelas, municipios o empresas. La consecuencia de utilizar regresión ordinaria es la producción de sesgos en el error típico de medida y un aumento en la probabilidad de cometer errores de inferencia. El análisis multinivel modela explícitamente estas relaciones jerárquicas proporcionando además estimaciones sobre la variabilidad contextual de los coeficientes de regresión. El objetivo del trabajo es simplificar el análisis multinivel como una generalización del análisis de covarianza, a partir de conceptos estadísticos más comunes como los diseños de medidas repetidas, modelos de efectos fijos y aleatorios. Se presentan ejemplos de aplicaciones en el contexto de la psicología escolar.
Multilevel regression models: Applications in school psychology. Data collection procedures in the behavioral sciences do not always follow the rules of simple random sampling, an assumption of ordinary least squares regression. This is the case in cluster sampling designs which contain more than one type of experimental unit, such as subjects that are nested within classes, schools or companies. Failure of taking into consideration the special structure of the data results in estimation bias for the standard error and in an increase in the probability of inference errors. Multilevel analysis models this relationship among the observations while providing unbiased standard error and estimates of the contextual variability of regression coefficients. The purpose of this paper is to simplify multilevel analysis as a generalization of the analysis of covariance on the basis of commonly used statistical concepts such as repeated measures designs, fixed and random effects models. Several application examples in school psychology are reviewed.
La distinción entre modelos estadísticos de efectos fijos, aleatorios y mixtos fue planteada por Eisenhart (1947) y se ha convertido en nomenclatura básica en la estadística aplicada de nuestros días. En un diseño de investigación, un factor es aleatorio si sus niveles consisten en una selección al azar de una población de niveles posibles. Un factor es considerado fijo, si sus niveles son escogidos premeditadamente y por un procedimiento no aleatorio (Milliken y Johnson, 1992). Por ejemplo, en una muestra al azar de profesores en un estudio experimental sobre la influencia de distintos estilos de enseñanza en el rendimiento, la variable profesor constituiría un factor aleatorio. Si comparamos en cambio la eficacia de tres métodos didácticos concretos (A, B y C por ejemplo), éstos constituirían un factor de efectos fijos ya que se está específicamente interesado en estos métodos y no en otros. Se considera un modelo de efectos mixtos a aquél en el que uno o más factores son fijos y al menos uno es aleatorio. Una combinación de los dos estudios arriba citados sería un ejemplo de diseño mixto que permitiría evaluar de forma conjunta tanto los métodos de enseñanza (A, B, C), como la variabilidad en el efecto de los profesores y la interacción entre ambos factores sobre el rendimiento. Conviene aclarar que la literatura psicológica (Myers y Well, 1991; Keppel y Zedeck, 1989) se refiere a veces a un diseño mixto como una combinación de factores intra y entre sujetos. La acepción de efectos mixtos que se da en la literatura multinivel es un poco más general. El sujeto en un modelo de medidas repetidas es típicamente un factor aleatorio; sin embargo no es necesaria la existencia de un factor intrasujetos para combinar los dos tipos de efectos, tal como se ve en el ejemplo anterior. La clarificación de Eisenhart (1947) fue más lingüística que conceptual, en el sentido de que sus términos describían modelos que estaban siendo ya puestos en práctica con anterioridad en el diseño y análisis de experimentos (Tippett, 1931, 1937; Daniels, 1939; Jackson, 1939; Cochran, 1939; Winsor y Clarke, 1940; Ganguli, 1941; Crump, 1946, 1947; Searle, Casella y McCulloch, 1992). Estos modelos han extendido y generalizado el análisis de varianza introducido por Fisher (1918, 1925), surgiendo en contextos de aplicación diversos, como por ejemplo en biología, ingeniería y ciencias del comportamiento.
La utilización de modelos con efectos aleatorios ha sido un poco más tardía en el análisis de regresión, aunque existen antecedentes tempranos (Cochran, 1946; Tukey, 1951; Anderson y Bancroft, 1952). El análisis multinivel es básicamente un modelo de regresión de efectos mixtos, en donde se intenta estudiar una relación lineal entre dos variables en estudios donde se ha realizado muestreo por agrupamientos (cluster sampling) (Goldstein, 1986a). Esto ocurre cuando en una investigación psicológica existen, además de los sujetos, otras unidades de análisis tales como escuelas, municipios, empresas, hospitales, etc. La existencia de estas agrupaciones naturales queda reflejada en la estructura de los datos; esto hace que se incumpla el supuesto del muestreo aleatorio simple y que muchas técnicas estadísticas convencionales, tales como el Análisis de Varianza (ANOVA) de efectos fijos o la regresión clásica sean inapropiadas. Esto es debido a que se producen sesgos en la estimación del error típico de medida y un aumento en la probabilidad de cometer el error de rechazar la hipótesis nula cuando ésta es cierta. El análisis multinivel modela explícitamente estas relaciones jerárquicas, eliminando estos sesgos, proporcionando además estimaciones de interés psicológico sobre la variabilidad y replicabilidad de los coeficientes de regresión en los distintos contextos sociales (Robinson, 1950), y sobre la influencia de éstos en el comportamiento del individuo.
Un investigador educativo puede, por ejemplo, ir a un grupo de escuelas y recoger datos sobre el nivel socioeconómico de los alumnos y su rendimiento académico, a fin de constatar si existe una relación funcional entre ambas variables. Tendríamos así dos tipos de unidades experimentales: el sujeto y la escuela, correspondientes a lo que en la literatura se denomina también como primer y segundo nivel de análisis (Goldstein, 1986a). En el caso del sujeto, la variable de interés es el rendimiento académico. En el caso de las escuelas, las variables de interés son sus respectivas medias y pendientes de asociación entre nivel socioeconómico y rendimiento, expresadas mediante los estimadores de sus rectas de regresión. El objetivo del análisis multinivel consiste en constatar si existe variabilidad en las rectas de regresión entre las distintas escuelas. De esa manera, y mediante una consideración integrada de ambos niveles de análisis, se pretende cuantificar y contrastar hipótesis estadísticas acerca de la incidencia de los distintos contextos académicos en el rendimiento escolar y en su relación con el nivel socioeconómico del niño. Existe en la literatura una proliferación algo redundante y en ocasiones confusa para el investigador usuario de estos métodos. El objetivo del trabajo es simplificar y presentar el análisis multinivel como una generalización del análisis de covarianza, y a partir de conceptos estadísticos más comunes tales como los diseños de medidas repetidas y la distinción entre modelos de efectos fijos y aleatorios.
Análisis Multinivel y Análisis de Covarianza
La relación entre un modelo multinivel y el análisis de covarianza es análoga a la diferencia entre una prueba t de Student para grupos independientes, y otra prueba t para medidas repetidas. La diferencia radica en la matriz de varianzas-covarianzas de la distribución de observaciones. Imaginemos un experimento sobre la eficacia de un determinado refuerzo conductual sobre la colaboración de niños en tareas domésticas. En el primer caso, podríamos formular la distribución de las observaciones según el modelo lineal de la siguiente manera:
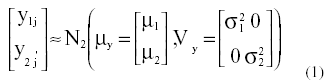
en donde j y j’ son sujetos distintos asignados a dos condiciones de refuerzo (1 y 2). Este es un modelo típico de efectos fijos, puesto que sólo hay un único componente de varianza, σ2 (si asumimos, igualmente, que σ21 = σ22), correspondiente a las diferencias individuales en cada grupo de refuerzo.
En un modelo de medidas repetidas, en cambio, la distribución sería la siguiente:

para j = 1,2,3,...,n niños
en donde y1j e y2j son resultados del mismo niño en las condiciones antes y después del refuerzo; µ1 y µ2 son las medias poblacionales en cada caso, o efectos fijos. Se asume que σ21 = σ2 2, que llamaremos abreviadamente σ2. La diferencia básica entre ambos modelos está en que existe asociación entre las observaciones. Mientras que en el primer caso las mediciones realizadas en los niños son independientes, en el segundo caso la matriz de varianzas covarianzas contiene un elemento adicional (σ12). Es precisamente esta característica la que hace necesario el uso de distintas estrategias de análisis específicas, y por la que se considera que el modelo de medidas repetidas es un modelo de componentes de varianza o de efectos aleatorios.
Una situación análoga en un contexto de regresión diferencia el análisis de covarianza clásico del modelo multinivel. Recordemos que el primero es una combinación de un análisis de varianza y de regresión clásico. Se haría un análisis de regresión ordinario, por ejemplo, entre el número de horas de preparación para un examen y rendimiento académico a fin de estudiar la eficacia de los hábitos de estudio en una población de niños. En el análisis de covarianza clásico se incluiría el estudio de esta relación en un diseño de dos o más grupos, como por ejemplo, dos tipos de entrenamiento en hábitos de estudio con respecto a un grupo de control. Los sujetos en este caso podrían ser asignados aleatoriamente a uno de los grupos, y se podrían contrastar hipótesis tanto sobre las diferencias entre los métodos de estudio, como sobre la eficacia del tiempo invertido. Los efectos de interés en este caso son fijos, puesto que se han elegido premeditadamente dos programas de entrenamiento de estudio específicos frente a un grupo de control. Tendríamos un análisis de covarianza de efectos mixtos o modelo multinivel si en lugar de estos programas concretos, el objetivo del estudio fuera, por ejemplo, el contrastar la eficacia de las horas de estudio en una selección de escuelas al azar. En este caso habría dos tipos de unidades experimentales, la escuela y el niño, y las medidas de los niños dentro de cada escuela estarían correlacionadas, por lo que el modelo de efectos fijos no sería apropiado. Como consecuencia, la matriz de covarianzas del modelo multinivel contará con más de un componente.
Modelo con pendiente común entre grupos
Bajo el supuesto de igualdad de pendientes entre escuelas (ver
Figura 1a), el componente de varianza adicional (σ20)
representa la covarianza entre las observaciones intraescuelas realizadas en
los niños (ver Tabla 1). Es práctica común en estos casos
el centrar los valores de la variable predictora (Xi -
![]() ); es decir, el expresarlos
como desviaciones respecto de su media, en lugar de mantener la métrica
original. La ventaja de este procedimiento es que el punto de corte en origen
de cada recta de regresión para cada grupo se convierte en la media aritmética de su variable dependiente (ver Figura 2). Esto facilita la interpretación
de los resultados y la realización de inferencias sobre los parámetros,
ya que a menudo las variables psicológicas son medidas en escalas de
intervalo y el origen es difícilmente interpretable. Tras este procedimiento
de centrado en el ejemplo anterior, σ20 representa también la varianza de las medias entre escuelas.
); es decir, el expresarlos
como desviaciones respecto de su media, en lugar de mantener la métrica
original. La ventaja de este procedimiento es que el punto de corte en origen
de cada recta de regresión para cada grupo se convierte en la media aritmética de su variable dependiente (ver Figura 2). Esto facilita la interpretación
de los resultados y la realización de inferencias sobre los parámetros,
ya que a menudo las variables psicológicas son medidas en escalas de
intervalo y el origen es difícilmente interpretable. Tras este procedimiento
de centrado en el ejemplo anterior, σ20 representa también la varianza de las medias entre escuelas.
Modelo con pendiente cambiante entre grupos
El supuesto de pendientes iguales para los distintos grupos puede no estar justificado, por lo que conviene contrastar estadísticamente su homogeneidad. En el ejemplo anterior, pudiera existir variabilidad entre escuelas en el rendimiento adicional obtenido por cada hora de estudio invertida por sus alumnos. En este caso, la covarianza intragrupos incluye dos parámetros adicionales: la varianza de las pendientes de las distintas escuelas (σ21) y la covarianza entre la media y las pendientes de las escuelas (σ01). Las Figuras 1a, 1b y 1c ilustran gráficamente el significado de estos parámetros. Bryk y Raudenbush (1992) presentan un ejemplo con variabilidad significativa de las pendientes entre nivel socioeconómico y rendimiento para diferentes escuelas, en donde algunas de éstas magnifican las desigualdades iniciales y otras las compensan. El modelo multinivel ha sido así instrumental para describir la naturaleza de las diferencias entre los efectos del proceso educativo en distintos centros escolares.
Elaboración y Generalización del Modelo con Coeficientes Aleatorios
A fin de explicar o dar cuenta de la variabilidad observada, se pueden construir modelos más complejos. Para ello, incluiríamos nuevas unidades experimentales o niveles, y / o nuevos factores de efectos fijos o aleatorios, que pueden ser tanto variables de clasificación como covariantes en cada nivel de análisis. Veamos algunos ejemplos relacionados con el caso anterior.
Inclusión de nuevas variables de clasificación
Pongamos por caso que se quiere incluir la variable Tipo de Escuela en el ejemplo anterior. Este sería un factor de clasificación para las unidades de nivel 2, y de efectos fijos si se está interesado de antemano en los niveles de escuela pública y privada. Más formalmente, se tendría el siguiente modelo lineal, para el que los efectos fijos aparecen en letras griegas y los efectos aleatorios en letras latinas:
![]()
para h = 1 y 2 tipos de escuela (pública y privada)
i = 1, 2,..., ah escuelas dentro de cada tipo,
j = 1, 2, 3,..., ni sujetos por escuela
En este caso se podrían contrastar las siguientes hipótesis adicionales en el intento de explicar o dar cuenta de variabilidad significativa en los coeficientes de regresión en el apartado anterior.
![]()
Ambas especifican posibles efectos del tipo de escuela pública o privada (primer subíndice) sobre el rendimiento académico. Si ninguna de estas diferencias fuera significativa, se podría reducir el modelo al expuesto en la fórmula (7). Si en cambio rechazáramos alguna o ambas de estas hipótesis nulas, se habría explicado parte de las diferencias observadas entre escuelas en el modelo (7). El nuevo subíndice h de los efectos aleatorios indica que las estimaciones de los componentes de varianza y covarianza residuales para las escuelas se calcula a partir de las desviaciones con respecto a la media del tipo de centro al que pertenece (sea público o privado), y no con respecto a la media total. Es decir, se trata de varianzas y covarianzas condicionales, que cuantifican diferencias entre escuelas de las que los efectos fijos del modelo no dan cuenta.
Inclusión de nuevas covariantes
La capacidad de predicción de un modelo puede mejorar a veces con la incorporación de covariantes medidas en cualquiera de sus unidades experimentales o niveles. La tradición de una escuela medida en años de existencia para cada una de ellas, o una medida de ajuste o adaptación social para cada alumno como predictor de rendimiento académico serían ejemplos de covariantes de nivel dos y uno, respectivamente. Con este último ejemplo de covariante en nivel uno, y a partir de la expresión (7) en la Tabla 2 podríamos elaborar el siguiente modelo:
![]()
para i = 1, 2, ..., a escuelas
y j = 1, 2, ..., ni sujetos por escuela.
Sería posible el contrastar aquí tres nuevas hipótesis estadísticas:
![]()
H07 hace referencia al efecto fijo de asociación lineal entre ajuste social y rendimiento académico. H08 intenta constatar si esta relación lineal cambia de escuela a escuela, mientras que H09 informará sobre el patrón concreto de variación de esta asociación lineal entre adaptación social y rendimiento académico en los distintos centros educativos (ver Figuras 1b, 1c y 1d, como referencia).
Inclusión de nuevos niveles de análisis
Otra posible concreción del modelo original consistiría en incorporar una unidad experimental de tamaño intermedio, como la clase. De este modo, los sujetos (Nivel 1) estarían agrupados en clases (Nivel 2), y éstas en escuelas (Nivel 3). Puede que la influencia de las escuelas se deba más que a la institución en sí misma, a ciertas características propias de sus clases: métodos de enseñanza, tamaño, cualificación de los profesores, etc.. Este modelo dará pie a realizar un análisis más fino en este sentido. Se asume que todas estas unidades experimentales han sido escogidas de forma aleatoria a partir de poblaciones de sujetos, clases y escuelas definidas de antemano. Más formalmente:
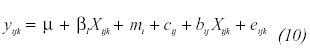
para i = 1, 2,..., a escuelas
j = 1, 2,..., b clases por escuela y
k = 1, 2,..., n sujetos por clase
Aquí se podrían contrastar las siguientes hipótesis de interés frecuente, y adicionales a las que figuran en el modelo (7) de la Tabla 2:
![]()
Las hipótesis a contrastar hacen referencia a las varianzas y covarianza entre los coeficientes de regresión entre clases una vez han sido estimados los efectos de las escuelas en donde éstas se encuentran agrupadas. El sufijo c indica que las estimaciones de los coeficientes residuales se han hecho en este caso para cada una de las clases muestreadas. De esta manera, se podrá evaluar el efecto de pertenencia a diferentes clases sobre el rendimiento académico medio, y sobre la pendiente de asociación entre éste y el nivel socioeconómico. Si alguno de estos coeficientes resultara significativo, se podría dar cuenta de esta variabilidad observada incorporando covariantes en el modelo o variables de clasificación de los tipos de clases pertinentes en el estudio.
Estos ejemplos puntuales de elaboración del modelo de la Tabla 2 pueden combinarse en un modelo único. Asimismo, es posible añadir variables de clasificación y covariantes en más de un nivel de análisis. Pongamos por caso que se incluye el sexo del sujeto como variable de clasificación en el nivel 1, y el tamaño de la clase como covariante en el nivel 2. Ambos efectos serían fijos en su nivel de análisis propio, y aleatorios en su interacción con las unidades de análisis superiores, sea la clase, la escuela o ambas. Por ejemplo, puede que se encuentre diferencias generales entre niños y niñas en una clase de lenguaje (efectos fijos), pero que estas diferencias se magnifiquen o reduzcan según la clase o la escuela (efectos aleatorios). Bryk y Raudenbush (1992), Goldstein (1995) y Longford (1993) contienen exposiciones más exhaustivas y detalladas del modelo general con un número indeterminado de niveles, a donde se remite al lector interesado. A continuación se revisarán algunos conceptos de inferencia en el análisis multinivel que son de utilidad, tanto para la adecuada comprensión del modelo, como para la realización de análisis y la interpretación de resultados.
Aspectos de Inferencia Estadística
Estimación
Componentes de varianza. La existencia de covarianza entre observaciones hace que el modelo de regresión por mínimos cuadrados ordinarios produzca sesgos en la estimación del error típico, y producirá como consecuencia errores de inferencia. En una situación similar al ejemplo anterior, el grado de sesgo depende de la magnitud de la covarianza intra grupos tanto de la variable dependiente como de la predictora, así como del número de unidades experimentales de primer y segundo nivel. Goldstein (1995) ha calculado que en circunstancias usuales de muestreo el valor calculado del error típico estimado mediante una regresión ordinaria puede ser la mitad del valor real, produciendo así intervalos de confianza excesivamente estrechos y un aumento de la probabilidad de Error Tipo I en los contrastes de hipótesis. Para evitarlo hay que recurrir a procedimientos que nos permitan estimar todos los parámetros del modelo.
Soluciones analíticas para la estimación de componentes de covarianza pueden encontrarse solamente en algunos casos en donde haya equilibrio entre el número de observaciones por condición, tal como ocurre análogamente en el caso de los diseños experimentales balanceados. En un contexto de regresión esto implica que no solamente el número de unidades de Nivel 1 sea el mismo para cada unidad experimental de Nivel 2, sino también que la distribución de los valores de la variable predictora (Xs) sea también la misma para todos los grupos de nivel superior (Bryk y Raudenbush, 1992). En la práctica de estudios de campo en psicología, es frecuente que esta situación no se cumpla. Tal como ocurre en el análisis de experimentos en estos casos, es aconsejable aquí también el recurrir a procedimientos de Máxima Verosimilitud (MV) iterativos, ya que producen estimadores con propiedades deseables con muestras grandes, tales como consistencia y eficiencia: es decir, si se recoge gran cantidad de datos, el estimador será aproximadamente insesgado y con varianza mínima (Bryk y Raudenbush, 1992). El desarrollo y clarificación de los métodos anteriores fue hecho por Hartley y Rao (1967), quienes propusieron una serie de ecuaciones de MV muy generales aplicables a modelos de efectos mixtos y aleatorios, con o sin covariantes y datos equilibrados o desequilibrados. Sobre la base de estas ideas se ha desarrollado en los años ochenta y noventa algoritmos para la estimación de componentes de varianza, incluidos en programas tales como MLWin en la universidad de Londres (Goldstein, 1986b; Goldstein et. al., 1998) o el módulo Proc Mixed del Sistema SAS (Littell, Milliken, Stroup y Wolfinger, 1996).
Coeficientes de regresión fijos. Los procedimientos de MV aplicados a la estimación de coeficientes de regresión fijos de tendencia central (µ, ß1) generan expresiones contenidas en las ecuaciones del modelo mixto (Hocking, 1995; Henderson, 1984; Diggle, Liang y Zeger, 1994). Estas son equivalentes a las ecuaciones de mínimos cuadrados generalizados, que representan una extensión natural de las ecuaciones normales o de mínimos cuadrados ordinarios en la regresión clásica para aquellos casos en que el modelo contenga estructuras de covarianza más complejas. Las estimaciones de los coeficientes de regresión de efectos fijos mediante el procedimiento de mínimos cuadrados generalizados necesita de los resultados de la fase anterior de estimación de componentes de varianza, teniendo propiedades tales como la de ser mejores estimadores lineales insesgados (Littell, Milliken, Stroup y Wolfinger, 1996).
Coeficientes de regresión aleatorios. Además de los coeficientes fijos de regresión de tendencia central, las desviaciones aleatorias en la media o pendiente propias de cada unidad jerárquica de nivel superior pueden ser de interés substantivo. En el ejemplo anterior, los efectos fijos indican las tendencias centrales de asociación lineal entre nivel socioeconómico y rendimiento académico, mientras que los aleatorios indican las desviaciones en medias y pendientes de las escuelas particulares. La solución de las ecuaciones del modelo mixto generadas por el procedimiento de máxima verosimilitud nos proporciona también estos estimadores o predictores, que son función tanto de los coeficientes de regresión fijos como de los componentes de varianza. En el ejemplo anterior, el método pondera la magnitud de los coeficientes en función de la cantidad de información que se posee para cada escuela y de la varianza entre escuelas. Una muestra escasa para una escuela concreta así como varianzas pequeñas entre escuelas provocarán que el algoritmo acerque el coeficiente aleatorio predicho para una escuela concreta a los coeficientes fijos de tendencia central. Aunque el uso de estos estimadores encogidos ha causado debates en la comunidad estadística, se ha podido ver que resultan en un error de predicción menor de los resultados obtenidos con muestras nuevas (Effron y Morris, 1975; Bryk y Raudenbush, 1992). Se ha mostrado como en general éstos tienen la propiedad de ser mejores predictores lineales insesgados (Harville, 1976).
Contrastes de hipótesis
Además de estimar los componentes de varianza para un modelo concreto, el investigador quiere por lo común realizar contrastes de hipótesis sobre los mismos. Para ello, un procedimiento general utilizado en los programas anteriores es el de razón de verosimilitud (likelihood ratio test ), que permite contrastar una Ho frente a una Ha que contiene un mayor número de parámetros. El estadístico utilizado es el siguiente:
![]()
en donde λ0 y λ1 representan los valores de verosimilitud (likelihoods ) de los modelos correspondientes a la hipótesis nula y a la hipótesis alternativa. El valor D obtenido es contrastado en una Tabla χ2 con grados de libertad igual a la diferencia en el número de parámetros de ambos modelos (Goldstein, 1995; Raudenbush y Bryk, 1992). Imaginemos que en el ejemplo (5) de la Tabla 1 queremos contrastar la hipótesis nula de que no hay variabilidad en el rendimiento académico medio entre escuelas:
![]()
Estos dos modelos difieren en la incorporación de un parámetro adicional bajo la hipótesis alternativa. Por este motivo, tras la estimación de sus respectivas verosimilitudes, el valor D será contrastado con el de una distribución χ2 con 1 grado de libertad. El nivel de significatividad estadística proporcionará la evidencia para concluir si hay o no variabilidad en el rendimiento académico medio entre escuelas. La aceptación de la hipótesis nula indicaría que no hace falta un modelo multinivel para evaluar H01 : β1 = 0; un análisis de regresión por mínimos cuadrados ordinario sería suficiente (Modelo (3) de la Tabla 1). El procedimiento de razón de verosimilitud puede ser también utilizado de forma análoga para contrastes de hipótesis sobre los efectos fijos del modelo.
Otra ventaja de estos métodos de inferencia es su flexibilidad para realizar contrastes sobre combinaciones lineales de las varianzas del modelo. En el ejemplo anterior, es posible determinar si las varianzas de los niños (Nivel 1) cambian con el status socioeconómico, si hay diferencias en la variabilidad de niños y niñas, o si estas diferencias dependen de la edad o de si la escuela es pública o privada. En estos casos, los componentes de covarianza tienen una interpretación análoga a los efectos de interacción en efectos fijos. La descripción de estas diferencias en los componentes de varianza nos es útil para mejorar la especificación del modelo a ajustar, aunque también pueden ser de interés psicológico (Godstein et al., 1998; Goldstein, 1995).
Aplicaciones
Buena parte de las primeras aportaciones del análisis de regresión multinivel han sido realizadas en el ámbito de la psicología escolar. Aitkin y Longford (1986) hacen una revisión exhaustiva de los métodos utilizados hasta entonces en estudios clásicos de comparación de la eficacia de diferentes escuelas sobre el rendimiento académico. Típicamente, en estos estudios originales con regresión clásica no existía un reconocimiento de la estructura jerárquica de los datos, no habiendo además una distinción entre componentes de regresión intra y entre escuelas. Era frecuente por ejemplo aplicar una regresión ordinaria al conjunto de medias del rendimiento y de la variable predictora de las escuelas. Además de los sesgos a que puede dar lugar este procedimiento (Woodhouse y Goldstein, 1988), el análisis es ineficiente en cuanto que no se está incluyendo las medidas individuales de cada niño (Paterson y Goldstein, 1991; Woodhouse y Goldstein, 1988). Utilizando esta información, Aitkin y Longford (1986) encontraron algunas escuelas con pendientes desiguales de asociación entre razonamiento verbal previo al ingreso en la escuela y rendimiento académico posterior, por lo que algunas escuelas parecen magnificar las diferencias iniciales entre niños mientras que otras parecen compensarlas. Estudios similares han mostrado como la desventaja de minorías étnicas en el rendimiento en matemáticas parece magnificarse en escuelas norteamericanas públicas en comparación con las privadas (Lee y Bryk, 1989; Nuttall, Goldstein, Prosser y Rashbash, 1988). Estos resultados proporcionan una descripción ajustada de los procesos educativos de la que no se disponía antes del uso de estas metodologías.
Un frente más general de aplicaciones surge en la psicología del desarrollo y del aprendizaje. En los análisis clásicos intrasujetos, bien univariados o multivariados, las diferencias individuales en el crecimiento son relegadas a la interacción de las medidas repetidas por sujetos. El análisis multinivel, en cambio, proporciona un modelo explícito de la variabilidad en el cambio personal, considerando al sujeto como nivel 2, y a las medidas repetidas como observaciones anidadas de Nivel 1 (Bryk y Raudenbush, 1992). Las estimaciones de los coeficientes aleatorios personales proporciona una ecuación de crecimiento para cada sujeto. La inclusión de efectos fijos (sexo, alimentación, número de hermanos) o nuevos niveles de análisis (escuela, comarca, provincia...) permitirá estudiar sus efectos sobre las curvas de crecimiento. En un estudio sobre el aprendizaje de las ciencias naturales, Lord (1980) encontró componentes de varianza significativos de variabilidad entre sujetos tanto en status inicial, como en el cambio en función de la edad. La incorporación del lenguaje materno y número de horas de instrucción reveló efectos sobre estas diferencias de desarrollo. Huttenlocher, Haight, Bryk y Seltzer (1991) encontraron diferencias individuales no sólo en la asociación lineal de la edad con el incremento del vocabulario en niños entre 14 y 26 meses, sino también en los coeficientes de regresión cuadráticos. Tanto el sexo como el nivel de uso del lenguaje por la madre en casa eran buenos predictores de los diferentes patrones de aceleración y desaceleración observados en los niños en el aprendizaje de nuevas palabras. Modelos similares a los anteriores se han aplicado también a la psicología organizacional y del trabajo en sentido más amplio (Bryk y Raudenbush, 1992).
Buena parte de las técnicas estadísticas clásicas de uso común en psicología y basadas en el muestreo aleatorio simple tienen o pueden tener una versión multinivel para muestreos por agrupamientos (cluster sampling ). Goldstein (1995) y Longford (1993) extienden el análisis multinivel a medidas repetidas, a casos de variables discretas con distribuciones no normales, o a modelos multivariados como el análisis factorial. En este sentido, podemos decir que se trata de una técnica de amplio espectro, muchos de cuyos desarrollos y aplicaciones potenciales en psicología están todavía en gestación.
Agradecimientos
Este trabajo ha sido parcialmente financiado por la Fundación Bancaja-Castellón (Proyecto P1B95-20).
Aitkin, M. y Longford,N. (1986). Statistical modelling in school effectiveness. Journal of the Royal Statistical Society A, 149, 1-43.
Anderson, R. L. y Bancroft, T. A. (1952). Statistical theory in research. New York: McGraw-Hill.
Bryk, A. S. y Raudenbush, S. W. (1992). Hierarchical linear models: Applications and data analysis methods. Newbury Park, CA: Sage Publications.
Cochran, W. G. (1939). The use of the analysis of variance in enumeration by sampling. Journal of the American Statistical Association, 34, 492-510.
Cochran, W. G. (1946). Analysis of covariance. A paper presented at the Institute of Mathematica Statistics, Princeton University.
Crump, S. L. (1946). The estimation of variance components in the analysis of variance. Biometrics, 2, 7-11
Crump, S. L. (1947). The estimation of variance in multiple classification. Ph.D. Thesis. Iowa State University, Ames Iowa.
Daniels, H. E. (1939). The estimation of components of variance. Journal of the Royal Statistical Society Suppl., 6: 186-197.
Diggle, P. J., Liang, K. y Zeger, S. L. (1996). Analysis of longitudinal data. Oxford UK: Clarendon Press.
Eisenhart, C. (1947). The assumptions underlying the analysis of variance. Biometrics, 3: 1-21.
Effron, B. y Morris, C. (1977, Mayo). Stein´s paradox in statistics. Scientific American, pp. 119-127.
Fisher, R. A. (1918). The correlation beween relatives on the supposition of mendelian inheritance. Transactions of the Royal Society of Edinburgh, 52, 399-433.
Fisher, R. A. (1925). Statistical methods for research workers. Edinburgo y Londres: Oliver y Boyd,.
Ganguli, M. (1941). A note on nested sampling. Sankhya, 5, 449-452.
Goldstein, H. (1986a). Multilevel statistical models. London, Arnold.
Goldstein, H. (1986b) Multilevel mixed linear model analysis using iterative generalized least squares. Biometrika, 73 (1), pp. 43-56.
Goldstein, H. (1995). Multilevel Statistical Models (2nd. Ed.). London: Arnold.
Golsdstein, H., Gashbash, J., Plewis, I., Draper,D., Browne, W., Yang, M., Woodhouse, G y Healy, M. (1998). A user´s guide to MLWin. London: University of London, Institute of Education.
Hartley, H. O. y Rao, J. N. K. (1967). Maximum likelihood estimation for the mixed analysis of variance model. Biometrika, 54, 93-108.
Harville, D. A. (1976). Extension of the Gauss-Markov theorem to include the estimation of random effects. Annals of Statistics, 2, 384-395.
Henderson, C. R. (1984). Applications of linear models in animal breeding. Guelf, Canada: University of Guelf.
Hocking, R. R. (1996). Methods and applications of linear models. New York: Wiley.
Huttenlocher, J. E., Haight, W., Bryk, A. S. y Seltzer, M. (1991). Early vocabulary growth: Relation to language input and gender. Developmental Psychology, 27 (2), 236-249.
Jackson, R. W. B. (1939). Reliability of mental tests. British Journal of Psychology, 29, 267-287.
Keppel, G. y Zedeck, S. (1989). Data analysis for research designs. San Francisco: Freeman.
Latour, S. A., y Miniard P. W. (1983). The Misuse of repeated measures analysis in marketing research. Journal of Marketing Research, Vol XX, 45-57.
Littell, R.C., Milliken, G.A., Stroup, W.W. y Wolfinger, R.D. (1996). SAS System for Mixed Models. Cary NC: SAS Institute.
Longford, N. T. (1993) Random coefficient models. Oxford UK: Oxford University Press.
Lee, V. y Bryk, A. S. (1989). A multilevel model of the social distribution of achievement. Sociology of Education, 62, 172-192.
Lord, F. M. (1980). Aplications of item response theory to practical testing problems. Hillsdale NJ: Erlbaum.
Milliken, G. A. y Johnson, D. E. (1992). Analysis of messy data (Vol. 1): Designed experiments. New York: Chapman y Hall.
Myers, J. L. y Well A. D. (1991). Research Design and Statistical Analysis. New York: Harper Collins Publishers.
Nuttall, D., Goldstein, H., Prosser, R., y Rashbash, J. (1988). Differential school effectiveness. International Journal of Educational Research, 13, 769-76.
Paterson, L. y Goldstein, H. (1991). New statistical methods for analysing social structures: an introduction to multilevel models. British Educational Research Journal, 17 (4), 387-393.
Robinson, W. S. (1950). Ecological correlations and the behavior of individuals. American Sociological Review, 15, 351-57.
Satterthwaite, F. E. (1946). An approximate distribution of estimates of variance components. Biometrics Bulletin, 2: 110-14.
Searle, S. R., Casella, G. y McCulloch, C. E. (1992) Variance components. New York: John Wiley y Sons.
Tippett, L. H. C. (1931, 1937). The Methods of Statistics. London: William and Norgate Ltd.
Tukey, J. (1951). Components in regression. Biometrics, 7, 33-69.
Winsor, C. P. y Clarke, G. L. (1940). A statistical sudy of variation in the catch of plankton nets. Sears Foundation Journal of Marine Research, 3, 1-27.
Woodhouse, G. y Goldstein, H. (1988). Educational performance indicators and LEA League Tables. Oxford Review of Education, 14 (3), 301-320.
Aceptado el 20 de octubre de 1999