Psicothema, 2000. Vol. Vol. 12 (Suplem.2). 288-291

Ana Hernández Baeza, José Muñiz^* y Eduardo García Cueto^*

Universidad de Valencia y ^* Universidad de Oviedo

En el presente estudio se evalúa el modo en que la variación del número de categorías de respuesta en escalas ordinales afecta al comportamiento del modelo de respuesta graduada en la versión propuesta por Muraki (1990). Dicho comportamiento es evaluado mediante el programa Parscale 3.2 (Muraki y Bock, 1998) a partir de un conjunto de datos simulados - unidimensionales y bidimensionales - y mediante una muestra empírica. En general los resultados muestran que, cuando los datos son unidimensionales, el mejor ajuste se consigue entre 4 y 6 categorías, estimándose satisfactoriamente el parámetro Θ . Cuando los datos son bidimensionales es necesario un mínimo de 6 categorías para lograr un ajuste satisfactorio, siendo las estimaciones de Θ una estimación del promedio de los dos factores subyacentes.

Effects of the scale number of categories on the Muraki Graded Response Model. Effects that variation in the number of categories in ordinal scales has on the Graded Response Model (as proposed by Muraki (1990)) are evaluated by means of Parscale 3.2 (Muraki and Bock, 1998). Two sets of simulated data (unidimensional and bidimensional) and an empirical data set are analyzed. General results show that when data are unidimensional, the best goodness of fit indices are achieved between 4 and 6 categories. Satisfactory estimates of parameter Θ are also obtained. When data are bidimensional 6 categories are needed as a minimum to achieve satisfactory fit indices. In this case, Θ estimates represent the average between the two latent factors.

Las escalas tipo Likert son unas de las más empleadas en la medición de constructos psicológicos, principalmente en la medida de las actitudes. Al responder a una escala Likert los sujetos han de indicar su grado de acuerdo o desacuerdo con cada uno de los ítems de la escala. Para ello han de posicionarse en una escala de respuesta de ‘acuerdo - desacuerdo’ que cuenta con una serie de categorías politómicas ordenadas, siendo frecuente que el número de categorías varíe en las distintas escalas.

En el marco de la Teoría de la Respuesta a los Items (TRI) se han propuesto distintos modelos unidimensionales para el análisis de este tipo de escalas. Uno de los que más atención ha recibido hasta la fecha es el modelo de Respuesta Graduada de Samejima (1969). Bajo este modelo, la probabilidad de seleccionar una determinada categoría para un cierto ítem, puede calcularse a partir de la función logística:

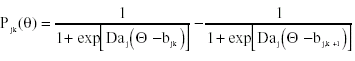
donde a_j es el parámetro de la pendiente para cada ítem, b_{j k} es el parámetro de cada uno de los puntos de corte entre categorías para cada ítem y D es una constante igual a 1.7.

A partir de este modelo, Muraki (1990) propuso una variación considerada más adecuada para las escalas Likert en las que el número de alternativas no varía de ítem a ítem. En esta variación el parámetro b_jk se descompone en dos: b_j que es el parámetro de localización del ítem, y c_k que es el parámetro de localización de cada uno de los puntos de corte entre las categorías, el cual se mantiene constante a través de los distintos ítems. Este modelo permite ordenar los ítems según las estimaciones del parámetro bj, pudiendo estimarse independientemente la distancia psicológica entre las alternativas de la escala.

Puesto que al emplear las escalas Likert se pretende representar adecuadamente un constructo o variable latente de naturaleza continua, la cuestión del número óptimo de alternativas de respuesta y los efectos de la categorización de variables continuas cobra un especial interés. Este tema ha sido tratado en diferentes estudios empíricos y de simulación en relación con temas como la fiabilidad, la estructura factorial y la validez (Bernstein y Eveland, 1982; Comrey y Montag, 1982; Ferrando, 1995; Oswald y Vellicer, 1980; Sancerni, Meliá y González-Romá, 1990; Tomás y Oliver, 1998), no pudiendo ofrecerse un patrón consistente de resultados. Asimismo, también se ha estudiado la pérdida de información que se produce a la hora de representar una variable latente continua a través de distinto número de intervalos (Lehman y Hurlbert, 1972; Jacoby y Matell, 1971; Shaw, Huffman y Haviland, 1987). En estos estudios se recomienda utilizar entre un mínimo de 5 y un máximo de 8 intervalos. Finalmente, desde el marco de la TRI también se ha estudiado el efecto que el número de anclajes ejerce sobre la estimación de los parámetros de los ítems (Gómez, Artes y Deumal, 1989; Bock, 1972) y sobre la función de información (Lord, 1980; Vale y Weiss, 1977). Sin embargo, no se ha estudiado de manera sistemática el modo en que el número de alternativas de las escalas Likert afecta al modelo de Respuesta Graduada, que fue expresamente diseñado para el análisis de este tipo de escalas.

Desde aquí el objetivo del presente trabajo es evaluar de manera sistemática en qué medida el número de categorías de respuesta afecta al comportamiento del modelo de respuesta graduada. Dicho comportamiento es evaluado en términos del ajuste del modelo y de la precisión de las estimaciones del nivel de rasgo Θ. Considerando que a medida que se reduce el número de categorías de las escalas se pierde información relevante para el uso de los modelos de TRI, cabe esperar que la reducción del número de categorías conlleve una disminución del ajuste y de la precisión de las estimaciones. Esta hipótesis es puesta a prueba bajo dos condiciones: cuando se satisface el supuesto de unidimensionalidad que asume el modelo, y cuando se viola dicho supuesto.

Método

Para llevar a cabo el objetivo propuesto se realizó un estudio de simulación, cuyos resultados se compararon con los obtenidos a partir de una muestra empírica. En ambos casos la longitud de la escala fue de 14 ítems y el tamaño muestral fue igual a 1000.

En el estudio de simulación se manipularon dos factores: la dimensionalidad de la escala y el número de categorías de respuesta de la misma. El proceso de generación de los datos constó de dos etapas En la primera etapa se manipuló la dimensionalidad de la escala, considerándose dos condiciones: escala unidimensional y escala bidimensional. En esta etapa los datos fueron generados mediante el programa PRELIS 2 (Jöreskog y Sörbom, 1993). Para la escala unidimensional se partió de un modelo unifactorial, generándose 14 variables continuas con distribución normal. A la hora de fijar el valor de las saturaciones factoriales se tuvieron en cuenta los resultados obtenidos en el análisis factorial exploratorio realizado a partir de la muestra empírica, quedando fijadas las saturaciones a 0.75. Para la escala bidimensional se partió de un modelo bifactorial de factores independientes. De las 14 variables continuas normales generadas, las 7 primeras fueron indicadores del primer factor y las 7 últimas del segundo, quedando las saturaciones factoriales fijadas a 0.75. En una segunda etapa se manipuló el número de categorías de respuesta. En esta etapa, las 14 variables continuas fueron transformadas en variables ordinales discretas. Se realizaron sucesivas reagrupaciones de los datos a través de un programa generado para tal efecto, variándose el número de categorías desde 9 hasta 2. Para cada una de las 16 condiciones de simulación se generaron 70 muestras.

La muestra empírica estuvo formada por 1.000 estudiantes de Psicología de la Universidad de Oviedo. Todos ellos respondieron a un cuestionario de evaluación del profesorado que constaba de 17 ítems, 14 de los cuáles fueron construidos para medir una única dimensión. Se trataba de una escala tipo Likert con 5 alternativas de respuesta. La media muestral fue igual a 3.57 (D.T= 0.93), con un coeficiente de fiabilidad (α) de 0.94. En el análisis factorial realizado se obtuvieron 3 factores. El primero de ellos explicó el 57.8% de la varianza, distando mucho del segundo y tercer factor, por lo que se asumió una estructura esencialmente unidimensional. Al igual que en el estudio de simulación, las 14 variables fueron reagrupadas sucesivamente, reduciéndolas a 4, 3 y 2 categorías de respuesta.

Puesto que todos los ítems presentaban el mismo número de categorías de respuesta, se puso a prueba el modelo de Respuesta Graduada de Samejima en la versión de Muraki (1990) Para ello se empleó el programa Parscale 3.2 (Muraki y Bock, 1998) empleando el método de estimación de máxima verosimilitud. El modelo fue evaluado en términos de la convergencia del proceso iterativo, del ajuste y, en el caso de los datos simulados, de la precisión de las estimaciones del nivel de rasgo.

Resultados

El porcentaje de casos en los que el proceso iterativo convergió a través de las distintas condiciones consideradas se representan en la figura 1. Como puede observarse, el aumento del número de categorías se asocia generalmente a un mayor número de soluciones problemáticas. Esta tendencia se observa tanto para la condición de unidimensionalidad de los datos como para la de bidimensionalidad, si bien en este último caso el problema se acentúa cuando el número de categorías es superior a 6.

El programa PARSCALE, ofrece el estadístico ji-cuadrado como medida de ajuste para cada ítem, proporcionando también la suma de estos valores para evaluar el ajuste del test global. Centrándonos en el ajuste global, en la figura 2 pueden observarse los valores medios de las probabilidades asociadas a χ².

Se constata una clara diferencia en el comportamiento del ajuste del modelo en función de si se cumple o no el supuesto de unidimensionalidad. Concretamente para la condición de datos bidimensionales, al aumentar el número de categorías se produce una mejora progresiva del ajuste del modelo. El número clave de categorías a partir del cuál es posible obtener un buen ajuste se sitúa en 6. Por el contrario, para la condición de datos unidimensionales se observa un buen ajuste del modelo a partir de 4 categorías, siendo éste especialmente bueno cuando el número de categorías oscila entre 4 y 6. A partir de 6 categorías se produce una disminución de los valores de probabilidad asociados a χ², si bien continúan ofreciendo valores que no son estadísticamente significativos

Para evaluar el grado en que las estimaciones del nivel de rasgo (Θ’) diferían de los verdaderos valores de la variable latente generada mediante simulación (Θ), se han calculado los coeficientes determinación de estas variables (r² _{Θ’, Θ}). Asimismo se han considerado los errores estándar asociados a las estimaciones de Θ. Cabe señalar que en el caso de los datos bidimensionales, puesto que el mismo número de variables presentaban saturaciones similares en los dos factores generados, las estimaciones del nivel de rasgo son principalmente un indicador del promedio de los dos rasgos (r²_{Θrasgo1,Θ’}.= 0.411; r²_{Θrasgo2,Θ’}.= 0.407; r²_{Θpromedio,Θ’} = 0.89).

Para la condición de unidimensionalidad, los coeficientes de determinación oscilan entre 0.85 y 0.94 para 2 y 9 categorías respectivamente. Los coeficientes van aumentando ligeramente estabilizándose la magnitud de los mismos entre 4 y 6 categorías (ver figura 3). Para la condición de bidimensionalidad, los coeficientes de determinación (calculados a partir de las estimaciones del parámetro Θ y las puntuaciones promedio en los dos rasgos generados) oscilan entre 0.48 y 0.87. En este caso, la magnitud de los coeficientes aumenta sustancialmente hasta llegar a 5 categorías. A partir de este punto también se estabiliza la magnitud de los coeficientes.

Cabe señalar finalmente que, como era de esperar, la disminución del número de categorías conlleva un aumento de los errores estándar de las estimaciones del parámetro Θ, si bien éstos se estabilizan entre 6 y 7 categorías. Por otra parte, para todas las categorías consideradas, la magnitud de los errores estándar es muy superior para la condición de bidimensionalidad: mientras que para los datos unidimensionales los errores oscilan entre 0.40 y 0.25, para los bidimensionales oscilan entre 0.55 y 0.48.

En los análisis realizados a partir de la muestra empírica, el proceso converge en una solución en todos los casos, independientemente del número de categorías de respuesta empleados. Por otra parte, si bien en todos los casos se rechaza la hipótesis nula de igualdad entre los valores estimados de Θ y las puntuaciones observadas del test, se observa una tendencia a la mejora del ajuste, ya que conforme aumenta el número de categorías, disminuye la ratio entre el valor de χ² y los grados de libertad asociados.

Conclusiones

El objetivo del presente trabajo ha sido evaluar el modo en que el número de categorías de respuesta de las escalas Likert afecta al comportamiento del modelo de respuesta graduada tal y como fue propuesto por Muraki (1990). Puesto que a medida que se reduce el número de categorías de las escalas se pierde información relevante para el uso de los modelos de TRI, parece razonable esperar que a mayor número de categorías de respuesta, mejor sea ajuste del modelo y mayor la precisión de las estimaciones de Θ.

Los resultados obtenidos en el estudio de simulación apoyan la hipótesis anterior sólo parcialmente. En concreto, para las condiciones de unidimensionalidad, resulta indiferente utilizar 2 o 3 categorías, tanto en lo que se refiere al ajuste como a la precisión de las estimaciones. Sin embargo, un nuevo aumento hasta entre 4 y 6 categorías sí mejora el ajuste y la precisión de las estimaciones. Finalmente, a partir de este punto, nuevos aumentos no sólo no producen una mejora sustantiva de la precisión de las estimaciones, sino que, además empeoran el ajuste. Estos resultados, junto con los problemas de convergencia que empiezan a aparecer cuando el número de categorías es superior a 5, hacen que valores en torno a este punto, sean los ideales para lograr el buen funcionamiento del modelo.

Los resultados empíricos son congruentes con los simulados. Si bien la probabilidad asociada a χ² es inferior a 0.001 en todos los casos, se observa que el aumento del número de categorías disminuye la ratio entre el valor de χ² y los grados de libertad. Esta tendencia también se observa en los datos simulados, donde dicha ratio disminuye de 1.81, para 2 categorías a 1.45, 0.96 y 0.93 para 3, 4 y 5 categorías respectivamente.

Los resultados obtenidos, junto con los de otros estudios que se han centrado en la pérdida de información que se produce al categorizar una variable latente continua (Lehman y Hurlbert, 1972; Jacoby y Matell, 1971; Shaw, et al., 1987) ponen de manifiesto que un número muy pequeño de alternativas no resulta adecuado a la hora de representar la variable latente, si bien tampoco se gana información utilizando más de 6 u 8 categorías.

Por otra parte, para las condiciones de bidimensionalidad, no hay diferencias de ajuste entre 2 y 5 categorías, siendo necesario utilizar un mínimo de 6 categorías para aceptar la hipótesis nula de igualdad entre los valores estimados de Θ y los observados a partir del test. Sin embargo, el hecho de que el modelo pueda ofrecer un buen ajuste a los datos bidimensionales no implica que éste resulte adecuado. Si la actitud a medir dependiera de la presencia de dos rasgos igualmente influyentes a la hora de manifestar dicha actitud, de una combinación aditiva de ambos rasgos, la utilización del modelo de respuesta graduada no sería excesivamente grave a pesar de violar el supuesto de unidimensionalidad, siempre y cuando el número de categorías esté como mínimo en torno a 6. Sin embargo, si únicamente uno de los rasgos subyaciera a la actitud que se pretende medir, la violación del supuesto de unidimensionalidad sí tendría consecuencias graves, a pesar de mostrar un buen ajuste. En este caso, las diferencias entre las estimaciones de Θ y los verdaderos valores de cualquiera de los dos rasgos tomados de manera independiente difieren en gran medida.

Bernstein, I H. y Eveland, D. (1982). State vs. trait anxiety: a case study in confirmatory factor analysis. Personality and Individual Differences, 3, 361-372.

Bock, R. D. (1972). Estimating item parameters and latent ability when responses are scored in two or more nominal categories. Psychometrika, 37, 29-51.

Comrey, A. L. y Montag, I. (1982). Comparison of factor analytic results with rwo choice and seven choice personality item formats. Applied Psychological Measurement, 6, 285-289.

Ferrando, P. J (1995). Equivalencia entre los formatos Likert y continuo en items de personalidad: un estudio empírico. Psicológica, 16, 417-428.

Gómez, J; Artés, M. y Deumal, E. (1989). Efecto del número de rangos de la escala de medición sobre la calibración de items y sujetos mediante credit. II Conferencia Española de Biometría, Segovia, Septiembre.

Jöreskog, K. G. y Sörbom, D. (1993). PRELIS 2 user´s reference guide. Chicago: Scientific Software.

Lord, F. M. (1980). Applications of Item Response Theory to practical testing problems. New Jersey, Lawrence Earlbaum Associates.

Muraki, E. (1990). Fitting a polytomous item response model to Likert-type data. Applied Psychological Measurement, 14, 59-71.

Muraki, E y Bock, R. D. (1998). PARSCALE. IRT item analysis and test scoring for rating-scale data. Chicago. Scientific Software International.

Oswald, W. I. y Vellicer, W. F. (1980). Item format and the structure of the Eysenck personality inventory: a replication. Journal of Personality Assessment, 43, 283-288.

Samejima, F. (1969). Estimation of latent ability using a response pattern of graded scores. Psychometrika Monograph, nº 17.

Samejima, F. (1972). A general model for free response data. Psychometrika Monograph, nº 18.

Sancerni, M. D.; Meliá, J. L. y González-Romá, V. (1990). Formato de respuesta, fiabilidad y validez en la medición del conflicto de rol. Psicológica, 11, 167-175.

Tomás, J. M. y Oliver, A. (1998). Efectos de formato de respuesta y método de estimación en el análisis factorial confirmatorio. Psichotema, 10, 197-208.

Vale, C. D. y Weiss, D. J. (1977). A comparison of information fuctions of multiple choice and free parameters vocabulary items. Research Report 77-2. Minneapolis: Psychometric Methods program. Department of Psychology. University of Minnesotta.