Psicothema was founded in Asturias (northern Spain) in 1989, and is published jointly by the Psychology Faculty of the University of Oviedo and the Psychological Association of the Principality of Asturias (Colegio Oficial de Psicología del Principado de Asturias).
We currently publish four issues per year, which accounts for some 100 articles annually. We admit work from both the basic and applied research fields, and from all areas of Psychology, all manuscripts being anonymously reviewed prior to publication.
Psicothema, 2000. Vol. Vol. 12 (Suplem.2). 403-407
Juan C. Oliver*, Jesús Rosel* y Leigh Murray**
* Universidad Jaume I y ** New Mexico State University
Algunas de las deficiencias del análisis de varianza para medidas repetidas son la existencia de estadísticos F sesgados con matrices de covarianza no esféricas, y con distribuciones no exactas en diseños no balanceados. Además, las diferencias individuales en el desarrollo en diseños longitudinales son relegadas al término de error. El trabajo presenta mediante dos estudios de casos las oportunidades surgidas en la solución de estos problemas mediante la metodología de inferencia por máxima verosimilitud. La evidencia existente sugiere que ésta permiten realizar análisis más ajustados mediante el modelado preciso de la matriz de covarianzas, a la vez que proporciona estimadores con propiedades asintóticas conocidas y favorables cuando existen valores perdidos. Permiten también cuantificar la variabilidad interindividual en el desarrollo mediante la estimación de nuevos componentes de varianza, dando respuesta a algunas cuestiones planteadas por Barlow y Hensen en su crítica a la psicología experimental clásica. Se discute por último algunas desventajas y precauciones a tomar en el uso de estos métodos, así como algunas características de los programas informáticos disponibles.
Maximum likelihood analysis of repeated measures. Biased tests and non-exact F distributions are deficiencies in the classical ANOVA approach to repeated measures in the case of non-spherical variance covariance matrices or unbalanced data. Individual differences in developmental patterns have also been typically ignored by being shoved into the error term. This paper discusses two case studies that illustrate analysis opportunities in the solution of these problems by using maximum likelihood methods. Evidence suggests that the latter allow for more precise inference by using more accurate models of the covariance matrix. They also provide estimators with known and favorable asymptotic properties in the case of unbalanced data. Individual differences in growth can be quantified by inclusion of new covariance parameters, which provide some answers to Barlow and Hensen critical remarks on classical experimental psychology. Some potential problems in the use of these methods and characteristics of available software are finally discussed.
En el análisis de experimentos con medidas repetidas ocurre con cierta frecuencia que la matriz de covarianzas no se ajusta al supuesto restrictivo de esfericidad en el análisis de varianza, o de igualdad de varianzas para cualquier par de diferencias entre tratamientos (Huyhn & Feldt, 1970). Una condición suficiente para el cumplimiento de este supuesto se da cuando las variables aleatorias están igualmente correlacionadas y tienen varianzas iguales. Situaciones experimentales comunes provocan sin embargo que las medidas repetidas con mayor contigüidad temporal o espacial presenten correlaciones más altas. Esto puede producirse por ejemplo debido a la fatiga del participante en el estudio sometido a una variedad de tratamientos u observaciones sucesivas. En registros psicofisiológicos tales como potenciales evocados, la cercanía entre dos o más electrodos en el cuero cabelludo permite que éstos detecten procesos psicológicos comunes que conduzcan a una mayor correlación entre aquéllos que entre electrodos más distantes. Estas situaciones generan matrices de covarianzas que incumplen el supuesto de esfericidad y pruebas F sesgadas que inflan la probabilidad a de rechazar la hipótesis nula cuando es cierta por encima del criterio fijado por el investigador.
Tradicionalmente se han propuesto dos soluciones que pueden ser familiares al lector: la utilización de una prueba F con grados de libertad ajustados (Greenhouse & Geisser, 1959), y el análisis de varianza multivariado (O´Brien & Kaiser, 1985). Esta última estrategia es típicamente recomendada cuando existe una grave desviación del supuesto de esfericidad y la muestra sea grande (Jensen, 1982, 1987; Marcucci, 1986). El modelado de la matriz de covarianza mediante procedimientos de estimación de máxima verosimilitud nos lleva a una tercera estrategia que incorpora en el análisis información parámetrica más ajustada al estudio del comportamiento de interés (Wolfinger, 1993). Esta última opción ha mostrado tener más potencia estadística que la prueba F con grados de libertad ajustados en el caso de matrices de covarianza autorregresivas (Albohali, 1983; Milliken & Johnson, 1994), así como resultados favorables más parsimoniosos que el análisis multivariado de varianza (Elston & Grizzle, 1962). El objetivo de la presente comunicación es presentar dos estudios de casos que ilustren las oportunidades y problemas de esta tercera vía en el análisis de medidas repetidas, así como describir algunas características de los programas informáticos disponibles.
Caso I
El estudio consiste en evaluar el efecto sobre la resistencia muscular de tres programas de entrenamiento físico (Littell, Freund & Spector, 1991). En el primero de ellos, se aumentó semana a semana el número de repeticiones de un ejercicio de levantamiento de pesas. En el segundo programa, se aumentó el peso a levantar según los sujetos ganaban en resistencia. En la tercera condición de control, los participantes no hicieron el ejercicio. Las medidas de resistencia se realizaron en días alternos durante un período de dos semanas.
El modelo lineal para un análisis de varianza univariado puede ser expresado como:
yij = µik + sj + eijk (1)
para i = 1, 2, 3 programas de entrenamiento
y k = 1, 2,.....,7 días alternos y j = 1, 2,..., ni sujetos por programa.
en donde ![]() y ambos son independientes. La matriz de covarianzas puede expresarse como:
y ambos son independientes. La matriz de covarianzas puede expresarse como:
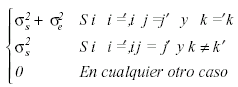
o equivalentemente:
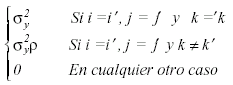
Contando en ambos casos con dos parámetros. Podemos formular las hipótesis estadísticas de efectos principales de Programa (H01 ), y Tiempo (H02), así como la interacción entre Programa y Tiempo (H03) del modo siguiente:
H01 : µ1.. = µ2..= µ3..
H02 : µ..k = µ..k’ para cualquier par de tiempos k, k’
H03 : µi.k - µi.k’ = µi.k - µi.k’ para cualquier par de programas i, i’ y de tiempos k, k’
Sus resultados pueden apreciarse en la Tabla 1, resultando significativa la interacción entre programa y tiempo, pero no así el efecto principal de programa.
Un diagnóstico de la adecuación del modelo mediante el análisis de residuales revela la siguiente matriz de correlaciones, con valores decrecientes en función de la distancia temporal entre observaciones.
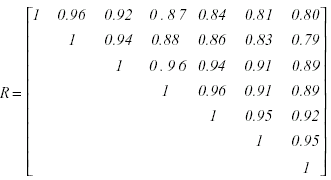
La inspección visual nos sugiere un mal ajuste al criterio de esfericidad. Esto es apoyado por los resultados de la prueba de Mauchly, así como por el valor ε de Geisser-Greenhouse estimado en 0.42, que se aleja del valor 1 requerido por la prueba F insesgada para los contrastes intrasujetos. A la vista del tamaño de la muestra (N = 57), y de la desviación considerable respecto de la condición de esfericidad, podemos considerar la alternativa del análisis multivariado.
El modelo lineal en este caso puede expresarse como:
Y = X β + E (2)
en donde Y es la matrix de observaciones (Sujetos x Tiempos)
X es la matriz del diseño (Sujetos x Programas)
β es el vector de parametros de efectos fijos o medias (Programas x Tiempos)
E es la matriz de diferencias individuales (Sujetos x Tiempos)
y ![]()
La matriz de covarianzas en este caso no tiene restricciones, por lo que cuenta con 28 parámetros distintos, 7 varianzas y 21 covarianzas.
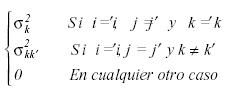
El contraste de las hipótesis para los efectos intrasujetos equivalentes al modelo univariado ha de realizarse mediante contrastes multivariados. La hipótesis lineal general multivariada viene dada por:
H0 : H β M' = 0
En donde H es la matriz de contrastes esperimentales de interés para los tratamientos entresujetos, y M es la matriz de combinaciones lineales intrasujetos o entre tiempos de interés. Podemos expresar así las hipótesis estadísticas de efecto principal de tiempo (H02), e interacción entre tiempo y tratamiento (H03 ) como:
H03 : HPROG β M'T = 0
siendo HINT un vector 1 x 3 de unos, HPROG la matriz 2 x 3 de hipótesis de efecto principal de programa expresada de forma matricial, y MT la matrix 6 x 7 de hipótesis de efecto principal de tiempo. Estos contrastes son programados por defecto a través de los comandos de medidas repetidas en paquetes estadísticos usuales tales como Statistical Package for the Social Sciences (SPSS) o Statistical Analysis System (SAS). En los resultados en la Tabla 2 no se aprecian cambios considerables en cuanto al efecto principal de tiempo, mientras que la interacción entre programa y tiempo ha dejado de ser significativa.
Una segunda alternativa al modelo univariado clásico consiste en utilizar un modelo univariado autorregresivo. Aunque podemos expresar el modelo lineal como en la ecuación (1), la diferencia radica en la matriz de covarianzas. Esta cuenta también con dos parámetros, pero indica una correlación decreciente en función de la distancia temporal de las observaciones (d):
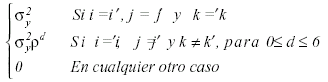
La programación en SAS del procedimiento de análisis mediante métodos de máxima verosimilitud puede consultarse en el Anexo A, y el resultado en la Tabla 3. La fundamentación teórica de los estadísticos utilizados en el contraste de estos efectos intrasujeto es expuesta en Littell, Milliken, Stroup & Wolfinger (1996).
Los métodos de máxima verosimilitud nos permiten también contrastar el ajuste de las tres matrices de covarianza utilizadas en los modelos anteriores. Como puede verse en la Tabla 4, los criterios de Akaike y Schwarz son más cercanos a cero en el caso de la matriz autorregresiva, lo que suele considerarse como un índice de mejor ajuste (Littell, Milliken, Stroup & Wolfinger, 1996). Este modelo es además más parsimonioso en cuanto que parece conseguir mejores resultados con un ahorro de 26 parámetros respecto de la matriz de covarianzas multivariada sin restricciones. Aunque todavía faltan más trabajos de investigación en este sentido, los resultados citados anteriormente (Elston & Grizzle, 1962; Albohali, 1986) apuntan al valor de una precisa especificación de la matriz de covarianzas y por lo tanto favorecerían también al último modelo.
Caso 2
Una deficiencia de la metodología tradicional del análisis de varianza en la investigación longitudinal es que no modela explícitamente las diferencias individuales en patrones de crecimiento, relegándolas al término de error. Asume también la existencia de un diseño completo con el mismo número de observaciones por persona y espaciamiento temporal, considerando al factor de medidas repetidas como cruzado al factor sujetos. Cuando existen datos faltantes puede ocurrir que algunas razones F en el modelo univariado no tengan distribuciones exactas, y sólo sean aproximaciones que empeoran conforme aumenta el número de valores perdidos (Milliken & Johnson, 1994). En el análisis de varianza multivariado, los paquetes estadísticos comunes tales como SAS o SPSS eliminan cualquier registro incompleto antes de ejecutar los algoritmos de cálculo. Los procedimientos de máxima verosimilitud se presentan como alternativas en este sentido cuando existen muestras grandes. Permiten además considerar las medidas repetidas como anidadas al factor sujeto, con un número desigual de observaciones por persona y distinto espaciamiento temporal. Incorporan también parámetros de variabilidad interindividual en crecimiento, cuya estimación tiene en cuenta las diferentes precisiones derivadas del distinto número de medidas hechas en cada participante.
Los datos del siguiente ejemplo simulan un estudio longitudinal del desarrollo de la lectura en función de la edad. El modelo intra sujetos puede ser expresado como
yik = b0i + b1i tik + eik para i = 1,2,...,n niños y t = 0,1,...,k-1 ocasiones (3)
siendo b0i el nivel de lectura inicial al comienzo del estudio, y b1i la pendiente de crecimiento personal para el individuo i. Si expresamos t como puntuaciones diferenciales respecto de la media de la variable tiempo, b0i puede ser interpretado como la media de niveles de lectura para cada sujeto en todos sus registros. Estos valores de la ecuación individual forman parte del modelo entresujetos
en donde b0i = β0 + αm + d0i, y b1i = β1 + γm + d1i (4)
para m = 1, 2 métodos de enseñanza de la lectura.
Siendo β0 y β1 los parámetros poblacionales de media de lectura inicial y pendiente de asociación entre nivel de lectura y edad, αm y γm son los efectos de método de enseñanza sobre el nivel de lectura medio y sobre la pendiente. Las desviaciones aleatorias individuales respecto de los valores poblacionales de constante y pendiente vienen expresadas por d0i y d1i, respectivamente. Se asume además las siguiente distribución de efectos aleatorios del modelo:
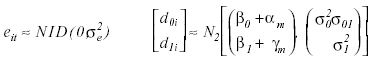
En donde σ2e indica la variabilidad de las observaciones intrasujetos con respecto a los valores predichos en la ecuación individual. Los nuevos parámetros σ20, σ21 y σ01 reflejan las varianza entresujetos de nivel inicial de rendimiento en lectura, la varianza de las pendientes de asociación entre nivel inicial de lectura y edad, y la covarianza entre estos dos coeficientes de regresión aleatorios. Una exposición detallada de procedimientos de estimación y contraste de hipótesis respecto de estos nuevos parámetros puede consultarse en Goldstein (1995). La Figura 1 ilustra el caso de efectos significativos en estos tres parámetros, al representar las ecuaciones individuales de desarrollo lector bajo los dos métodos de enseñanza. Las diferencias entre los coeficientes aleatorios de medias y pendientes entre sujetos puede apreciarse en el gráfico, así como el efecto de abanico divergente que expresa una covarianza positiva entre los mismos; es decir, la pendiente de las ecuaciones individuales tienden a aumentar cuando también lo hace la media. El Anexo B incluye un programa con el módulo estadístico SAS que permite realizar este análisis.
Conclusión
Se han descrito tres ventajas de los procedimientos inferenciales de máxima verosimilitud en el análisis de medidas repetidas. En primer lugar, éstos permiten una flexible especificación de la matriz de covarianzas que, como vimos en el Caso 1, pueden afectar substancialmente los resultados aun cuando no varíen ni el número de parámetros de efectos fijos (medias) ni las hipótesis contrastadas. En segundo lugar, proporciona procedimientos con más solidez estadística para el tratamiento de valores perdidos. En tercer lugar, permiten la especificación de nuevos componentes de varianza para describir las diferencias individuales en patrones de crecimiento relegados al término de error por los métodos clásicos. Esto puede ser de utilidad para la detección de poblaciones específicas en cuanto a curvas de crecimiento o aprendizaje y para la elaboración de estrategias clínicas o educativas más ajustadas. Son además una buena herramienta en el estudio de los efectos de variables contextuales sobre el desarrollo. Las posibilidades de inferencia sobre la descripción de comportamientos individuales de los participantes en el estudio proporciona así algunas soluciones a las críticas planteadas por Barlow y Hensen (1984) a la psicología experimental clásica.
Como inconvenientes de la utilización de procedimientos de máxima verosimilitud cabe señalar en primer lugar la necesidad de muestras grandes de las que dependen las buenas propiedades de los estimadores. En segundo lugar la aparición de resultados con componentes negativos de varianza que puede deberse a observaciones inusuales, problemas en el diseño o a una mala especificación del modelo, pero que crea en cualquier caso problemas de interpretación (Smith & Murray, 1984; Hocking, 1996). En tercer lugar surgen preguntas sobre la estabilidad de las soluciones de los estimadores encontradas, que dependen de la ejecución de los algoritmos de búsqueda de máximos en la función de verosimilitud. Puede ser posible que los máximos encontrados sean locales y no globales, por lo que la repetición del procedimiento desde otros puntos de partida resultará en estimadores con valores distintos (Searle, Casella & McCulloch, 1992). Estas preguntas reflejan la complejidad de estos procedimientos, por lo que su utilidad para la realización de inferencias sobre el comportamiento puede depender de que su uso esté basado en una adecuada formación.
Anexo A
Programación en SAS del modelo con matriz de covarianza autorregresiva
PROC MIXED;
CLASS PROGRAMA TIEMPO SUJETO;
MODEL RESIST = PROGRAMA TIEMPO
PROGRAMA x TIEMPO;
REPEATED / SUB= SUJETO TYPE=AR(1);
Nota: La sintaxis de este procedimiento es similar a la utilizada en el modelo lineal general en el anterior ejemplo. Sin embargo, el comando REPEATED es utilizado aquí para la especificación de la variabilidad intrasujeto. El subcomando SUB = SUJETO indica que esta será de bloques en diagonal definidos por cada identificador de este último factor. El subcomando TYPE = AR(1) especifica la estructura de covariación entre las observaciones dentro de cada bloque, que en este caso será autorregresiva de orden 1.
Anexo B
Programación en SAS del modelo con coeficientes aleatorios para el análisis del diseño longitudinal
PROC MIXED;
CLASS SUJETO METODO;
MODEL LECTURA = TIEMPO METODO
METODO x TIEMPO;
RANDOM INTERCEPT TIEMPO / SUB=SUJETO
TYPE=UN;
Nota: El comando RANDOM refleja aquí la variabilidad entre sujetos de los coeficientes aleatorios. La identidad de los sujetos es definida mediante el comando SUB, mientras que el comando TYPE=UN especifica una matriz de covarianzas no restringida de orden 2 x 2 entre los coeficientes individuales.
Albohali, M.N. (1983). A time series approach to the analysis of repeated measures designs. Ph. D. Dissertation. Kansas State University.
Barlow, D. M. & Hensen, M. (1984). Single case experimental designs: strategies for studying behavioral change (2nd ed.). Nueva York: Pergamon.
Elston, R. C. & Grizzle, J. E. (1962). Estimation of time-response curves and their confidence bands. Biometrics, 18, 148-159.
Goldstein, H. (1995). Multilevel Statistical Models (2nd. ed.). London: Arnold.
Greenhouse, S. W. & Geisser, S. (1959). On methods in the analysis of profile data. Psychometrika, 24: 95-112.
Hocking, R.R. (1996). Methods and applications of linear models. New York: Wiley.
Huyhn, H. y Feldt, L. S. (1970). Conditions under which mean square ratios in repeated measures designs have exact F-distributions. Journal of the American Statistical Association, 65, 1582-89.
Jensen, D. R. (1982). Efficiency and robustness in the use of repeated measurements. Biometrics, 38, 813-825.
Jensen, D. R. (1987). Topics in the analysis of repeated measurements. In H. Bozdogan & A. K. Kupta (Eds.), Multivariate statistical modeling and data analysis (pp. 147-161). New York: Wiley.
Littell, R. C., Freund, R.J. & Spector, P.C. (1991). SAS System for Linear Models (3rd ed.). Cary NC: SAS Institute.
Marcucci, M. (1986). A comparison of the power of some tests for repeated measurements. Journal of Statistical Computation and Simulation, 26,37-53.
Milliken, G. A. & Johnson, D. (1994). Analysis of messy data. Vol 1: Designed Experiments. London: Chapman Hall.
O’Brien, R. G. & Kaiser, M. K. (1985). MANOVA method for analyzing repeated measures designs: An extensive primer. Psychological Bulletin, 97, 316-333.
Searle, S. R., Casella, G. & McCulloch, C. W. (1992). Variance components. New York: John Wiley.
Smith, D. W. & Murray, L. W. (1984). An alternative to Eisenhart´s model II and mixed model in the case of negative variance estimates. Journal of the American Statistical Association, 79, 145-151.
Wolfinger, R. (1993). Covariance structure selection in general mixed models. Communications in statistics: Simulation, 22 (4), 1.079-1.106.