Psicothema was founded in Asturias (northern Spain) in 1989, and is published jointly by the Psychology Faculty of the University of Oviedo and the Psychological Association of the Principality of Asturias (Colegio Oficial de Psicología del Principado de Asturias).
We currently publish four issues per year, which accounts for some 100 articles annually. We admit work from both the basic and applied research fields, and from all areas of Psychology, all manuscripts being anonymously reviewed prior to publication.
Psicothema, 2000. Vol. Vol. 12 (Suplem.2). 423-426
Manuel Pelegrina*, Francesc Salvador Beltrán** y Mercedes Ortiz*
* Universidad de Málaga y ** Universidad de Barcelona
La información organizada en esquemas de conocimiento requiere la categorización del material de la prueba: letras, sílabas, palabras, frases, dibujos, etc., antes de ser sometida a tareas de atención, memoria, percepción, etc. Una de las técnicas ha consistido en el escalamiento subjetivo del estímulo mediante escalas de estimación (v.g. Torgerson, 1958). Por otra parte, la aplicación de escalas de estimación ha resultado ser una técnica muy útil en procedimientos aplicados en la teoría de la detección de señales (TDS) y en la obtención de curvas características operativas del receptor (ROC) que representa los datos mediante escalas ordinales. Esta técnica ha llegando a constituir una forma natural de categorización para la estimación de curvas ROC (Metz, Herman y Shen, 1998). Nuestro objetivo consiste en presentar un modelo de categorización aplicado en acciones organizadas de forma esquemática. Esta categorización representa un primer nivel para el escalamiento de la información. Un segundo nivel en el que se aplican índices de sensibilidad adecuados y un tercer nivel de representación y valoración de los modelos obtenidos. Ya que hemos realizado investigaciones iniciales en torno al primer y segundo nivel (v.g. Pelegrina, Salvador y Buil, 1997), en el presente trabajo trataremos sobre las posibilidades analíticas y de modelización cuando estos datos son considerados o analizados desde el análisis ROC. Este tipo de análisis se ha aplicado de una forma sistemática en contenidos biomédicos más que en psicología (v.g. Zou y Hall, 1997). No obstante, este procedimiento es un modelo de representación de los datos complementario entre las teorías del esquema y la TDS.
Categorization of schematic organized information by means of ROC curves. The information organized in knowledge schemes (scripts) needs to be studiet by techniques in which elements are categorized as test material: Letters, syllables, words, sentences, pictures, etcetera. One of these techniques considers subjective scaling of the stimulus by means of rating scales (v.g. Torgerson, 1958). Furthemore, the application of rating scales has been a very useful technique applied in signal detection theory (SDT). With this technique it is possible to get the receiver operating characteristic or ROC curve. That curves represents ordinal data. This technique constitutes a natural categorization for estimations of ROC curves. On the other had, the presentation of one model of categorization applied to events included in the scheme. The categorization represents a first level to escale the information. A second level is the suitable application of indices of sensitivity. The third level is the statistical modelling. We have carried out initial research at the first an second level (v.g. Pelegrina, Salvador y Buil, 1999). In the present work we are analized possibilities of modelling when the data are considered or analiyzed by means of ROC analysis. This technique has been largely used in biomedical research(radiology)unlike psychology (v.g. Zou y Hall, 1997). However, this is a model of data representation complementary between the scheme theory and the SDT.
En un modelo basado en la teoría de la detección de señales partimos del supuesto de que los aciertos y rechazos incorrectos, así como las falsas alarmas y los rechazos correctos son complementarios entre sí respectivamente. Sin embargo, en tareas en las que intervienen variables o procesos de cierta complejidad (v.g. memoria de palabras o frases, adquisición de conceptos, discriminación-decisión), los datos ofrecen a menudo evidencia sobre lo contrario; es decir, aparecen datos no complementarios entre sí. Ello ha dado lugar a que además de d’ apliquemos una serie de índices diferenciados (η, Q, etc.) en función de la naturaleza de los datos y ello tenga un reflejo también en el tipo de curvas ROC utlizadas (v. g. Castro et al. 1997; Egan, 1975; Metz, Herman y Shen, 1998; Pelegrina y Salvador, 1989 y Swets, 1986). Ejemplos de lo anterior los hemos venido representando en nuestros trabajos anteriores (Pelegrina, 1988,1997). Así, en el cuadro 1 observamos una tabla de contingencia en un diseño en el que se obtienen datos sobre el «acuerdo» o «desacuerdo» ante dos tipos de información denominada «señal» y «ruido» en terminología clásica y que en el cuadro indicado representa información que el sujeto ha de discriminar «señal» frente a otro tipo de información de las mismas características denominada «ruido». Los datos que hemos venido obteniendo con este tipo de información (v.g. Pelegrina 1988; Pelegrina y Salvador, 1988), indican que las categorías o variables con un significado alto (tipicidad alta, frecuencia de uso alta, etc.) se discriminan menos que la información atípica (Pelegrina, Gallifa, y Beltran, 1994).
Mediante los datos obtenidos podemos calcular los índices más adecuados. Algunos de los cuales son consistentes con la existencia de criterio de decisión, otros son consistentes con la existencia de umbral sensorial y, finalmente, otros no presuponen modelo alguno, sino procesos puramente aleatorios.
Entre los índices consistentes con la existencia de criterio de decisión se encuentra d’, típica de la TDS, índice de sensibilidad paramétrico, enormemente estable y sensible que se define como la diferencia de medias entre dos distribuciones normales solapadas respecto a la señal y al ruido, dada en desviaciones típicas:
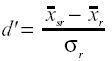 (1)
(1)
donde d’ es un índice de sensibilidad, ![]() sr -
sr - ![]() r
es la diferencia de medias entre la distribución de la señal y
el ruido y σr es la desviación típica
del ruido, d’ mide la sensibilidad del sujeto en el proceso sensorial
y se ve afectada por variables relacionadas con el proceso sensorial y no por
el criterio de decisión, en el que influyen otros tipos de variables.
Esta fórmula considera la desviación típica del ruido como
elemento de error. Pero el error, en el ámbito de la recuperación
de información, puede proceder también de la energía necesaria
para que exista señal y no sólo del ruido, por lo cual se ha propuesto
la fórmula siguiente:
r
es la diferencia de medias entre la distribución de la señal y
el ruido y σr es la desviación típica
del ruido, d’ mide la sensibilidad del sujeto en el proceso sensorial
y se ve afectada por variables relacionadas con el proceso sensorial y no por
el criterio de decisión, en el que influyen otros tipos de variables.
Esta fórmula considera la desviación típica del ruido como
elemento de error. Pero el error, en el ámbito de la recuperación
de información, puede proceder también de la energía necesaria
para que exista señal y no sólo del ruido, por lo cual se ha propuesto
la fórmula siguiente:
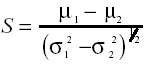 (2)
(2)
donde µ1, µ2, σ21 y σ2 2 y son las medias y las varianzas respectivamente de dos conjuntos de información diferentes (Brookes, 1968).
Por su parte Luce (1963) propone el índice η que no sólo incorpora A(a) y FA(c), como ocurre con d’, sino las cuatro posibilidades de respuesta incluidas en la matriz 2x2, es decir: a,b,c,d. Por ello, este índice permite incorporar datos empíricos asimétricos (o no complementarios entre sí) obtenidos en la matriz de respuestas (cuadro 1):
η = [P(NO/s) x P(SI/r) / (P(SI/s) x (PNO/r)]1/2 =
= b x c / a x d (3)
donde el numerador corresponde a los errores y el denominador a los aciertos. Hay, sin embargo, otras medidas que son compartidas por los cálculos propios de las tablas de contingencia dentro de los modelos categóricos. En efecto, podemos observar otros índices en la tabla 1.
Los índices anteriores representan una serie de posibilidades analíticas que nos permiten utilizar técnicas de análisis diferentes en función de la teoría, la hipótesis y de los datos obtenidos. Debido a ello, unos incluyen solo una parte de la matriz de respuesta, otros permiten relaciones cruzadas y, finalmente, otros utilizan los valores marginales. Dado todo lo anterior, nuestro interés en este trabajo va dirigido a seleccionar los índices más adecuados para representar el proceso de discriminación mediante información organizada de forma esquemática. El proceso anteriormente descrito se resume en tres fases sucesivas que presentamos en los apartados restantes de esta investigación: categorización de la información esquemática, su medida mediante índices y su representación mediante curvas ROC. Ello aplicado a categorías altamente significativas organizadas de forma esquemática (v.g. categorías altamente típicas de un esquema) permite suponer que la discriminación será mínima debido a un exceso de información redundante que producirá interferencia. La constatación empírica de esta hipótesis nos permitirá, en el contexto de la adquisición del conocimiento, determinar las dificultades en la discriminación y en la comprensión de aquellos conceptos que reúnen dos características básicas: son importantes y están muy relacionados entre sí. Así, si nos situamos en el ámbito de adquisición del conocimiento (tipo clase magistral) podemos considerar dos clases de información: la información que presentamos a los alumnos (señal) y aquella que no presentamos (ruido). Por consiguiente, frente a una posible evaluación de la adquisición del conocimiento debemos diferenciar entre información presentada que realmente se ha de conocer frente a información no presentada por el profesor o no adecuada respecto al concepto. La primera la hemos operacionalizado como señal y la segunda como ruido.
Método
Sujetos
Los datos proceden de una muestra de 83 sujetos que cursaban la asignatura de Metodología de las Ciencias del Comportamiento de la Facultad de Psicología (Universidad de Málaga). Los sujetos eran hombres y mujeres de edad comprendida entre 18 y 22 años.
Material
Se utilizó una plantilla de recogida de datos generada por 201 sujetos (Pelegrina, et al. 1999).
Procedimiento
Se realizó una tarea típica de memoria de reconocimiento. En primer lugar se pasó una lista de contenidos propios de las asignaturas de metodología (Pelegrina, et al. 1999) La tarea consistió en leer lo más rápidamente posible las frases. El tiempo de lectura, fijo para todos los sujetos, fue de 24 segundos. Se calcularon dos segundos para cada uno de los conceptos. Pasada una semana, a la misma hora, se pasó el cuestionario (Pelegrina et al. 1999). Cada alumno/a contestó «SÍ» o «NO» y añadió su seguridad en la respuesta mediante una escala de estimación de uno a cinco, donde cinco indicaba el mayor nivel de seguridad. Esta prueba se realizó sin límite de tiempo.
Resultados y discusión
Los resultados obtenidos se presentan en la curva ROC de la figura 1 y en la tabla 2. En ellas se observa que a pesar de haber presentado el mismo número de señales y ruidos, sin embargo las respuestas no han sido igualmente repartidas. Ello indica que es inadecuado aplicar una d’ . Es necesario elegir, entre los índices presentados en la introducción, aquel o aquellos que incluyan todos los valores obtenidos: a , b , c y d. Uno de los posibles es el índice η. No obstante, el log of ratio también incluye todos los valores, pero dada la variabilidad de los datos no es necesario aplicar el logaritmo. Por su parte la Q de Yule, que también incorpora las cuatro posibilidades de respuesta, «penaliza» de una manera excesiva los errores, dados los datos que hemos obtenido. Por razones teóricas no se han incluido los índices de umbral, ya que se supone que en las tareas que hemos venido aplicando en este experimento influyen más procesos relacionados con la memoria que procesos relacionados con el umbral sensorial. Finalmente, en relación al coeficiente phi, éste se encuentra más relacionado con hipótesis sobre las que debemos obtener un índice de asociación entre las variables. Por todo lo anterior, hemos elegido el índice η que además se incluye entre los que permiten, en caso de ser neceario para la hipótesis, un control del criterio de decisión de acuerdo con la propuesta de Wald (1950).
El perfil de los datos muestra que ha habido muchos aciertos pero también muchas falsas alarmas, respuesta típica de aquellas categorías que siendo similares entre sí representan además un alto nivel de información (v.g. Pelegrina, 1988). Por otra parte, la correlación de Spearman no proporcionó ninguna relación estadísticamente significativa y el valor η fue de 0.22 , el cual indica que los aciertos (respuestas a y d) son levemente superiores a los errores. Por su parte, la curva ROC de la figura 1 representa valores propios de una distribución próxima al azar. Por lo que podemos considerar que la discriminación ha resultado ser prácticamente nula. Debido a lo anterior, entre los índices que hemos presentado en la introducción del presente trabajo, hemos elegido η, ya que permite valorar todas las respuestas de los sujetos: SÍ-NO más escala de estimación, tanto con la presencia del concepto como con su ausencia (ver tabla 2).
Los resultados aquí obtenidos mostraron una discriminación muy pequeña si observamos el índice η obtenido y la curva ROC, aunque son consistentes con los obtenidos anteriormente en otro contexto (Pelegrina, Gallifa, y Beltran, 1994). Sus implicaciones en la adquisición del conocimiento esquemático indican que los sujetos muestran un cierto efecto de suelo debido a que la manipulación experimental ha dado lugar a un incremento alto de información típica, así como a un intervalo alto de retención. En un sentido aplicado ello indica que cuando se presenta mucha información relevante es necesario crear distintividad entre los conceptos similares con tal de que los alumnos puedan llevar a cabo una adquisición de conceptos importantes y relacionados; pero a su vez desarrollen una alta discriminabilidad entre ellos.
Brookes, B.C.(1968). The measures of information retrieval effectiveness proposed by Swets. Journal of Documentation, 24 (1), 41-54).
Castro, M., Ruiz, M., Pelegrina, M., López, E., Luna, R., y Videra, A. (1997, septiembre). Race categorization of human faces: Assessment from signal detection theory. Póster presentado en la 4th European Conference on Psychological Assessment.Lisboa. Entidad organizadora: European Association of Psychological Assessment. Carácter: Internacional.
Egan, J. P. (1975). Signal detection theory and ROC analysis. New York: Academic Press.
Luce, R.D.(1963). Detection and recognition. In the R.D. Luce, R.R. Bush & E. Galanter (Eds.). Handbook of mathematical psychology I (pp. 103-189). New York: Wiley.
Metz, C. E., Herman, B. A. y Shen, J. (1998). Maximum likelihood estimation of receiver operating characteristic (ROC) curves from continuosly-distributed data. Statistic in Medicine, 17, 1.033-1.053.
Pelegrina, M. (1988). Procesos de comprensión y esquemas de conocimiento: adquisición, desarrollo y organización en el niño[Microficha]. Barcelona. Publicaciones Universidad de Barcelona. Departamento de Metodología de las Ciencias del Comportamiento. Psicología Experimental-Metodología (Tesis doctorales publicadas en microficha).
Pelegrina, M.(1997, septiembre). Categorización de esquemas mediante detección de señales. Comunicación presentada en el V Congreso de Metodología de las CC del Comportamiento. Sevilla. Entidad organizadora: Asociación Española de Metodología de las Ciencias de Comportamiento. Carácter: Nacional.
Pelegrina, M., Gallifa, J., y Beltran, F. (1994) Typical and atypical information as structural categories in the instructional processes. Perceptual and Motor Skills. 79, 1.319-1.324.
Pelegrina, M., Ruiz, M., López, E., Ortiz, M., y Videra, A. (1999, septiembre). Mejoras obtenidas en el rendimiento de asignaturas metodológicas mediante la participación de los alumnos. Póster presentado en las «Jornadas de proyectos de Innovación educativa Universitaria sobre Mejora de la Práctica Docente» (ICE). Universidad de Málaga.
Pelegrina, M., y Salvador, F.(1989, Septiembre).Curvas ROC y procesos de discriminación y decisión en memoria: efectos de tipicidad. Comunicación presentada en la «2ª Conferencia Española de Biometría». Segovia. Entidad organizadora: Grupo Español de la Biometric Society. Carácter: Nacional.
Swets, J. A. (1986). Indices of discrimination or diagnostic accurancy: Their ROCs and implied models. Psychological Bulleting, 99 (1), 100-101.
Torgerson, W.S.(1958). Theory and methods of scaling. Nueva York: Wiley.
Zou, K. H. y Hall, W. J. (1997). Semiparametric and parametric transformation models for estimating a receiver operating characteristic (ROC) curve from continuous diagnostic test data. Technical Report.
Wald, A. (1950). Statistical decisions functions. New York: Wiley.
Weber, E.U.(1988). Exoectation and variance of item resemblance distributions in a convolution-correlation model os distributed memory. Journal of Mathematical Psychology, 32, 1-43.