Psicothema was founded in Asturias (northern Spain) in 1989, and is published jointly by the Psychology Faculty of the University of Oviedo and the Psychological Association of the Principality of Asturias (Colegio Oficial de Psicología del Principado de Asturias).
We currently publish four issues per year, which accounts for some 100 articles annually. We admit work from both the basic and applied research fields, and from all areas of Psychology, all manuscripts being anonymously reviewed prior to publication.
Psicothema, 1990. Vol. Vol. 2 (nº 2). 189-209
Guillermo Vallejo y Paula Fernández
Departamento de Psicología. Universidad de Oviedo.
SOFTWARE, INSTRUMENTACIÓN Y METODOLOGÍA
Los diseños de medidas repetidas han sido tradicionalmente analizados por medio del univario modelo mixto del AVAR, sin embargo, cuando los tratamientos no son presentados en un orden aleatorio la secuencialidad de los registros introduce correlación en los errores del modelo. Bajo la asunción de que la correlación sería¡ puede ser modelada mediante procesos ARMA relativamente simples, este trabajo considera el problema de obtener estimadores eficientes y consistentes. Para concluir se presenta un ejemplo que ilustra el procedimiento descrito.
Palabras clave: Diseños de medidas repetidas, diseños longitudinales, análisis de series de tiempo, errores autocorrelacionados, modelo mixto del AVAR.
Repeated measures designs with autocorrelated errors.- The repeated measures designs lave been traditionally analyzed using the univariate mixed model of AVAR. however when the treatments are not presented in a randomized order, the sequence of observations introdoce correlation in the errors of model. Under the assumption that the serial correlation can be modeled through relatively simple ARMA processes, this paper considers the problem of obtaining efficient and consistent estimators. Finally, a example that illustrates the process that has been described is presented.
Key words: Repeated measures designs, time series analysis, longitudinal designs, autocorrelated errors, mixed model of AVAR.
Los diseños de medidas repetidas constituyen en la actualidad uno de los procedimientos analíticos más ampliamente utilizados dentro de las Ciencias Sociales, Comportamentales y de la Salud. Frecuentemente p muestras o grupos de n bloques de unidades experimentales son aleatoriamente asignadas a los niveles de una variable entre grupos. Seguidamente, la secuencia de administración de los q niveles de la variable intra tratamientos a las unidades experimentales de los p grupos de bloques se contrabalancean para cada uno de éstos. Sin embargo, a menudo ocurre que la presentación aleatoria de los niveles de la variables intra no es utilizada, bien sea porque su propia naturaleza imposibilita al investigador para manipularlos intencionalmente (carácter temporal), o bien sea porque la propia investigación así lo requiera. Sin pretender acotar todas las áreas de las que pueden extraerse ilustraciones de lo dicho, sí vamos a presentar ejemplos de algunas de ellas. Así, a un investigador en el campo del aprendizaje le puede interesar estudiar cómo influye la práctica en las ejecuciones de los sujetos que presentan distinto grado de motivación, a un psicólogo escolar le puede resultar de interés determinar los cambios que se producen en un espacio de tiempo definido en dos muestras de niños tratados con dos métodos distintos de aprendizaje de la lectura, o a un psicólogo clínico le puede interesar investigar la eficacia de un tratamiento especialmente diseñado para mitigar la obesidad en dos grupos de pacientes uno de los cuales sirve de control del otro.
En todos los casos, la dependencia serial entre las observaciones tomadas desde una misma unidad de análisis en distintos momentos o intervalos temporales puede llegar a ser de considerable importancia. Como se ha puesto de manifiesto en distintas investigaciones (Vallejo, 1986), típicamente, las observaciones registradas desde un mismo sujeto, además de estar positivamente correlacionadas, presentan una matriz de varianzas-covarianzas entre las medidas repetidas que tiene una estructura Toeplitz (las puntuaciones más próximas presentan una correlación más elevada). De este modo, este fenómeno es contrario a las asunciones que subyacen al modelo mixto del análisis de la varianza (AVAR) tal y como fue formulado inicialmente por Scheffé en 1956, y aparece implementado en los paquetes estadísticos más usados: BMDP, SPSS y SAS.
Así las cosas, lo que resta de este trabajo, lo dedicaremos a abordar el problema de la ineficacia de los estimadores derivados de la utilización del tradicional modelo mixto del AVAR cuando el supuesto de independencia no es satisfecho. Para cumplir con este objetivo, desarrollaremos un modelo que nos permita obtener estimadores eficientes; aspecto éste, que entre otras muchas ventajas, nos va a conceder atribuir a los tratamientos la importancia que realmente tienen.
2.- Formas que puede adoptar la matriz de varianzas-covarianzas en los diseños de medidas repetidas
Tradicionalmente, el método de análisis de los diseños de medidas repetidas ha consistido en un modelo estructural del AVAR con valores esperados mixtos. En particular, el factor bloque o sujeto se ha considerado aleatorio. Como ha sido discutido por Danford y otros (1960), si yijk representa la kth medida en el ith individuo dentro del jth grupo, la ecuación lineal univariada que subyace al modelo mixto del AVAR con dos factores fijos y uno aleatorio puede ser escrita como sigue:
yijk = μ + αj + βk + πi(j) + (α β)jk + (β π)ki(j) + εijk (2.1)
i =1,..., n ; j = 1, ..., p ; k = 1,..., q
con las condiciones de lado:
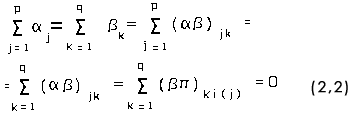
donde:
μ es la media general.
αj es el efecto del jth nivel de tratamiento.
βk es el efecto de la kth medida.
πi (j) es el efecto del ith sujeto medido en el jth nivel de tratamiento.
(α β)jk es el efecto de la jkth interacción.
(β π)ki(j) es el efecto de la interacción de la kth medida con el ith sujeto dentro del jth nivel de tratamiento.
εijk es el componente del error aleatorio.
Dado que para cada sujeto hay asociado en cada kth nivel de tratamiento un vector de q medidas [ yijk ]. Entonces el valor esperado de yijk será igual al promedio de los efectos que en la ecuación (2.1) representan efectos fijos; es decir,
E (yijk) = μjk = μ + αj + βk + (α β) jk (2.3)
denotando la desviación aleatoria yijk de μ jk como mijk el modelo de la ecuación (2.1) adopta la forma:
yijk = μik + mijk (2.4)
donde mijk recoge los componentes aleatorios del modelo para los cuales se asume distribución normal y valor esperado cero; esto es
E (μ ijk) = 0 (2.5)
Y
E (m¡jk m’ ijk) = σ 2 (si i = i, j = j y k= k)
E (mijk m ijk’) = ρ σ2 (si i = i, j = j y k ≠ k) (2.6)
La combinación de estas dos presuposiciones definen un tipo especial de matriz de varianzas-covarianzas que tiene una forma llamada de simetría combinada y que puede expresarse como sigue:
E (mi m'i)= σ2ε ( Iqi - 1 / qi Jqi ) + ( σ2ε + qi σ2π ) 1 / qi Jqi (2.7)
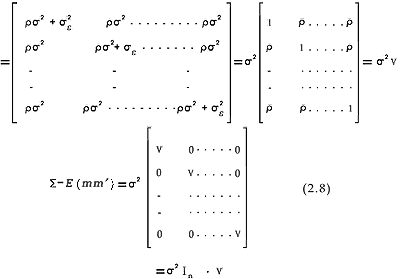
donde
σ2 = σ2ε + σ2π, ρ = σ2π / σ2, I denota una matriz de identidad de orden q y Jq = 1q x 1'q.
Ahora bien, al ser E ( mi m' i , ) = 0 (i ≠ i') se sigue que con las matrices de varianzas-covarianzas asociados con cada nivel de tratamiento j, Σj comunes para todos los p de la población ( Σj = Σ para todo j = 1,..., p).
Geisser y Greenhouse (1958) y Greenheuse y Geisser (1959) al extender el trabajo inicial de Box (1954) con diseños de medidas repetidas de una sola muestra a diseños de medidas repetidas con muestras divididas, pusieron de manifiesto que si las distintas matrices Σ j constituyen muestras al azar de la misma población de matrices de varianzas-covarianzas (para verificar la validez de esta asunción se acude normalmente a la versión multivariada de la prueba de homogeneidad de la varianza de Bartlett descrita por Box en 1950), pero Σ tiene una forma arbitraria entonces los estadísticos asociados con las medidas repetidas [CMB/CMBXS(A) y CMAB/CM BXS(A)] se siguen distribuyendo de acuerdo con la F ordinaria, aunque con [(q-1)ε] / [p (n-1) (q-1)]ε y [(p-1) (q-1)] ε / [p(n-1) (q-1)] ε grados de libertad, donde el factor de corrección ε es un número cuyo valor depende del grado de desviación de la matriz de varianzas-covarianzas de la población de la forma requerida (Winer, 1971). De este modo, si la asunción de simetría de la matriz Σ se constata en los datos experimentales (ε = 1) las razones CMB/CMBXS(A) y CMAB / CMBXS(A) se distribuyen como F con [(q-1) / p (n-1) (q-1)] y [(p-1) (q-1)] / p(n-1) (q-1)] grados de libertad. Sin embargo, conforme Σ se desvía del patrón de simetría requerido, el valor de ε va disminuyendo progresivamente, con un valor mínimo para F aproximadamente igual a 1 / (q -1). Así pues,
FB = F [ ( q - 1 ) ε , p ( n - 1 ) ( q - 1 )ε ]
FAB = F [ ( p - 1 ) ( q - 1 ) ε , p ( n - 1 ) ( q - 1 )ε ]
y
1 / (q - 1 ) ≤ ε ≤ 1 (2.9)
Por lo tanto, es de suma importancia tener en cuenta este hecho, ya que conforme nos desviamos de la condición de uniformidad las razones F se vuelven cada vez más liberales, incrementándose de este modo la posibilidad de capitalizar sobre el azar.
Si examinamos un poco más sustantivamente el contenido formal de la matriz Σ vemos, por un lado, que ésta, al igual que cualquier otra matriz subyacente a un modelo mixto del AVAR, incorpora dentro de sí las desviaciones resultantes de sustraer las puntuaciones de cada uno de los sujetos de las respectivas medias en los diferentes niveles de tratamiento; puntuaciones diferenciadas que como hemos visto en la formalización expresada en (2.7) incluyen tanto la variación submuestral dentro de las unidades experimentales (errores de medida asociados con las distintas observaciones), como la variación aleatoria en el promedio de las respuestas de los diferentes sujetos asignados a los p niveles de tratamiento (errores aleatorios asociados con las unidades experimentales). Y, por otro, que para cada sujeto se asume que los errores son independientes a lo largo de los distintos puntos de observación. Este hecho se deriva directamente del cumplimiento de la condición de simetría combinada, la cual como es sabido implica que las variables aleatorias del modelo están igualmente correlacionadas para todos los pares de observaciones de un mismo sujeto y tienen varianza constante.
Durante bastantes años se consideró que la única matriz que satisfacía el requisito de ε = 1 era la de simetría combinada, sin embargo, Huynh y Feldt (1970) y Rouanet y Lépine (1970) han demostrado que la asunción de uniformidad es tan sólo una condición suficiente, no una condición necesaria para la validez de la razón F univariada en los diseños de medidas repetidas.
Por ejemplo, Huynh y Feldt (1970) han confirmado que las razones F también se distribuyen como F si las diferencias entre las varianzas de cualquier par de tratamiento son iguales; esto es, si
α2djj, = σ2yj - yj' = σ2j + σ2j' - 2σ2j j' =
Cte para todo j y j' (2.10)
Cuando el supuesto de simetría combinada está presente, es obvio que la igualdad anterior se cumple para todos los pares de valores j y j', dado que la matriz de simetría es un caso especial de una condición más general que presentan las matrices en las cuales se mantiene la asunción de igualdad en las diferencias de las varianzas entre dos cualesquiera tratamientos. De este modo, la igualdad de las varianzas y de las covarianzas no es requerida para que el estadístico F se comporte conforme a la distribución F, la condición necesaria y suficiente para la validez de la razón F es que la matriz Σ sea circular o esférica. Este aspecto se cumple sí Y sólo sí la matriz de varianzas-covarianzas Σ expresada formalmente para esta nueva situación como:

al ser E (mim'i) = 0 ( i ≠ i' ) se tiene que:
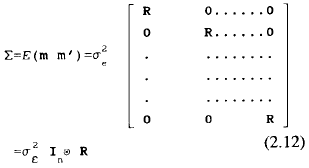
Satisface la siguiente igualdad:
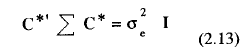
donde
C*' es una matriz de orden (q - 1) x q cuyas filas están formadas por q - 1 vectores de coeficientes ortonormales que definen comparaciones de interés y σe 2 en un escalar mayor que cero que representa el error experimental de los contrastes (Boik, 1981).
Esta situación donde la varianza no depende del intervalo temporal entre observaciones, puesto que todas las posibles diferencias entre dos cualesquiera tratamientos tienen la misma varianza, si bien es menos restrictiva que la situación descrita anteriormente donde se requería simetría combinada, no por ello deja de ser rebuscada a la hora de modelar estructuralmente las respuestas de los sujetos registrados temporalmente, y es, como señalan O'Brien y Kaiser (1985), comúnmente contravenida en este tipo de diseños.
Así pues, satisfacer la condición de simetría se nos antoja irreal y cumplir la condición de circularidad es difícil de lograr bajo muchas condiciones, como ocurre, por ejemplo, con los datos obtenidos en las investigaciones de carácter longitudinal en los campos clínicos, educativos e industriales. Obviamente, en estas situaciones un investigador no debe confiar que sus datos conformen el tipo de matriz estructural esférica requerida por el usual modelo del AVAR con valores esperados mixtos definidos en la ecuaciones (2.1-2.7). Por supuesto, nada más apartado de la realidad, que esperar que las correlaciones entre todos los pares de medidas repetidas sean uniformes. Claramente, como apuntan Kogan et al. (1979) uno esperaría que las observaciones llevadas a cabo en tiempo sucesivos o contigüos estén más altamente correlacionadas que las de los registros que no son adyacentes; es decir, que la correlación entre las puntuaciones decrecerá a medida que incrementemos los intervalos temporales.
Usualmente, para hacer frente al incumplimiento de la asunción de circularidad multimuestral los procedimientos F conservadora y de F ajustada propuestas por Geisser y Greenhouse (1958) y por Greenhouse y Geisser (1959) son utilizados. Sin embargo, el problema con estas pruebas es que son excesivamente conservadoras, pues como señala Jones (1987) ambas fueron desarrolladas para satisfacer bandas seguras más que aproximadas. Alternativamente, Cole y Grizzle (1966) partiendo del hecho que las observaciones obtenidas en los diseños de muestras divididas están correlacionadas y, por tanto, son esencialmente de naturaleza multivariada han sugerido que el método adecuado para analizar tales diseños es el procedimiento multivariado de medidas repetidas. Y, si bien es cierto que el enfoque multivariado permite a la matriz de varianzas-covarianzas tener cualquier estructura a la hora de contratar los efectos principales, interacciones, efectos simple y subefectos, no lo es menos que este procedimiento, además de requerir que el número de sujetos sea mayor que el número de observaciones (pues para hacer inferencias acerca de los parámetros desconocidos β , la matriz Σ, además de arbitraria, debe ser simétrica y definida positiva de orden q), está sobreparametrizado [ya que utiliza los q ( q + l ) / 2 elementos contenidos en la matriz de varianzas-covarianzas], es menos parsimonioso y tiene dificultades a la hora de incorporar observaciones perdidas (Kenward,1987).
Así pues, llegados a este punto, consideramos de capital importancia tener presente algún planteamiento que modele la correlación serial de los datos, de modo que si ésta resulta ser significativa pueda ser removida de las respuestas efectuadas por los sujetos. Si bien en la actualidad existen abundantes modelos a la hora de describir la estructura correlacional de la matriz Σ (ver Box-Jenkins, 1976), nosotros restringiremos nuestro trabajo a situaciones donde los individuos son observados sucesivamente sobre el tiempo un número arbitrario de veces y consideraremos el procedimiento de estimación mínimo cuadrático generalizado (MCG) con la estructura del error modelada a través de procesos autorregresivos y de medidas móviles (ARMA) relativamente simples AR(1) y MA(1). Este enfoque se puede generalizar a una amplia variedad de modelos a la hora de especificar la dependencia serial de la matriz de varianzascovarianzas entre las medidas repetidas y depende de un reducido número de parámetros; por lo general no más de cuatro, si bien lo más frecuente es que Σ sea una función de σ2 ε, σ2 π y ø 1 [el componente de la varianza asociado con la kth medida del ith sujeto, el componente de la varianza vinculado con el factor aleatorio sujetos y el coeficiente del modelo de dependencia serial AR(1) implicado]. La correspondiente matriz de varianzas-covarianzas para esta cuarta y última situación adopta la forma que sigue para el vector respuesta del ith sujeto.

donde
σ 2V ( 1 - ø1)-1 = σ2 ε (ver nota 1 para una demostración) y ø1 es el parámetro autorregresivo de orden uno.
Puesto que E (mi m'i’) = 0 (i ≠ i) se tiene que
NOTA 1. Aunque el componente del error filtrado σ2v no lo conocemos si puede ser obtenido indirectamente a partir de la varianza de εq para el modelo autorregresivo de primer orden, como puede apreciarse de la demostración que sigue dado que según el supuesto de estacionariedad la varianza de εq es la misma para todo q
σ 2ε = E(ε2q) = E( ø1 εq-1 + vq)2
=ø12 E(ε2q-1 ) + E(vq2) 2ø1 E( εq-1 vq)
σ2ε - ø2 σ2ε = σ2v
σ2ε ( 1 - ø2 ) = σ2ε = σ2v ( 1 - ø2 )-1
Finalmente, para terminar este apartado no queremos dejar sin referir dos aspectos. Por un lado, la idea de incorporar la correlación serial dentro del modelo no es original, pues bien de una forma u de otra, ha estado presente con anterioridad en los ya clásicos trabajos de Box (1954), Humphereys (1960) y Danford y otros (1960); sin embargo, hasta fechas recientes no se ha efectuado un modelamiento explícito de la estructura correlacional de la matriz Σ, tal y como ponen de manifiesto los trabajo de Jones (1987), Diggle (1989), Pantulla y Pollock (1985), Rochom y Helms (1989) y Andersen y otros (1981). Por otro lado, al modelar la estructura del error este enfoque constituye un ajuste razonable entre la situación en exceso restrictiva donde se asume que la matriz Σ tiene una estructura correlacional que cumple con la condición de simetría combinada y la situación en exceso liberal donde se permite a la matriz de varianzas-covarianzas tener cualquier estructura (procedimiento multivariado de medidas repetidas).
3. El problema de la correlación serial
Cuando la dependencia serial está presente surgen dificultades a la hora de interpretar los análisis alcanzados con el modelo mixto del AVAR tal y como ha sido definido en las ecuaciones del apartado anterior que van del 2.1 al 2.6, pues al utilizar este modelo uno debe asumir que los errores (la diferencia entre el valor observado y el valor predicho en el modelo de diseño experimental o en la ecuación de regresión) asociados con cada puntuación son independientes. Sin embargo, el cumplimiento de esta asunción, que como dijimos con anterioridad implica correlación constante o que C* ‘ Σ C* fuese una matriz diagonal, es difícil de lograr en los diseños de medidas repetidas con las observaciones ordenadas sobre el tiempo. Usualmente, en los diseños de series de tiempo interrumpidas con presencia de correlación serial, se puede observar cómo los errores que exceden a su valor predicho son adyacentes y cómo los que son menores que su valor predicho también lo son. Pues bien, un fenómeno similar acontece en los diseños de medidas repetidas con muestras divididas, de tal forma que si la kth respuesta del ith sujeto está por encima o por debajo de su propia media hay una tendencia con probabilidad que excede a 0.50 de que la k'th respuesta siguiente también esté por encima o por debajo de su propia media ( εik ≥ 0, εik+1≥ 0 y εik ≤ 0, εik+1 ≤ 0) esta formalización describe una correlación serial positiva, la cual es la más frecuente observada en las Ciencias Sociales y Comportamentales (Maddala, 1977). Surge correlación serial negativa, cuando la ocurrencia de la kth respuesta que se encuentra por encima de la propia media del ith sujeto, incrementa la probabilidad superior a 0.5 de que la siguiente k'th respuesta se ubique por debajo de su propia media ( εik ≥ 0, εik+1 ≤ 0 y εik ≤ 0, εik+1 ≥ 0 ) y a la inversa.
Este es el usual patrón que presentan las respuestas de los sujetos cuando se registran ordenadamente sobre el tiempo por falta de aleatorización, o bien porque éste constituya la variable de interés. Cuando esto suceda, las inferencias causales que realizamos con el habitual modelo del AVAR de medidas repetidas deberán ser cuestionados. Pues, si bien es cierto que los parámetros estimados de los efectos principales e interacciones están insesgados, no lo es menos, como puede observarse en las tablas 5.2. y 5.3, que su eficiencia está puesta en entredicho, ya que los correspondientes errores estándar están estimados incorrectamente. (Ver Vallejo 1989, pp. 145-147).
Desafortunadamente, la falta de independencia entre las puntuaciones de los sujetos constituye una afección que contamina los datos registrados temporalmente, pues las respuestas actuales del ith sujeto están mediatizadas por las respuestas acaecidas en un tiempo anterior. El modo en que lo ocurrido en el pasado influye en lo que acontece en el presente dependerá del valor que tome la memoria que internamente opera en las respuestas de los sujetos. La forma e intensidad de esta remembranza puede obtenerse mediante el cálculo de las funciones de autocorrelación-autocorrelación parcial y a través del examen resultante de contrastar el correlograma empírico con el teórico.
Por lo general, la predicción a la que nos hemos referido más arriba, se puede concretar un poco más diciendo que la observación yik es pronosticada en alguna proporción desde las medidas pasadas yik-1, yik-2,..., yik-q o desde algún componente aleatorio del error vik-1, vik-2.... , vik-q que forma parte del sistema. Estos dos tipos de dependencia, junto con su combinación y el grado de memoria, delimitan la mayor parte de los modelos de correlación serial, algunos de los cuales son expuestos en la tabla 3.1.
De estos modelos el más simple a la vez que se ha manifestado el más frecuente en las Ciencias Sociales es el autorregresivo de orden uno (Theil, 1971; Simonton, 1977). Bajo este proceso, se asume que el error es una función de un error previo, tal y como puede apreciarse en el diagrama de la figura 3.1, y que el coeficiente autorregresivo ø1 se encuentra comprendido entre -1 y +1 si bien la situación más frecuente es 0 ≤ ø1 ≤ 1. Ver Tabla 3-1.
4. Un modelo para las medidas repetidas incorporando la dependencia serial
Considérese un sistema de M ecuaciones de regresión en el cual una sola observación es efectuada para cada una de las n unidades experimentales en cada uno de los q igualmente espaciados periodos de tiempo, bajo la acción de p variables explicativas. La típica ecuación para el ith sujeto es
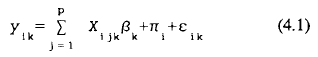
donde Xijk representa el valor del jth tratamiento para la ith unidad experimental en el tiempo q, βk denota un conjunto de parámetros desconocidos que deben estimarse desde los datos, πi es el efecto del sujeto aleatorio y εik es el efecto asociado con la kth medida para el ith sujeto muestral. Ver Figura 3-1.
Es asumido que los errores aleatorios π1; son independientes
π1 - N ( 0, σ2π ) (4.2)
Y que los εik tienen una estructura AR(1)
εik = ø1 εi k-1 + vik (4.3)
donde los vik se distribuyen normal e independientemente con varianza σ2V, εik es independiente de εi’k y εi1 se distribuye de manera similar a ε ik; de modo que εik definido en (4.3) es estacionario. En el caso de que las varianzas se incrementasen con k deberíamos de incorporar la tendencia, o bien integrar los datos.
La forma vectorial del modelo para eI Iith sujeto es
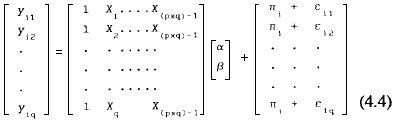
si ponemos en forma compacta los datos para todos los sujetos el modelo completo se escribiría como
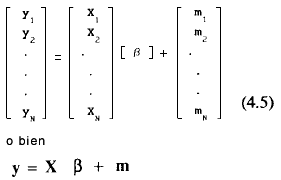
donde y es un vector de observaciones de orden (Nq x 1), X es una matriz de constantes de orden (Nq x pq), β es un vector de parámetros del modelo de orden (pq x 1) y m es un vector de errores aleatorios asociados con el vector de puntuaciones y de orden (Nq x 1).
Para hacer más operativo el modelo debemos de hacer algunos supuestos en relación con m. Un conjunto de asunciones simples es
E (mi) = 0
E (mi m’i,) = 0
E ( mi m’i) = Σ i
E ( m m’) = Σ (4.6)
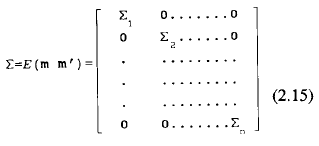
donde Σ, como vimos en la ecuación (2.15), es una matriz diagonal formada por bloques cuyas entradas distintas de cero están compuestas por N submatrices de orden (qi x qi). Estas submatrices dependen de los componentes de varianza σ2v y σ2π y del parámetro o parámetros subyacentes al modelo de dependencia serial, en nuestro caso, la matriz de covarianza subyacente a los datos del ejemplo simulado en el apartado 5, depende de σ2v , σ2π y ø1.
Además, también se asume que y = (y1,...,y' N), siendo y¡ = (yij1,..., yijk), tiene una distribución normal multivariada, aspecto éste que a veces tan sólo ocurre tras filtrar los datos, y su distribución es dada por
y ~ ( μ , Σ ) (4.7)
donde Σ ya ha sido definida anteriormente y μ es
μ = E (y) = E(X β + m) = X β + E (m) = Xβ (4.8)
Establecidas las asunciones sobre el modo en que se alcanzan las observaciones en el modelo de la ecuación (4.5), debemos pasar a obtener el vector de coeficientes β. Para ello es bien conocido que el estimador MCG o de Aitken puede ser utilizado.
β = [ X' Σ( ø1)-1 X]-1 X' Σ (ø1)-1 y (4.9)
y la matriz de varianzas asociadas es
Var. (β) = [ X ‘ Σ (ø 1)-1 X ]-1 (4.10)
Asumiendo que el parámetro autorregresivo (ø1) y los componentes de la varianza (σ2v y σ2π) son conocidos, el estimador MCG obteniendo al utilizar la matriz de varianzas-covarianzas (Σ = σ2πΩ + σ2v ) J , además de ser una función lineal de y, coincide en promedio con el verdadero valor del parámetro [E(β~)=β] y posee menor varianza que cualquier otro estimador lineal insesgado (Parks, 1967).
Cuando el valor de los parámetros σ 2v σ2π y ø 1 es desconocido, como ocurre generalmente en la práctica totalidad de las ocasiones, y no disponemos de algún procedimiento de estimación no lineal que obtenga simultáneamente los estimadores para σ2v σ2π y ø1 debemos proceder a su estimación por etapas sucesivas, pues un aproximado análisis requiere estimar Σ-1 o la apropiada matriz de transformación P. Para este cometido las técnicas de estimación disponibles son múltiples. Por lo que a la estimación de los componentes de la varianza se refiere, actualmente no hay resultados definidos a la hora de decidir cual de ellas es la mejor cuando los diseños no están balanceados; sin embargo, cuando los distintos grupos de nj están equilibrados y/o las observaciones no se han extraviado, Swallow y Searle (1978) nos dicen que los diferentes métodos producen sustancialmente los mismos resultados. En cuanto a la estimación del parámetro autorregresivo, lo acertado y cómodo, es utilizar algún procedimiento de estimación máximo verosímil, más aún en el caso de disponer de puntos de observación restringidos. Para ello se requiere encontrar el estimador de ø1 que minimice alguna función en la que se encuentren incorporados los errores. Como es lógico, este procedimiento necesita incorporar algún programa de cálculo que busque para el mínimo de forma sistemática, pues como dijimos en el apartado 3 el parámetro ø1 admite un amplio número de estados. Seguidamente apoyándonos en las investigaciones de Hasza (1980), Jones (1987) y Pantulla y Pollock (1985) vamos a presentar aproximaciones a los estimadores máximo verosímiles (EMV) de ø1 , σ2v y σ2π.
Asumiendo que q1 ≥ 2 una aproximación al EMV de ø1 que bajo ciertas condiciones de regularidad se ha mostrado consistente puede obtenerse como
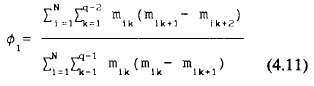
Conociendo ø1 una aproximación insesgada al de σ2v nos es dada por la expresión
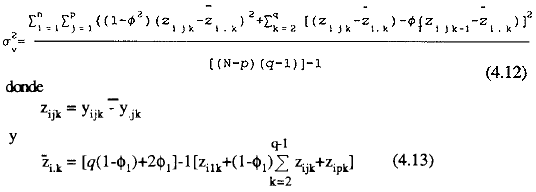
Finalmente, una aproximación insesgada al EMV de σ2π puede ser obtenida desde σ2v+ qσ 2πcomo
![]()
Obtener el estimador MCG dado en la ecuación (4.9) puede ser bastante trabajoso computacionalmente, dado que Σ es una matriz de orden (Ng x Nq). Sin embargo, si una matriz de transformación P puede ser descubierta, de modo que la matriz de varianzas-covarianzas obtenida desde los residuales filtrados tenga simetría combinada, el procedimiento se simplifica enormemente; pues el estimador β puede ser alcanzado al aplicar el procedimiento de los mínimos cuadrados ordinarios a la matriz y vector de variables X e y transformados por P.
Varios procedimientos existen para la construcción de la matriz de transformación. Una forma relativamente sencilla de obtener P es haciendo uso del teorema de descomposición de Cholesky. En este teorema se nos dice que si una matriz D es definida positiva, existe una matriz P, no singular, tal que P' P = D. Así pues, en el caso que nos ocupa, podemos encontrar una matriz P' que multiplicada por P sea igual a Σ-1 y que cumpla con las relaciones
P’P = Σ-1
P Σ P’=I (4.15)
donde P' es una matriz triangular con los elementos por debajo de la diagonal distintos de cero.
Por lo tanto, premultiplicando al modelo de la ecuación (4.5) por P se obtiene.
Py = PXβ + Pm (4.16)
haciendo
y~ = PY
X~ = PX
m~ = Pm
Los errores transformados están ahora incorrelacionados y el estimador β~ que cumple las propiedades del teorema Gauss-Markov es
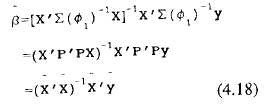
A partir de aquí, la suma de cuadrados para la hipótesis (SCH) y para el error (SCE) son respectivamente,
SCH = Y’Y (X’X)-1 X’Y
SCE= Y’Y - Y’X (X’X)-1 X’Y (4.19)
Igualmente, según Graybill (1976) la suma de cuadrados H puede ser obtenida usando el teorema de Cholesky en la matriz aumentada
[ X'X : X'Y ] (4.20)
definiendo
X’X = T’T (4.21)
y reemplazando en (4.20) X~' X~ por ( T' )-1 tenemos
t = ( T' )-1X Y (4.22)
de forma que la suma de cuadrados H y la suma de cuadrados E son dadas
SCH = t ' t
SCE = Y’Y - t ‘ t (4.23)
Otro procedimiento alternativo para filtrar el vector de residuales de la ecuación (4.5) y convertirle de este modo en un vector de variables aleatorias incorrelacionadas con varianza σ2v , es acudir a la matriz de transformación P = σ2v Σ-1/2 recomendada por Fuller y Battese (1973). Usando este método, al igual que ocurría con el de la factorización Cholesky descrito anteriormente, la matriz de varianzas-covarianzas subyacente a los datos transformados cumple con el requisito de uniformidad referido en el apartado segundo de este trabajo.
La vía para construir la matriz Σ-1/2 es relativamente sencilla, pues se basa en encontrar las raices y coeficientes de la siguiente auto-estructura
(Σ - λ I )a = 0 (4.24)
donde λ , es una raíz característica asociada con Σ que satisfaga la ecuación polinomial o determinamental siguiente
¦ Σ - λ I ¦ = 0 (4.25)
Así pues, una raíz característica o autovalor de Σ es cualquier λ , tal que Σ - λ I sea singular. Una vez calculados los autovalores, el problema de obtener los autovectores o coeficientes se reduce a resolver un sistema de ecuaciones homogéneas de la forma
Σa - λ a = 0 (4.26)
Para cada autovalor de la matriz Σ existe un autovector a que satisface la ecuación anterior. Así pues, si Σi es una matriz cuadrada de orden q con distintas raíces y a es un vector distinto de cero tal que Σi a = λ a, entonces podemos decir que a es un autovector de Σi asociado con el autovalor λ.
Una vez hallados los autovalores λ 1, λ 2, ..., λ q de Σi y los a1, a2,..., aq autovectores normalizados, tenemos que la descomposición espectral de Σi es
Σi = λ1 a1 a’1 + λ2 a2 a’2 +..
. + λq aq a’q = Σqk=1 λk ak a’k = A Λ A' (4.27)
donde AA' = A'A = I y Λ es una matriz diagonal, por lo tanto,
Σ-1i= A Λ-1 A’ = Σqk-1 λ-1 k ak a' k (4.28)
y la matriz raíz cuadrada de Σ es
Σi1/2 = A Λ1/2 A’ = Σqk=1 λ 1/2 ak a’k (4.29)
donde una de sus propiedades es precisamente (Johnson y Wichern, 1989, sección 2.4).
Σ-1/2i = A Λ-1/2 A = Σqk=1 λ -1/2 ak a’k (4.30)
Esta matriz satisface la relación Σ-1/2 Σ Σ-1/2 = INq la cual como puede apreciarse produce errores incorrelacionados con varianza igual a la unidad. De aquí que al utilizar la transformación P = σ2v Σ-1/2 los errores sean independientes y con varianza igual a σ2v. Así, premultiplicado el modelo de la ecuación (4.5) por la matriz diagonal de bloques representada a continuación
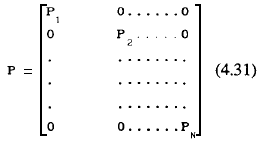
obtenemos el modelo transformado que es expresado algebraicamente en la ecuación (4.16).
5. Ejemplo numérico simulado
Supongamos que un psicólogo clínico desea poner a prueba la eficacia de un tratamiento conductual en la pérdida de peso de ocho pacientes obesos. Para ello los sujetos son divididos aleatoriamente en dos grupos de cuatro, las condiciones de la variable tratamiento (presencia versus ausencia) también son enviados aleatoriamente a los grupos y efectuados registros durante un mes a razón de uno por semana. En la Tabla 5.1. son mostrados los datos del diseño factorial mixto 2 (niveles correspondiente al grupo de tratamiento y de control) x 4 (registros ordenados a través del tiempo) conteniendo vectores de cuatro observaciones por grupo de tratamiento. Los ocho vectores de observaciones pseudo-aleatorios y'ij = [ Yij1, Yij2,..., Yijh] con vector de parámetros μ’j[= μj1, μj2 ,...,μjk] (estos vectores fueron elegidos de manera que los datos describiesen un modelo aditivo, esto es α βjk = 0 y matriz de varianzas-covarianzas Σ (partimos de la hipótesis que C *' Σ1 C * = C*’Σ2C*) fueron obtenidos desde una distribución normal multivariada. Los vectores de observaciones Yij donde Yij~ N (μ, Σ.) fueron logrados transformando el vector de variadas normales estándar zij mediante la ecuación Yij = Tzij + μ0 donde T es la factorización Cholesky de Σ. Los vectores de variadas normales estándar zij fueron logrados por el método de Teichroew descrito por Knuth (1969), los cuales a su vez fueron conseguidos desde variables uniformemente distribuidas generadas por el método congruencial multiplicativo especificado por Naylor y otros (1966), haciendo uso de la rutina GGNML del programa IMSL. Tanto la precisión del procedimiento de normalización por el método de Teichrorew (bandas de error aproximados de 0.0002), como el ajuste de la matriz de varianzas-covarianzas de la muestra a la de la población usando la prueba de chi-cuadrado (Anderson, 1958: pp. 264-267) fueron completamente satisfactorios, no sólo en este caso, sino en un contexto más amplio donde se hace uso de12.000 muestras de 128 puntuaciones cada una. Ver Tabla 5-1.
Una forma adecuada de describir la kth observación del ith sujeto en el nivel de tratamiento j de la tabla (5.1), asumiendo dependencia serial puede ser mediante el modelo de la regresión de codificación de efectos siguiente:
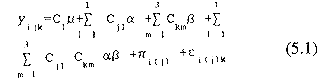
donde para los datos presentados en la tabla 5.1 el vector de puntuaciones (y) y la matriz de diseño (X) para los términos C1μ, (media), Σ11=1 Cjlα (variable entre grupo), Σ3 m=1 Ckmα (variable intra grupos) y Σ11=1 Σ3m=1 Cjl Ckm α β (interacción de ambas variables) toman respectivamente para el caso que nos ocupa la forma que sigue a continuación
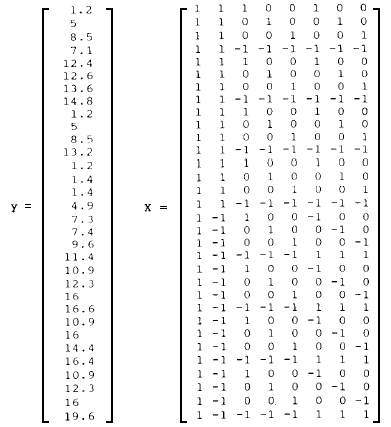
Como fue expresado anteriormente se asume que πi ( j ) ~ NID (0, επ2) y εi( j )k = ø1 εi ( j )k-1+ Vi( j )k, con ø1 < 1 y Vi( j )k ~ NID (0,σ2v).
Antes de pasar a presentar los resultados obtenidos queremos dejar bien sentadas tres cuestiones. En primer lugar, que dado que hemos simulado datos que describen un modelo aditivo, lo correcto sería eliminar el efecto de la interacción de la ecuación (5.1) y dotar al error de un mayor número de grados de libertad, con lo que nuestro análisis sería más poderoso, el que no hagamos ésto se debe a que nuestro propósito persigue solamente fines ilustrativos. En segundo lugar, que la anterior matriz de contrastes (X) y vector de puntuaciones (y) son las del usual modelo del AVAR con ø1 = 0. Como es obvio, en el caso que nos ocupa, el parámetro autorregresivo es distinto de cero, en concreto nosotros hemos simulado los datos dando un valor a ø1 de 0.8; en consecuencia, los valores correspondientes a la matriz X y el vector y deben ser promediados por la matriz de transformación P definida en el apartado 3. La única razón para no hacer ésto obedece a nuestro deseo de hacer los elementos de X y de y lo más sencillo que nos sea posible. Por último, apuntar que una forma de proceder similar deberíamos haber seguido si hubiésemos generado datos modelados por algún otro proceso de dependencia serial. Así por ejemplo, si los datos en vez de seguir un modelo AR(1), hubiesen seguido un MA(1) la matriz Σ en vez de tener la forma descrita en el apartado 4 tomaría esta nueva disposición:
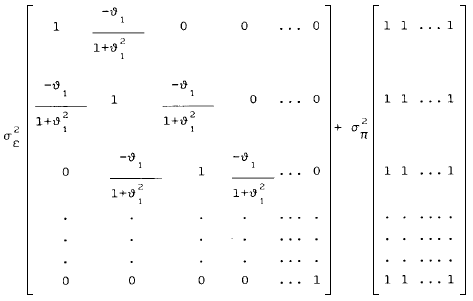
Finalmente, en la Tabla 5.2 presentamos un cuadro resumen del análisis de la varianza bajo el supuesto de independencia serial y bajo la presencia de correlación modelada por ø1 = 0,8. En esta tabla queda claramente puesto de manifiesto cómo la falta de independencia de los errores incrementa falsamente la significación del efecto de la variable intra alrededor de un 45%. Por otra parte, en la tabla 5.3. se puede comprobar, cómo la autocorrelación no afecta al valor de los parámetros estimados bajo el modelo usual del AVAR; sin embargo, si bien es cierto que los estimadores no están sesgados, no lo es menos que estos son menos eficientes que los obtenidos mediante el modelo del AVAR que contempla la correlación existente.
6. A modo de conclusión
En el presente trabajo hemos argumentado en contra de proceder con el usual modelo mixto del AVAR cuando la asunción de independencia de los errores asociados con los registros efectuados a lo largo del tiempo es incumplida, pues esta violación puede afectar gravemente a la eficiencia de las estimaciones llevadas a cabo, lo cual como es sabido conlleva a que infravaloremos, o como generalmente ocurre, sobrevaloremos los verdaderos valores de los efectos principales y de las interacciones. Para hacer frente a este grave inconveniente, hemos seguido acudiendo al modelo mixto del AVAR, ya que a nuestro modo de ver éste sigue siendo el candidato natural para acometer correctamente este tipo de situaciones, pero con la estructura del error modelada mediante un proceso autorregresivo de orden uno, o bien a través de algún proceso ARMA más complejo. Por último, reseñar que esta manera de proceder, además de poder aplicarse cuando los sujetos son observados un número aleatorio de veces y los grupos de unidades experimentales no se encuentran completamente balanceados, puede extenderse a situaciones teóricamente más complejas, como puede suceder en aquellos casos en los cuales dispongamos de distintos grupos de sujetos formados aleatoriamente en los que efectuemos registros tanto antes como después de la presentación de los tratamientos.
BIBLIOGRAFIA
Andersen, A.H.; Jensen, E.B. y Geart, S. (1981). Two-way analysis of variance with correlated errors. International Statistical Review 49, 153-169.
Anderson, T.W. (1958). An Introduction Multivariate Statistical Analysis. New York: Wiley and Sons, Inc...
Boik, R.J. (1981). A priori test in repeated measures design: Effects of nosphericity. Psychometrika 46, 241-255.
Box, G.E.P. (1950). Problems in the analysis of growth and wear curves. Biometrics 6, 362-387.
Box, G.E.P. (1954). Some theorems on quadratic forms applied in the study of analysis of variance problems II. Effects of inequality of variance and of correlation between errors in the two-way classification. Annals of Mathematical Statistics 25, 484-498.
Box, G.E.P. y Jenkins, G.M. (1954). Time Series Analysis: Forecasting and Control, 2nd Ed. San Francisco: Holden-Day.
Cole, J.W.L. y Grizzle, J.E. (1966). Applications of multivariate analysis of repeated measures experiments. Biometrics, 44, 547-565.
Diggle, P.J. (1988). An approach to the analysis of repeated measurements. Biometrics, 44, 959-971.
Fuller, W.A. y Battese, G.E. (1973). Transformations for estimation of linear models with nested error structure. Journal of the American Statistical Association 68, 626-632.
Geisser, S y Greenhouse, S.W. (1958). An extension of Box's result on the use of the F distribution in multivariate analysis. Annals of Mathematical Statistics 29, 885-891.
Graybill, F.A. (1976). Theory and application of the Linear Model. North Scituate, Massachusetts: Duxbury Press.
Greenhouse, S.W. y Geisser, S. (1959). On methods in the analysis of profile data. Psychometrika 24, 95-102.
Hasza, D.P. (1980). A note on maximun likelihood estimation for the first order autoregresive process. Comunications in Statistics, Series, A, 1511-1515.
Humpheys, L.G. (1960). Investigation of the simplex. Psychometrika 24, 313-323.
Huynh, H. y Feldt, L.S. (1970). Conditions under which mean square ratios in repeated measurements designs have exact Fdistributions. Journal of the American Statistical Association 65, 1582-1585.
Johnson, R.A. y Wichem, D.W. (1989). Applied Multivariate Statiscal Analysis. 2nd Ed. New Jersey: Prentice-Hall.
Jones, R.H. (1987). Serial Correlation in unbalanced mixed models. Bulletin of the International Statistical Institute, 46,105-122.
Kenward, M.G. (1987). A method for comparing profiles of repeated measurements. Applied Statistics 36, 296-308.
Knuth, D.E. (1969). Seminumerical Algorithms: The Art of Computer Prograamimg. Massachusetts: Addison-Wesley.
Kogan, C.J.; Keselman, H.J. y Mendoza, J.L. (1979). Analysis of repeated measurements. British Journal of Mathematical and Statistical Psychology 32, 269-286.
Maddala, G.S. (1977). Econometrics. New York: McGraw-Hill. (Traducido de la edición en inglés por la propia editorial).
Naylor, H.T.; Balintfy, J.L.; Burdick, D.S. y Chu, K. (1966). Computer Simulation Techniques. New York: John Wiley.
O'Brien, K.G. y Kaiser, M.K. (1985). MANOVA method for analyzing repeated measures designs: An extensive primer. Psychological Bulletin 97, 316-333.
Pantulla, S.G. y Pollock, K.H. (1985). Nested analysis of variante with autocorrelated errors. Biometrics 41, 909-920.
Parks, R.W. (1967). Efficient estimation of a system of regression equations when disturbances are both serially and contemporaneously correlated. Journal of the American Statistical Association 62, 500-510.
Rochon, J. y Helms, R.W. (1989). Maximun Likelihood estimation for incomplete repeated measures experiments under on ARIMA covariance structure. Biometrics 45, 207-218.
Rouanet, H y Lépine, D. (1970). Comparison between treatments in a repeated measurements design: ANOVA and multivariate methods. British Journal of Mathematical and Statistical Psychology 23, 147-163.
Scheffé, H. (1959). The Analysis of Variance. New York: John Wiley.
Simonton, D.K. (1977). Cross-sectional time-series experiments: Some suggested statistical analysis. Psychological Bulletin, 84, 489-502.
Swallow, W.H. y Searle, S.R. (1978). Minimun variance quadratic unbiased estimation (MINVQUE) of variance components. Technometrics 20, 265-272.
Theil, H. (1971). Principles of Econometrics. New York: John Wiley.
Vallejo, G. (1986). Aplicación del análisis de series temporales en diseños con N=1: Consideraciones generales. Revista Española de Terapia del Comportamiento 4, 1-29.
Vallejo, G. (1989). Regresión de series de tiempo con mediciones igualmente espaciados. Anuario de Psicología 43, 126-155.
Winer, B.J. (1971). Statistical Principles in Experimental Design. 2nd Ed. New York: McGraw-Hill.