Psicothema was founded in Asturias (northern Spain) in 1989, and is published jointly by the Psychology Faculty of the University of Oviedo and the Psychological Association of the Principality of Asturias (Colegio Oficial de Psicología del Principado de Asturias).
We currently publish four issues per year, which accounts for some 100 articles annually. We admit work from both the basic and applied research fields, and from all areas of Psychology, all manuscripts being anonymously reviewed prior to publication.
Psicothema, 2002. Vol. Vol. 14 (nº 1). 174-180
Juan Botella
Universidad Autónoma de Madrid
Cuando se emplea un diseño de investigación que se completará con un contraste sobre la diferencia de medias para muestras relacionadas se produce a veces la pérdida de algunos de los valores. La forma de actuar más popular en esas situaciones consiste en suprimir los sujetos u observaciones incompletos. En el presente artículo se analizan las consecuencias de la supresión, se revisan otras formas de actuar y se realiza un estudio de simulación de las consecuencias que esos métodos alternativos tienen sobre las probabilidades de cometer errores tipo I y tipo II. Se concluye proponiendo algunas recomendaciones prácticas para afrontar estas situaciones.
Power of alternative tests for two paired samples with missing data. When a research design that will use a test of means difference for matched samples is to be applied sometimes part of the observations on either of the variables are missing. The usual way to face those situations is the supression of the incomplete subjects or observations. In the present paper the consequences of the supression are analyzed, other alternatives are reviewed and a simulation study is reported. In the simulation the consequences of those alternatives over the probabilities of Type I and Type II errors are studied. Some practical recommendations for these situations are also included.
Un problema frecuente en la práctica del análisis estadístico es la carencia de parte de los datos (missing data; Anderson, Basilevsky y Hum, 1983; Little y Rubin, 1987; Redman, 1992; Schafer, 1997). El presente trabajo se centra en el caso en que se observan dos variables normales correlacionadas, X1 y X2, e interesa contrastar la hipótesis de no diferencia entre las medias poblacionales (H0: μ1 - μ2 = 0).
El esquema general de la situación es el siguiente:
X11, X12, ...,X1n X1n+1, X1n+2, ..., X1n+n1
X21, X22, ..., X2n X2n+1, X2n+2, ..., X2n+n2
Disponemos de n pares de observaciones completas, más n1 observaciones en las que falta el valor de la variable X2 y más n2 observaciones en las que falta el valor de la variable X1 (obsérvese que según esta nomenclatura los valores X1n+1 y X2n+1 no se refieren a dos variables del mismo sujeto o unidad de análisis). Por razones de claridad expositiva vamos a restringirnos por ahora a aquellos casos en los que la pérdida de datos se produce solo en una variable (n2=0).
Una forma frecuente de actuar en esta situación es la supresión, o simple eliminación para el análisis de las unidades (sujetos, observaciones) de los que faltan datos, aplicando las técnicas estadísticas usuales a las unidades que están completas (procedimiento pairwise en SPSS). Dado que la supresión implica desperdiciar la información contenida en la variable que sí se ha observado, merece la pena estudiar otras alternativas que aprovechan esa información. En las secciones siguientes se analizan las consecuencias de la mera supresión, se exponen otras alternativas de actuación y se estudian, mediante el método Monte Carlo, las consecuencias que esas alternativas tienen en términos de las probabilidades de cometer errores tipo I y II. Pero antes de continuar conviene dedicar unas líneas a otro supuesto que se suele asumir en estas situaciones: el de la aleatoriedad del mecanismo que produce la pérdida de datos.
Cuando se opta por la supresión se asume el supuesto implícito de la aleatoriedad del mecanismo de censura, supuesto que no se suele contrastar. Este supuesto establece que el conjunto de observaciones completas es una submuestra completamente aleatoria de la muestra que se intentó observar. A veces las pérdidas se producen por simples fallos en los sistemas de recogida de información, seguramente aleatorios, pero en otras ocasiones los mecanismos que las producen son más complejos. La principal distinción hay que establecerla entre pérdidas aleatorias y pérdidas no aleatorias. La violación de este supuesto podría tener consecuencias imprevisibles sobre las conclusiones y, en cualquier caso, imposibilitaría la aplicación de las otras opciones que trataremos a continuación. Cook y Campbell (1979) consideran a la violación de este supuesto como una de las principales amenazas a la validez interna de una investigación.
En consecuencia, un primer paso en estas situaciones debe ser el análisis del propio mecanismo de pérdida, para comprobar si es razonable mantener la hipótesis de que la pérdida se produce al azar. Con la información disponible se puede estudiar la hipótesis de que la pérdida está asociada a los valores de la variable observada, pero no la de que está asociada a los valores de la propia variable en la que faltan datos. Es decir, la propia pérdida de información puede convertirse en una variable dicotómica interesante de analizar, aunque sólo sea como paso previo para poder asumir que nos encontramos en el caso de pérdida aleatoria y así proceder a utilizar las técnicas que describiremos en la sección siguiente, pues todas ellas asumen este supuesto. En la terminología antes expuesta, estudiaríamos si los valores en X1 de las n observaciones completas difieren de las n1 observaciones en esa variable en las que falta X2.
Inconvenientes de la supresión pura
La supresión, que como ya hemos dicho consiste en restringir el análisis a la submuestra de n pares de observaciones completas, tiene algunos inconvenientes. En primer lugar, supone un evidente recorte en la potencia del contraste con respecto a la potencia pretendida al fijar el tamaño de la muestra original. Si no se rechaza la hipótesis nula puede quedar la duda de cuál hubiera sido la conclusión en caso de haber contado con la potencia asociada al tamaño de la muestra originalmente intentada (Graham, Hofe y Piccinin, 1994; Orme y Reis, 1991).
Un segundo inconveniente de la supresión es que supone actuar en la dirección opuesta a la que debe ser una de las guías principales del analista de datos: utilizar toda la información disponible y de la forma más eficaz. Desperdiciar las observaciones desemparejadas es incompatible con esta guía. Mas bien parece que habría que intentar aprovechar la información contenida en los datos incompletos. Veámoslo con algo más de detalle. En el contraste de diferencia de medias de dos variables normales con muestras relacionadas se utiliza el estadístico (e.g., Pardo y San Martín, 1998),
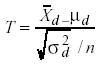 (1)
(1)
cuya distribución es N(0, 1) y μd=0 para la hipótesis de no diferencia, donde
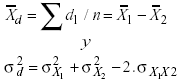 (2)
(2)
Habitualmente la varianza de las diferencias directas (σd2) es desconocida, por lo que suele estimarse a partir de la varianza de diferencias muestrales, que es la que se sustituye en el denominador de la fórmula (1). En tal caso el estadístico T no se distribuye N(0, 1) sino t de student con n-1 grados de libertad.
Las dos medias poblacionales (o la diferencia entre las medias poblacionales) se estiman a partir de las medias de cada muestra de observaciones; su estimación no se ve afectada por la correlación entre las variables. En consecuencia, sería correcto utilizar las n+n1 observaciones de X1 para estimar m1 y las n observaciones de X2 para estimar μ2. Pero no solo sería correcto, sino que la estimación de μ1 se beneficiaría del incremento de eficiencia que acompaña al aumento del tamaño de la muestra utilizada para estimar el parámetro. Por el contrario, el estimador de σX1X2 se basa en parejas de valores y por tanto, la simple eliminación de las unidades incompletas no despreciaría información útil para su estimación.
Alternativas a la supresión pura
Hay otras opciones alternativas a la supresión, como la imputación, la reconversión y el uso de estadísticos específicos. Dado que el principal inconveniente de la supresión es que implica una pérdida de potencia con respecto a la que se hubiera obtenido con una muestra del tamaño prefijado, vamos a estudiar las posibles ventajas de estas alternativas en términos de potencia.
La imputación consiste en sustituir los valores perdidos con otros valores estimados a partir de la información disponible; a continuación se aplican las técnicas estadísticas usuales sobre el conjunto total de puntuaciones, parte de ellas observadas y parte estimadas. Hay varios métodos de estimación de estos valores, de los que los más sencillos son la imputación de la media y la imputación por regresión lineal. En el primer caso cada valor perdido se sustituye por el promedio de los valores observados en esa variable (los n valores de X1). Con este procedimiento las medias muestrales no se ven alteradas, pero sí las varianzas puesto que se añaden valores que coinciden con la puntuación central; la varianza muestral resultante será una infraestimación de la varianza poblacional. Concretamente, si designamos por Sn2 a la varianza muestral hallada sobre los valores en X2 de los n pares de observaciones completas y SN2 a la obtenida sobre los n+n1 valores tras imputar la media a los valores perdidos, tendremos que
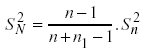
y por tanto es una infraestimación de la varianza poblacional con factor (n-1)/(n+n1 - 1).
Por otra parte, es la varianza muestral de las diferencias la que aparece en la estimación de σd2, y su cálculo no es independiente de la correlación entre las puntuaciones. La imputación por media produce una disminución de la correlación muestral, puesto que en los n1 pares en los que el valor de X2 ha sido estimado la correlación es nula; por tanto, la correlación en los n+n1 pares será menor que en los n pares de observaciones genuinas.
Otra forma de suplir los datos perdidos consiste en la imputación por regresión, en la cual se estiman mediante la ecuación de regresión lineal de X2 sobre X1 (e.g., Botella, León, San Martín y Barriopedro, 2001). Como consecuencia de ello, la varianza de las n+n1 puntuaciones en X2 es también menor que la varianza basada en los n valores de X2, aunque no tanto como cuando se imputa la media. En concreto, la varianza de los pronósticos es igual a la varianza de las n puntuaciones en X2 multiplicado por r2. La varianza de las n+n1 observaciones será sistemáticamente menor que la de las n observaciones auténticas de X2. Por otra parte, también en este caso S2d se ve indirectamente influida por la correlación entre las variables, aunque en un sentido inverso. En concreto, dado que la correlación entre los n1 valores desemparejados de X1 y los n1 valores de X2 estimados es perfecta, la correlación global en los n+n1 pares será mayor que la observada entre los n pares completos. La varianza de las diferencias muestrales (S2d) tenderá a disminuir por ambos factores.
Un método más complejo de estimación es el algoritmo E-M, o de Estimación-Maximización. El primer paso consiste en hacer una estimación (habitualmente por regresión lineal) de los valores perdidos; después se recalculan los parámetros del modelo utilizando tanto las observaciones completas como las completadas mediante la regresión. Con el nuevo modelo se vuelven a estimar los valores perdidos y sobre esos nuevos valores se recalculan otra vez los parámetros. El proceso se repite las veces que sea necesario hasta que se produzca la convergencia; es decir, hasta que la diferencia entre las estimaciones hechas en dos iteraciones consecutivas no sobrepase un criterio arbitrariamente pequeño establecido a priori (Dempster, Laird y Rubin, 1977). Este procedimiento parece especialmente apropiado cuando, a diferencia del caso de la comparación de medias que estamos tratando aquí, se va a realizar un análisis sobre un número grande de variables simultáneamente, en donde la supresión de las unidades con pérdida en alguna de ellas supone un filtro que reduce excesivamente el número de unidades que aún se pueden rescatar para el análisis.
Los métodos de imputación se ven mejorados si al valor estimado se le añade un término de error aleatorio con media cero y varianza igual a la estimada en el análisis de regresión (Kalton y Kasprzyk, 1986). Otras alternativas más recientes recurren al empleo de redes neuronales artificiales (Navarro y Losilla, 2000, 2001). Pero tanto si se imputan los valores utilizando la media, como la regresión lineal, el algoritmo E-M o cualquier otro método, no hay que olvidar que el análisis estadístico no se realiza sólo sobre puntuaciones observadas, sino que algunas de ellas son meras estimaciones. Como Dempster y Rubin (1983) han señalado, existe el peligro de llegar a creer que, después de todo, las puntuaciones han sido recuperadas. Hay que tener presente el hecho de la imputación, el procedimiento utilizado y su magnitud en términos del número de valores estimados, haciéndolo todo ello patente en el informe del análisis.
La reconversión no es más que la transformación de la situación en una de diferencia de medias con muestras independientes. Esta estrategia podría suponer un cierto incremento de potencia con respecto a la supresión sólo si el número de observaciones incompletas es relativamente grande. Así, por ejemplo, si disponemos de 10 pares de observaciones completas y 20 observaciones en las que falta el dato de la variable X2, podría redundar en una mayor potencia desechar la información de los 10 primeros sujetos en la variable X1 y comparar sus valores en X2 con los de los otros sujetos en X1. La razón es que los grados de libertad disponibles si se opta por la supresión son n-1 (9 en este caso), mientras que en caso de aplicar la reconversión serían n+n1-2 (29 en el ejemplo).
El diseño con muestras relacionadas tiene la ventaja de que la varianza de las diferencias es menor cuanto mayor es la correlación entre las variables. En consecuencia, la reconversión podría resultar ventajosa si las variables son linealmente independientes o su correlación es baja, mientras que con correlaciones moderadas o altas probablemente sea indiferente o incluso sea mejor la supresión, al menos en términos de potencia. Se pueden seleccionar aleatoriamente los valores que se retendrán de las variables X1 y/o X2, no tomando en ningún caso ambos valores de un mismo par y tratando de igualar en lo posible los tamaños muestrales. Así, en un caso en el que n=10 y n1=8 se tomarían aleatoriamente 9 de los n pares completos y se retendría su valor en X2, tomando del restante el valor de X1; con este valor más los 8 valores de X1 desemparejados por la pérdida se formarían dos muestras independientes de tamaño 9. Si hay pérdidas en ambas variables los pares completos se dividirían en dos grupos tales que los tamaños resultantes al añadir sus valores a los valores desemparejados fueran lo más igualados posible.
Todo lo dicho hasta aquí sobre la supresión, la imputación y la reconversión puede generalizarse al caso en el que se han perdido datos en ambas variables.
La última alternativa a la que nos vamos a referir es la del uso de estadísticos específicos diseñados especialmente para esta situación. Distinguiremos entre los casos de pérdidas en una o las dos variables. Dentro de cada uno de esos casos el conocimiento total o parcial de la matriz de varianzas y covarianzas ayudaría mucho a determinar el estadístico más apropiado, pero en la práctica esta suele ser completamente desconocida. Por ello hemos seleccionado para nuestro estudio estadísticos que no tienen exigencias con respecto a la correlación; en todo caso algunos de ellos asumen la homocedasticidad de las variables. Dentro del caso de pérdidas en una sola variable Mehta y Gurland (1969a y b) propusieron un método bifásico que exige la normalidad y homocedasticidad. En este método se realiza primero un contraste sobre la independencia lineal, basado en la correlación de Pearson entre los n pares completos. Dependiendo del resultado de este contraste se podría utilizar una técnica expuesta por los autores que exige la aplicación de un complejo procedimiento para la fijación de las constantes que aparecen en la fórmula. Lin (1973) describe varios estadísticos, pero la elección entre ellos dependería del conocimiento parcial de la matriz de varianzas y covarianzas. En concreto, de que la razón entre las varianzas sea conocida, o de que sean linealmente independientes. Nosotros hemos seleccionado el estadístico que propone para el caso de variables homocedásticas, que representaremos por T1. Para los casos en que la matriz de varianzas y covarianzas es completamente desconocida recoge tres soluciones: la simple eliminación, una prueba conservadora en la que la probabilidad de cometer un error tipo I tiene como valor máximo el α nominal y un estadístico basado en la solución de Welch para casos de heterocedasticidad. Hemos seleccionado también para nuestro estudio este último estadístico, al que representaremos por T2. Lin (1973) realiza, además, una simulación tipo Monte Carlo para comparar el comportamiento de algunos de estos estadísticos, aunque es un estudio relativamente limitado. En la misma línea, Morrison (1973) propone un estadístico que exige también la normalidad y homocedasticidad, para el que consigue determinar la distribución exacta siendo la hipótesis nula verdadera.
También se han propuesto varios estadísticos para cuando hay datos perdidos en ambas variables. De entre ellos hemos seleccionado uno de los desarrollados por Lin y Stivers (1974), que no exige la homocedasticidad aunque sí la normalidad; lo representaremos por T3. Por su parte Bhoj (1978) ha presentado un elegante método basado en el resultado de Ghosh (1975). Este último autor demuestra que en ciertas circunstancias una suma de dos variables distribuidas según t de student también se distribuye según t de student. Tomando esta idea como base Bhoj (1978) propone calcular la t estándar para muestras relacionadas sobre los n pares completos y la t para muestras independientes sobre los n1+n2 valores desemparejados, combinando después esos valores en un único estadístico. Propone dos estadísticos distintos según que las variables sean o no homocedásticas. Nosotros representaremos estos estadísticos por T4 y T5, respectivamente. Como en T5 no se asume la homocedasticidad el estadístico aplicado sobre los valores desemparejados no puede ser el estadístico estándar; Bhoj (1978) lo sustituye por la solución dada por Scheffé para casos de heterocedasticidad (las fórmulas de algunos de estos estadísticos específicos se incluyen en el anexo).
Método
En el presente estudio se han incluido las siguientes opciones: supresión (Ts), imputación por media (Tm), imputación por regresión (Trg), reconversión (Trc) y los 5 estadísticos específicos que acabamos de señalar (T1 a T5). El programa fue escrito en BASIC por el autor.
El procedimiento utilizado en la simulación consiste en extraer observaciones de dos distribuciones normales y homocedásticas con un valor de correlación (ρ) prefijado entre ellas, mediante el procedimiento propuesto por Lewis y Orav (1989). Este consiste en generar las variables V y W como independientes N(0,1); si ρ=0 se establece X1=V y X2=W, mientras que si ρ ≠ 0 se establece X1=V y X2 = ρ · V + (1-ρ2)1/2 · W. Los valores de ρ utilizados han sido 0, 0,25 y 0,50. Los valores utilizados para δ han sido 0, 0,50 y 1. Con el primero de ellos se estudió el comportamiento de α para los diferentes valores de correlación, mientras que con los otros dos se estudió la potencia. Cada simulación se realizó con 5000 ensayos.
Se fijaba primero el tamaño original de la muestra (N), sobre la cual se calculaba el estadístico estándar para muestras relacionadas, que representaremos por Tst con objeto de comprobar que el procedimiento daba lugar a buenas estimaciones de la potencia, comparándolos con los ofrecidos por Cohen (1977).
Después se seleccionaban de entre ellos al azar n1 pares, que se trataban como datos perdidos en una de las variables, o n1+n2 pares, que se trataban como n1 datos perdidos en una variable y n2 datos perdidos en la otra. Con estos datos se calculaban los estadísticos incluidos en el estudio y se realizaba el contraste correspondiente, codificando cada ensayo como rechazo o no rechazo. La proporción de rechazos se tomó como una estimación de α o 1-β (dependiendo de que se tratase del caso en el que δ=0 o de alguno de los casos en los que δ>0).
Los valores utilizados para N y para n1, en los casos de pérdidas en una sola variable fueron:
10 (2, 4, 6);
15 (2, 6, 10);
20 (2, 6, 10, 14);
25 (2, 6, 10, 14, 18);
30 (2, 6, 10, 14, 18, 22)
Para estudiar el caso de pérdidas en ambas variables se utilizaron tamaños similares, pero el número de datos perdidos se repartió por igual entre ambas variables. Esto hace un total de 42 combinaciones en cuanto al tamaño de las muestras, el tamaño de la pérdida y su distribución entre las variables. Estas 42 combinaciones se cruzaron con los 3 valores de ρ (0, 0,25 y 0,50) y los 3 valores de δ (0, 0,50 y 1), totalizando 378 simulaciones. En cada una de ellas se obtenía la tasa empírica de rechazos con los valores de α 0,05 y 0,01 en contrastes unilaterales y bilaterales.
Resultados
Vamos a organizar esta sección dividiéndola en tres apartados, relativos a la calidad de la simulación en la generación a priori de tasas de error tipo I y II, a las consecuencias de la supresión pura y a las tasas empíricas en las alternativas seleccionadas.
Tasas a priori de errores tipo I y II
La observación de los resultados con la Tst (antes de la pérdida de datos) nos sirve como validación del procedimiento. En las simulaciones con diferencia de medias igual a cero hemos encontrado proporciones de rechazos muy cercanas al valor del α nominal. En concreto, en contrastes bilaterales con α=0,05 las proporciones de rechazos oscilaron entre 0,0442 y 0,0586, mientras que en contrastes bilaterales con α=0,01 oscilaron entre 0,0078 y 0,0122. En las simulaciones con δ>0 (hipótesis nula falsa), las proporciones de rechazos con Tst sin pérdidas de datos son muy parecidas a los valores de potencia informados por Cohen (1977). En concreto, en la tabla 1 aparecen algunos de los resultados con tamaño del efecto 0,50. Como puede observarse las diferencias son perfectamente asumibles; en consecuencia, podemos aceptar con razonable confianza los resultados obtenidos al eliminar datos.
Consecuencias de la supresión pura
En el caso de α=0,05 las tasas empíricas de rechazo para H0 verdadera oscilan entre 0,0442 y 0,0586; con α=0,01 oscilan entre 0,0072 y 0,0122. En resumen, nunca alcanzan una desviación de 0,01 respecto al valor nominal de α.
Tasas de errores tipo I y II asociadas a las diversas alternativas
Dado que sería demasiado prolijo exponer los resultados de todas las simulaciones, hemos seleccionado en la tabla 2 los de algunas que nos han parecido más representativas. En ellos pueden comprobarse algunos de los efectos que habíamos predicho.
En primer lugar, tal y como era de esperar la reconversión supera en potencia a la supresión cuando el número de datos perdidos es mayor del 50% solo si las variables son linealmente independientes. Cuando la correlación pasa a 0,25 y, sobre todo, a 0,50, el porcentaje de datos perdidos a partir del cual la potencia conseguida con reconversión supera a la conseguida con supresión es muy superior (hasta un 70% de datos perdidos). Los resultados son similares cuando las pérdidas se producen en una de las variables o en las dos. Como sospechábamos, la reconversión no parece una buena alternativa.
En segundo lugar, el sustituir los datos perdidos por sus estimaciones tiene como consecuencia principal un incremento en la probabilidad de cometer un error tipo I, que resulta espectacular en la estimación por regresión. En este último caso se altera sustancialmente la estimación de la matriz de varianzas y covarianzas. Cuando se imputa la media los efectos sobre α y β son sensiblemente menores. Por ejemplo, si se fija un α nominal de 0,01 hemos podido comprobar que las estimaciones de las probabilidades reales tras esa imputación no han excedido nunca 0,05, mientras que la potencia conseguida se incrementa notablemente. Sin embargo, esas potencias no alcanzan los valores que se obtienen cuando se deja el α nominal y se opta por la supresión.
Para que las potencias conseguidas por este procedimiento superen a las obtenidas por supresión hay que mantener α=0,05, sabiendo que la verdadera probabilidad de cometer un error tipo I es algo superior; en las simulaciones que hemos realizado con porcentajes de datos perdidos de hasta el 20%, las estimaciones de esas probabilidades no han sobrepasado nunca 0,09, indicando que ésta podría ser una alternativa razonable en aquellos casos en los que se puede asumir un cierto incremento sobre el α nominal.
En tercer lugar, cuando se producen pérdidas en una sola variable la mejor alternativa si se puede asumir la homocedasticidad es el estadístico T1 de Lin (1973). Esta conclusión es válida para todos los tamaños de pérdida y de correlación estudiados, aunque para el mayor valor de correlación incluido en el estudio la diferencia con respecto a la supresión es pequeña y quizás con valores superiores esa diferencia podría desaparecer o incluso invertirse. Si no se puede asumir la homocedasticidad el estadístico T2 proporciona mejores valores de potencia que la supresión cuando la correlación es 0 ó 0,25, mientras que si es 0,50 esa ventaja se pierde. Cuando se desconoce el valor de la correlación parece más apropiado utilizar T2 en lugar de optar por la supresión.
En cuarto lugar, cuando se tienen datos perdidos en ambas variables la alternativa que proporciona más potencia de entre las estudiadas es el estadístico T3 de Lin y Stivers (1974), mientras que los estadísticos T4 y T5 propuestos por Bhoj (1978) resultan menos apropiados. El hecho de que T3 no exija la homocedasticidad lo hace más recomendable, puesto que puede aplicarse sin siquiera realizar un contraste previo de homocedasticidad.
Discusión
En las situaciones como las que estamos estudiando, la manera de actuar más frecuente es la supresión pura. Esto implica una pérdida de potencia y una renuncia a explotar toda la información disponible. En el estudio de simulación que hemos hecho se han estudiado las consecuencias sobre las probabilidades de cometer errores tipo I y II de diversas alternativas propuestas en la literatura para afrontar estas situaciones.
Sin embargo, nuestros resultados muestran que cuando el número de datos perdidos es pequeño (no superior al 10%), la supresión puede ser una buena opción, sobre todo si la correlación entre las variables se sospecha positiva moderada o alta. Los métodos de imputación simple que hemos estudiado tienen efectos graves sobre α, mayores cuando se estima por regresión y menores cuando se estima por la media. Estos procedimientos no parecen muy apropiados, al menos sin una corrección mediante un término de error. Cuando se han perdido más de un 10% de los datos y en una sola variable se debe hacer un contraste previo de homocedasticidad. Si se mantiene la hipótesis nula el estadístico más apropiado sería T1, mientras que en caso contrario habría que elegir T2. No obstante, hay que tener presente lo dicho anteriormente, puesto que si la correlación se sospecha alta la opción de la supresión puede ser la más ventajosa. Por último, en caso de pérdidas en ambas variables el estadístico más apropiado es T3.
En cualquier caso, hay que resaltar el hecho de que los resultados obtenidos no son por ahora generalizables a todos los casos. Por ejemplo en el contraste al que nos estamos refiriendo muchas veces se ignora el supuesto de normalidad cuando se utilizan muestras moderadamente grandes, puesto que se sabe que en esos casos la violación del supuesto de normalidad apenas afecta a las probabilidades de error tipo I y II. Por el contrario, no conocemos el comportamiento de los estadísticos que hemos estudiado cuando se viola ese supuesto. Por otra parte, en todas las simulaciones realizadas se han utilizado variables homocedásticas, aunque algunos estadísticos no lo exigían. Tampoco conocemos las variaciones que sufriría la potencia con respecto a la supresión si las varianzas fueran marcadamente distintas. Dejamos el estudio de los efectos de estas circunstancias para trabajos futuros.
No queremos terminar esta discusión sin resaltar que en estas situaciones es imprescindible que como primera medida se ponga a prueba de alguna forma el supuesto de aleatoriedad del mecanismo de pérdida, cuya violación supondría una seria amenaza a la validez de la investigación.
Fórmulas de los estadísticos específicos T1, T2 y T3 del texto (T4 y T5 se basan en las fórmulas conocidas de la diferencia de medias para muestras independientes y relacionadas). El esquema es el descrito al comienzo de la introducción.
(a) Estadístico T1, tomado de Lin (1973, pág. 700),
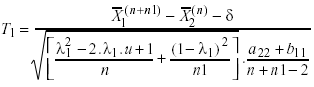
T1 se distribuye aproximadamente tn+n1-3
Donde
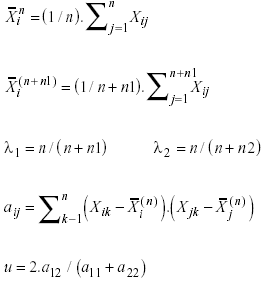
δ = 0 para la hipótesis especificada (1).
(b) Estadístico T2, tomado de Lin (1973, pág. 701),
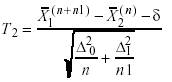
T2 se distribuye aproximadamente tf, donde,
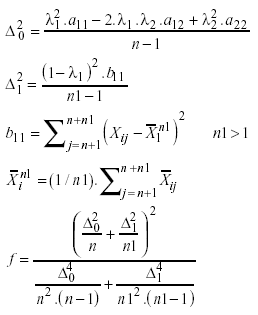
(c) Estadístico T3, tomado de Lin y Stivers (1974, pág. 329),
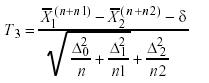
T3 se distribuye aproximadamente tf, donde
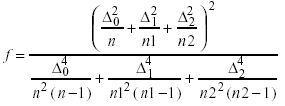
Anderson, A. B., Basilevsky, A. y Hum, D. P. J. (1983). Missing data: a review of the literature. En P. H. Rossi, J. D. Wright y A. B. Anderson (eds). Handbook of Survey Research. Nueva York: Academic Press.
Bhoj, D. S. (1978). Testing equality of means of correlated variates with missing observations on both responses. Biometrika, 65(1), 225-228.
Botella, J., León, O., San Martín, R. y Barriopedro, M. I. (2001). Análisis de Datos en Psicología I (2ª ed). Madrid, Pirámide.
Cohen, J. (1977). Statistical Power Analysis for the Behavioral Sciencies. Nueva York: Academic Press.
Cook, T. D. y Campbell, D. T. (1979). Quasi-experimentation design and analysis issues for field settings. Chicago: Rand McNally.
Dempster, A.P., Laird, N. M. y Rubin, D.B. (1977). Maximum likelihood estimation from incomplete data via the EM algorithm (with discussion). Journal of the Royal Statistical Society, B39, 1-38.
Dempster, A. P. y Rubin D. B. (1983). Overview. En W. G. Madow, I. Olkin y D. B. Rubin (eds). Incomplete Data in Sample Surveys. Vol. II: Theory and Annotated Bibliography. Nueva York: Academic Press, 3-10.
Ghosh, B.K. (1975). On the distribution of the difference of two t-variables. Journal of the American Statistical Association, 70(350), 463-466.
Graham, J. W., Hofer, S. M. y Piccinin, A. M. (1994). Analysis with missing data in drug prevention research. En L. M. Collins y L. A. Seitz (eds). Advances in data analysis for prevention intervention research (pp. 13-63). Washington, D. C.: National Institute on Drug Abuse.
Kalton, G. y Kasprzyk, D. (1986). The treatment of missing survey data. Survey methodology, 12(1), 1-16.
Lewis, P. A. y Orav, E. J. (1989). Simulation Methodology for Statisticians, Operation Analysts, and Engineers. Pacific Grove, Cal.: Wadswoth & Brooks/Cole.
Lin, P. (1973). Procedures for testing the difference of means with incomplete data. Journal of the American Statistical Association, 68, 699-703.
Lin, P. y Stivers, L. E. (1974). On differences of means with incomplete data. Biometrika, 61(2), 325-334.
Little, R. J. A. y Rubin, D. B. (1987). Statistical Analysis with Missing Data. Nueva York: John Wiley & Sons.
Mehta, J. S. y Gurland, J. (1969a). Testing equality of means in the presence of correlation. Biometrika, 56(1), 119-126.
Mehta, J. S. y Gurland, J. (1969b). A test for equality of means in the presence of correlation and missing values. Biometrika, 60, 211-213.
Morrison, D. F. (1973). A test for equality of means of correlated variates with missing data on one response. Biometrika, 60(1), 101-105.
Navarro, J. B. y Losilla, J. M. (2000). Análisis de datos faltantes mediante redes neuronales artificiales: un estudio de simulación. Psicothema, 12, 503-510.
Navarro, J. B. y Losilla, J. M. (2001). Aplicación de redes neuronales artificiales para el análisis de datos con información faltante. Metodología de las ciencias del comportamiento, 3(1), 67-80.
Orme, J. G. y Reis, J. (1991). Multiple regression with missing data. Journal of Social Service Research, 15, 61-91.
Pardo, A. y San Martín, R. (1998). Análisis de Datos en Psicología II (2ª ed). Madrid, Pirámide.
Redman, T. C. (1992). Data quality: management and technology. Nueva York: Bantam Books.
Schafer, J. L. (1997). Analysis of incomplete multivariate data. Londres: Chapman and Hall.
Aceptado el 7 de septiembre de 2001