Psicothema was founded in Asturias (northern Spain) in 1989, and is published jointly by the Psychology Faculty of the University of Oviedo and the Psychological Association of the Principality of Asturias (Colegio Oficial de Psicología del Principado de Asturias).
We currently publish four issues per year, which accounts for some 100 articles annually. We admit work from both the basic and applied research fields, and from all areas of Psychology, all manuscripts being anonymously reviewed prior to publication.
Psicothema, 1992. Vol. Vol. 4 (nº 1). 183-196
Orfelio G. León y Hilda Gambara
Facultad de Psicología , Universidad Autónoma de Madrid
To describe the attitudes of subjects toward risk, Lopes proposed the two-factor model (SP/A): The work presented here uses this model as a framework. It suggests a series of modifications of the stimuli used for data collection and of the measurement of the basic attitude of the subjects toward risk with those stimuli. However, the central scope of the present work is in the formalization of the two-factor model. Also, it is developed and tested empirically through a linear additive model. The results obtained indicate that the modifications in the material used do not alter the response patterns, and that they are compatible with the proposed model.
Key words: Decision making under risk, risk aversion, two factor model of risk.
Actitud hacia el riesgo: propuesta de formalización del modelo de dos factores de Lopes. Para describir las actitudes de los sujetos hacia el riesgo, Lopes (1987) propone el modelo de los dos factores (SP/A). El trabajo que aquí se presenta se contextualiza dentro del mencionado modelo. Se sugieren una serie de modificaciones en cuanto a los estímulos utilizados para la recogida de los datos y a la medida de la actitud básica de los sujetos hacia el riesgo con dichos estímulos. Sin embargo, el eje central del trabajo está en la formalización del modelo de los dos factores; se desarrolla y se contrasta empíricamente un modelo lineal aditivo. Los resultados obtenidos indican que las significaciones en el material utilizado no alteran los patrones de respuesta, y son compatibles con el modelo propuesto.
Palabras Clave: Decisión con riesgo, aversión al riesgo, modelo de riesgo de los dos factores.
The present article, whose principal objective is to propose a formalization of Lopes' (1987) model, is organized in the following manner. First, the model is presented in a simplified form. Second, after describing the experimental paradigm habitually used, a series of modifications will be proposed. Third, a proposal for formalization of the model will be developed. Then the experimental method used will be detailled, in order to prove the necessary assumptions, to estimate the parameters and to empirically test the model. Finally, the results obtained will be discussed and there will be some reflections on the implications of these results in relation to further investigations.
TWO-FACTOR MODEL
Lopes (1987) proposes a description of the subjects' preferences toward risk, based on two, not necessarily independent, factors which are: the dispositional factor and the situational factor.
The first factor would reflect a basic attitude toward risk and would be represented by two polar opposites: security as opposed to potentiality. When there is selective attention paid to the worst results of a set of possible alternatives, what is being sought is security, whereas, on the other hand, when attention is centered on the best results, potentiality is favored. Based on this factor, subjects can then be classified as risk-averse and risk-seeking. The former are those who present an aversion toward risk and whose principal motivation is security, while risk-seeking subjects act guided by the seduction of potential good results.
The second factor, called the aspiration level, represents the situational factor. Ibis factor is determined by the immediate necessities and opportunities for the achievement of the goal set by the subject. In other words, this factor is based on external demands.
Several experimental studies have brought out the presence of both factors. With respect to the first of them, León and Lopes (1988) and León and Gambara (in press) have pointed out the existence of the previously mentioned pattern of risk-seeking and risk-averse subjects. Moreover, Lopes and Schneider (1987) and León and Dueñas (1989), have studied the effects of the aspiration level of subjects in relation to their preferences toward risk.
In general terms, Lopes' model (SP/A: Security-Potentiality/Aspiration) establishes that a relationship exists between the two factors, which does not necessarily has to be independent, and which would explain the behavior of subjects in decision-making involving risk.
EXPERIMENTAL PARADIGM
The experimental paradigm proposed by Lopes (1984), and used by the authors who have worked with this model, will be described.
The stimuli normally used are a set of six lotteries with multiple results (Lopes, 1987), all of them with the same expected value (see exhibit 1).
All possible combinations of pairs of the six lotteries are formed, totalling 15. The task which subjects must perform is to choose one of the lotteries of each pair. Concretely, the subjects averse to risk establishes the following order of preferences: RL > SS > PK > RC > BM > LS [RL: Riskless, SS: Short Shot, PK: Peaked; RC: Rectangular, BM: Bimodal and LS: Long Shot] (see, for example, Lopes, 1984: Schneider and Lopes, 1986).
Attitude toward risk, that is, the classification of risk-seeking and risk-averse subjects, has been established based on the choices made between the two lotteries with the highest risk (BM and LS, specifically). Therefore, a subject is considered to be risk-seeking if his number of choices in these lotteries is equal to or more than 3 (note that 2.5. is the indifference point). On the other hand, a subject is risk-averse if his score on the same lotteries is equal to or less than 2. This criterion or a similar one, has been used in the studies by León and Lopes (1988), León and Dueñas (1989), and León and Gambara (in press).
We propose a series of modifications of the stimuli as well as of the measurement procedure used for the classification of attitudes toward risk, which we will describe as follows.
As the stimuli used, we propose to modify the lotteries with the objective of simplifying the structure and the value of the prizes used; doing so it will be able to elaborate, for future experiments, stimuli that are easier to process and more ecological. However, it is desirable that they maintain similar preference patterns, in order to continue comparison of results between various experiments.
Taking into consideration the aforesaid, we constructed a set of six lotteries, all with the same number of prizes, that is, five. The choice of the number of prizes was not arbitrary in that, although we tried to simplify the stimuli, we also assured that the information was presented in an orderly manner with respect to a central point. The reason for this was to provide the subjects with a more closely adjusted evaluation of the series of prizes presented in each lottery.
Summing up the characteristics of these new lotteries, all of them have the same expected value of 2000 pesetas, the number of tickets in each of them has been reduced from 100 to 20, and a slope between the analogous prizes established by Lopes is maintained. These stimuli can be found in exhibit 2.
The second modification refers to measurement of risk, as deduced from the subjects' preferences.
Before going on to describe this new definition of measurement, we will justify the change. The motivation emerges, on the one hand, from the need to define a measurement of subjects' attitude toward risk empirically and not by following a purely theoretical procedure as has been done up until now. On the other hand, definition of a continuous measurement of risk is needed.
In order to obtain this measurement, we propose to proceed in the following manner. A sample is defined, of which preference for the new pairs of lotteries (number of times each was chosen) is measured.
In strictly operational terms, we consider lotteries to be "riskless" when they are chosen by the population more than 2,5 times; this is the indifference point. Since each lottery is presented in 5 combinations and, therefore, the maximum number of times it can be chosen is 5 and the minimum 0, 2,5 is the mean value. When a lottery is chosen less than 2,5 times, it is defined as "risky".
We will name the preferences of the subject population of the new lotteries as the "base line". If these lotteries maintain properties similar to the lotteries elaborated by Lopes, we will find that the lotteries with the names "riskless, peaked, and short-shot (RL, PK, and SS) remain above the indifference point. On the other hand, the lotteries with the names "rectangular, bimodal, and long-shot" (RC, BM, and Ls) will be found below that point.
The measurement of risk proposed is the following:
Ri. = [(-ZRL) + (-ZPK) + (-ZSS) + ZRC + ZBM + ZLS]/2
For subject "i" (under any aspiration level condition) risk deduced from the preferences is done relative to the average population pattern in terms of their standard scores.
The logic of this measurement is explained as follows. We will first observe the "risky" lotteries (those below the indifference point). A standard positive score in these lotteries indicate that the subject is more risk-seeking than the average population. A standard negative score indicates the contrary.
In the "non-risky" lotteries, a standard positive score indicates that the subject is more risk-averse than the average population. However, if they choose these lotteries fewer times than the average population, a negative standard score will be obtained. For this reason, to obtain the global score of a subject in the lotteries, we multiply the standard scores for "non-risky" lotteries by (-1).
Hence, the subjects' preferences are defined as the sum of the scores in the "non-risky" lotteries (multiplied by -1) and the "risky" lotteries. We divide the sum by two, since each time one lottery is chosen, another is not chosen; by dividing by two we avoid computing the change twice.
For example, a subject who is more risk-seeking than the average population may present the pattern illustrated in exhibit 3.
And therefore his/her risk score corresponds to:
Ri.= 1/2 [-(-0.5/SRL)+ 0+ 0+ 0+ 0+ (-0.5/SSL)] > 0
However, a subject more risk-averse than the population may show the pattern seen in exhibit 4.
The risk score for this subject would be less than 0, since:
Ri. = 1/2 [-(0.5/SRL )+ 0+ 0+ 0+ 0+ (-0.5/SLS)] < 0
FORMALIZATION OF THE SP/A THEORY
With the modifications which were just introduced, we are in a position to develop our central objective: to propose a formalization of Lopes' SP/A Theory (1987) and to test it emperically. As was already pointed out at the beginning of the introduction, according to Lopes, preference for risk can be described, in relation to two factors: security/potentiality and aspiration level. This theoretical model can be expressed as follows:
Rij=f(SPi, Aj, SPAij)
Where Rij represents the risk in the pattern of preferences for lotteries presented to subject "i" in situation "j".
SPi: attitude towards risk of a subject "i".
Aj: effect of a specific situation: aspiration level factor.
SPAij: effect of the interaction between both factors.
The formalization of the model will be analogous to ANCOVA with repeated measurements.
Assumptions
(1) The relationship between risk (Rij) and the SP factor is linear. In addition, the slopes of the regression line of risk (R) on the dispositional factors (SP), for different aspiration levels (A), should be equal.
(2) The interaction term SPAij is equal to zero.(1)
(3) The effects of the different levels of A add up to zero.
(4) The errors are independent and distributed N(0, α).
Formalization of the model
Given the assumptions, we will proceed to develop the model.
First the following regression line is introduced:
R'i.= Bo + B SPi. (equation 1)
That is, we predict risk from the score on the security/potentiality factor.
Subject errors or residuals are defined as the difference between the empirical scores for risk (Rij) and the predicted score (R'ij)
rij = Rij- R’ ij)
For different aspiration level situations, these errors will precisely reflect the part of subject preference due to this factor; that is, the part cannot be explained by the score on the SP factor, but variations in this part of the score are due to the effects of aspiration level Bj, as well as to a certain individual component "ai". To fulfill the second assumption, the effects of these two components should be additive (which will be verified through the non-additivity test of Tukey).
Further, the residuals can be broken down into:
Rij = (μ - μ’) + αi + βj
+ eij
(additive model)
Where (μ - μ’) = represents the global mean of residuals which equals 0.
αi = represents the effect of subject.
βj = reflects the effect of the aspiration level factor (A)
eij = error
And therefore,
rij = αi + βj + eij [ equation 2 ]
The estimates of the effects will be:
μ = R...
![]() i = ri. – r.. = ri . [ equation 3 ]
i = ri. – r.. = ri . [ equation 3 ]
![]() j = r.j – r.. = r.j [ equation 4 ]
j = r.j – r.. = r.j [ equation 4 ]
Therefore, the origin of the regression line (equation 1) will be estimated by:
B0 = R.. – B SP
Substituting in the regression line:
R'i. = (μ- B SP..) + B SPi. [equation 5]
On the other hand, the empirical preference scores can be written as predicted scores plus an error.
Rij = R’ ij + rij
Now substituting the residuals (equation 2) and the predicted scores (equation 5), and reordering terms:
Rij = αi + βj + eij+ (μ - B SP..) + B SPi.
Rij = μ + αi + (βj - B SP..) + B SPi + eij
In the case that αi were not zero (which could be verified empirically analysing the subject factor) the individual differences in risk would be included in the error "eij". Taking into account that the term "B SP.." is a constant for the different variations of Bj, we can rewrite equation 6 as follows:
Rij = μ + βj + B SPi + eij
Where μ = the global mean of risk for all subjects in situations "j".
Bj = the effect of the aspiration level factor.
B = the slope of the regression line of risk over the SP factor.
SPi. = Subjects'scores in the security/potentiality factor.
eij = errors.
TESTING THE MODEL
We will use the method being described in the following section to confirm the necessary assumptions of the proposed model, to estimate its parameters, and to contrast it.
METHOD
Subjects
We began with a set of 389 subjects, who, in experimental terms, will be the population. All of them were first-year students of Psychology at ‘Universidad Autónoma de Madrid'. The experimental group was a random selection of 54 subjects, from the population.
Stimuli
The stimuli were several series of lotteries; specifically, three sets of six lotteries each were used. The lotteries which made up the first set (C1) all presented the same expected value [E (x)=2000 pesetas]. The second (C2) and third (C3) sets were made up of lotteries with expected value ranging from 2000 pesetas for the "riskless" lottery, to 4000 pesetas for the "long-shot" lottery (and all between 2000 and 6000), respectively.
The set of lotteries C1 was described in the introduction and is represented in exhibit 2.
Sets C2 and C3 represent manipulation of the aspiration level factor. Except for their expected value, these lotteries also vary on the characteristics indicated on previous pages. Exhibits 5 and 6 show these lotteries.
Within the complete set of lotteries with equal expected values, C1 (base line) will measure the SP factor. Therefore, the subjects' preference for the lotteries will express the basic attitude toward risk on the security/potentiality factor, that is, Rij will be the estimation of SPi . (Assuming the value of factor A to be, as the reference point, zero).
For the C2 and C3 lotteries, an attempt was made to manipulate the aspiration level by modifying the expected values. Doin so, risk expressed by subjects in the lotteries will reflect variation in the SP and A factors.
Design and procedures
In the first session the population preferences were measured for the set of lotteries C1. Two weeks later, the experimental sample made up of 54 subjects, once again expressed their preferences for lotteries, this time for sets C2 and C3. In the second session there were 60 pairs of lotteries, since each possible pair was presented twice (once to estimate the model and the other time to test the model). The two sets of similar data were obtained to use one of the sets to estimate the parameters of the model, and later, to see the goodness of fit in the second set, avoiding bias in the adjustment because of the use of the same data. The order of presentation of the lotteries was totally random:
The students (in the population as well as in the experimental sample) carried out the task collectively. The 15 possible pairs of lotteries were presented to subjects using transparencies. Each pair was presented in a vertical position, one on top of the other. The subjects had to indicate their responses on an answer sheet, marking their preferences for each pair of lotteries, circling either an "S" (the lottery presented in the upper position) or an "I" (the one in the lower position). The order of presentation within pairs was also totally random.
At the beginning of each session, a careful explanation of the task and of the significance of the lotteries was given. In summary, the subjects were told to indicate which lottery of each pair they would choose if they were given the possibility to play one of them only once. The first session (base line) lasted approximately fifteen minutes; the second (experimental task) about thirty minutes.
The data obtained, for the experimental sample, were the following: (1) scores on SP for C1, (2) risk for C2 and C3 (data to be used for estimating the parameters of the model), (3) risk for C2* and C3* (data to test the model).
RESULTS
The results are presented in the following way: firstly, a series of basic results on the modifications of the experimental paradigm will be presented. Secondly, the results on the verification of the assumptions will be presented. Thirdly, the model will be estimated. Finally, the result of the test of the model will be presented.
Basic Data
The results are compared with other results obtained in studies where traditional lotteries were used earlier. (León and Lopes, 1988, and Lopes & Schneider,1987).
As can be seen, the preferences found with the new lotteries are similar to those obtained previously with traditional lotteries.
2. In exhibit 8, the means and deviations of risk scores (Rij) of the experimental subjects are represented for all three sets of data: C1 -base line- C2 and C3.
To analyse the effects of the experimental manipulation, we proceeded with an ANCOYA, using the scores in SP as the covariable.
lt was verified that the experimental manipulation produced a significant effect on risk expresed in sets C2 and C3. (F1,53 = 7.69. p< =.0077)
Verification of Assumptions
1. In relation to assumption (1), we calculated the linear correlation between SPi (scores on the security/potentiality factor for the experimental sample) and Rij (preferences from this sample for C2 and C3).
We found, for both situations, correlations above .60. Specifically, for C2 the correlation was .681 and for C3 it was .660. Therefore, Rij correlates approximately linearly with SPij. The equality of slopes was verified by carrying out the analysis of the covariance al specified in section 1.2. We found non-significant difference between regression coefficients (F1,52=.834).
2. Assumption (2) was verified by means of Tukey's non-additivity test for residual scores, and non-additiveness was not rejected. (F1,51 = .395). Consequently, the model is additive.
3. Assumption (3) was evident from the means of the estimated effects of A.
( ![]() j = r.j - r..)
j = r.j - r..)
4. The independence and normality of eij was not verified. It is assumed that these assumptions do not have any influence, as is usual in ANOVA.
Model
1. Previously, the effects of the subjects (considered ramdomly as usual) on the residual scores were verified (F53,53 = 5.3203; p < 0.04). Therefore, this effect will be included in the error term in the model.
2. The estimates of the parameters of the model are shown in exhibit 9.
Test of the model
1 Results for the replicated sets of data (C2*, C3*), are presented in exhibit 10.
2. We contrasted the adjustment of the model using the statistic of multiple regression (Tabachnick and Fidell, 1983).
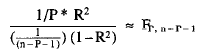
Were P* = the number of parameters of the model.
We obtained
F3,104 = 32.1104; p <.001
To obtain more information on predictive power of the model, we proceeded as follows:
We categorized the values of risk into three groups. The first category includes those subjects whose risk factors were between -2 and 0, and therefore dealt very clearly with risk-averse subjects. We must remember that this assumed that this group had the most conservative patterns of choice in the whose population. The range of risk goes from -2 to 7. Since the interval [-2 ; 0] includes more ‘risk-averse' subjects than the average, subjects with scores from 0 to 7 are more ‘risk seeking' than the former. Since this is a wider category, we decided to divide it into two categories. Hence, in a second category, we include moderately risk-seeking subjects, whose preference scores varied from 0 to 3.5. Finally, the risk-seeking subjects were those with scores between 3.5 and 7.
Based on this categorization, we constructed a contingency table for all data (exhibit 11). The columns represented the model predictions; the lines represented empirical data.
In exhibit 11, the information is presented in a direct way. In one of the principal diagonals the agreement between the model and data can be seen. In all, the agreement was equal to 66,7%.
CONCLUSIONS
First, in this paper we proposed the use of a set of new stimuli. Our objective was to make them simpler in structure than the lotteries presented by Lopes (1984), so that they are easier to handle in experiments and data analyses. However, the new lotteries should continue to maintain their basic property; that is, they should present a pattern of choices which point out differences in risk associated with each lottery. The results presented in exhibit 7 showed that this objective was reached.
Second, a new measurement of subjects' attitudes toward risk was suggested. The advantages of this measurement were several: first, it was defined as a continuous measurement; (instead of the previous dichotomous approach), and Second, risk was measured for each subject according to the population s/he belongs to and not by some theoretical criterion on the part of the researcher.
The manipulation of the external demand, whose objective is to produce distinct aspiration levels, was carried out by modifying the expected values of the lotteries. To determine the adequate experimental manipulation, it was found that the greater the expected values of the lotteries, the greater the number of choices, and, therefore, the higher the score on the risk measurement in relation to the base line (equal expected value). As could be seen in exhibit 8, the mean scores for risk increased from the C1 lottery (base line) to the lotteries with greater expected value, these differences being significant. Therefore, sensitivity on the part of the subjects toward external demand can be observed (León and Dueñas, 1989; Lopes and Schneider, 1987).
As for the model itself, we analysed, in the first place, the advantages of formalizing Lopes'(1987) two-factor theory mathematically. Secondly, we reflected on the implications of the model with respect to the underlying theory.
The main contribution of the formalization of the model is the ability to quantify the distinct elements of the subjects' attitudes toward risk. Although Lopes' theory described a relationship between the subjects' preferences toward risk and the dispositional factor, nothing was mentioned as to the nature of that relationship. Now we have found that that relationship is, to a large degree, linear (approximate correlation, 65.). On the other hand, the model, just as we had proposed, requires that the interaction between the factors be zero (a supposition which we were able to confirm). The underlying theory allows the situational and the dispositional factors not to be independent. However, Lopes drew no conclusions from this, leaving unspecified as to how this interaction should take place. Neither can we demonstrate, on the basis of this study, the absence of such interaction. What we do propose, however, is an absence of interaction in the experimental manipulations in this study, or similar studies. Moreover, we must take into account the fact that, an SPAij = 0 would force the mathematical model to estimate the interaction for each of the subjects, which would increase the complexity of the model and the necessity of theoretical explanation of the interaction. One of the most interesting results is, we believe, the fact that a subject effect exists that cannot be explained by the dispositional factor (SP) - see section 3.1. This is an element not predicted by the theory that is, there are still individual differences due to causes unforeseen by the theory. These differences could be due to different processing strategies, or to a certain personal characteristic, different from attitude toward risk.
In regard to the validity of the model, we have found a proportion of explained variance of approximately .48. We must point out any previous indicative index of the explicative content of the two factor theory has lacked. Moreover, in more applied terms, the predictive power of the model (percentage of agreement between the model and empirical data in the categories), was found to be relatively high -67%-.
Summing up, we can state that, with the formalization of the SP/A theory, we have been able to determine a measurement with explanatory value. For experimental tasks with lotteries, the factors of the theory allow a large degree of explanation, although some systematic individual differences still appear, which cannot be attributed to error.
AKNOWLEDGEMENTS: This study was supported by the M.E.C. "Programa Sectorial de Promoción General del Conocimiento (Grant PB 88-0183)". The authors wish to acknowledge the important contribution of Edita Montarelo and Marisol Diez. Also, we wish to thank the valuable contribution of two anonimous referees over a previous version on this paper.l
FOOTNOTES
(1).- For reasons of parsimony in the formalization of the model, we have requiered that the interaction be null. This assumption will be tested.
REFERENCES
León, O.G. and Dueñas, MªS. (1989). Flexibilidad y actitud al riesgo. Boletín de Psicología, 24, 47-61.
León, O.G. and Gambara, H. (1991). Fulfillling prophecy and feedback in decision making under risk. Psicothema, 3, 219-230.
León, O.G. and Lopes, L.L. (1988). Risk preference and feedback. Bulletin of the Psychonomic Society, 26(4), 343-346.
Lopes, L.L. (1984). Risk and distributional inequality. Journal of Experimental Psychology: Human Perception and Performance, 10, 465-485.
Lopes, L.L. (1987). Between hope and fear. The psychology of risk. Advances in Experimental Social Psychology, 20, 255-295.
Lopes, L.L. and Schneider, S.L. (1987). Risk preference and aspiration level. Journal of Experimental Psychology: HP and P, 12(4), 535-548.