Psicothema was founded in Asturias (northern Spain) in 1989, and is published jointly by the Psychology Faculty of the University of Oviedo and the Psychological Association of the Principality of Asturias (Colegio Oficial de Psicología del Principado de Asturias).
We currently publish four issues per year, which accounts for some 100 articles annually. We admit work from both the basic and applied research fields, and from all areas of Psychology, all manuscripts being anonymously reviewed prior to publication.
Psicothema, 1995. Vol. Vol. 7 (nº 1). 159-171
Antonio Solanas y Vicenta Sierra
Universidad de Barcelona
El análisis de incrementos-decrementos fue investigado en un amplio estudio de simulación Monte Carlo. Se demostró que la violación de supuestos produjo problemas en la inferencia, observándose una importante discrepancia entre las tasas exacta y empírica de error tipo I. La asimetría del término aleatorio del modelo autorregresivo de primer orden afecta dramáticamente la tasa empírica de error tipo I. Se encontró que los niveles de dependencia serial distintos de cero afectaron la tasa empírica de error tipo I, aunque la técnica mostró un nivel aceptable de robustez para valores de autocorrelación cercanos a cero. Extrema precaución es recomendable para utilizar la técnica en el análisis de datos de diseños A-B, donde no es extraño hallar autocorrelación en las series.
Increments-Decrements Analysis. Increments-decrements technique was investigated in an extensive Monte Carlo simulation stud. It was demonstrated that violated assumptions yield problems of inference in the form of important differences between exact and empirical type I error rates. Skewness in random error of first order autoregressive model affects dramatically empirical type I error rate. It was found that the empirical type I error was affected by nonzero serial dependence, although this technique showed an acceptable robustness for leeels of autocorrelación near zero. Extreme caution is recommended for use this strategy in A-B designs where autocorrelated series are not unusual.
El análisis de datos procedentes de diseños conductuales se fundamenta, generalmente, en la denominada inferencia visual. Esta estrategia se ha difundido extensamente y relegado a un segundo plano el análisis estadístico, tanto en el ámbito básico como en el aplicado, aunque son numerosos los problemas en el estudio visual de diseños conductuales (Ballard, 1983; Jones, Weinrott & Vaught, 1978; Wampold & Furlong, 1981). El acuerdo entre jueces, cuando se fundamenta el análisis en la inferencia visual, es escaso, agravándose con la existencia de dependencia serial en los datos: además, la estrategia de los evaluadores está fuertemente ligada a su formación y no es fácil sintetizarla en un conjunto de reglas.
Las anteriores consideraciones pretenden destacar aquellos inconvenientes más destacables, máxime cuando disponemos de numerosas técnicas estadísticas especialmente ideadas para el análisis de datos procedentes de diferentes tipos de diseños conductuales (Edgington, 1967; 1980a; 1980b; Revusky, 1967; White, 1974). Este último grupo de técnicas cobra importancia debido a la imposibilidad de recurrir a pruebas estadísticas clásicas (T-TEST, ANOVA, etc...), ya que los datos obtenidos longitudinalmente presentan dependencia serial, violándose los supuestos necesarios para su utilización. Es posible abordar la evaluación de la incidencia del tratamiento recurriendo al análisis de series temporales, pero el número de datos que son necesarios para una aceptable estimación de los diferentes parámetros supera el número de mediciones realizadas en la mayoría de investigaciones, tanto básicas como aplicadas.
En los estudios conductuales aplicados existen dificultades añadidas, pues no es posible controlar totalmente el amplio número de variables contaminantes y, en general, este motivo es suficiente para cuestionar el carácter experimental de un amplio grupo de investigaciones. Por otro lado, no es inusual la existencia de dificultades para obtener datos que, en casos extremos, limitan el número de mediciones en la fase A a tan solo un valor. La técnica estadístico βn (Solanas, Salafranca y Guárdia, 1992) fue ideada para el análisis estructural de diseños A-B con un solo dato en la fase A. En lo sucesivo, nos referiremos a esta estrategia como análisis de incrementos y decrementos. Un antecedente de esta técnica se halla en Moore y Wallis (1943), trabajo en el cual se desarrollan un amplio grupo de técnicas para analizar la aleatoriedad de las series. El análisis de incrementos y decrementos toma la idea de aleatoriedad para realizar un análisis estructural de la serie, frente al habitual estudio comparativo de niveles de conducta entre fases.
En el presente trabajo reconceptualizamos el análisis de incrementos y decrementos, estudiando el impacto de la violación de supuestos sobre la tasa empírica de error tipo I. En concreto, nos interesamos por la violación de la independencia serial y simetría del término error, evaluando su incidencia sobre la tasa empírica de error tipo I. Además de consideraciones de orden teórico, existen investigaciones previas (Crosbie, 1987; 1989), realizadas sobre otras técnicas estadísticas, donde se muestra el fuerte impacto sobre la tasa empírica de error tipo I ante la violación del supuesto de independencia. lgualmente, la violación del supuesto de simetría debe alterar la tasa empírica de error tipo I respecto a la tasa exacta. En ambos casos, nuestro objetivo consistió en determinar la magnitud de la alteración en el análisis de incrementos y decrementos.
Análisis de incrementos y decrementos: reconceptualización
En todo momento nos referiremos a un diseño conductual A-B con un único dato en la fase A. Modelizaremos el diseño anterior, bajo el supuesto de no incidencia del tratamiento, como un proceso aleatorio, donde para todo Δt se mantiene que
![]()
para cualquier Δx. De la expresión anterior se desprende que, aunque la función de distribución F(Δ x) se desconozca, debe aceptarse su simetría para todo momento t.
Sobre Δx, que denotaremos mediante ε, imponemos determinadas condiciones:
![]()
en todo momento t y para cualquier valor k. Respecto al término error ε, debe advertirse que no se exige que la varianza sea constante en todo momento (no se requiere que el proceso sea estacionario en varianza), aunque ésta debe ser finita. Este hecho añade generalidad, por lo cual no tiene consecuencias en la técnica expuesta la más que probable inconstancia de la variabilidad de la conducta a lo largo del tiempo.
En la investigación conductual el interés puede consistir en determinar si el tratamiento incrementa o decrementa la tasa o el nivel de conducta. Tradicionalmente, el enfoque estadístico se ha centrado en determinar si entre fases adyacentes se ha producido un cambio de nivel, independientemente de que éste se produzca mediante un cambio abrupto o progresivo. De forma alternativa, puede analizarse la incidencia del tratamiento a partir de la estructura incremental o decremental, según sea el caso, de la serie. Esta última estrategia supone que los cambios son progresivos; por tanto, el análisis de las diferencias de primer orden de la serie deben reflejar si el comportamiento muestra cambios, ya sean en sentido incremental o decremental.
La estrategia de análisis de la eficacia o no de intervención aquí expuesta no es incompatible con aquellas fundamentadas en la comparación de niveles de conducta, sino complementaria. Pueden existir situaciones en las cuales los cambios de la conducta sean abruptos, donde estadísticos de estructura no son adecuados; pero es posible que la modificación producida por la intervención no se refleje en cambios de nivel, sino en el patrón de incrementos-decrementos de la serie, casos en los cuales los estadísticos de nivel no son pertinentes (la Figura 1 muestra un ejemplo en el cual el análisis de incrementos y decrementos detecta una estructura incremental en la serie, aunque el proceso parece estable en media).
Para realizar la formalización estadística de las anteriores ideas, considérese la serie X1A, X2B, ... , XnB como datos de un diseño A-B con un solo dato en la fase A. Puesto que los tratamientos pueden incidir incrementando o decrementando la conducta, se diferenciará entre ambos casos. Nos referimos al análisis incremental cuando el cambio esperado por la acción del tratamiento se traduce en el aumento de la conducta. La hipótesis nula, suponiendo la aleatoriedad de la serie, es
![]()
Definamos βn como,
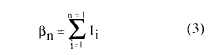
donde Ii denota la función indicadora, que, en el análisis incremental, toma valores según el siguiente criterio
I i = 1 , si
X i+1 > X i
Ii = 0 , en cualquier otro caso (4)
La razón βn /(n-1) estima la probabilidad de incremento, dadas dos observaciones adyacentes. El contraste de la hipótesis nula puede realizarse sobre la mencionada proporción o sobre el valor βn. En ambos casos la distribución binomial es el modelo de probabilidad adecuado para obtener la probabilidad asociada al estadístico. Sólo porque requiere menos cómputo (aunque la diferencia es despreciable) proponemos realizar el contraste sobre βn, considerando el modelo de probabilidad Bi(n-1, 0.5), siendo E(βn) = (n-1)/2 y su varianza Var(βn) = (n-1)/4, siempre bajo el supuesto de hipótesis nula. La siguiente expresión proporciona la probabilidad asociada
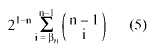
Cuando el cambio esperado por la acción del tratamiento sobre la conducta sea la disminución de la misma, nos referiremos al análisis decremental. La hipótesis nula es
![]()
Para βn obtener la función indicadora toma valores, en el caso del análisis decremental, según la regla
I i = 1 , si X i+1 < X i
Ii = 0 , en cualquier otro caso (7)
El cálculo mediante la expresión (5) puede resultar pesado, aunque se puede realizar mediante alguno de los programas de aplicación estadística comercializados.
En cualquier caso, si el número de datos n es suficientemente elevado, es posible simplificar el cómputo mediante la aproximación normal de la distribución binomial, obteniéndose la significación mediante.
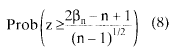
aunque el número de datos habituales en las investigaciones no aconsejan utilizar la aproximación propuesta, pues, para un número reducido de observaciones, existe excesiva diferencia entre la probabilidad asociada al estadístico obtenida con (8) y el valor exacto. Aunqque desaconsejamos la aproximación, si nos atenemos a los requisitos tradicionales, puede utilizarse (8) cuando se cumple βn ≥ 5 y n - βn - 1 ≥ 5.
Estudio de la violación de supuestos: simulación Monte Carlo
Nos referiremos a los distintos supuestos implícitos en el análisis de incrementos y decrementos, en extremo importantes para garantizar que la tasa de error tipo I empírica se mantenga dentro de los límites admisibles y se corresponda con la tasa exacta. Como ya se ha explicitado, se requieren los supuestos de simetría de F(ε) y la no existencia de dependencia entre observaciones consecutivas. La violación de estos supuestos, desde una perspectiva teórica, deben alterar la probabilidad asociada al estadístico y, por tanto, la tasa empírica de error tipo I. En la presente investigación analizamos el efecto de la asimetría y la autocorrelación sobre la tasa empírica de error tipo I, estimando, mediante simulación Monte Carlo, la magnitud del efecto de esta fuente de error estadístico.
Procedimiento
Las series se generaron mediante simulación Monte Carlo, con longitud, dependiendo del subexperimento, de 6, 11 o 21 datos, que incluyen los datos de ambas fases. Estos valores fueron seleccionados por dos motivos: a) n = 6 es el número mínimo de observaciones necesarias para obtener niveles de significación inferiores a 0.05 para el estadístico; b) los tres tamaños de serie establecidos recogen la gama de observaciones típicas en diseños conductuales A-B en investigaciones aplicadas. Se establecieron diferentes niveles de Φ1(-0.9 a 0.9, incremento de 0.1), a fin de evaluar el efecto de la dependencia serial sobre la tasa empírica de error tipo I. Cada dato se obtuvo según la siguiente expresión
Xi+1 - Xi = Φ 1 X i + ε i+1
donde E(ε) = 0 y Var(ε) = σ2 son constantes para todo momento, especificándose tres condiciones para F(ε): uniforme, normal y exponencial. Para asemejar estas condiciones, establecida la restricción E(ε) = 0, se determinaron los parámetros de las distribuciones para que Var(ε) = 1.
Al existir dos análisis posibles (incremental o decremental), las anteriores condiciones experimentales se probaron para ambos casos. Se realizaron 3x19x3x2 = 342 subexperimentos y, en cada uno de éstos se generaron 1000 diseños A-B con un solo dato en la fase A. Para cada serie de observaciones (para todo diseño), los primeros 50 datos no fueron seleccionados, a fin de reducir los efectos artificiales (Greenwood y Matyas, 1990): o sea, mitigar en lo posible la incidencia de valores iniciales (semillas) anómalos del término pseudoaleatorio y estabilizar la serie.
La generación del error aleatorio ε se realizó mediante la función RND del lenguaje de programación BASIC (se utilizó el TURBO-BASIC), que permite obtener números pseudoaleatorios uniformemente distribuídos en (0,1). Se trata de un generador lineal congruencial que, previamente fue probado respecto a diferentes condiciones de aleatoriedad (prueba de frecuencia mediante el estadístico χ2, prueba de la autocorrelación, test de rachas, ajuste a una distribución uniforme mediante la técnica de Kolmogorov-Smirnov y prueba de la mediana), con resultados satisfactorios. En cualquier caso, el principal inconveniente reside en que se trata de un generador con ciclo no excesivamente elevado, y, para mitigar este problema, la semilla se variaba con gran frecuencia en base a lecturas del reloj interno del ordenador. Estos números pseudoaleatorios fueron transformados a variables con distribución uniforme, exponencial y normal mediante la técnica de la inversión, los dos primeros, mientras la última se obtuvo en base a una aproximación racional.
Análisis de datos
Para cada una de las series de datos se calculó el número
de incrementos o decrementos, según el caso. La tasa nominal (αN)
de error tipo I se fijó en 0.05, que corresponde a los puntos de corte
5, 9 y 15 en series de longitud 6, 11 y 21, respectivamente. Se contabilizó
el número de veces que fue superior o igual a los puntos de corte correspondientes
a la tasa nominal establecida. Este último dato, dividido por el total
de muestras Monte Carlo, permitió estimar la tasa empírica de
error tipo I. A partir de la tasa empírica ![]() E estimada se pudo analizar la correspondencia entre valor estimado y
esperado, y conocer la magnitud de la incidencia de la violación de los
supuestos de simetría e independencia. Dada la distribución discreta
del estadístico, es fundamental diferenciar entre las tasas nominal y
exacta de error tipo I, valor, este último, al cual debe ajustarse la
tasa empírica. Las tasas exactas - E son 0.03125, 0.010742
y 0.020694, respectivamente, para series de n = 6, n = 11 y n = 21. Por otro
lado, para determinar si la tasa empírica se corresponde con la tasa
exacta, considerando la fluctuación aleatoria, se determinaron los intervalos,
E estimada se pudo analizar la correspondencia entre valor estimado y
esperado, y conocer la magnitud de la incidencia de la violación de los
supuestos de simetría e independencia. Dada la distribución discreta
del estadístico, es fundamental diferenciar entre las tasas nominal y
exacta de error tipo I, valor, este último, al cual debe ajustarse la
tasa empírica. Las tasas exactas - E son 0.03125, 0.010742
y 0.020694, respectivamente, para series de n = 6, n = 11 y n = 21. Por otro
lado, para determinar si la tasa empírica se corresponde con la tasa
exacta, considerando la fluctuación aleatoria, se determinaron los intervalos,
![]()
donde MC denota el número de muestras Monte Carlo. Se fijó, arbitrariamente, α = 0.05, obteniéndose los intervalos
n = 6, 0.02046 ÷ 0.04203
n = 11, 0.00435 ÷ 0.01713
n = 21, 0.01187 ÷ 0.02951
A partir de estos intervalos es posible determinar si la tasa empírica se mueve dentro de los valores esperados para el valor α fijado.
Complementariamente al análisis descrito, se halló para cada una de las combinaciones de tipo de hipótesis, tamaño de la serie y tipo de distribución del término error (un total de 18 condiciones) un modelo de regresión que permita determinar la tasa empírica de error tipo I en función del valor del término autorregresivo. La inspección de gráficas bivariables mostró que los datos podían ser representados mediante un modelo de crecimiento exponencial
![]()
fijándose de forma arbitraria γ = 0. El análisis de la pertinencia de los modelos mostró una aparente adecuación, estimándose todos los parámetros y determinandose R2, además de la razón F. Debemos notar que, en la medida que la tasa empírica de error tipo I está acotada superior e inferiormente, teóricamente, otros modelos son adecuados; pero en los valores de Φ1 estudiados, no existen indicios de punto de inflexión, por lo cual se optó por la modelización expuesta, únicamente aceptable para los valores -0.9 ≤ Φ1 ≤ 0.9.
Resultados
Respecto a la incidencia de la autocorrelación sobre la tasa empírica de error tipo I, se aprecia (Tablas 1, 2 y 3) un incremento monotónico de la misma, resultado constante para cualquier tamaño de la serie, tipo de hipótesis y distribución del error. Cuando la autocorrelación es negativa se nota la infraestimación de la tasa exacta de error tipo I, mientras para valores positivos se obtienen tasas empíricas de error tipo I infladas. Los niveles moderados de autocorrelación muestran incidencia sobre la tasa empírica de error tipo I, incluso en aquellos casos en que la dependencia serial no dista en exceso de Φ1 = 0; sólo en el rango de valores entre -0.2 y 0.1, considerando únicamente distribuciones del término error simétricas, la autocorrelación no incide en exceso sobre la tasa empírica de error tipo I.
Aunque el tamaño de la serie no cambia notablemente el patrón de resultados, sí es destacable que, cuando n = 11, se observa una mayor proximidad entre la tasa empírica de error tipo I y la tasa exacta. Las Tablas 1 y 2 muestran que, cuando el error posee distribución simétrica, las tasas empíricas de error tipo I se ubican dentro del intervalo de probabilidad que recoge las fluctuaciones aleatorias, sin ser excesivamente rigurosos, para valores de autocorrelación comprendidos entre -0.3 y 0.2 para n=11. En general, la tasa empírica de error tipo I es menor para n = 11 comparativamente a los otros tamaños de la serie considerados en este estudio, aunque este resultado no siempre supone considerar óptima una longitud de serie n = 11.
Como se esperaba, la violación del supuesto de simetría en la distribución del error (Tabla 3) muestra graves consecuencias sobre la tasa empírica de error tipo I, pudiéndose calificar de aberrantes los resultados obtenidos. Destaca la presencia de desajustes entre las tasas empírica y exacta de error tipo I, especialmente cuando los datos fueron generados por un proceso en el cual Φ1 = 0. Por otro lado, el comportamiento de la incidencia de la autocorrelación produce tasas aceptables para niveles positivos en el caso incremental, apareciendo un patrón opuesto cuando se realiza el análisis decremental. La longitud de la serie no muestra importantes diferencias en el patrón de resultados expuesto.
En la Tabla 4 se muestra la información correspondiente a la modelización de crecimiento exponencial realizada. En general, las estimaciones de los parámetros para los casos en los que el término error posee distribución simétrica es similar, sólo dependiendo de la longitud de la serie. Nótese que, aunque en la series de longitud 11 se obtiene la mayor velocidad de crecimiento, sistemáticamente, la estimación del parámetro βo (en algún sentido, un parámetro de magnitud) es inferior. Por otro lado, siempre para distribuciones simétricas del término error, existe una elevada correspondencia entre los valores de βo estimados y las tasas exactas de error tipo I, como era previsible, si el modelo de crecimiento exponencial era una elección adecuada. Los valores F y R2, además de otros datos complementarios (ver Tabla 4), proporcionan información sobre la modelización, aunque debe advertirse que R2 es un indicador excesivamente optimizado. Por un lado, existen sólo 19 pares de datos para estimar los parámetros de la función: por otro, no posee el mismo valor informativo que en regresión lineal, cuando se obtiene para modelos no lineales. Los gráficos donde se muestran los datos empíricos y la función de crecimiento exponencial obtenida, que han sido omitidos por motivos de extensión, muestran una más que adecuada correspondencia entre ambos. También el análisis de residuos mostró la adecuación del modelo.
Cuando el término de error posee una distribución con fuerte asimetría, el modelo de crecimiento exponencial también es adecuado, excepto para la hipótesis decremental con n = 21. En este caso, los datos empíricos muestran un comportamiento más complejo, especialmente entre -0.3 ≤ Φ 1 ≤ 0.3. Es probable que un problema en la ejecución de esa simulación explicara estos resultados, pero difícilmente compatible con los otros datos disponibles; por lo tanto, creemos que la situación se hace mucho más compleja para otros valores no incluídos en este trabajo. Si el término error posee distribución asimétrica, no se observa un mismo patrón de resultados para ambos tipos de hipótesis. Respecto al caso incremental, notamos mayor valor de la velocidad de crecimiento, con estimaciones de βo menores que la tasa exacta; por su parte, en el contraste decremental se observa un patrón opuesto. Esta parece ser la consecuencia más destacable de la asimetría del término error sobre el tipo de contraste realizado. Por otro lado, comprendemos mejor cómo las tasas de error tipo I empíricas tienden a equilibrarse si, para Φ1= 0, muestran un elevado desajuste, hecho que recoge la estimación de βo. La razón se halla en las velocidades de crecimiento diferenciales.
Discusión
Parece incuestionable desaconsejar, tanto por razones de orden teórico como por los resultados obtenidos en la simulación, el análisis de incrementos y decrementos, cuando existan dudas sobre la simetría del término error. El estadístico carece de robustez ante la violación del supuesto de simetría. Desde una perspectiva aplicada, debe evitarse recurrir a esta técnica analítica cuando, dada la existencia de techo y/o suelo en la variable respuesta, el nivel conductual se aproxima, en algún o distintos momentos (especialmente en este último caso) del período de observación, a los máximos y/o mínimos niveles de respuesta.
Respecto al efecto diferencial de la asimetría del término error sobre la tasa empírica de error tipo I, dependiendo de la hipótesis contrastada, los resultados deben ser función del sentido e intensidad de la asimetría, como argumentaremos. En una de las condiciones experimentales del presente trabajo se fijó una distribución exponencial para el término error, que, para cualquier valor del parámetro determinante de la función, posee asimetría positiva (γ1 = 2). Este hecho se traduce en una mayor probabilidad de obtener valores negativos en el término error; por tanto, cuando se contrasta la hipótesis incremental, las series tienden a presentar menor número de incrementos que el esperado, siempre bajo el supuesto de hipótesis nula, existiendo un punto en el cual los valores de autocorrelación positiva compensan este efecto. Si se prueba la hipótesis decremental; la situación se invierte, pues el número de decrementos supera al esperado por azar, dado el supuesto de hipótesis nula, existiendo un punto en el cual los valores de autocorrelación negativa neutralizan este efecto. Por este motivo, el rango de valores de autocorrelación en los cuales se produce un ajuste entre las tasas empírica y exacta de error tipo I se halla desplazado respecto al valor esperado Φ1 = 0, siempre que la distribución del error sea asimétrica. En síntesis, las distribuciones asimétricas positivas del término error conllevarán los resultados obtenidos en la presente investigación, más acentuados cuanto mayor sea la intensidad de la asimetría y por otro lado, amortigüados si la asimetría es inferior a γ1 = 2 por su parte, cuando el término de error presente distribución con asimetría negativa, cabe esperar un patrón de resultados opuesto al hallado en la presente investigación, compensándose la asimetría con valores de autocorrelación negativos para el contraste incremental, mientras la dependencia serial positiva neutraliza el efecto de la asimetría en la prueba decremental.
Aunque esta investigación no fue planificada para estudiar la potencia de la técnica, los resultados que muestran cómo la tasa empírica de error tipo I es infraestimada cuando existe autocorrelación negativa, indican posible pérdida de potencia en estas condiciones. No existe discrepancia, en este punto, con los resultados hallados en otras investigaciones sobre distintas técnicas utilizadas para el análisis de datos de diseños conductuales (Crosbie, 1986; 1987). Por su parte, la presencia de un componente autorregresivo positivo incrementa la tasa empírica de error tipo I, aunque esta tasa se sitúa en niveles más aceptables que los hallados en investigaciones realizadas sobre otras técnicas, como T-test (Crosbie, 1986), Split-middle (Crosbie, 1987) y Estadístico C (Crosbie,1989). Estos resultados no son sorprendentes, puesto que, si la significación del estadístico se fundamenta en la distribución binomial, la presencia de un componente autorregresivo vulnera el supuesto de independencia y, debido a la actuación del mismo sobre la serie, el número de series básicamente incrementales o decrementales será mayor al esperado bajo el supuesto de independencia.
El modelo exponencial parece recoger adecuadamente la relación entre el parámetro autorregresivo y la tasa empírica de error tipo I, proporcionando información complementaria sobre el efecto del tamaño de la serie. Considerando sólo los casos con distribución simétrica del error, los parámetros estimados recogen la similitud observada entre ambos tipos de hipótesis, además de la invarianza respecto a la distribución del error. Para el término error con distribución asimétrica, el patrón es distinto según el tipo de hipótesis considerada; desajuste a la baja entre las tasas exacta y empírica, para hipótesis incrementales, mostrando inversión de la situación, cuando se contrasta la hipótesis decremental.
El modelo fijado en este estudio para establecer la relación entre las observaciones es arbitrario, pues no conocemos el patrón subyacente en el comportamiento humano. Hemos supuesto que la interdependencia existía entre el incremento y el nivel de conducta actual, pero son posibles otras estructuras no estudiadas en este trabajo. Recientemente, a partir de los comentarios realizados por uno de los revisores, probamos el modelo,
Xi+1 - Xi = Φ 1 ( Xi - Xi-1 )+ ε i+1
que corresponde a un ARIMA(1,1,0), donde establecimos δ = 0 (parámetro de nivel). Si el comportamiento es modelizado adecuadamente por la anterior expresión, la incidencia de la autocorrelación sobre la tasa empírica de error tipo I es más notable, como mostró una nueva simulación. También estos resultados aconsejan no utilizar el análisis de incrementos-decrementos cuando exista evidencia o sospecha de dependencia serial.
El análisis de incrementos-decrementos aplicado a diseños A - B con un solo dato en la fase A presenta un problema insalvable, consistente en la imposibilidad de conocer la existencia de tendencia en la fase de línea base. Sólo si la tendencia en la fase A es opuesta a la dirección del cambio esperado por la acción del tratamiento o la línea base es estacionaria, está justificado utilizar esta herramienta de análisis de datos. Difícilmente es posible determinar el patrón de conducta en la fase de pre-tratamiento, si tan solo se posee una observación; por tanto, únicamente es factible recurrir a la búsqueda de algún tipo de información retrospectiva que permita decidir de forma aproximada sobre el patrón de conducta en la fase A.
Evidentemente, la técnica aquí analizada se trata de un caso extremo, pues es inusual disponer de una sola medición en la fase A. En ámbitos de investigación básica es improbable obtener un solo dato para la fase de línea base, además de poco pertinente optar por un diseño A-B, máxime cuando estas estrategias no son las más adecuadas para determinar el efecto de las intervenciones. Unicamente en aquellos casos de la investigación aplicada donde es recomendable una intervención rápida (pensemos en conductas con consecuencias lesivas para el individuo, por ejemplo), no existencia de registros previos e imposibilidad de realizar múltiples mediciones válidas (como la evaluación de intervenciones psicológicas realizadas sobre individuos con comportamiento antisocial sometidos, mediante mandato judicial, a regímenes de custodia abierta) o, cuando, por otros motivos, el investigador no pueda disponer de más información, podría considerarse analizar los datos mediante la estrategia aquí expuesta.
El punto más destacable en favor de esta estrategia analítica reside en su forma de evaluar la incidencia del tratamiento, pues no se centra en los cambios de nivel, como es habitual en la mayoría de las técnicas aplicadas al análisis de datos procedentes de diseños conductuales. Aunque tampoco es una alternativa a estas técnicas, sí es un complemento, pues el efecto del tratamiento pudiera no producir un cambio de nivel y, por contra, generar unos patrones de estructura interna en la serie de datos. También es cierto que la técnica tal como se ha presentado, en esta versión extrema, únicamente detecta estructuras en las cuales, para dos datos adyacentes, domina el crecimiento o decrecimiento; pero no es posible detectar estructuras de cambio caracterizadas, por ejemplo, por un incremento o decremento en forma de sierra, ni, obviamente, estructuras más complejas en las series. Estos problemas y la generalización a diseños A-B con varios datos en la fase A, además de su extensión a diseños A-B-A, entre otros, han sido recientemente estudiados (Solanas y Sierra, 1993); pero, en base a los resultados del presente trabajo, el análisis de incrementos-decrementos parece poco adecuado en el ámbito de la investigación psicológica, excepto que sea posible suponer inexistencia de dependencia serial.
A modo de síntesis, ¿qué puede decirse sobre la robustez de la técnica? Si nos referimos al efecto de la dependencia serial, puede considerarse una técnica robusta, al menos en el sentido tradicional de relativa insensibilidad ante leves violaciones de los supuestos (Huber, 1981). En un rango de valores del componente autorregresivo cercanos a la independencia, no hemos hallado una alteración significativa de la tasa empírica de error tipo I; pero, considerando el ámbito en el cual se utilizaría esta estrategia, donde los niveles de dependencia serial pueden ser elevados, parece aconsejable referirnos a una robustez débil. La expresión anterior es un intento de reflejar que, aunque la técnica es robusta, quizá no lo suficiente, en general, para analizar datos procedentes de diseños conductuales. Por otra parte, la asimetría del término error sí incide de forma severa, careciendo la técnica de robustez frente a la violación de este supuesto.
Los autores desean agradecer los comentarios y sugerencias realizadas por los revisores del manuscrito.
Notas
(1) Trabajo realizado con la ayuda de una beca predoctoral de formación de profesorado en áreas deficitarias, otorgada por el Departament d'Ensenyament de la Generalitat de Catalunya a Vicenta Sierra.
Referencias
Ballard, K.D. (1983). The visual analysis of time series data: Issues affecting the assessment of behavioral interventions. New Zeland Journal, 12, 69-73.
Crosbie, J. (1986). The inability of t Test to control Type I error with typical applied behavioral data. Manuscrito no publicado.
Crosbie, J. (1987). The stability of the binomial test to control Type I error with single-subject data. Behavioral Assessment, 9, 141-150.
Crosbie, J. (1989). The inappropriateness of the C statistic for assessing stability or treatment effects with single-subject data. Behavioral Assessment, 11, 315-325.
Edgington, E.S. (1967). Statistical inference N = 1 experiments. The Journal of Psvchology, 65, 195-199.
Edgington, E.S. (1980a). Random assignment and statistical test for one-subject experiments. Behavioral Assessment, 2, 19-28.
Edgington, E.S. (1980b). Randomization test. New York: Marcel Dekker.
Greenwood, K.M. & Mayas, T.A. (1990). Problems with application of interrupted time series analysis for brief single-subject data. Behavioral Assessment, 12, 355-370.
Huber, P.J. (1981). Robust statistics. John Wiluy & Sons: New York.
Jones, R.R.; Weinrott, M.R. & Vaught, R.S. (1978). Effects of serial dependency between visual and statistical inference. Journal of Applied Behavior Analysis, 11, 277-283.
Moore, G.H. & Wallis, W.A. (1943). Time series significance test based on signs of differences. Journal of the American Statistical Association, 38, 153-164.
Revusky, S.H. (1967). Some statistical treatments compatible with individual organism methodology. Journal of Experimental Analysis of Behavior,19, 319-330.
Solanas, A.; Salafranca, Ll. y Guardia, J. (1992). Análisis estadístico βn de diseños conductuales: Estadístico. Psicothema, 1, 253-259.
Solanas, A. y Sierra, V. (1993). Estadístico βn de k-ésirno orden en diseños conductuales A-B. Comunicación presentada en el III Simposium de Metodología de las Ciencias Sociales y del Comportamiento. Santiago de Compostela.
White, O.R. (1974). The «split middle»: a «quickie» method for trend estimation. Experimental Education Unit, Child Development and Mental Retardation Center, University of Washington.
Aceptado el 16 de mayo de 1994