Psicothema was founded in Asturias (northern Spain) in 1989, and is published jointly by the Psychology Faculty of the University of Oviedo and the Psychological Association of the Principality of Asturias (Colegio Oficial de Psicología del Principado de Asturias).
We currently publish four issues per year, which accounts for some 100 articles annually. We admit work from both the basic and applied research fields, and from all areas of Psychology, all manuscripts being anonymously reviewed prior to publication.
Psicothema, 1998. Vol. Vol. 10 (nº 3). 685-696
Juana Gómez Benito y María José Navas Ara*
Universidad de Barcelona, * Universidad Nacional de Educación a Distancia
Los tests estandarizados reflejan diferencias entre grupos que conviene discernir si son reales o producto del propio instrumento de medida. La investigación psicométrica de las últimas décadas ha abordado esta problemática con un desarrollo creciente de estudios de funcionamiento diferencial de los ítems para sujetos o grupos con el mismo grado de habilidad. Este trabajo analiza la posible existencia de diferencias reales (impacto) respecto al género en una prueba de aptitud numérica y el posible funcionamiento diferencial de sus ítems (FDI) mediante dos aproximaciones derivadas de la teoría de respuesta al ítem y un procedimiento factorial de tipo confirmatorio. Los resultados obtenidos sugieren una atenta revisión del contenido de varios ítems de la prueba. Una valoración del grado de concordancia entre las técnicas utilizadas aconseja la utilización de procedimientos de purificación iterativa en la aproximación factorial y apoya la utilización de evidencias múltiples concordantes para la toma de decisiones en estudios empíricos.
Gender-related impact and differential item functioning in a test of numerical ability. Standardized tests reflect differences between groups, and we should distinguish whether they are real or a product of the measuring instrument itself. In the last few decades psychometric research has approached this problem with the growing development of the studies of the differential item functioning for subjects or groups with the same degree of ability. This study examines the possible existence of real differences (impact) according to gender in a test of numerical ability and the possible differential item functioning (DIF), with two different procedures. The first is based on item response theory and the second on confirmatory factor analysis. Results suggest a careful review of the content of several items of the test. An examination of the convergence of results obtained with the different procedures supports the use of iterative purification mechanisms when working with confirmatory factor analytic techniques and the use of multiple convergent evidences in taking decisions in empirical studies.
El estudio sobre el posible sesgo de los ítems de un test hacia determinados grupos de población surge al final de la década de los 60 y tiene un desarrollo que bien podría calificarse de vertiginoso en las siguientes décadas, por razones obvias de carácter tanto social como político, así como por las profundas implicaciones psicológicas y educativas que éste tiene.
El análisis del posible sesgo de un test o de parte de sus ítems es parte sustancial del análisis de la validez del instrumento de medida en cuestión. Si algunos ítems del test no dependen únicamente del nivel del sujeto en el constructo medido –que es la finalidad única para la que se ha construido dicho test– sino que están influenciados también por la pertenencia de dicho sujeto a un determinado grupo social, cultural, étnico, etc., puede considerarse que estos ítems no son válidos para medir con equidad a sujetos que pertenecen a grupos distintos. En esta línea, Camilli y Shepard (1994) definen el sesgo de un test como invalidez o error sistemático del test al medir a los miembros de un determinado grupo.
Los ítems sesgados crean una distorsión en los resultados del test para los miembros de un grupo particular, de tal modo que sujetos que pertenecen a grupos distintos, aun teniendo el mismo nivel en el constructo medido, obtienen puntuaciones diferentes en dichos ítems; ello no se debe a un error aleatorio de medida sino a un error sistemático del instrumento de medida por el que un subgrupo de la muestra resulta beneficiado y otro perjudicado al evaluarles con los ítems en cuestión.
Evidentemente, no todas las diferencias entre grupos son atribuibles al sesgo, sino que éstas pueden ser perfectamente legítimas, esto es, pueden reflejar distinto nivel en el rasgo medido, en cuyo caso debe hablarse de impacto. Ackerman (1992) define el impacto como una diferencia entre grupos en el desempeño en un ítem causada por una diferencia real en la variable medida, mientras que el sesgo se relaciona con diferencias causadas por fuentes sistemáticas de variación ajenas al constructo que mide el test. Por ello, el propósito principal de un estudio de sesgo es discernir cuándo las diferencias de grupo son debidas a impacto –reflejan diferencias existentes entre los grupos en habilidad, conocimiento o experiencia– o a sesgo –reflejan diferencias artifactuales originadas en el proceso de medida en sí. En definitiva, lo fundamental es determinar si la causa por la que los grupos puntúan diferente en un ítem es relevante o irrelevante al constructo medido, ya que en el primer caso se tratará de impacto y en el segundo de sesgo.
Como apuntan Reynolds y Kamphaus (1990), la acepción sesgo tiene distintas connotaciones para diferentes audiencias, por lo que resulta ciertamente problemática. Así, desde el punto de vista legal, el término sesgo denota una práctica discriminatoria ilegal mientras que para el lego denota simplemente prejuicios; desde un punto de vista estadístico, el sesgo hace referencia a error sistemático en la estimación de un valor y, desde la perspectiva de la investigación psicométrica, este error sistemático ocurre en la determinación de la puntuación de un sujeto en un test como resultado de su pertenencia a un determinado grupo. Parece conveniente pues sustituir este término por otro semánticamente más neutral y que refleje de forma más precisa lo que se entiende técnicamente por sesgo (Fidalgo, 1996).
Aunque el acuerdo no es unánime, sí existe un consenso bastante generalizado entre los autores que investigan estas cuestiones en reservar el término funcionamiento diferencial del ítem (FDI) para el análisis estadístico de la cuestión y el término sesgo para las inferencias sobre la naturaleza de las diferencias observadas (Scheuneman, 1982; Scheuneman y Bleistein, 1989). Dicho de otro modo, el sesgo implica FDI y aspectos cualitativos de los ítems del test (Camilli, 1992); esto es, sólo se puede hablar de sesgo cuando sea posible relacionar el FDI con el constructo que se pretende medir.
Se entenderá que un ítem presenta FDI cuando sujetos que tienen el mismo nivel en la variable que se pretende medir obtienen puntuaciones distintas en dicho ítem, según pertenezcan a uno u otro grupo.
Encontrar explicaciones sustantivas a las diferencias relativas entre grupos es una cuestión ardua que pocos investigadores han abordado (véase Scheuneman, 1987; Skaggs y Lissitz, 1992) por lo que la inmensa mayoría de los estudios versan estrictamente sobre FDI. En particular, una buena parte de la investigación psicométrica de los últimos años ha versado sobre el desarrollo de técnicas de detección de FDI. Se han diseñado numerosos procedimientos basados principalmente en tablas de contingencia y en la teoría de respuesta al ítem (TRI) y recientemente ha empezado a utilizarse también el análisis factorial confirmatorio (AFC) (Navas y Gómez, 1994; Oort, 1992). En cuanto al contenido, los estudios se han centrado mayoritariamente en las variables etnia y género, aunque también comprenden una extensa gama de variables de tipo educativo, lingüístico y cultural.
En esta línea se inscribe el presente trabajo en el que, con datos reales y con una prueba comercializada muy utilizada en la práctica profesional, se plantea la hipótesis de diferencias según género en la aptitud numérica. Las investigaciones sobre esta temática (Halpern, 1986; Hedges y Nowell, 1995; Hyde, Fennema y Lamon, 1990; Keeves, 1988) han coincidido en detectar, en mayor o menor grado, un rendimiento más elevado en los varones. Ante ello se pretende comprobar en qué grado, en los datos concretos de este estudio, se confirma la existencia de estas diferencias en el binomio género-aptitud numérica y, en el caso de obtenerse, se tratará de dilucidar si se trata de diferencias reales en la aptitud numérica de varones y mujeres (impacto) o, por el contrario, esas diferencias se deben a deficiencias en los ítems de la prueba utilizada para medir esa aptitud. Para ello, se propone utilizar distintas estrategias de detección, basadas en la TRI y en el AFC.
Método
Recogida de datos
Los datos se han obtenido de una muestra de 8738 alumnos –4913 varones y 3825 mujeres– de segundo curso de Enseñanzas Medias a los que se les ha aplicado el Factor Numérico de la batería TEA en su nivel 3 (a partir de ahora FNTEA) que mide la aptitud numérica a través de una serie de ejercicios de cálculo que implican operaciones algebraicas básicas con enteros, decimales, fracciones, cálculo de porcentajes, etc.. La prueba completa consta de 30 ítems de elección múltiple, con cinco alternativas de respuesta cada uno; en este trabajo se han utilizado únicamente los 23 ítems que en un estudio previo (Navas, 1994) cumplieron el supuesto de unidimensionalidad.
Evaluación del impacto
El posible impacto de la prueba FNTEA con respecto al género se ha evaluado mediante un contraste de hipótesis acerca de la igualdad o desigualdad de la proporción de respuestas correctas obtenidas en cada ítem por la muestra de varones y mujeres (Ironson, 1982; Linn y Harnisch, 1981) calculando el siguiente estadístico de contraste:
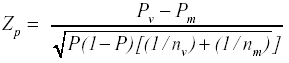
donde
Pv: proporción de respuestas correctas al ítem en la muestra de varones.
Pm: proporción de respuestas correctas al ítem en la muestra de mujeres.
P: proporción de respuestas correctas en el total de la muestra con valor igual a:
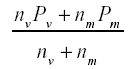
nv: número de sujetos en la muestra de varones.
nm: número de sujetos en la muestra de mujeres.
Detección de FDI
Se ha analizado el FDI de la prueba FNTEA con respecto al género utilizando dos procedimientos basados en la TRI y un procedimiento basado en el AFC.
Aproximación basada en la TRI
El estudio del FDI desde la perspectiva de la TRI ha seguido tradicionalmente dos enfoques distintos aunque, en cierta medida, complementarios: (1) cálculo o estimación del área existente entre las Curvas Características de los Ítems (CCI) estimadas en los grupos de interés (Hambleton y Rogers, 1989; Kim y Cohen, 1991; Linn, Levine, Hastings y Wardrop, 1981; Raju, 1988, 1990; Rogers y Hambleton, 1989; Rudner, 1977) y (2) contraste de hipótesis acerca de la igualdad de los parámetros que caracterizan a las CCIs estimadas en dichos grupos (Hulin, Drasgow y Komocar, 1982; Lord, 1977, 1980; Mellenbergh, 1972, 1989; Wright, Mead y Draba, 1976).
En línea con el primer enfoque, en el presente trabajo se ha examinado de FDI mediante el índice SC1 (Suma de Cuadrados 1), tal como es definido por Shepard, Camilli y Williams (1984):
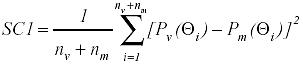
donde
Pv(Θi): probabilidad de observar una respuesta correcta al ítem en la muestra de varones, supuesto un nivel de habilidad para el sujeto de Θi.
Pm( Θi ): probabilidad de observar una respuesta correcta al ítem en la muestra de mujeres, supuesto un nivel de habilidad para el sujeto de Θi.
Para poder calcular el índice anterior es necesario equiparar previamente las estimaciones obtenidas para los parámetros de ítems y sujetos en las muestras de varones y mujeres. Estas se obtuvieron con el programa RASCAL (Assessment System Corporation, 1995 ). El método elegido para poner en la misma escala las estimaciones obtenidas en ambas muestras ha sido el método estándar de la media y la desviación típica (Warm, 1978).
Con el fin de interpretar los resultados obtenidos al calcular el índice SC1 para cada ítem de la prueba FNTEA, se decidió determinar un valor a partir del cual se consideraría que un ítem presenta FDI con respecto al género. El procedimiento para determinar ese valor puede ser descrito brevemente como sigue: Se dividió aleatoriamente la muestra de varones en dos grupos; una primera submuestra estaba formada por los sujetos con número de orden par dentro de la muestra y una segunda submuestra por los sujetos con número de orden impar. Se calculó el SC1 considerando estas dos submuestras. Dado que todos los sujetos de ambas submuestras eran varones, la distribución de frecuencias así obtenida para el índice SC1 proporcionaría una línea base que podría servir de referencia para interpretar de forma significativa los valores obtenidos al calcular SC1 en la muestra de varones y mujeres. Se repitió todo el proceso anterior en la muestra de mujeres y se decidió que un posible punto de corte a partir del cual marcar un ítem para una revisión en profundidad en relación a posibles problemas de FDI podría ser el valor más alto obtenido para SC1 en las submuestras de varones y en las de mujeres.
En línea con el segundo enfoque señalado dentro de la TRI, en el presente trabajo se ha calculado un estadístico de contraste inicialmente propuesto por Fischer (1974) – Zb – que se distribuye normalmente y somete a prueba la hipótesis de igualdad del parámetro de dificultad del modelo de Rasch en las muestras de varones y mujeres:
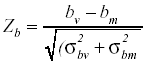
donde
bv : valor estimado para el parámetro de dificultad del ítem en la muestra de varones
bm : valor estimado para el parámetro de dificultad del ítem en la muestra de mujeres
σ2bv : varianza error del estimador del parámetro de dificultad del ítem en la muestra de varones
σ2bm : varianza error del estimador del parámetro de dificultad del ítem en la muestra de mujeres.
El paso previo antes de calcular cualquiera de estos dos estadísticos es comprobar que los datos empíricos obtenidos al aplicar la prueba FNTEA a una muestra de varones y de mujeres se ajustan razonablemente bien a un modelo de la TRI. Para dilucidar esta cuestión, se examinaron los supuestos del: a) unidimensionalidad, mediante el test del autovalor y el test de la línea base aleatoria, b) ausencia de aciertos al azar, mediante el estudio de la actuación de los sujetos con puntuaciones más bajas en el test en los ítems más difíciles, y c) discriminación constante, mediante el estudio de la distribución de frecuencias de la correlación biserial puntual entre las puntuaciones de cada ítem y la puntuación total del test. Los resultados obtenidos tras estos análisis (véase Navas, 1994, para un tratamiento en detalle) permiten afirmar que los datos se ajustan satisfactoriamente al modelo logístico de un parámetro.
Aproximación basada en el AFC
El FDI de la prueba FNTEA se ha evaluado también mediante AFC utilizando el programa LISREL 8 (Jöreskog y Sörbom, 1993a). Dicho procedimiento permite introducir la posible causa de FDI como un factor de análisis adicional al constructo que mide la prueba y contrastar un modelo nulo en el que se fijan a cero las saturaciones de los ítems en este factor (Oort, 1992).
La especificación de dicho modelo nulo representa un modelo sin FDI, en el que los ítems saturan únicamente en las variables latentes que mide el test. La contrastación de FDI del ítem i con respecto a un determinado factor k se lleva a cabo mediante la comparación del modelo nulo con otro modelo alternativo en el que la saturación de ese ítem i en el factor k se deja libre; si dicho modelo alternativo ajusta significativamente mejor que el modelo nulo, se considerará que el ítem i presenta FDI con respecto al factor k.
En vez de realizar tantas comparaciones de modelos como ítems hay en el test, pueden utilizarse los Indices de Modificación (IM) de cada ítem en la estimación del modelo nulo. Los valores de los IM muestran cuanto aumentará el ajuste del modelo si la saturación del ítem i en la causa de FDI k se deja libre; por lo tanto, cada IM significativo es muestra de FDI en el ítem respectivo ya que indica que aquel ítem depende, además de la variable rasgo que mide la prueba, de la variable de FDI analizada.
Para comprobar la dirección del FDI de los ítems con IM significativo, pueden utilizarse los valores del Cambio Esperado en el Parámetro (CEP) que proporciona el programa Lisrel. Si, de acuerdo con un IM significativo, el ítem i presenta FDI con respecto al factor k y el CEP para la regresión de este ítem i en k es positivo, significa que el ítem i es más fácil o más atractivo para los sujetos con alta puntuación en el factor de FDI k y viceversa. Es decir, sujetos con igual cantidad de rasgo T puntuarán más alto en el ítem i cuando tengan más cantidad de k y viceversa.
Los parámetros se han estimado mediante el procedimiento de mínimos cuadrados totalmente ponderados (WLS), tal como recomienda Jöreskog (1990) para datos dicotomizados, habiendo calculado previamente la matriz de correlaciones policóricas y su correspondiente matriz de variancias y covariancias asintóticas mediante Prelis 2 (Jöreskog y Sörbom, 1993b).
Resultados
Evaluación del impacto
La primera columna de la tabla 1 recoge los valores obtenidos para el estadístico de contraste que sometía a prueba la hipótesis de igualdad de proporciones de respuestas correctas en el grupo de varones y de mujeres. Dado que la distribución muestral de este estadístico es normal N(0,1), cualquier valor superior a |2| indicará que estamos frente a un ítem en el que se detecta la presencia de impacto con respecto a la variable considerada; no obstante, un valor más apropiado para marcar un ítem como susceptible de mostrar impacto sería |3|, ya que el tamaño muestral de los dos grupos de interés es bastante elevado (en torno a los 4.000 sujetos por grupo). Como puede observarse en dicha columna, sólo 5 de los 23 ítems examinados presentan valores inferiores a |3| (ítems 1-3, 5 y 19); en estos 5 ítems la actuación de los sujetos de ambos grupos no difiere significativamente, mientras que los restantes 18 ítems evidencian impacto en el sentido de que el grupo de varones muestra una actuación significativamente mejor que el grupo de mujeres.
Detección de FDI
Aproximación basada en la TRI
La segunda columna de la tabla 1 recoge el valor obtenido para el índice SC1 cuando éste se calcula en los dos grupos de interés –varones y mujeres– y las columnas tercera y cuarta cuando se calcula en las submuestras de varones y de mujeres, respectivamente. El valor más alto observado en las columnas tercera y cuarta es 0.00126516 (ítem 15 en submuestra de mujeres). Si se examina ahora la segunda columna, se observa que hay 12 ítems con valores inferiores (ítems 1, 4, 7-12, 14, 15, 19 y 20). Por tanto, estos resultados apuntan a la posible existencia de FDI en los restantes 11 ítems de la prueba FNTEA.
La última columna de la tabla 1 recoge los valores obtenidos para el estadístico de contraste que sometía a prueba la hipótesis de igualdad del parámetro de dificultad del ítem obtenido en el grupo de varones y de mujeres. La distribución muestral de este estadístico también es N(0,1). Si se examinan los valores de esta última columna, se observa que hay 11 ítems que no superan el valor |3| (ítems 4, 7-12, 14, 15, 19 y 20), por lo que los otros 12 ítems de la prueba FNTEA parecen presentar posibles problemas de FDI.
Aproximación basada en el AFC
Para determinar si la variable género tiene o no una influencia significativa en cada uno de los ítems de la prueba FNTEA mediante AFC, se introduce en el análisis la variable género como único indicador de un posible factor de FDI y se contrasta el modelo nulo en el que se han fijado a cero las saturaciones de los ítems en dicho factor.
En la tabla 2 se expresan los resultados más relevantes de la estimación del modelo nulo. La primera columna muestra la significación de las saturaciones de los respectivos ítems en el primer factor, que especifica el rasgo medido por la prueba. De su elevada significación se extrae que los 23 ítems incluídos en el análisis son buenos indicadores del factor numérico que pretende medir FNTEA.
La segunda columna de la tabla 2 expresa los valores obtenidos por los ítems en los IM del segundo factor que especifica, en este caso, el género. Trece de los 23 ítems analizados no muestran IM significativos (ítems 1, 3, 4, 7, 10, 12, 15-17, 20-23). Los restantes ítems son sospechosos de FDI ya que dependerían, no sólo del factor numérico, sino también de la variable género; la significación de sus respectivos IM denota que el ajuste del modelo aumentaría si la saturación del ítem respectivo en el segundo factor se deja libre. En la tercera columna figuran los valores de los CEP de cada ítem de la prueba que representan una estimación del cambio esperado en el valor del respectivo parámetro fijado cuando se añade al modelo nulo como un parámetro libre.
En función de estos resultados, se reespecifica un modelo alternativo en el que se liberan las saturaciones en el segundo factor de aquellos ítems con IM significativo en el modelo nulo. La tabla 3 muestra las estimaciones de la matriz factorial de este modelo alternativo, con sus correspondientes valores T entre paréntesis. La comparación de la primera columna de las tablas 2 y 3 pone en evidencia que la significación de las saturaciones de los ítems en el primer factor son prácticamente idénticas, lo que constata su estabilidad. En la segunda columna de la tabla 3 figuran los valores obtenidos por las saturaciones de los ítems formulados como libres en el factor género; en general siguen las expectativas de cambio previstas en la tercera columna de la tabla 2 excepto en el ítem 8 cuyo valor T no alcanza la significación en el factor género, por lo que su correspondiente saturación debería fijarse a cero de nuevo.
Como los parámetros libres del modelo nulo representan un subconjunto de los parámetros libres del modelo alternativo, el primer modelo puede considerarse anidado en el segundo, por lo que es posible comparar su respectivo ajuste mediante la diferencia de las χ2 de ambos modelos; dicha diferencia es altamente significativa (p<.001), por lo que el modelo alternativo constituye una mejor representación de la realidad que el modelo sin FDI.
Convergencia en los resultados
Los resultados obtenidos por ambas aproximaciones en la detección del FDI en la prueba FNTEA no coinciden exactamente y, al trabajar con datos reales no se pueden extraer conclusiones precisas sobre la respectiva capacidad de detección de cada procedimiento, aunque sí es posible una valoración basada en el grado de coincidencia mostrado entre las distintas técnicas. Para ello, se ha utilizado el estadístico Kappa (Cohen, 1960) que se define como la proporción de concordancias observadas corregida por la de concordancias aleatorias.
Son particularmente altos los valores de concordancia obtenidos entre los dos métodos basados en la TRI (k = 91.20) lo que indicaría que es prácticamente indiferente cuál de ellos se selecciona en un estudio de FDI. Sin embargo, la coincidencia entre los resultados obtenidos por el AFC y los dos procedimientos basados en la TRI es prácticamente nula (k = 3.82 y 3.75, respectivamente).
La selección de los ítems con FDI se ha llevado a cabo utilizando como criterio la puntuación total del test, que está formada tanto por ítems sin FDI como con FDI. Oort (1992) propone un procedimiento iterativo de purificación en el que el criterio se redefine en sucesivas etapas como la puntuación de todos los ítems en el test excepto aquel que muestra un mayor grado de FDI en la etapa anterior, de tal modo que en la última etapa ningún ítem con FDI forma parte del criterio. Ante la falta de convergencia observada por los resultados obtenidos con las dos aproximaciones, es planteable si un procedimiento de purificación del análisis del FDI mediante AFC obtendría resultados más próximos a los conseguidos por las técnicas basadas en la TRI.
Los resultados de este procedimiento iterativo se muestran en la tabla 4. La primera columna indica el número de ítems que forman la medida del criterio en cada una de las sucesivas etapas. En la segunda columna figura el ítem que debe eliminarse en la próxima etapa en función de los valores IM y CEP obtenidos por dicho ítem que figuran, respectivamente, en las dos últimas columnas. El criterio finalmente purificado consta de 10 ítems (1, 4, 7, 8, 10, 12, 14, 15, 20 y 21) que funcionan de modo equivalente en los dos grupos comparados, ya que los ítems con FDI han sido eliminados paulatinamente en las sucesivas etapas.
El índice de concordancia alcanzado entre los resultados del AFC con purificación y de los dos procedimientos basados en la TRI es de 65.41 y 56.35, respectivamente, lo que equivale a un nivel medio, considerado satisfactorio por Cohen.
Conclusiones
En primer lugar, en la prueba FNTEA se ha detectado una mayor habilidad numérica en los sujetos varones en gran parte de sus ítems (4, 6-18 y 20-23), lo que hace aumentar ligeramente su puntuación media en la prueba global. Conviene interpretar con precaución los resultados obtenidos en este estudio de impacto, dado el elevado tamaño muestral con el que se ha trabajado y la sensibilidad al mismo de la prueba utilizada; sin embargo, hay que constatar su coincidencia con los datos aportados por el meta-análisis llevado a cabo por Hyde et al. (1990) sobre 100 estudios de diferencias de género en rendimiento de matemáticas, y por el análisis secundario realizado por Hedges y Nowell (1995) que encuentran tamaños del efecto favorables a los sujetos varones, aunque de pequeña magnitud.
En segundo lugar, este estudio pone de manifiesto que las diferencias encontradas entre los sujetos varones y mujeres se pueden deber, en algunos ítems, a deficiencias de los mismos y no tanto a diferencias reales en la aptitud numérica.
En tercer lugar, este estudio evidencia la debilidad de la utilización de un único método en estudios aplicados de detección de ítems con FDI y apoya el uso de evidencias múltiples concordantes para la toma de decisiones en estudios empíricos. En efecto, la identificación de los ítems con FDI de la prueba FNTEA no es totalmente coincidente entre los diferentes métodos utilizados. Ante los resultados obtenidos podría proponerse la revisión de los ítems 2, 5, 6, 13 y 18 que son detectados por todos los procedimientos utilizados y un atento análisis de contenido de los ítems 3, 16, 17, 22 y 23 que son detectados conjuntamente por los procedimientos basados en la TRI y el AFC con purificación.
Por último, los resultados de este trabajo también evidencian que la aproximación factorial mediante modelos de ecuaciones estructurales es un procedimiento eficaz para detectar el FDI de los ítems de un test, frente a las inconsistencias detectadas al utilizar la aproximación factorial exploratoria (Navas, 1994); ahora bien, la comparación entre los resultados de concordancia conseguidos por los dos procedimientos de detección de FDI basados en el AFC (sin y con purificación) remarca que es preciso pulir el procedimiento factorial confirmatorio mediante la purificación paso a paso del criterio que va eliminando paulatinamente los ítems con FDI, como ya se puso de manifiesto en el estudio de Navas y Gómez (1994) con datos simulados. Por ello cabe desaconsejar la utilización del procedimiento de AFC sin purificación para decidir qué ítems deben revisarse por sospecha de FDI ya que es remarcable la falta de coincidencia de este método con los basados en la TRI, tanto en la detección de los ítems con FDI como en la identificación de aquéllos que no lo presentan.
Discusión
Los tests psicológicos y educativos forman parte fundamental de procesos de evaluación que implican toma de decisiones y que establecen diferencias entre grupos. Si los ítems de un test presentan problemas de FDI, las puntuaciones para grupos distintos no son comparables y, por lo tanto, éstos no reciben un tratamiento equitativo. La posible falta de imparcialidad de los instrumentos de medida ha ocasionado que los estudios de FDI se hayan convertido en parte integral del procedimiento de construcción de nuevos tests y de reevaluaciones de pruebas existentes; es en extremo conveniente someter a los instrumentos de medida a este proceso de refinamiento conducente a la identificación de subconjuntos de ítems sin sesgo que permitan comparaciones válidas entre grupos.
Una vez establecida de forma inequívoca la existencia de ítems que presentan un funcionamiento diferencial respecto a un grupo, el paso siguiente a dar por el constructor (o el usuario) del test es tratar de plantearse sus posibles causas o explicaciones probables. Habitualmente, esto supone pasar del terreno del FDI al del sesgo, aunque esto no siempre es así.
En efecto, en muchos casos de ítems con FDI el término sesgo no describe de forma precisa la situación (Holland y Thayer, 1988). La observación de FDI entre algunos ítems de un test no implica necesariamente que exista sesgo en los ítems; ésta es, desde luego, una posibilidad pero otra es que, por ejemplo, el FDI obedezca a que se trabaja con tamaños muestrales normalmente distintos (y desequilibrados) en los grupos focal y de referencia, por lo que se pueden obtener estimaciones menos precisas en el grupo con menor tamaño muestral. En este caso, las diferencias observadas en la actuación en un ítem en los sujetos de distintos grupos se pueden deber a la diferente precisión con la que se han estimado los parámetros en uno y otro grupo y no a una validez diferencial de la prueba para los distintos grupos.
Sin embargo, lo más habitual es que la pertenencia a un grupo determinado puede enmascarar variables de gran significación para el constructo pretendidamente evaluado (Shyer, 1993). Como apuntan certeramente Lautenschlager y Park (1988), 'la indicación estadística de sesgo del ítem debe de ir acompañada por el examen del contexto y del contenido del ítem (o incluso de las características de la muestra) para determinar si es justificable la identificación de un ítem como sesgado' (p.375). En suma, es menester buscar aquellas características del ítem que interactúan con la pertenencia al grupo para poder reducir el posible sesgo (Linn, Levine, Hastings y Wardrop, 1981).
En esta línea, los ítems que se han detectado como afectos de FDI deben ser examinados por expertos, por una parte, en currículum académico y, por otra, en psicología diferencial especializada en diferencias de género para conjuntamente establecer las causas por las que dichos ítems han funcionado de forma distinta entre ambos géneros y determinar si realmente están midiendo lo mismo en los dos grupos.
Por último, hay que señalar que el hecho de que un ítem presente FDI no conlleva directamente su eliminación del test: para ello, hay que determinar si la fuente de dificultad diferencial es relevante o no. Sólo se puede etiquetar a un ítem de sesgado en el marco de un análisis lógico que identifique claramente el constructo de interés, sugiera la presencia de otro constructo secundario contenido en ese ítem en particular y lo juzgue irrelevante al constructo principal ya que lo único que ocasiona es una distorsión en su medida. Por ejemplo, una palabra que presenta una dificultad diferencial para dos grupos de sujetos debería de ser eliminada de un ítem en una prueba que mida aptitud numérica, pero no de una diseñada para evaluar el nivel de vocabulario.
En definitiva, los resultados de este estudio y su posible repercusión en la toma de decisiones sobre un test determinado proporcionan un ejemplo de la necesidad de evidencia múltiple convergente y muestran la conveniencia de la utilización de análisis de este tipo en la investigación del FDI de instrumentos de medida en fase de elaboración o de revisión; además, queda patente la necesidad de buscar explicaciones substantivas de las causas del FDI para poder extraer conclusiones sobre el sesgo de los ítems, encuadrándose éstas en el amplio marco del estudio de la validez del test. Como afirman Millsap y Everson (1993), ‘la existencia de sesgo en una medida dada indica que no se acaba de comprender del todo el constructo que se está evaluando. Por tanto, los estudios de sesgo en la medida deberían de ser promovidos como parte del proceso general de la validez de constructo’ (p. 329).
Ackerman, T.A. (1992). A didactic explanation of item bias, item impact, and item validity from a multidimensional perspective. Journal of Educational Measurement, 29, 67-91.
Assessment Systems Corporation (1995). RASCAL for Windows (Version 3.50e). St. Paul, MN: Author.
Camilli, G. (1992). A conceptual analysis of differential item functioning in terms of a multidimensional item response model. Applied Psychological Measurement, 16(2), 129-147.
Camilli, G. y Shepard, L.A. (1994). Methods for Identifying Biased Test Items. Newbury Park, C.A.: Sage.
Cohen, J. (1960). A coefficient of agreement for nominal scales. Educational and Psychological Measurement, 20, 37-46.
Fidalgo, A.M. (1996). Funcionamiento diferencial de los ítems. En J. Muñiz (Coord.), Psicometría. Madrid: Universitas.
Halpern, D.F. (1986). Sex Differences in Cognitive Abilities. Hillsdale, N.J.: Erlbaum.
Hambleton,R.K. y Rogers, J. (1989). Detecting Potentially Biased Test Items: Comparasion of IRT Area and Mantel-Haenszel Methods. Applied Measurement in Education, 2, 4, 313-334.
Hedges, L. y Nowell, A. (1995). Sex differences in mental test scores, variability, and numbers of high-scoring individuals. Science, 269, 41-45.
Holland, P.W. y Thayer, D.T. (1988). Differential item functioning and the Mantel-Haenszel procedure. En H.Wainer y H.I.Braun (Eds.) Test Validity, (pp.129-145). Hillsdale, NJ.:LEA.
Hulin,C.L.; Drasgow, F. y Komocar,J. (1982). Applications of Item Response Theory to Analysis of Attitude Scale Translations. Journal of Applied Psychology, 67, 818-825.
Hyde, J.S., Fennema, E. y Lamon, S.J. (1990). Gender differences in mathematics performance attitudes/affect: A meta-analysis. Psychological Bulletin, 107, 139-155.
Ironson,G.H. (1982). Use of Chi-Square and Latent-Trait Approaches for Detecting Item Bias. En R.A.Berk (Ed.), Handbook of Methods for Detecting Item Bias. Baltimore, MD: Johns Hopkins University Press.
Jöreskog, K.G. (1990). New developments in LISREL: Analysis of ordinal variables using polychoric correlations and weighted least squares. Quality and Quantity, 24, 387-404.
Jöreskog, K. G. y Sörbom, D. (1993a). LISREL 8. User's Reference Guide. Chicago, IL.: Scientific Software.
Jöreskog, K. G. y Sörbom, D. (1993b). PRELIS 2. User's Reference Guide. Chicago, IL.: Scientific Software.
Keeves, J.P. (1988). Sex differences in Ability and Achievement. En J.P. Keeves (Ed.), Educational Research, Methodology and Measurement: An International Handbook. Oxford: Pergamon Press.
Kim,S. y Cohen,A.S. (1991). A Comparasion of Two Area Measures for Detecting Differential Item Functioning. Applied Psychological Measurement, 15, 3, 269-278.
Lautenschlager, G. y Park, D. (1988). IRT item bias detection procedures: issues of model misspecification, robustness, and parameter linking. Applied Psychological Measurement, 12, 365-376.
Linn,R.L. y Harnisch,D.L. (1981). Interactions between Item Content and Group Membership on Achievement Test Items. Journal of Educational Measurement, 18, 109-118.
Linn,R.L.; Levine,M.V.; Hastings,C.N. y Wardrop,J.L. (1981). Item Bias in a Test of Reading Comprehension. Applied Psychological Measurement, 5, 159-173.
Lord,F.M. (1977). Practical Applications of Item Characteristic Curve Theory. Princeton, NJ: Educational Testing Service.
Lord,F.M. (1980). Applications of Item Response Theory to Practical Testing Problems. Hillsdale, NJ: LEA.
Mellenbergh,G.J. (1972). Applicability of the Rasch Model in Two Cultures. En L.J.C.Cronbach y P.J.D.Drenth (Eds.), Mental Tests and Cultural Adaptation. The Hague: Mouton.
Mellenbergh,G.J. (1989). Item Bias and Item Response Theory. International Journal of Education Research, 13, 2, 127-143.
Millsap, R.E. y Everson, H.T. (1993). Methodology review: Statistical approaches for assessing measurement bias. Applied Psychological Measurement, 17(4), 297-334.
Navas Ara, M. J. (1994). Utilización del Análisis Factorial y Medidas del Area como Métodos en la Detección de Sesgo. Psicothema, 6(3), 493-501.
Navas Ara, M. J. y Gómez Benito, J. (1994). Comparison of several bias detection techniques. Paper presented at the 23rd. International Congress of Applied Psychology, Madrid.
Oort, F. J. (1992). Using Restricted Factor Analysis to Detect Item Bias. Methodika, VI, 150-166.
Raju, N. S. (1988). The Area between Two Item Characteric Curves. Psychometrika, 53, 495-502.
Raju, N. S. (1990). Determining the Significance of Estimated Signed and Unsigned Areas between Two Item Response Functions. Applied Psychological Measurement, 14(2), 197-207.
Reynolds, C.R. y Kamphaus, R.W. (1990). Handbook of psychological and educacional assessment of children intelligence and achievement. New York: The Guilford Press.
Rogers,J. y Hambleton,R.K. (1989). Evaluation of Computer Simulated Baseline Statistics for Use in Item Bias Studies. Educational and Psychological Measurement, 49, 355-369.
Rudner,L.M. (1977). An Approach to Bias Item Identification Using Latent Trait Measurement Theory. Comunicación presentada en la reunión anual de la AERA, New York.
Scheuneman, J.D. (1982). A posteriori analyses of biased items. En R. Berk (Ed.), Handbook of methods for detecting test bias. Baltimore: Johns Hopkins University Press.
Scheuneman, J.D. (1987). An experimental, exploratory study of causes of bias in test items. Journal of Educational Measurement, 24, 97-118.
Scheuneman, J.D. y Bleistein, C.A. (1989). A consumer's guide to statistics for identifying differential item functioning. Applied Measurement in Education, 2, 255-275.
Shepard,L.A.; Camilli,G. y Williams,D.M. (1984). Accounting for Statistical Artifacts in Item Bias Research. Journal of Educational Statistics, 9, 93-128.
Skaggs, G. y Lissitz, R.W. (1992). The consistency of detecting item bias across of different test administration. Journal of Educational Measurement, 29, 227-242.
Warm,T. (1978). A Primer of Item Response Theory. US Coast Guard Institute Oklahoma City.
Wright,G.H.; Mead,R. y Draba,R. (1976). Detecting and Correcting Item Bias with a Logistic Response Model (Research Memorandum No.22). Chicago: University of Chicago. Statistical Laboratory. Department of Education.
Aceptado el 20 de febrero de 1998