Psicothema was founded in Asturias (northern Spain) in 1989, and is published jointly by the Psychology Faculty of the University of Oviedo and the Psychological Association of the Principality of Asturias (Colegio Oficial de Psicología del Principado de Asturias).
We currently publish four issues per year, which accounts for some 100 articles annually. We admit work from both the basic and applied research fields, and from all areas of Psychology, all manuscripts being anonymously reviewed prior to publication.
Psicothema, 1991. Vol. Vol. 3 (nº 2). 453-466
José María TOUS RAL* y Pere Joan FERRANDO PIERA**
Departamento de Personalidad, Evaluación y Tratamiento Psicológico. Universidad de Barcelona. **Departamento de Educación y Psicología, Facultad de Tarragona Universidad de Barcelona.
Se presenta una aplicación del escalamiento multidimensional ENID) no métrico al análisis del diferencial semántico propuesto por Osgood como medida del significado. El ENID se plantea como una alternativa a la representación configuracional y al análisis de coordenadas principales (ACP). En los tres casos se obtienen soluciones muy similares. Sin embargo, el EMD tiene sobre el ACP la ventaja de que no requiere una buena estructura métrica en la matriz de proximidades, por lo que, dadas las características de la escala de diferencial semántico, se presenta como una solución más apropiada y más generalizable.
Palabras Clave: ENID, Diferencial semántico.
ABSTRACT
Application of MDS for the analysis of differential semantic. We present here an application of non-metric multidimensional scaling (MM) for the analysis of semantic differential proposed by Osgood as a measure of meaning. MDS is presented as an alternative to configurational representation and analysis of principal co-ordinates (PCA). In the three cases very similar solutions were obtained. However, MDS has the advantage over PCA that it doesn' t require a positive semi-definite matriz. Threrefore, it is a more appropiate method for the characteristics of semantic differential.
Key Words: MDS. Differential semantic.
De acuerdo con Coombs (1964), la observación de una relación entre dos objetos puede categorizarse bien como una relación de orden (dominancia), bien como una relación de proximidad (consonancia). En ambos casos, las observaciones pueden distribuirse en una matriz que representa las relaciones dos a dos entre este conjunto de objetos.
El concepto de proximidad se considera como un índice definido entre pares de objetos que cuantifica, de algún modo, el grado en que estos objetos se parecen entre sí. Más específicamente, pueden distinguirse una serie de formas de medida dentro de este concepto general. Así, sea δij una medida de proximidad entre un par de objetos (i,j); si esta medida está escalada de tal forma que los valores más elevados de δij corresponden a los pares de estímulos más semejantes, diremos que es una medida de similitud. Si, por el contrario, los valores más altos de δij corresponden a los pares de estímulos menos semejantes, la definiremos como una medida de disimilitud. (Morlat, 1982).
El desarrollo de los métodos de análisis de matrices de proximidad sufrió un cambio cualitativo importante a partir de los años 50, cuando se introdujo la idea de interpretar los datos de proximidad como datos de distancia, basándose en una analogía propuesta inicialmente por Richardson (1938). Una medida de distancia puede considerarse como una medida de disimilitud (Davidson, 1983) y el paralelismo entre estos dos conceptos puede observarse a partir de una serie de axiomas. Más concretamente, una función d, definida entre pares de objetos (a,b) debe satisfacer cuatro axiomas para considerarse una disimilitud carente de error o de incoherencia (Morlat, 1982):
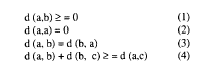
De acuerdo con las restricciones impuestas por un modelo euclidiano, podemos definir la función de relación entre disimilitud y distancia como:
![]()
donde a,b representan un par de objetos, n, representa las dimensiones del espacio euclidiano, y, xaj y xbj representan las proyecciones de a y b sobre la dimensión j.
El planteamiento inicial de Osgood, Suci y Tannembaum (1957) para abordar el problema de la medición del significado consiste en suponer un espacio semántico de dimensionalidad desconocida y de carácter euclidiano. Una escala semántica, definida por un par de adjetivos polares, se considera una función lineal que pasa por el origen de este espacio. Un conjunto de escalas definen un espacio multidimensional. Si las escalas son redundantes no añaden nuevas dimensiones a las ya existentes en este espacio, por lo que, siguiendo el principio de parsimonia, se exige que dicho espacio se defina a partir de un mínimo de ejes independientes entre sí.
Este requisito puede conseguirse mediante un análisis factorial de las escalas de adjetivos (independientemente del concepto que éstas pretendan medir). Mediante el análisis se obtienen una serie de combinaciones lineales independientes de las escalas originales y, a partir de aquí, pueden obtenerse las p tuaciones factoriales para los conceptos. Geométricamente, la puntuación de un concepto equivale a un punto que se proyecta sobre un sistema de n-coordenadas ortogonales (los factores). Considerando un vector desde el origen del sistema hasta dicho punto, Osgood, Suci y Tannembaum establecieron una relación de isomorfismo tal que el módulo del vector equivaldría a la intensidad del significado (entendida desde la teoría como evocación de respuestas mediacionales), mientras que la dirección sería identificable a la cualidad de dicho significado. (Osgood, Suci y Tannembaum, 1957).
En la práctica, la obtención de ejes independientes puede llevarse a cabo mediante diversos métodos más o menos complejos. Osgood, Suci y Tannembaum inicialmente utilizaron el método de factorización centroide seguido de una rotación quartimax. Mediante este método se obtuvieron tres factores: evaluación, potencia y actividad (Osgood, Suci y Tannembaum, 1957).
Puede observarse que la comparación de las puntuaciones correspondientes a diversos conceptos obtenidas en un conjunto de factores independientes es equivalente a un análisis de perfiles. En la representación geométrica el perfil corresponde a la columna de coordenadas del punto que define al concepto. Las medidas más habitualmente utilizadas en el análisis de perfiles son el coeficiente; de correlación producto - momento y la distancia euclidiana. Sin embargo, como señalan Fleiss y Zubin, (1969) en este tipo de análisis la correlación producto-momento como indicador tan sólo es sensible a la forma del perfil, mientras que la distancia euclidiana es sensible tanto a la forma como a la elevación por lo que se muestra como una mejor opción. Por esta razón, Osgood Suci y Tanembaum que, inicialmente, habían factorizado matrices de correlaciones cambiaron posteriormente de indicador y utilizaron la distancia euclidiana. Al cambiar el indicador, variaron, también el método de factorización pasando del centroide al método diagonal de Thurstone. Este método estaba inicialmente destinado al análisis de matrices de correlaciones, sin embargo resulta también aplicable a matrices de distancias y a matrices de productos cruzados.
En este punto podemos plantear de forma más específica el análisis en el que se basa el presente artículo. En principio, su modelo estructural sería el siguiente:
![]()
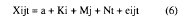
Donde una puntuación es obtenida a partir de una serie de i escalas (K), que se combinan en j factores independientes (M) y que se aplican a t sujetos (N).
En nuestro caso concreto estamos interesados en estudiar las distancias existentes entre una serie de 6 colores. Cada color tendrá un perfil consistente en el promedio de las puntuaciones de los t sujetos (100) en cada uno de los j factores independientes (4) cada uno de los cuales está formado por una combinación lineal (suma simple en este caso) de i escalas (12). La matriz inicial de nuestro análisis es la siguiente:
|
Conceptos Colores |
Antigüedad |
Solidez |
Seguridad |
Poder |
Σ |
X |
|
1. Ocre 2. Marrón 3. Granate 4. Azul 5. Gris 6. Naranja Σ X |
0,59* 0,92* 0,51* 0,26* 0,24 -1,11 1,41 0,24 |
-0,05 0,31 1,15* 0,91* 0,50 0,57 3,4 0,57
|
-0,01 0,45 1,21 0,54* 0,07 0,43 2,69 0,4 |
-0,28 0,22 1,47* 0,76* 0,11 0,15 2,43 0,41 |
0,25 1,9 4,35 2,47 0,92 0,04 9,93
|
0,06 0,47 1,08 0,61 0,23 0,01 0,4 |
Tabla 1.- Puntuaciones medias color por concepto de N=100.
En cada celda de esta matriz se dispone un valor obtenido de la siguiente forma: primeramente se obtiene la media de las puntuaciones de los 100 sujetos en cada una de las 12 escalas que componen un factor al evaluar un determinado color. En segundo lugar se obtiene la puntuación en el factor para cada uno de los colores sumando las correspondientes puntuaciones medias obtenidas en cada una de las escalas. En tercer lugar se obtiene el valor medio en cada factor al evaluar cada color dividiendo la puntuación obtenida en el paso anterior por el número de escalas.
A partir de esta matriz pueden obtenerse las distancias entre cada par de colores respecto a las tres dimensiones aplicando (5). El resultado puede representarse en una matriz cuadrada simétrica; en nuestro caso: (Tabla 2) con valores nulos en la diagonal principal.
|
Colores Colores |
Ocre |
Marrón |
Granate |
Azul |
Gris |
Naranja |
|
-
|
0,84 -
|
2,45 1,74 -
|
1,55 1,04 1,03 -
|
0,76 0,81 1,91 0,90 - |
1,90 2,04 1,31 1,54 1,39 -
|
Tabla 2. Distancias entre colores para N=100.
Existen varias formas de analizar e interpretar una matriz como esta última. Inicialmente Osgood Suci y Tannembaum realizaron representaciones tridimensionales de la matriz de distancias construyendo modelos reales con astillas y bolitas de goma. (Osgood, Suci y Tannembaum, 1957).
En un trabajo presentado hace unos años, Tous y Sánchez (1984) aplicaron el método de análisis en coordenadas principales (ACP) a la matriz de distancias entre 6 colores de la tabla 2. Las distancias se habían obtenido sobre cuatros factores: Antigüedad, Solidez, Seguridad y Poder.
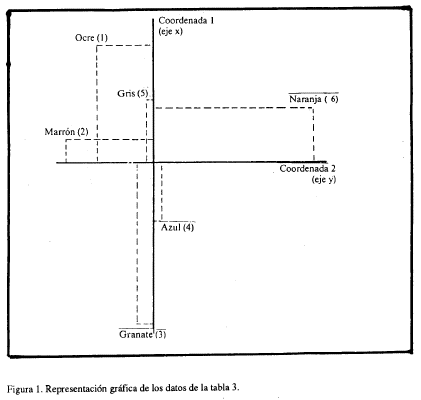
Se obtuvieron dos componentes principales que explicaban el 98% de la variabilidad contenida en la matriz de las distancias. La matriz de puntuaciones fue la siguiente: (Tabla 3).
Y su representación gráfica:
El método de componentes principales (CP) se basa en un algoritmo iterativo desarrollado por Hotteling en 1933 para extraer componentes de varianza de una matriz de interrelaciones entre variables. Aunque ha sido extensamente utilizado como método de extracción factorial, CP no tiene que partir necesariamente de una matriz de correlaciones. La extracción de los componentes se realiza a partir de dos criterios: 1) Los componentes deben ser independientes entre sí; 2) Cada componente debe explicar la mayor cantidad de varianza posible.
Este segundo criterio se obtiene resolviendo:
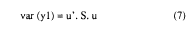
donde y1 es el primer componente u es el vector de cargas (autovector) asociado a este primer componente y S es la matriz de varianzas-covarianzas. Si normalizamos u,

La maximización de la varianza se obtiene resolviendo el problema del valor característico:

premultiplicando por u'
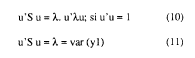
Es decir, el valor de la primera raíz latente (autovalor) corresponde a la varianza del primer componente principal.
En cuanto al primer criterio se obtiene restando a la matriz inicial la contribución del primer componente, de tal modo que el proceso iterativo para cada componente se reinicia con la matriz residual.
El resultado del método lleva a la obtención de una serie de componentes que decrecen en varianza del primero al último. Si el proceso se lleva hasta el final, se obtienen tantos componentes como variables habían inicialmente y se explica el 100% de la varianza. Normalmente el proceso se detiene en un punto (relativamente arbitrario) en el que se pueda explicar una gran proporción de variabilidad con un número reducido de componentes.
Una forma alternativa de considerar el método, más apropiada al enfoque de este trabajo, es la propuesta por Gower (1966). De acuerdo con este autor, el primer componente principal equivale a la línea que mejor se ajusta a las observaciones según el criterio de mínimos cuadrados. Everitt (1978) señala que, cuando sólo se extraen dos componentes, la distancia entre dos puntos proyectados sobre dichos componentes puede considerarse una buena aproximación a la distancia euclidiana entre dichos puntos.
El análisis de coordenadas principales (ACP) es un procedimiento desarrollado por Gower (1966) con la finalidad de obtener una serie de coordenadas para un conjunto de observaciones de tipo cualitativo. Como señala Everitt (1978) si se utiliza para variables cuantitativas, el método se hace directamente análogo a CP. ACP pretende representar distancias en una dimensión reducida y su criterio básico es el de maximizar la suma de cuadrados de las distancias (autovalores). El algoritmo de resolución es el siguiente: (Cuadras, 1981; Everitt, 1978; Gower, 1966).
a) Se parte de una matriz de similitudes o disimilitudes S
b) Se transforma esta matriz a T en la que:
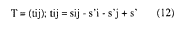
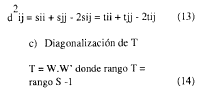
Las coordenadas principales en una dimensión d, serán las d primeras columnas de W.
ACP requiere que W sea semidefinida positiva, lo cual puede verificarse mediante el signo de los autovalores. En su estudio sobre el método, Gower (1966) señala que éste sólo puede utilizarse en caso de que W posea autovalores no-negativos. Caso de poseerlos, las distancias no son representables mediante coordenadas y se hace necesario recurrir a otros métodos de análisis. De cumplirse los requisitos que exige, el ACP tiene la ventajas de ser mucho más simple, de tener una solución algebraicamente determinada y de describir bien la estructura de los datos (Cuadras, 1981).
Tous y Sánchez (1984) pretendían utilizar ACP como una alternativa más simple a los modelos tridimensionales inicialmente utilizados por Osgood. Parecía apropiado, por tanto, representar las relaciones en un espacio bidimensional. Este criterio fijaba el número de componentes a extraer y demostró ser apropiado, en cuanto a que dos componentes bastaban para explicar el 98% de la varianza total. Por otra parte el carácter positivo de los autovalores señalaba que se cumplían los requisitos de Gower.
La solución propuesta por Gower para la obtención de las coordenadas principales es prácticamente idéntica al denominado "escalamiento multidimensional clásico" propuesto por Torgerson (1952, 1958), hasta el punto de que, en reconocimiento a la aportación independiente de ambos autores, a esta técnica se la conoce también como escalamiento de Torgerson y Gower (de Leeuw y Meulman, 1986).
Carroll y Arabie (1980) consideran que el escalamiento multidimensional (EMD en adelante) puede definirse, en un sentido amplio, como una familia de modelos geométricos para una representación multidimensional de los datos y los correspondientes métodos para ajustar los modelos a los datos reales. Entendido en un sentido más estricto, el término se referiría a modelos de distancias espaciales para disimilitudes, similitudes o proximidades en general (Duna-Rankin, 1983; Young y Hamer, 1987). Otros autores, en fin, (Davidson, 1983; McCallum, 1988; Meulman, 1986) limitan aún más el término para referirse a aquellos modelos que pretenden encontrar un espacio de dimensionalidad mínima en el que las distancias entre puntos se asemejen al máximo a las disimilitudes iniciales existentes entre las observaciones. El análisis que se presenta en este trabajo puede encuadrarse en la consideración más restringida de dichos modelos.
El método de Torgerson (1952) parte del supuesto de que las disimilitudes observadas se relacionan linealmente con las distancias euclidianas. Se asume que las disimilitudes se miden en una escala de intervalo con origen, en principio, arbitrario. Desde estos supuestos, la finalidad del método es encontrar unas coordenadas para estos puntos en un espacio de dimensionalidad mínima. El proceso para hallar dichas coordenadas se conoce con el nombre de "proceso de Young y Householder" y fue desarrollado por estos autores ya en 1938. Se considera que la principal aportación de Torgerson consistió en situar el origen de coordenadas en el centroide de los puntos (Torgerson, 1952).
Hasta ahora hemos estado relacionando dos métodos prácticamente iguales (ACP y ENID clásico) que se han desarrollado por vías independientes: análisis multivariado y escalamiento respectivamente. En ambos casos los datos se suponen medidos en una escala métrica (de intervalo o superior). También en ambos casos nos referimos a procedimientos de análisis sobre una matriz cuadrada simétrica con valores nulos en la diagonal. De acuerdo con la taxonomía propuesta por Carroll y Arabie (1980) nos estamos refiriendo a modelos unimodales de dos vías. Aún cuando actualmente las EMD pueden ser aplicadas a una gran variedad de arreglos de datos, en el presente trabajo nos limitaremos exclusivamente a este tipo de modelos, sin tomar tampoco en consideración que el programa de análisis requiera como entrada la matriz completa o bien la matriz triangular inferior o superior sin diagonal.
La principal alternativa a las técnicas hasta ahora descritas fueron los denominados métodos no métricos, de los que aquí nos interesa especialmente el EMD no métrico. Para situar los diversos métodos que estamos tratando puede ser útil el cuadro propuesto por Shepard (1966)
En el análisis concreto que estamos comentando, se cumplen los requisitos métricos planteados por Gower, lo que permite considerar como apropiado el modelo utilizado. Sin embargo, a nivel general, en los análisis de diferencial semántico subyace el problema de la consideración de los supuestos de medida. De acuerdo con Coombs (1964), la polémica acerca de si es legítimo considerar a ciertas mediciones psicológicas como medidas en escala métrica o bien si sólo pueden considerarse como estrictamente ordinales remite, en última instancia, a la falta de una teoría de la medición. Esta polémica, conocida como la de los partidarios de modelos fuertes de medida versus partidarios de modelos débiles de medida, parece estar lejos aún de ser resuelta. Sin embargo, en opinión del propio Coombs y de otros autores, en estos casos es mejor errar del lado conservador y utilizar escalas de medida más débiles para la representación.
Una posición alternativa frente a esta polémica es la de considerar que el nivel de medida no es una característica de los datos en sí, sino que depende de la interacción entre un conjunto concreto de datos y el modelo escogido para describirlos. En el marco concreto del ENID esta es la posición que defienden Takane, Young y de Leeuw (1977).
Para la elección del modelo de medida, estos autores, basándose en la noción de escalamiento óptimo de Fisher, proponen una repetición del análisis de los datos asumiendo diferentes suposiciones acerca del nivel de medida. Cuando dos análisis llegan a la misma solución con la misma bondad de ajuste, puede considerarse que el nivel apropiado de escala es el superior. Concretamente en nuestro caso, si una solución basada en escala ordinal es idéntica a una solución basada en escala métrica y posee la misma bondad de ajuste, entonces esta última puede considerarse la escala apropiada en cuanto a que, para cumplir los requisitos métricos debe, previamente, cumplir los requisitos ordinales. En el fondo, este criterio se basa en la consideración del nivel de medida como un gradiente que lleva desde nominal hasta escala de razón, de tal forma que pueden elaborarse pruebas acerca de hasta qué punto una serie particular de datos se ajusta a un nivel determinado de medida.
La alternativa al modelo clásico o métrico de Torgerson fue presentada por Shepard en 1962 (Shepard, 1962a, 1962b) y, en esencia, se refería al análisis de una matriz cuadrada simétrica de proximidades en la que las distancias interpuntuales se consideraban medidas en una escala ordinal. Quizás la principal aportación de Shepard consistió en demostrar que cuando se imponían restricciones de monotonicidad y mínima dimensionalidad (cualitativas en apariencia) podía llegarse generalmente a una solución cuantitativa (Shepard, 1962a).
El planteamiento inicial de Shepard consistía en suponer que proximidad (disimilitud concretamente en nuestro caso) y distancia se hallaban relacionadas por una función de forma desconocida y con la única restricción de ser monotónica. Más formalmente:
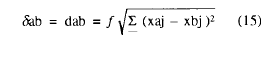
siendo f una función monotónica tal que:
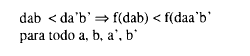
La finalidad esencial del análisis era la de hallar una configuración espacial apropiada para el conjunto de puntos en un espacio euclídeo de dimensionalidad mínima, entendiendo por apropiada aquélla en la que las distancias entre puntos guardan una relación monotónica con las medidas de disimilitud originales (Shepard, 1962b). Los objetivos podían desglosarse en tres puntos a) hallar el mínimo de dimensiones necesarias para que se cumpla la relación de monotonicidad b) obtener un sistema efectivo de coordenadas en este espacio y c) obtener un esquema relacional entre las distancias obtenidas y las disimilitudes iniciales (Shepard, 1962a).
El método de Shepard fue completado posteriormente por Kruskal (1964a, 1964). De acuerdo con Young, la principal diferencia entre los métodos de Shepard y de Kruskal consiste en que en el primero debe obtenerse previamente una representación de los n puntos en n-1 dimensiones y posteriormente reducir la dimensionalidad, mientras que en el segundo se obtiene ya de entrada una representación de los n puntos en un espacio r-dimensional donde r es mucho menor que n, y es especificado por el usuario antes del análisis. (Young y Hamer, 1987). Dado que en este trabajo utilizaremos el segundo método nos limitaremos a describir únicamente a este último.
A grandes rasgos, el proceso desarrollado por Kruskal consiste en realizar una regresión monotónica de la distancia en función de la disimilitud y normalizar la varianza residual, denominada "Stress" como función a minimizar. Se trata, en definitiva, de un ajuste de mínimos cuadrados.
Llamemos δij a la disimilitud inicial entre i y j. Supongamos esta relación simétrica δij = δji y sin coincidencias, de tal modo que sea posible ordenar las disimilitudes en orden creciente.
Los n objetos iniciales pueden representarse como n puntos
en un espacio r-dimensional (configuración). Consideraremos como euclidianas
las distancias entre los puntos, lo que implica coordenadas ortogonales. Se
pretende establecer una relación de equivalencia, de carácter
monotónico, entre las disimilitudes y las distancias. Para ello puede
partirse de un diagrama de dispersión con las disimilitudes en la ordenada
y las distancias en la abcisa, (diagrama de Shepard) p. ej.: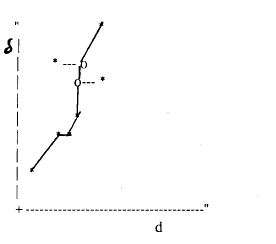
Los * representan pares de puntos. Supuesto la equivalencia monotónica, la línea que une los * debe mostrar una relación ascendente (no necesariamente lineal) de tal modo que, según se sube, la línea siempre se desplaza a la derecha pero nunca a la izquierda.
Definimos d' como pares de puntos que caen dentro de la línea (puntos ajustados) que tienen el mismo valor de δ que su * correspondiente, pero distinto valor de d. Más formalmente d' es una deformación de " mediante una función monótona creciente: d' = f (δij) (Cuadras, 1981). En el ejemplo gráfico los d'se representan por "o".
Resulta claro que, al tener la misma ", d-d' son desviaciones en sentido horizontal (---) en el gráfico.
Podemos obtener una inmediata medida global de desviación S* (Stress bruta) como Σ(d-d')2 . Kruskal propone normalizar esta medida para hacerla invariante a las expansiones dividiéndola por T* = Σd2. Definimos ahora:
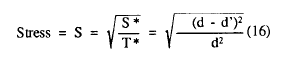
Medida que oscila entre 0 y 1 y que proporciona un indicador de la maldad de ajuste (peor cuanto más tienda a 1). Stress define el criterio para determinar la configuración de puntos (y por tanto las coordenadas de estos puntos sobre las r- imensiones), así como los valores de d'. Estos últimos serán los que minimizen S para una configuración dada. La mejor configuración en r dimensiones será aquélla entre todas las configuraciones r-dimensionales que tenga el mínimo S.
Es importante hacer notar que la evolución del stress es un indicador de la adecuación del ajuste a la dimensionalidad propuesta, equivalente a la proporción de varianza explicada cuando se utiliza el método de CP. De la misma forma que en este último n componentes explican el 100% de la varianza, en el primero se obtiene una solución exacta con n-2 dimensiones (Cuadras, 1981).
Takane, Young y de Leeuw (1977) proponen un indicador derivado del Stress de Kruskal, al que denominan SStress y que se define por:
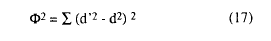
Medida equivalente al Stress bruto, salvo que éste se define en términos de distancia mientras que SStress se define en términos de distancias al cuadrado.
En el trabajo que ahora presentamos, se pretende analizar la matriz de datos obtenida en el estudio de 1984 mediante el método descrito y comparar las soluciones obtenidas en 1984 mediante ACP.
METODO
Instrumentos:
Paquete estadístico SPSS-X release 3.1. Ordenador IBM 3090 170 VM/SP CMS 5 del centro de cálculo de la Universidad de Barcelona.
Procedimiento:
En la actual investigación se ha utilizado para el análisis el algoritmo ALSCAL propuesto inicialmente por Takane, Young y de Leeuw (1977) y desarrollado posteriormente como programa por Young, Takane y Lewycky (1978). Dicho procedimiento fue incorporado en 1986 al paquete SPSS-X a partir del release 2.1 (Bisquerra, 1989). ALSCAL procede según un algoritmo iterativo flexible basado en "mínimos cuadrados alternados" (ALS) que aplica una serie de transformaciones posibles a las variables, lo que le permite trabajar desde datos nominales hasta escalas métricas (McCallum, 1988). La descripción de este procedimiento queda fuera de los límites de este trabajo, siendo suficiente considerar que, por medio de los apropiados subcomandos: input=matriz simétrica y level=ordinal, el programa realiza el análisis siguiendo el método de Kruskal. El programa utiliza como criterio para la convergencia del proceso la minimización del indicador S:Stress.
A partir de la tabla 2, la matriz de distancias entre 6 colores en el trabajo de Tous y Sánchez (1984), se aplica el algoritmo ALSCAL según el criterio de escala no métrica (level = ordinal) y definiendo previamente el número de dimensiones (2).
RESULTADOS
Puede observarse que el stress desciende hasta prácticamente 0. Este resultado indica que, para una solución bidimensional, el ajuste entre los datos y la solución es prácticamente perfecto. (Entre excelente y perfecto según el criterio propuesto por Kruskal,1964a). Adicionalmente, el máximo coeficiente d determinación entre los escalares estimados y las disimilitudes observadas indican que estas últimas explican el 100% de la variabilidad de las primeras.
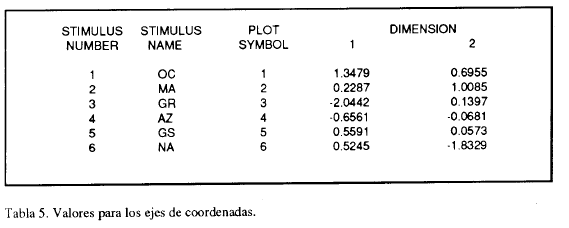

La figura 2 se presenta rotada para apreciar mejor la semejanza con la solución gráfica obtenida mediante ACP. Resulta evidente que ambas soluciones son prácticamente idénticas.
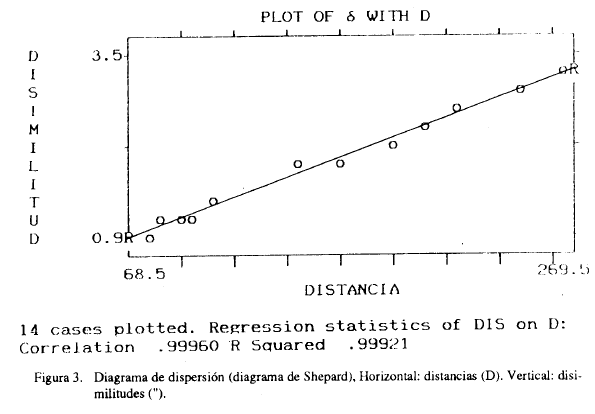
Dado que se trabaja con disimilitudes se espera una relación de tipo monotónico creciente. Adicionalmente se ha realizado un ajuste cíe regresión que señala que esta relación no sólo cumple el criterio de estricta monotonicidad, sino que, además, se ajusta claramente a un modelo lineal.
DISCUSION
Resulta evidente la similaridad entre las soluciones obtenidas en el trabajo original de 1984 mediante ACP y la actual. Asimismo esta similaridad remite a la configuración tridimensional mediante la que se interpretaron inicialmente los resultados (Tous et al, 1979). En todos los casos parece claro que los colores Ocre, Gris y Marrón presentan una relación de semejanza mayor (menor distancia) que el resto. Tous y Sánchez (1984), además, interpretaron el eje 1 como de antiguedad, eje que llevaría desde Marrón (máxima antiguedad) hasta Naranja (modernidad).
El ajuste bidimensional, prácticamente perfecto, así como la relación mostrada en el diagrama de Shepard, prácticamente lineal, podían esperarse ya a partir de los resultados obtenidos en el trabajo de 1984. Recordemos que en este último, dos dimensiones explicaban casi el 100% de la variabilidad y que todas las raíces latentes eran positivas, lo cual indicaba la adecuación a un modelo de medición métrico. El trabajo actual confirma este supuesto al señalar la elevada correspondencia entre las distancias iniciales y las obtenidas de tal modo que prácticamente no se requiere ninguna transformación (basta una iteración como señala la tabla).
En definitiva, puede considerarse que, como era de esperar, las EMD ordinales arrojan resultados similares al ACP cuando las disimilitudes iniciales se ajustan a un modelo métrico. Las ventajas de la utilización del EMD no métrico son esencialmente de dos tipos: en primer lugar resultan más generalizables, ya que pueden ser utilizables en los casos en que no se cumplan los requisitos métricos asumidos por el modelo (mientras que de cumplirse darán una solución idéntica a este último). En segundo lugar, proporcionan indicadores de la bondad (o maldad) de ajuste al modelo más elaborados que los criterios del ACP, los cuales, como se ha visto, se reducen a la proporción de varianza explicada (respecto a la dimensionalidad) y al carácter no negativo de los autovalores (respecto a la métrica).
REFERENCIAS
Bisquerra, R. (1989). Introducción conceptual al análisis multivariable. Barcelona. PPU.
Carroll, J.D. y Arabie, P. (1980). Multidimensional scaling. Annual review of psichology 31, 607-649.
Coombs, C.H. (1964). A theory of dat. New York. John Wiley.
Cuadras, C.M. (1981). Métodos de análisis multivariante. Barcelona. Eunibar.
Davidson, M.L. (1983). Multidimensional scaling. New York.
John Wiley de Leeuw, J. y Meulman, J. (1986). Principal component analysis and restricted multidimensional scaling. En Schader, W.G. (ed) Classification as a tool of research. Amsterdam. North-Holland.
Dunn-Rankin, P. (1983). Scaling methods. Hillsdale. LEA.
Everitt, B.S. (1978). Graphical techniques for multivariate data. New York. North Holland.
Fleiss, J.L. y Zubin, J. (1969). On the methods and theory of clustering. Multivariate Behavioral Research, 4, 235-250.
Gower, J.C. (1966). Some distance properties of latent root and vector methods used in multivariate analysis. Biometrika, 53, 325-338.
Kruskal, J.B. (1964a). Multidimensional scaling by optimizing goodness of fit to a nonmetric hypothesis. Psychometrika, 29, 1, 1-27.
Kruskal, J.B. (1964b). Nonmetric multidimensional scaling: a numerical method. Psychometrika, 29, 2, 115-129.
McCallum, R.C. (1988). Multidimensional Scaling. En Nesselroade y Cattell (eds). Handbook of multivariate experimental psychology. New York: Plenum Press.
Meulman, J.(1986). A distance approach to nonlinear multivariate analysis. Leiden. DSWO press.
Morlat, G (1982). Introduction a l'analyse des donnees. París. Societé de mathematiques appliquees.
Osgood, Ch. E. Suci, J. y Tannembaum, P.H. (1957). The measurement of meaning. Illinois. University of Illinois press.
Richardson, M.W. (1938). Multidimensional psychophysics. Psychological bulletin, 35, 659-660.
Shepard, R.N. (1962a). The analysis of proximities: multidimensional scaling with an unknown distance function I Psychometrika, 27, 2,125-140.
Shepard, R.N. (1962b). The analysis of proximities: multidimensional scaling with an unknown distance function II Psychometrika, 27, 3, 219-246.
Shepard, R.N. (1966). Metric structures in ordinal data Journal of mathematical psychology, 3,
287-315.
Takane, Y. Young, F y de Leeuw, J. (1977). Nonmetric individual differences multidimensional scaling: and alternative least square methods with optimal scaling features. Psychometrika, 42, 7-67.
Torgerson, W.S.(1952). Multidimensional scaling: I theory and method. Psychometrika, 17, 401-419.
Torgerson W.S. (1958). Theory and methods of scaling. New York. John Wiley.
Tous, J.M. y Sánchez, P. (1984). Aplicación del análisis de coordenadas principales a los datos obtenidos mediante la técnica del diferencial semántico. Universitas Tarraconensis, VI, (2), 151-159.
Tous, J.M. et al. (1979). Investigación sobre seis colores y su relación con los cuatro atributos: Antiguedad, Poder, Seguridad y Solidez. Barcelona: Univ. de Barna (mimeo).
Young, F.W. y Hamer, R.M.(1987) Multidimensional scaling: history, theory and applications. Hillsdale. LEA
Young, F.W., Takane, Y. y Lewyckyj, R. (1978). ALSCAL: a multidimensional scaling package with several individual differences options. Behavioral research methods and instrumentation, 10, 451-453
English