Psicothema was founded in Asturias (northern Spain) in 1989, and is published jointly by the Psychology Faculty of the University of Oviedo and the Psychological Association of the Principality of Asturias (Colegio Oficial de Psicología del Principado de Asturias).
We currently publish four issues per year, which accounts for some 100 articles annually. We admit work from both the basic and applied research fields, and from all areas of Psychology, all manuscripts being anonymously reviewed prior to publication.
Psicothema, 2004. Vol. Vol. 16 (nº 3). 509-518
Mª José Blanca Mena
Universidad de Málaga
En el análisis de datos provenientes de los diseños de medidas repetidas generalmente se utiliza el análisis de varianza mixto. Sin embargo, su adecuación está en función de la satisfacción de los supuestos asociados al análisis, en especial del supuesto de esfericidad. El objetivo del presente trabajo es realizar una revisión de las pruebas estadísticas alternativas cuando se viola el supuesto de esfericidad, incluyendo diferentes procedimientos de ajuste del estadístico F, el análisis multivariado, las pruebas de la Aproximación General y de la Aproximación General Mejorada, el procedimiento de Welch-James, el acercamiento Bayesiano y el enfoque del modelo mixto. Se realiza una discusión de estos procedimientos en términos de robustez estadística ante la violación de los supuestos para analizar los efectos principales y de interacción en diseños balanceados y no balanceados.
Approaches to the stastistical analysis of repeated measures designs. The analysis of variance is often used to assess treatment effects in repeated measures designs. However, this approach is sensitive to violations of the sphericity. This paper illustrates several statistical procedures for repeated measures designs and multisample repeated measures designs, including several adjusted F statistics, multivariate analysis of variance, General Approximate Test, Improved General Approximate Test, Welch-James procedure, the Bayes approach and mixed model analysis. These tests are discussed with respect to their robustness to violation of assumptions for main as well as interaction effects when designs are either balanced or unbalanced.
El diseño de medidas repetidas implica el registro de la variable dependiente bajo diversas condiciones. En un contexto manipulativo, estas condiciones pueden ser diferentes tratamientos experimentales u ocasiones de medidas antes, durante o después de la intervención. En un contexto no manipulativo, las medidas se registran en distintos intervalos temporales. Cuando el factor tiempo es una variable de interés, el diseño se concibe como longitudinal.
El diseño de medidas repetidas multimuestra (diseño Ax
El análisis de varianza (ANOVA) mixto univariado es el más usado en el análisis de los diseños de medidas repetidas, asumiendo que el factor intrasujeto es fijo y los sujetos aleatorios. Éste requiere satisfacer los supuestos de normalidad, independencia y esfericidad. El primero requiere que las observaciones de cada unidad de análisis sean extraídas de una población con distribución normal multivariada, el segundo supone la independencia entre las observaciones correspondientes a los distintos sujetos y el tercero implica la igualdad de varianzas de las diferencias entre los tratamientos, es decir, la matriz de covarianzas debe tener igual varianza de diferencia entre todos los pares de puntuaciones (Huynh y Feldt, 1970; Rouanet y Lepine, 1970).
En el caso multimuestra, para comprobar los efectos del factor de medidas repetidas y su interacción con el factor intersujeto se debe satisfacer lo que se denomina esfericidad multimuestra (Huynh, 1978; Mendoza, Toothaker y Crain, 1976). Ésta implica, por un lado, la homogeneidad de las matrices de covarianzas o igualdad de las matrices dentro de cada nivel del factor intersujeto y, por otro, esfericidad en la matriz de covarianzas común. Es decir, debe haber esfericidad para todos los niveles del factor de medidas repetidas dentro de cada nivel del factor intersujeto.
Cuando las asunciones del modelo univariado se satisfacen, el ANOVA mixto proporciona una prueba adecuada para comprobar los efectos del diseño en todas las variaciones de los diseños. Sin embargo, en la investigación psicológica es frecuente la violación de la esfericidad, sobre todo cuando los datos son longitudinales. Una violación típica de la esfericidad ocurre en los estudios relativos a la Psicología del Desarrollo en los que el tiempo representa la variable independiente. Cuando la variable dependiente se mide repetidamente en diferentes puntos temporales puede suceder que las correlaciones entre los pares de puntuaciones cercanas en el tiempo sean mayores que entre las lejanas, disminuyendo según las medidas se alejen en la serie (Huynh, 1978; Jaccard y Ackerman, 1985; McCall y Appelbaum, 1973; Rogan, Keselman y Mendoza, 1979; Winer, 1971). Estas diferencias en las correlaciones conducen a desigualdad en las varianzas de las diferencias. La varianza de las diferencias tiende a ser menor cuando las puntuaciones están altamente correlacionadas y mayor cuando las correlaciones son bajas (Maxwell y Delaney, 1990). McCall y Appelbaum (1973) señalan también como situaciones típicas en las que se viola la esfericidad aquellas en las que se desea medir el cambio en una variable entre diferentes condiciones experimentales en un corto período de tiempo, como en la investigación en Psicología Básica centrada en el aprendizaje. En estos experimentos las respuestas a los ensayos adyacentes frecuentemente tienen mayor correlación que los más lejanos.
Se han realizado muchos estudios mediante simulación Monte Carlo para averiguar las consecuencias de la violación de la esfericidad para el estadístico F. En general, la investigación ha indicado que la F no es robusta ante las violaciones de este supuesto, tendiendo a ser liberal (Berkovits, Hancock y Nevitt, 2000; Box, 1954; Collier, Baker, Mandeville y Hayes, 1967; Imhof, 1962; Keselman, Lix y Keselman, 1996; Keselman y Rogan, 1980; Rasmussen, 1989; Rogan, Keselman y Mendoza, 1979). Esta liberalidad implica que el uso del estadístico F puede llevar al investigador a rechazar la hipótesis nula con más frecuencia de la debida. Por otra parte, cuando se viola la esfericidad multimuestra, la F puede ser liberal o conservadora dependiendo de si la asociación entre el tamaño de los grupos (nj) y las matrices de covarianzas es negativa o positiva, respectivamente (Keselman, Lix y Keselman, 1996, Vallejo, 2003)1. Existe una relación positiva cuando el grupo con mayor nj está asociado a una matriz de covarianzas con mayores valores en sus elementos, y negativa cuando el grupo con mayor nj está asociado a una matriz de covarianzas con menores valores en sus elementos.
En los diseños unifactoriales, Box (1954) mostró que la tasa de error de Tipo I incrementa cuando la esfericidad se viola, con una relación positiva entre ellas. Señaló que el estadístico F sigue otra distribución con los grados de libertad reducidos según el factor multiplicativo épsilon (ε), el cual depende de la matriz de covarianzas de la población. Cuando el supuesto de esfericidad es satisfecho, el valor de e es igual o cercano a uno. La violación de la esfericidad es mayor cuanto más se aleje de uno y más se aproxime a su límite inferior. Geisser y Greenhouse (1958) y Greenhouse y Geisser (1959) demostraron que el límite inferior de ε es (1/p-1). Así, en un diseño unifactorial, cuando la esfericidad se satisface, el estadístico F se distribuye con (p-1) y (p-1)(N-1) grados de libertad, siendo p el número de niveles del factor de medidas repetidas y N el número de sujetos. Sin embargo, cuando ésta es violada, Box (1954) mostró que F se distribuye con ε(p-1) y ε(p-1)(N-1). Greenhouse y Geisser (1959) extendieron este resultado a los diseños de medidas repetidas multimuestra.
La comprobación del supuesto de esfericidad es el primer punto polémico en el análisis de los diseños de medidas repetidas, discusión que no es objeto del presente trabajo. Se ha propuesto comprobar el supuesto de esfericidad con la prueba W de Mauchly y el de homogeneidad de las matrices de covarianzas con la prueba M de Box. Sin embargo, algunos estudios han mostrado que son sensibles a las violaciones de la normalidad multivariada (Hopkins y Clay, 1963; Keselman, Rogan, Mendoza y Breen 1980; Korin, 1972; Olson, 1974). Igualmente, Keselman, Rogan, Mendoza y Breen (1980) encontraron que ambas pruebas tenían poco valor para determinar la elección posterior de la estrategia de análisis, de forma que algunos autores aconsejan no comprobar los supuestos y utilizar directamente algún procedimiento para corregir el posible sesgo (Keselman, Rogan, Mendoza y Breen 1980; Muller y Barton, 1989; Rogan, Keselman y Mendoza, 1979).
El lector interesado puede consultar el texto de Kirk (1995, p. 277), el cual, basándose en los resultados de Cornell, Young, Seaman y Kirk (1992), propone utilizar, para los diseños unifactoriales de medidas repetidas, la prueba Invariante Localmente Mejor (Locally Best Invariant Test) con un alfa de .15 cuando el número de sujetos es mayor o igual a 10 y de .25 cuando es menor. Para el supuesto de esfericidad multimuestra en los diseños de medidas repetidas multimuestra, Kirk (1995, p. 525) aconseja la prueba de Harris (1984) y proponen una estrategia secuencial sobre la base de los resultados encontrados en la misma.
Alternativas de análisis ante la violación de la esfericidad
Se han propuesto diferentes alternativas de análisis estadístico para los diseños de medidas repetidas cuando se viola la esfericidad. A continuación se detallan algunos de estos procedimientos.
Pruebas F ajustadas
En general, las pruebas F ajustadas consisten en reducir los grados de libertad asociados al estadístico F del ANOVA en función del factor correctivo ε. De esta forma, la F observada se compara con la F crítica con los respectivos grados de libertad del numerador y denominador multiplicados por ε. Como el valor de ε es desconocido en la población, éste debe ser estimado. Las pruebas que utilizan la F ajustada varían dependiendo del procedimiento de estimación.
a) Ajuste mediante el límite inferior de ε (Geisser y Greenhouse, 1958)
Geisser y Greenhouse (1958) propusieron el ajuste de los grados de libertad a partir del límite inferior de ε, de manera que la F observada se compara con la F crítica con los grados de libertad multiplicados por éste. Este procedimiento es muy conservador y algunos autores le llaman prueba de F conservadora (Balluerca y Vergara, 2002; Kirk, 1995; Pascual, Frías y García, 1996; Rogan, Keselman y Mendoza, 1979). Cuando el ordenador no era una herramienta para el análisis de datos y otras estimaciones de ε conllevaban una gran dificultad de cálculo, Greenhouse y Geisser (1959) propusieron una estrategia secuencial, la cual para un diseño de medidas repetidas unifactorial se aplicaría de la siguiente forma:
b) Ajuste mediante ε^ de Box (1954)
Box (1954) propuso utilizar el estimador de ε simbolizado por ε^, el cual recibe el nombre en la mayoría de los paquetes estadísticos de ε^ de Greenhouse-Geisser. Greenhouse y Geisser (1959) extendieron este procedimiento a los diseños multimuestra. El estimador de e viene dado en notación matricial por:
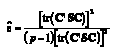 (1)
(1)
donde tr es el operador traza, C es cualquier matriz de orden px(p-1) con (p-1) coeficientes ortogonales entre medias que han sido normalizados y que expresan la hipótesis nula del factor de medidas repetidas (o en el caso multimuestra, asociadas con B y AxB) y S es la estimación de la matriz de covarianzas de la población (Σ).
Algunos autores han encontrado que ε^ subestima el valor de ε, particularmente cuando es cercano a uno, convirtiéndose en una prueba conservadora con violaciones moderadas de la esfericidad (Collier, Baker, Mandeville y Hayes, 1967; Chen y Dunlap, 1994; Huynh, 1978; Huynh y Feldt, 1976; Quintana y Maxwell, 1994; Maxwell y Arvey, 1982; Keselman y Keselman, 1990; Rogan, Keselman y Mendoza, 1979). Para corregir este sesgo, Huynh y Feldt (1976) desarrollaron otro estimador.
c) Ajuste mediante ε~ de Huynh-Feldt (1976) y ε~L de Lecoutre (1991)
A partir de ε^, Huynh y Feldt (1976) propusieron otra estimación de ε, la cual se simboliza tradicionalmente como ε~. Ésta puede sobrestimar el valor de e e incluso puede alcanzar valores superiores a 1, en cuyo caso se iguala a 1. En los diseños unifactoriales, la estimación viene dada por:
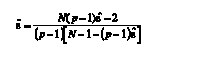 (2)
(2) donde N representa el número de sujetos y p el número de niveles del factor intrasujeto. En los diseños multimuestra, ε~ se estima según:
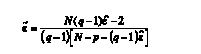 (3)
(3) donde p representa al número de niveles del factor intersujeto y q el número de niveles del factor de medidas repetidas.
Lecoutre (1991) propuso una corrección a la fórmula (3) en la que se sustituye N en el numerador por (N-p+1), cuyo estimador resultante se simboliza con ε~L. Señaló que la fórmula propuesta por Huynh y Feldt (1976) subestima la desviación de la esfericidad de la matriz de covarianzas, subestimación que puede ser sustancial cuando el número total de sujetos es pequeño.
Huynh y Feldt (1976) encontraron que ε~ era más robusto que ε^ con valores de ε mayores o superior a 0.75. Por ello, algunos autores, como Barcikowski y Robey (1984) han sugerido utilizar ε^ cuando se piense que ε es menor que 0.75 y ε~ cuando sea mayor o igual 0.75. Sin embargo, el problema radica en qué estimador de ε utilizar para determinar la estrategia. Quintana y Maxwell (1994) propusieron dos estrategias para un diseño de medidas repetidas multimuestra, a partir del uso condicional de ε^ o ε~L:
Quintana y Maxwell (1994) encontraron que los dos procedimientos arrojaban valores similares de probabilidad de cometer error de Tipo I, aunque el segundo presentaba valores más ajustados al α nominal. Chen y Dunlap (1994) hallaron que el mejor estimador de ε cuando de ε= 0.522 era ε^, independientemente del tamaño muestral o número de grupos. Sin embargo, con valores de ε= 0.752 y ε= 0.831, el estimador menos sesgado fue ε~L.
d) Ajuste ε-u de Maxwell y Arvey (1982)
Maxwell y Arvey (1982) encontraron que ε^ subestimaba el valor de ε en la población, especialmente cuando el tamaño muestral era pequeño y con valores cercanos a uno, mientras que ε~ tendía a sobrestimarlo. Estas tendencias antagónicas llevaron a los autores a proponer la media entre ambos para la estimación de ε. El nuevo estimador fue simbolizado por Quintana y Maxwell (1994) como ε-u.
e) Ajuste ε-w de Quintana y Maxwell (1994)
Quintana y Maxwell (1994) propusieron, en la línea de Maxwell y Arvey (1982), el cálculo de la media entre los dos estimadores, pero adjudicándole a cada uno una ponderación indicativa de su importancia en la estimación. Basándose en los estudios previos, partieron de la idea de que ε^ y ε
~ eran más discrepantes cuando ε= 1, por lo que en su opinión la elección de la ponderacpsilon;ión era más importante en los valores de ε cercanos a uno. Por otro lado, la ponderación debería reflejar la subestimación de ε^ y la sobrestimación de ε~. Así, el principal objetivo era encontrar un peso, w, tal que
wE(ε~)+(1 - w)E(ε~)= 1
A partir de los resultados de Muller y Barton (1989), Quintana y Maxwell (1994) derivaron el valor de w para ε= 1 y muestras grandes,
siendo p el número de niveles del factor intersujeto y q el del factor intrasujeto. Bajo las condiciones anteriormente mencionadas, la ponderación es menor a 0.50, lo que implica que ε~ recibe menos peso en la estimación que ε^. El nuevo estimador fue simbolizado como ε~w.
Análisis multivariado de la varianza (MANOVA)
El análisis multivariado requiere normalidad multivariada y homogeneidad de las matrices de covarianzas, pero no hace ninguna restricción sobre la forma de la matriz común de covarianzas, es decir, no requiere el supuesto de esfericidad. Sin embargo, el MANOVA es matemáticamente imposible cuando el total de la muestra menos el número de grupos es menor que el número de niveles de medidas repetidas menos uno. Por tanto, una importante restricción del análisis multivariado es el tamaño muestral.
Este procedimiento implica una reformulación de la matriz del diseño en un contexto multivariado, en el que las medidas repetidas se convierten en múltiples variables dependientes y los sujetos se consideran replicaciones en el diseño. Se trasforman las K variables dependientes en K-1 puntuaciones de diferencias linealmente independientes. El análisis se realiza sobre estas K-1 variables, calculándose el estadístico multivariado pertinente [Criterio de la Traza de Hotelling-Lawley (T), Traza de Pillai-Bartlett (V), Criterio de la Raíz Mayor de Roy (θ) y Lambda de Wilks (Δ)] y su respectiva aproximación a F. La aplicación del análisis multivariado al diseño de medidas repetidas puede consultarse, entre otros textos, en Arnau (1990), Arnau y Balluerca (2004), Davidson (1988), Girden (1992), Hand y Taylor, (1987), Maxwell y Delaney (1990), Tanguma (1999), Pacual, Frías y García (1996), Stevens (1996) y Vallejo (1991).
Finalmente, Algina (1994) presentó la versión multivariada del enfoque Brown-Forsythe para la interacción en el diseño de medidas repetidas multimuestra y definió cuatro estadísticos análogos a los citados anteriormente. Esta prueba también ha sido extendida al diseño multivariado de medidas repetidas por Vallejo y Escudero (2000) y Vallejo, Fidalgo y Fernández (2001).
Análisis combinado: F ajustada y MANOVA
La elección entre un análisis univariado y multivariado ha sido muy debatido en la literatura metodológica. En el dilema de escoger entre ambos, Barcikowski y Robey (1984) y Looney y Stanley (1989) propusieron un procedimiento combinado, asignando la mitad del nivel de significación a cada prueba. De esta forma, el factor de medidas repetidas se declara significativo si hay un α/2 asociado a cualquiera de las pruebas. Como prueba univariada, Barcikowski y Robey (1984) aconsejan utilizar ε^ cuando se desconoce el valor de ε en la población.
Aproximación General y Aproximación General Mejorada (Huynh, 1978)
Huynh (1978) desarrolló la prueba de la Aproximación General (General Approximate, GA) y de la Aproximación General Mejorada (Improved Generalized Approximate, IGA) como alternativas a ε^ y ε~ en el análisis de datos provenientes de los diseños de medidas repetidas multimuestra. En estos procedimientos, se compara la F observada con un valor crítico, cuyos grados de libertad vienen definidos por el tamaño de los grupos y por las matrices de covarianzas y tiene en cuenta el efecto de la violación de la esfericidad multimuestra (Keselman, Algina, Kowalchuk y Wolfinger, 1999b; Keselman, Algina, Wilcox y Kowalchuk, 2000)
Algina (1994) y Algina y Oshima (1994, 1995) presentaron la estimación de los parámetros de los grados de libertad asociados a la F, introduciendo la corrección de Lecoutre (1991) y Algina (1997) lo extendió a diferentes diseños de medidas repetidas multimuestra con múltiples factores intersujeto e intrasujeto. Asimismo, propusieron la rutina para su cálculo en el módulo PROC IML del paquete estadístico SAS.
Por otro lado, Keselman, Kowalchuk, Algina, Lix y Wilcox (2000) propusieron seguir el procedimiento IGA con estimadores robustos, con la media recortada y su estimador de la varianza y covarianza, con un mínimo de 20 sujetos por grupo. Para calcular la significación estadística asociada a la prueba sugirieron sustituir los valores críticos determinados teóricamente de la F por sus valores determinados a partir de la permutación de los datos mediante el procedimiento de remuestreo o Bootstrap.
Procedimiento multivariado de Welch-James
Keselman, Carriere y Lix (1993) y Keselman, Keselman y Shaffer (1991) propusieron el uso del procedimiento multivariado de Welch-James descrito por Johansen (1980) cuando los diseños no son balanceados y cuando hay heterogeneidad de las matrices de covarianzas para probar los efectos principales y de interacción propios de los diseños de medidas repetidas multimuestra. Esta prueba al ser multivariada no requiere que la matriz de covarianzas sea esférica. El estadístico calculado se aproxima posteriormente a una distribución F, con grados de libertad del error calculados a partir de los datos muestrales, incorporando las matrices de covarianzas y los tamaños de los grupos (Lix y Keselman, 1995; Keselman, Algina y Kowalchuk, 2002; Keselman, Algina, Kowalchuk y Wolfinger, 1999b). Posteriormente, Lix y Keselman (1995) hicieron una exposición más detallada del procedimiento para diferentes diseños intersujeto e intrasujeto. Igualmente, presentaron la rutina para el cálculo mediante el módulo PROC IML del SAS, la cual también se puede encontrar en Keselman, Carriere y Lix (1993).
Al igual que se ha comentado con los procedimientos IGA y GA, recientemente se ha propuesto el procedimiento de Welch-James con estimadores robustos de tendencia central y variabilidad, con la media recortada y su estimador de la varianza y covarianza y con el uso de los valores críticos teóricos o a partir del remuestreo (Fradette, Othman, Keselman y Wilcox, 2002; Keselman, Kowalchuk, Algina, Lix y Wilcox, 2000; Keselman, Wilcox y Lix, 2003).
Enfoque bayesiano (Boik, 1997)
Boik (1997) propuso un enfoque bayesiano en el análisis de medidas repetidas, de forma que usa un estimador bayesiano de la matriz de covarianzas a partir de una combinación lineal de estimadores univariados y multivariados (Keselman, Algina y Kowalchuk, 2001). Este procedimiento requiere que la matriz de covarianzas de todo el experimento sea esférica, pero no requiere esfericidad en todos los niveles del factor intersujeto. Este supuesto es llamado segundo estado de esfericidad. Keselman, Kowalchuk y Boik (2000) hicieron un estudio de simulación y lo compararon con otros procedimientos univariados y multivariados. Boik (1997) mostró que este acercamiento se podía comportar mejor en algunas situaciones que las F ajustadas o el análisis multivariado.
Enfoque del modelo mixto
El modelo mixto permite modelar la estructura de la matriz de covarianzas y sus diferencias entre los grupos en función de la descripción de los datos (Cnaan, Laird y Slasor, 1997: Laird y Ware, 1982; Littell, Milliken, Stroup y Wolfinger, 1996). De esta forma, la estructura de la matriz de covarianzas más adecuada se seleccionan previamente mediante algún criterio, como el AIC de Akaike o el BIC de Schwarz (Vallejo, Fernández y Velarde, 2001; Wolfinger, 1996). El SAS (PROC MIXED) permite ajustar según un patrón de simetría compuesta, no estructurado, autorregresivo de primer orden o de coeficientes aleatorios. No obstante, la principal dificultad de este procedimiento radica precisamente en la modelización correcta de las matrices de covarianzas.
Efecto de la violación de los supuestos y robustez de las alternativas de análisis
Se han realizado muchos estudios para analizar la robustez de los procedimientos anteriormente mencionados mediante la aplicación de la simulación Monte Carlo. El término robustez se refiere a la insensibilidad de la tasa de error de Tipo I y potencia de los estadísticos ante violaciones de los supuestos asociados a los mismos (Box, 1953). Para interpretar los resultados de los estudios de simulación es necesario establecer un criterio de robustez estándar que asegure la comparación de los mismos a través de las diferentes investigaciones. Sin embargo, esta situación, aunque es la ideal, no es la real. Los primeros estudios realizaban una apreciación subjetiva de la desviación entre la tasa de error de Tipo I nominal y empírica. Posteriormente, se incorporaron diferentes criterios de robustez, entre los que destacan los siguientes:
Keselman, Algina, Kowalchuk y Wolfinger (1999b) señalan que ante la ausencia de un criterio estándar, las bandas propuestas por Bradley parecen apropiadas para trabajar en investigación. Además, la mayoría de los estudios recientes de simulación realizados en el tema que nos ocupa analizan sólo la tasa de error Tipo I y utilizan este criterio, por lo que será el criterio que adoptemos para homogeneizar y realizar una discusión de los resultados encontrados en los mismos. Es necesario señalar que la adopción de este criterio puede conllevar a diferentes interpretaciones que las realizadas por los respectivos autores de los trabajos.
Por otro lado, hay que resaltar que la investigación es muy variada en cuanto a las pruebas estadísticas analizadas y variables manipuladas. Entre éstas se pueden citar el número de niveles del factor de agrupamiento y del factor de medidas repetidas, tamaño muestral total, número de sujetos por grupo, forma de la distribución de los datos, homogeneidad o no de las matrices de covarianzas entre los grupos, estructura de las matrices de covarianzas, grado de violación de la esfericidad y asociación entre el tamaño de los grupos y matrices de covarianzas. A continuación se realizará una revisión de los resultados más destacados encontrados en la investigación en términos de tasa de error de Tipo I y potencia estadística en función de estas variables.
La mayoría de los estudios se han centrado en las pruebas F ajustadas y en el análisis multivariado con diseños de medidas repetidas multimuestra, siguiendo un procedimiento jerárquico en el análisis. De esta forma, se realiza la prueba asociada al efecto de interacción entre el factor de agrupamiento y el de medidas repetidas sólo cuando éste es distinto de cero. Cuando es igual a cero, entonces sólo se realizan las pruebas asociadas a los efectos principales.
En relación con los efectos principales con diseños balanceados, se ha encontrado que las F ajustadas según ε^ y ε~ presentan tasas de error de Tipo I controladas ante violaciones de la esfericidad, tanto con datos normales y homogéneos (Chen y Dunlap, 1994) como no normales y heterogéneos (Rogan, Keselman y Mendoza, 1979) en diseños con cuatro y cinco niveles del factor de medidas repetidas. Huynh (1978) también obtuvo un buen control de la tasa de error de Tipo I con ε^ y ε~ con heterogeneidad de matrices de covarianzas, aunque encontró una tendencia de ε^ a ser conservador para valores altos de épsilon y ε~ a ser más robusto en estas situaciones. La robustez de las dos pruebas F ajustadas ante diversas violaciones de la esfericidad multimuestra también ha sido encontrada por Keselman y Keselman (1990) con diseños de ocho niveles de medidas repetidas. En un estudio de meta-análisis, Keselman, Lix y Keselman (1996) confirmaron la robustez de ε^ en una amplia variedad de condiciones.
Por otro lado, Maxwell y Arvey (1982) hallaron que cuando los diseños son balanceados, con distribuciones normales y homogeneidad de las matrices de covarianzas, el número de niveles del factor de medidas repetidas influía en la robustez ante la violación de la esfericidad y lo hacía de forma diferente para ε^ y ε~. En su estudio seleccionaron 13 niveles sobre la base del número de variables que se pueden extraer de la administración de tests tradicionalmente utilizados, como en el MMPI, donde un análisis de perfiles puede ser de interés. Los resultados mostraron que, en general, ε era conservador con valores de ε próximos a uno, mientras que ε~ era robusto, excepto para el diseño 6x13 y con dos sujetos por celdilla, en el que se mostró liberal para valores de ε ≤0,74. En esta línea, Keselman y Keselman (1990) encontraron en un diseño 3x8 con sólo una muestra total de nueve sujetos que ε^ era conservador con ε≥0,75, mientras que ε^ mostró una tendencia a la liberalidad con ε <0.75.
Estudios posteriores con diseños de 3x4 y 3x8 y un mayor número de sujetos por celdilla han corroborado la robustez de las dos F ajustadas para los efectos principales en diseños balanceados ante una variedad de valores de ε, de condiciones de heterogeneidad de las matrices de covarianzas y de distribuciones de los datos (Algina, 1994; Algina y Oshima, 1995; Keselman, Keselman y Lix, 1995; Keselman, Algina, Kowalchuk y Wolfinger, 1999b).
Con respeto a los diseños no balanceados los resultados no han sido tan acordes. Huynh (1978) obtuvo un buen control de la tasa de error de Tipo I con ε^ y ε~ bajo condiciones de normalidad y heterogeneidad de matrices de covarianzas, al igual que Keselman y Keselman (1990). Sin embargo, Algina y Oshima (1994) hallaron que ε~ era conservador cuando había una asociación positiva entre tamaño grupal y dispersión, y liberal cuando la asociación era negativa. Keselman, Keselman y Lix (1995) y Keselman, Algina, Kowalchuk y Wolfinger (1999b) encontraron los mismos resultados con ε^.
Con respecto a los otros procedimientos de F ajustadas, la investigación ha sido menor, por lo que los resultados son menos generalizables. Rogan, Keselman y Mendoza (1979) confirmaron que la prueba F conservadora se mostraba en efecto conservadora en la mayoría de las condiciones estudiadas. Keselman y Keselman (1990) encontraron que ε-u era robusto para los efectos principales en diseños balanceados y no balanceados, diferentes violaciones de la esfericidad y heterogeneidad de las matrices de covarianzas. No obstante, con muestras muy pequeñas otras investigaciones han encontrado una tendencia de ε-u a la liberalidad (Keselman, Kowalchuk y Boik, 2000). Igualmente, con diseños no balanceados ε-u presenta la misma tendencia al conservadurismo y liberalidad que ε^ y ε~, dependiendo de la asociación con el tamaño grupal (Keselman, Kowalchuk y Boik, 2000). Con respecto a ε~L, se ha encontrado que es robusto ante violaciones de la esfericidad con todos los demás supuestos satisfechos (Quintana y Maxwell, 1994). Keselman, Algina, Kowalchuk y Wolfinger (1999b) confirmaron este resultado bajo condiciones de no esfericidad, no balanceo y diferentes estructuras de las matrices de covarianzas para ε~L.
Por otro lado, en relación con el procedimiento multivariado, Rogan, Keselman y Mendoza (1979), con diseños 3x4 balanceados, encontraron que era robusto ante violaciones de la esfericidad, homogeneidad de las matrices de covarianzas y normalidad. Keselman, Keselman y Lix (1995) obtuvieron lo mismo para el procedimiento combinado, aunque éste fue siempre más conservador que el multivariado. Sin embargo, en diseños 3x8, en los que la ratio entre el tamaño grupal y número de niveles de medidas repetidas era más pequeña, estos autores encontraron que el análisis multivariado se veía afectado por la no normalidad y heterogeneidad de las matrices de covarianzas, mostrándose liberal en todos los casos estudiados, mientras que el combinado mantenía controlada la tasa de error de Tipo I. Esta liberalidad ha sido confirmada para muestras pequeñas por Keselman y Keselman (1990) y Keselman, Kowalchuk y Boik (2000).
Para diseños no balanceados, se ha verificado que el procedimiento multivariado, al igual que los univariados, es conservador ante una asociación positiva entre tamaño grupal y dispersión y liberal ante una asociación negativa, bajo condiciones de no esfericidad, no normalidad y diferentes estructuras de las matrices de covarianzas entre los grupos (Keselman, Algina, Kowalchuk y Wolfinger, 1999b; Keselman y Keselman, 1990; Keselman, Kowalchuk y Boik, 2000).
Recientemente también se ha considerado el uso de los estimadores robustos de tendencia central y dispersión para la F ajustada por ε~ (Wilcox, Keselman, Muska y Cribbie, 2000), ε^ y el análisis multivariado (Berkovits, Hancock y Nevitt, 2000) para el diseño unifactorial de medidas repetidas. En general, este procedimiento conduce a un mejor control de la tasa de error de Tipo I con diferentes violaciones de la esfericidad y normalidad.
Como algunos autores señalan, la elección entre un método univariado y multivariado descansa en consideraciones de potencia de la prueba (Stevens, 1996; Hertzog y Rovine, 1985; Vallejo, Fernández, Fidalgo, y Escudero, 1999), por lo que resulta interesante evaluar los resultados encontrados al respecto. Los estudios de potencia indican que la F ajustada mediante ε~ suele ser más potente que con ε^ (Chen y Dunlap, 1994; Maxwell y Arvey, 1982, Algina y Keselman, 1997a). Por otro lado, cuando el tamaño muestral es moderado y la matriz de covarianzas presenta leves violaciones de la esfericidad, el univariado es más potente, pero la situación se invierte según aumenta la violación de la esfericidad (Mendoza, Toothaker y Nicewander, 1974; Rasmussen, Heumann, Heumann y Botzum, 1989; Vallejo, Fidalgo y Fernández, 1998; Vallejo, Fernández, Fidalgo, y Escudero, 1999). En esta línea, Rogan, Keselman y Mendoza (1979) encontraron que el análisis multivariado era más potente ante violaciones severas de la esfericidad (ε= 0.48 y ε= 0.57). También se ha sugerido la utilización del acercamiento multivariado sólo cuando el número de sujetos sea relativamente grande (Davidson, 1972, Maxwell y Delaney, 1990). Algina y Keselman (1997a), con un diseño unifactorial de medidas repetidas con cuatro y ocho niveles, analizaron la potencia siguiendo el procedimiento propuesto por Muller y Barton (1989, 1991), y hallaron que a medida que el tamaño muestral incrementaba, el acercamiento multivariado era más poderoso que el univariado ajustado. Sobre la base de la potencia, aconsejaron el análisis multivariado cuando p≤4, N≥p+15 y ε~≤0.90 y cuando 5≤p≤8, N≥p+30 y ε~≤0.85.
Con respecto a los efectos de interacción, con diseños balanceados, los resultados son similares a los de los efectos principales. Rogan, Keselman y Mendoza (1979) encontraron que la prueba F conservadora se mostraba conservadora y que las F ajustadas mediante ε^ y ε~, así como el análisis multivariado (V, θ y Δ) eran robustos ante violaciones de la esfericidad, homogeneidad de varianzas y normalidad. Igualmente, el análisis multivariado presentó mayor potencia estadística ante violaciones severas de la esfericidad. Chen y Dunlap (1994) también mostraron que para los efectos de interacción ε^, ε~ y ε~L presentaban tasas de error de Tipo I controladas ante violaciones de la esfericidad con normalidad multivariada y homogeneidad de las matrices de covarianzas, resultados que Quintana y Maxwell (1994) replicaron para ε-u. Keselman y Keselman (1990), con datos normales, encontraron que ε^, ε~, ε-u y el análisis multivariado (V) eran robustos ante violaciones de la esfericidad multimuestra, mientras que Keselman, Algina, Kowalchuk y Wolfinger (1999b) aportaron similares datos para ε^ y V. Con datos no normales y heterogeneidad de las matrices de covarianzas, Keselman, Keselman y Lix (1995) hallaron robustez para ε^, V y el procedimiento combinado. Algina (1994) y Algina y Oshima (1994, 1995) también lo muestra para ε~. Los resultados respecto a ε^ y V son confirmados con un meta-análisis por Keselman, Lix y Keselman (1996) en una amplia variedad de condiciones.
Con datos no balanceados, los resultados son de nuevo heterogéneos. Huynh (1978), con datos normales, encontró que ε^ y ε~ eran robustos ante violaciones de la esfericidad y heterogeneidad de las matrices de covarianzas. Sin embargo, Keselman y Keselman (1990), bajo estas condiciones, encontraron que la robustez de ε^, ε~, ε-u y V dependía de la asociación entre las matrices de covarianzas y el tamaño grupal. Con asociaciones positivas, todas las pruebas resultaron conservadoras, mientras que con asociaciones negativas resultaron liberales. El efecto de la relación entre dispersión y tamaño grupal también ha sido encontrado para ε^, ε~, ε-u, ε~L, análisis multivariado y el procedimiento combinado en diseños con diferentes niveles de medidas repetidas (Algina, 1994, Keselman y Keselman, 1990: Keselman, Keselman y Lix, 1995; Keselman, Algina, Kowalchuk y Wolfinger, 1999b; Keselman, Kowalchuk y Boik, 2000).
En general, la investigación muestra que las pruebas F ajustadas o el análisis multivariado no son procedimientos adecuados cuando se viola la esfericidad en diseños no balanceados. Esta situación ha llevado a realizar estudios de simulación para analizar el comportamiento de pruebas analíticas alternativas. A continuación se expondrán los resultados de los estudios de simulación de las mismas referidos especialmente a los diseños no balanceados y a la interacción.
Diferentes investigaciones han mostrado que el procedimiento GA puede resultar conservador para algunas combinaciones de violación de la esfericidad, homogeneidad y normalidad (Huynh, 1978, Algina y Oshima, 1994), por lo que se recomienda la alternativa IGA. Algina y Oshima (1994) encontraron que ésta prueba era robusta a la violación de la esfericidad multimuestra con distribuciones normales. Sin embargo, con datos no normales, a veces podía resultar conservadora con valores de ε cercanos a uno y una ratio entre el número de sujetos y el número de medidas repetidas pequeña. Estudios posteriores, sin embargo, han mostrado la robustez de esta prueba bajo condiciones de no esfericidad, no normalidad y diferentes modelizaciones de las matrices de covarianzas, incluso con pocos sujetos (Keselman, Algina, Kowalchuk y Wolfinger, 1999b; Keselman, Kowalchuk y Boik, 2000; Keselman, Algina, Wilcox y Kowalchuk, 2000).
Por otro lado, Keselman, Kowalchuk, Algina, Lix y Wilcox (2000) compararon el procedimiento IGA con estimadores mediante mínimos cuadrados con estimadores robustos (media recortada al 20%). Para la significación estadística asociada a la prueba utilizaron los valores críticos determinados teórica y empíricamente mediante remuestreo. El estudio analizó datos balanceados y no balanceado, normales y no normales, igualdad y desigualdad de las matrices de covarianzas, con emparejamiento positivo o negativo del tamaño grupal y diferentes valores de ε. El grupo de menor tamaño tenía 20 sujetos con objeto de realizar un cálculo adecuado de la media recortada (Wilcox, 1995). Los resultados mostraron que el procedimiento IGA era robusto en todas las violaciones estudiadas y en todos los procedimientos aplicados (mínimos cuadrados o estimadores robustos). La utilización del valor crítico determinado mediante remuestreo no aportó ninguna ventaja. Keselman, Algina, Wilcox y Kowalchuk (2000), por su parte, ampliaron las condiciones de Keselman, Kowalchuk, Algina, Lix y Wilcox (2000) para diseños de 6x4 y 6x8, y encontraron de nuevo que ambos procedimientos eran robustos ante las diferentes violaciones.
En relación con la prueba multivariada de Welch-James, diversos autores han encontraron que podía ser liberal ante violaciones de la normalidad o de la homogeneidad de la matriz de covarianzas, dependiendo la robustez del tamaño muestral (Algina, 1994; Keselman, Algina, Wilcox y Kowalchuk, 2000; Keselman, Carriere y Lix, 1993; Keselman, Keselman y Lix, 1995; Keselman, Kowalchuk, Algina, Lix y Wilcox, 2000; Keselman, Kowalchuk y Boik, 2000). Así, para alcanzar la robustez de la prueba, es necesario un mínimo número de sujetos, el cual está en función del efecto del diseño y de la distribución de los datos. La recomendación de Keselman, Carriere y Lix (1993) para el efecto principal del factor de medidas repetidas es que el número de sujetos del grupo más pequeño debe ser dos o tres veces el número de medidas repetidas menos uno, si la distribución es normal, y tres o cuatro veces si no lo es. Para el efecto de interacción, la ratio debe ser de tres o cuatro para datos normales y de cinco o seis para no normales.
Otra estrategia más genérica propuesta por Keselman, Carriere y Lix (1993) consiste en utilizar un nivel de α más restrictivo. Recomiendan utilizar un α= .01, ya que proporciona un buen control del error de Tipo I con diseños mixtos 3x8, incluso cuando las matrices de covarianzas y tamaños de grupos sean desiguales o negativamente emparejadas, e incluso cuando la ratio entre el tamaño del grupo más pequeño y el número de medidas repetidas menos uno sólo sea de dos.
Algina y Keselman (1997b) revisaron la robustez de la prueba de Welch-James, ampliando las condiciones de estudio de Keselman, Carriere y Lix (1993). Los datos indicaron que para la interacción el número de sujetos necesitados para alcanzar la robustez debería ser mayor que los indicados por estos autores. De esta forma, dependiendo de las condiciones de la heterogeneidad de las matrices de covarianzas y de la violación de la esfericidad, con datos normales la ratio debería ser de cinco y para los no normales entre 6.57 y 14, condiciones que son difíciles de alcanzar en la investigación en Ciencias del Comportamiento. Igualmente, Keselman, Algina, Kowalchuk y Wolfinger (1999a, 1999b) con diseños no balanceados, bajo condiciones de no esfericidad, no normalidad y diferentes modelizaciones de las matrices de covarianzas, encontraron que para los efectos de interacción la prueba de Welch-James era liberal cuando el tamaño del grupo y la dispersión estaban negativamente emparejados, indicando que se requiere un mayor número de sujetos para el control de la tasa de error de Tipo I cuando la normalidad y homogeneidad se violan conjuntamente.
En relación con la potencia, Algina y Keselman (1998) hallaron que, cuando el número de sujetos era suficiente para que la prueba de Welch-James pudiera controlar la tasa de error de Tipo I, este procedimiento era en la mayoría de los casos, tanto en los efectos principales como de interacción, más potente que IGA bajo diferentes condiciones de desigualdad de los grupos y violación de esfericidad multimuestra y normalidad. También encontraron que la prueba de Welch-James y el procedimiento IGA no presentaban pérdida de poder cuando se utilizaban bajo condiciones de homogeneidad de las matrices de covarianzas, en comparación con la F ajustada por ε~ o el análisis multivariado. El balance entre potencia y error de Tipo I lleva a algunos autores a recomendar sistemáticamente la prueba de Welch-James (Keselman, Algina, Kowalchuk y Wolfinger, 1999a, 1999b; Keselman, Algina, Wilcox y Kowalchuk, 2000; Keselman, Keselman y Lix, 1995).
Finalmente, Keselman, Kowalchuk, Algina, Lix y Wilcox (2000) y Keselman, Algina, Wilcox y Kowalchuk (2000) analizaron el comportamiento de la prueba de Welch-James con estimadores robustos, con la media recortada al 20%, y con los valores críticos determinados teórica o empíricamente. Los resultados mostraron que era robusta con este procedimiento y que el grupo con menor número debería tener a menos 22 sujetos.
Con respecto al procedimiento multivariado de Brown-Forsythe, Algina (1994), con datos normales y no balanceados, encontró un mejor ajuste a la tasa de error de Tipo I de todas sus aproximaciones al estadístico F que la prueba de Welch-James. Sin embargo, con muestras pequeñas y una relación negativa entre tamaño muestral y dispersión, las aproximaciones se mostraron conservadoras, siendo más conservadora la análoga a la traza de Pillai y la más robusta la análoga a la traza de Lawley-Hotelling. Esta prueba sólo violó el criterio de Bradley una vez. Vallejo, Fernández y Velarde (2001), con distribuciones normales, y diseños no balanceados hallaron que la análoga a la Δ de Wilks era robusta, tanto en la interacción como en los efectos principales, ante diferentes estructuras de matrices de covarianzas.
En cuanto al enfoque del modelo mixto, Keselman, Algina, Kowalchuk y Wolfinger (1999a) lo analizaron bajo datos balanceados y no balanceados, diferentes estructuras de las matrices de covarianzas, igualdad o desigualdad de las estructuras de las matrices, diferentes tamaños muestrales, emparejamiento positivo o negativo de las matrices y tamaño grupal y datos normales y no normales. Los resultados indicaron que en el enfoque del modelo mixto, la prueba F con los grados de libertad corregidos mediante la técnica Satterthwaite era liberal cuando la estructura de las matrices de covarianzas se determinaba según el criterio de Akaike. Sin embargo, resultó robusta ante la no normalidad, datos no balanceados y heterogeneidad de covarianzas cuando las prueba se basaban en ajustes correctos de las estructuras de las matrices. Los autores concluyeron que existen problemas en la identificación de la estructura correcta que siguen los datos, por lo que aconsejan la prueba de Welch-James porque no es necesario saber la estructura de las matrices en los datos. Keselman, Algina, Kowalchuk y Wolfinger (1998) también comprobaron que ningún criterio (Akaike o Schwarz) proporcionaba selecciones adecuadas de las matrices de covarianzas.
Por otro lado, Vallejo, Fernández y Velarde (2001), siguiendo el mismo procedimiento que el estudio anterior, con distribuciones normales, diseños no balanceados y con diferentes estructuras de matrices hallaron que el modelo mixto controlaba la tasa de error de Tipo I según el criterio de Bradley. Sin embargo, también llaman la atención sobre la dificultad en la especificación de la estructura de las matrices de covarianzas. Vallejo, Fernández y Ato (2003) encontraron que el modelo mixto era más potente que la prueba multivariada de Brown-Forsythe cuando la estructura de las matrices de covarianzas estaba correctamente identificada, aunque la ventaja en la potencia disminuía al incrementar el tamaño.
Finalmente, el acercamiento bayesiano propuesto por Boik (1997) ha sido poco estudiado. Boik (1997) encontró que era más potente que las pruebas F ajustadas o que el análisis multivariado. Sin embargo, Keselman, Kowalchuk y Boik (2000) encontraron que la prueba era muy sensible a la violación de la normalidad. Con datos no normales, la prueba tendía a ser liberal o conservadora, dependiendo de si el emparejamiento entre la dispersión y el tamaño grupal era negativo o positivo.
Conclusión
Las investigaciones revisadas muestran la necesidad de utilizar un número suficiente de sujetos que permita realizar una prueba robusta ante las diferentes violaciones de los supuestos del análisis. Por otro lado, en los diseños de medidas repetidas multimuestra se evidencia la preferencia por los datos balanceados, incluyendo el mismo número de sujetos en cada nivel del factor de agrupamiento.
Con diseños balanceados, el uso de las pruebas F ajustadas son alternativas viables ante violaciones de la esfericidad para comprobar los efectos principales y de interacción. El análisis multivariado sólo resulta adecuado cuando hay un elevado número de sujetos, ya que no es robusto para la interacción si el número de sujetos es pequeño en relación con el número de medidas repetidas (Keselman, Keselman y Lix, 1995, Keselman y Keselman, 1990; Keselman, Kowalchuk y Boik, 2001). Con diseños no balanceados, no se puede recomendar el uso generalizado de estas pruebas. Hay que tener en cuenta la dirección de la asociación entre el tamaño grupal y las matrices de covarianzas. Sin embargo, incluso en estas circunstancia, todavía se pueden adoptar decisiones estadísticas correctas para la interacción con el uso de las pruebas F ajustadas o con el análisis multivariado. Así, si las matrices de covarianzas están asociadas positivamente con el tamaño grupal y el efecto de interacción es significativo, entonces el investigador podrá adoptar este resultado como válido, ya que todas las pruebas son conservadoras. En caso contrario, debe optar por otro análisis que sea menos sensible a esta condición. El mismo razonamiento pero a la inversa, se puede aplicar cuando existe un emparejamiento negativo. En estos casos, sólo si la decisión estadística lleva a la aceptación de la hipótesis nula, el analista puede considerar correcta esta decisión, ya que todos los procedimientos son liberales.
Ante los casos en los que no se recomienda las pruebas F ajustadas o el análisis multivariado, quizá los procedimientos de la Aproximación General Mejorada y el de Welch-James se conviertan en alternativas adecuadas de análisis, aunque el segundo requiere un mayor número de sujetos. El enfoque del modelo mixto, por su parte, tiene el problema de la identificación correcta de la estructura de las matrices de covarianzas. En relación con el acercamiento bayesiano y con la prueba multivariada de Brown-Forsythe todavía es necesario realizar más estudios que analicen su robustez ante las diferentes violaciones de los supuestos. Los contrastes entre medias, tras un efecto significativo, después de aplicar algunas de las pruebas citadas se pueden encontrar, entre otros, en Algina y Keselman (1997b), Keselman (1982, 1994), Keselman y Keselman (1988a, 1988b), Keselman, Keselman y Shaffer (1991), Keselman y Lix (1995), Kowalchuk y Keselman (2001), Lix y Keselman (1996), Maxwell (1980) y Scheirs (1992).
Una alternativa que no ha sido tratada en el presente trabajo es el análisis no paramétrico. El lector interesado puede consultar algunas propuestas para los diseños de medidas repetidas en Akritas (1990, 1991, 1993), Akritas y Arnold (1994), Brunner, (1991), Brunner y Dette (1992), Harwell y Serlin (1997), Kepner y Robinson (1988), Puri y Sen (1967), Rasmussen (1989), Rasmussen, Heumann, Heumann, y Botzum (1989), Thompson (1991a, 1991b) y Thompson y Ammann (1990).
Finalmente, es necesario apuntar que los comentarios y conclusiones realizados han sido extraídos de diversos estudios de simulación Monte Carlo que manipulan distintas variables y analizan diversas violaciones de los supuestos de forma separada o conjunta. Por tanto, aunque se ha deseado establecer líneas generales de actuación, éstas sólo son aplicables a las condiciones examinadas en los respectivos estudios. El lector interesado debería consultar las fuentes originales para analizar la adecuación de la prueba elegida en función del diseño y del comportamiento de los datos obtenidos.
Nota
1 Esta relación fue demostrada por el Dr. Vallejo (2003) en un estudio de simulación realizado expresamente para la revisión del presente trabajo.
Akritas, M.G. (1990). The rank transform methods in some two-factor designs. Journal of the American Statistical Association, 85, 73-78.
Akritas, M.G. (1991). Limitations of the rank transform procedure: A study of repeated measures designs, Part I. Journal of the American Statistical Association, 85, 73-78.
Akritas, M.G. (1993). Limitations of the rank transform procedure: A study of repeated measures designs, Part II. Statistics & Probability Letters, 17, 149-156.
Akritas, M.G. y Arnold, S.F. (1994). Fully nonparametric hypotheses for factorial designs. I: Multivariate repeated measures designs. Journal of the American Statistical Association, 89, 336-343.
Algina, J. (1994). Some alternative approximative tests for a split-plot design. Multivariate Behavioral Research, 29, 365-384.
Algina, J. (1997). Generalization of Improved General Approximation tests to split-plot designs with multiple between-subject factors and/or multiple within-subject factors. British Journal of Mathematical and Statistical Psychology, 50, 243-252.
Algina, J. y Keselman, H.J. (1997a). Detecting repeated measures effects with univariate and multivariate statistics. Psychological Methods, 2(2), 208-218.
Algina, J. y Keselman, H.J. (1997b). Testing repeated measures hypotheses when covariate matrices are heterogeneous: Revisiting the robustness of the Welch-James test. Multivariate Behavioral Research, 32(3), 255-274.
Algina, J. y Keselman, H.J. (1998). A power comparison of the Welch-James and Improved General Approximation test in the split-plot design. Journal of the Educational and Behavioral Statistics, 23(2), 152-159.
Algina, J. y Oshima, T.C. (1994). Type I error rates for Huynh’s General Approximation tests and Improved General Approximation tests. British Journal of Mathematical and Statistical Psychology, 47, 151-165.
Algina, J. y Oshima, T.C. (1995). An improved general approximation test for the main effect in a split-plot design. British Journal of Mathematical and Statistical Psychology, 48, 149-160.
Arnau, J. (1990). Diseños experimentales multivariables. Madrid: Alianza Psicología.
Arnau, J. y Balluerca, N. (2004). Análisis de datos longitudinales y de curvas de crecimiento. Enfoque clásico y propuestas actuales. Psicothema, 16, 156-162.
Barcikowski, R.S. y Robey, R.R. (1984). Decisions in single group repeated measures analysis: Statistical tests and three computer packages. The American Statistician, 38(2), 148-150.
Berkovits, I., Hancock, G.R. y Nevitt, J. (2000). Bootstrap resampling approaches for repeated measure designs: Relative robustness to sphericity and normality violations. Educational and Psychological Measurement, 60(6), 877-892.
Boik, R.J. (1997). Analysis of repeated measures under second-stage sphericity: An empirical Bayes approach. Journal of Educational and Behavioral Statistics, 22(2), 155-192.
Box, G.E.P. (1953). Non-normality and tests on variances. Biometrika, 40, 318-335.
Box, G.E.P. (1954). Some theorems on quadratic forms applied in the study of analysis of variance problems II. Effect of inequality of variance and of correlation of error in the two way classification. Annals of Mathematical Statistics, 25, 484-498.
Bradley, J.V. (1978). Robustness? British Journal of Mathematical and Statistical Psychology, 31, 144-152.
Balluerca, N. y Vergara, A.I. (2002). Diseños de investigación experimental en Psicología. Madrid: Prentice-Hall.
Brunner, E. (1991). A nonparametric estimator of the shift effect for repeated observations. Biometrics, 47, 1.149-1.153.
Brunner, E. y Dette, H. (1992). Rank procedure for the two-factor mixed model. Journal of the American Statistical Association, 87, 884-888.
Chen, S.R. y Dunlap, W.P. (1994). A Monte Carlo study on the performance of a corrected formula for e~ suggested by Lecoutre. Journal of Educational Statistics, 19, 119-126.
Cnaan, A., Laird, N.M. y Slasor, P. (1997). Using the general linear mixed model to analyze unbalanced repeated measures and longitudinal data. Statistics in Medicine, 16, 2.349-2.380.
Collier, R.O., Baker, F.B., Mandeville, G.K. y Hayes, T.F. (1967). Estimates of test size for several test procedures based on conventional variance ratios in the repeated measures design. Psychometrika, 32, 339-353.
Cornell, J.E., Young, D.M., Seaman, S.L. y Kirk, R.E. (1992). Power comparisons of eight tests for sphericity in repeated measures designs. Journal of Educational Statistics, 17, 233-249.
Davidson, M.L. (1972). Univariate versus multivariate test in repeated measures experiments. Psychological Bulletin, 77, 446-452.
Davidson, M.L. (1988). The multivariate approach to repeated measures. Technical report 75. Los Angeles, CA: BMDP Statistical Software, Inc.
Fradette, K., Othman, A.R., Keselman, H.J., Wilcox, R.R. (2002, julio). Comparing measures of the «typical» score across treatment group. Trabajo presentado en The Joint Statistical Meetings. Nueva York.
Geisser, S. y Greenhouse, S.W. (1958). An extension of Box’s results on the use of the F distribution in multivariate analysis. The Annals of Mathematical Statistics, 29, 885-891.
Girden, E.R. (1992). ANOVA repeated measure. London: Sage Publications, Inc.
Greenhouse, S.W. y Geisser, S. (1959). On methods in the analysis of profile data. Psychometrika, 24, 95-112.
Hand, D.J. y Taylor, C.C. (1987). Multivariate analysis of variance and repeated measures. London: Chapman and Hall.
Harris, P. (1984). An alternative test for multisample sphericity. Psychometrika, 49, 273-275.
Harwell, M.R. y Serlin, R.C. (1997). An empirical study of five multivariate tests for the single factor repeated measures model. Communications in Statistics-Simulation and Computation, 26, 605-618.
Hertzog, C. y Rovine, M. (1985). Repeated-measures analysis of variance in developmental research: Selected issues. Child Developmental, 56, 787-809.
Hopkins, J.W. y Clay, P.P.F. (1963). Some empirical distributions of bivariate T2 and homoscedasticity criterion M under unequal variance and leptokurtosis. Journal of the American Statistical Association, 58, 1.048-1.053.
Huynh, H. (1978). Some approximate tests for repeated measurement designs. Psychometrika, 43(2), 161-175.
Huynh, H. y Feldt, L.S. (1970). Conditions under which mean square ratios in repeated measurement designs have exact F-Distribution. Journal of the American Statistical Association, 65, 1.582-1.589.
Huynh, H. y Feldt, L.S. (1976). Estimation of the Box correction for degrees of freedom form sample data in the randomized block and split-plot design. Journal of Educational Statistics, 1, 69-82.
Imhof, J.P. (1962). Testing de hypothesis of o fixed main-effects in Scheffé mixed model. The Annals of Mathematical Statistics, 33, 1.085-1.095.
Jaccard, J. y Ackerman, L. (1985). Repeated measures analysis of means in clinical research. Journal of Consulting and Clinical Psychology, 53(3), 426-428.
Johansen. S. (1980). The Welch-James approximation to the distribution of the residual sum of squares in a weighted linear regression. Biometrika, 67, 85-92.
Kepner, J.L. y Robinson, D.H. (1988). Nonparametric methods for detecting treatment effect in repeated measures designs. Journal of The American Statistical Association, 83, 456-461.
Keselman, H.J. (1982). Multiple comparisons for repeated measures means. Multivariate Behavioral Research, 17(1), 87-92.
Keselman, H.J. (1994). Stepwise and simultaneous multiple comparison procedures of repeated measures’ means. Journal of Educational Statistics, 19(2), 127-162.
Keselman, H.J., Algina, J. y Kowalchuk, R.K. (2001). The analysis of repeated measures designs: A review. British Journal of Mathematical and Statistical Psyhology, 54, 1-20.
Keselman, H.J., Algina, J. y Kowalchuk, R.K. (2002). A comparison of data analysis strategies for testing omnibus effects in higher-order repeated measures designs. Multivariate Behavioral Research, 37(3), 331-357.
Keselman, H.J., Algina, J., Kowalchuk, R.K. y Wolfinger, R.D. (1998). A comparison of two approaches for selecting covariance structures in the analysis of repeated measurements. Communications in Statistics - Computation and Simulation, 27, 591-604.
Keselman, H.J., Algina, J., Kowalchuk, R.K. y Wolfinger, R.D. (1999a). The analysis of repeated measurements: A comparison of the mixed model Satterthwaite F test and a nonpooled adjusted degree of freedom multivariate test. Communications in Statistics - Theory and Methods, 28(12), 2.976-2.999.
Keselman, H.J., Algina, J., Kowalchuk, R.K. y Wolfinger, R.D. (1999b). A comparison of recent approaches to the analysis of repeated measurements. British Journal of Mathematical and Statistical Psychology, 52, 63-78.
Keselman, H.J., Algina, J., Wilcox, R.R. y Kowalchuk, R.K. (2000). Testing repeated measures hypothesis when covariance matrices are heterogeneous: Revisiting the robustness of the Welch-James test again. Educational and Psychological Measurement, 60(6), 925-938.
Keselman, H.J., Carriere, K.C. y Lix, L.M. (1993). Testing repeated measures hypotheses when covariance matrices are heterogeneous. Journal of Educational Statistics, 18(4), 305-319.
Keselman, H.J. y Keselman, J.C. (1988a). Comparing repeated measures means in factorial designs. Psychophisiology, 25(5), 612-618.
Keselman, H.J. y Keselman, J.C. (1988b). Repeated measures multiple comparison procedures: Effect of violating multisample sphericity in unbalanced designs. Journal of Educational Statistics, 13(3), 215-226.
Keselman, J.C. y Keselman, H.J. (1990). Analysis unbalanced repeated measures designs. British Journal of Mathematical and Statistical Psychology, 43, 265-282.
Keselman, H.J., Keselman, J.C. y Lix, L.M. (1995). The analysis of repeated measures: Univariate test, multivariate, or both? British Journal of Mathematical and Statistical Psychology, 48, 319-338.
Keselman, H.J., Keselman, J.C. y Shaffer, J.P. (1991). Multiple comparisons of repeated measures means under violation of multisample sphericity. Psychological Bulletin, 110(1), 162-170.
Keselman, H.J., Kowalchuk, R.K., Algina, J., Lix, L.M. y Wilcox, R.R. (2000). Testing treatment effects in repeated measures designs: Trimmed means and bootstrapping. British Journal of Mathematical and Statistical Psychology, 53, 175-191.
Keselman, H.J., Kowalchuk, R.K., y Boik, R.J. (2000). An examination of the robustness of the empirical Bayes and other approaches for testing main and interaction effects in repeated measures designs. British Journal of Mathematical and Statistical Psychology, 53, 51-67.
Keselman, H.J. y Lix, L.M. (1995). Improved repeated measures stepwise multiple comparison procedure. Journal of Educational and Behavioral Statistics, 20(1), 83-89.
Keselman, J.C., Lix, L.M. y Keselman, H.J. (1996). The analysis of repeated measurements: A quantitative research synthesis British Journal of Mathematical and Statistical Psychology, 49, 275-298.
Keselman, H.J. y Rogan, J. (1980). Repeated measures F test and psychophysiological research: Controlling the number of false positives. Psychophysiology, 17, 499-503.
Keselman, H.J., Rogan, J., Mendoza, J.L. y Breen, L.J. (1980). Testing the validity conditions of repeated measures F test. Psychological Bulletin, 87(3), 479-481.
Keselman, H.J., Wilcox, R.R. y Lix, L.M. (2003). A Generally robust approach to hypothesis testing in independent and correlated group designs. Psychophysiology, 40(4), 586-596.
Kirk, R.E. (1995). Experimental design. Procedures for the behavioral sciences (3ª ed). California: Brooks/Cole Publishing Company.
Korin, B.P. (1972). Some comments on the homoscedasticity criterion M and the multivariate analysis of variance test, T2, W, and R. Biomerika, 59, 215-216.
Kowalchuk, R.K. y Keselman, H.J. (2001). Mixed-model pairwise multiple comparisons of repeated measures means. Psychological Bulletin, 6(3), 282-296.
Laird, N.M. y Ware, J.H. (1982). Random effects models for longitudinal data. Biometrics, 38, 963-974.
Lecoutre, B. (1991). A correction of e~ approximate test in repeated measures designs with two or more independent groups. Journal of Educational Statistics, 16, 371-372.
Littell, R.C., Milliken, G.A., Stroup, W.W. y Wolfinger, R.D. (1996). SAS System for mixed models. Caary, NC: SAS Institute Inc.
Lix, L.M. y Keselman, H.J. (1995). Approximate degrees of freedom test: A unified perspective on testing for mean equality. Psychological Bulletin, 117(3), 547-560.
Lix, L.M. y Keselman, H.J. (1996). Interaction contrasts in repeated measures designs. British Journal of Mathematical and Statistical Psychology, 49, 147-162.
Looney, S.W. y Stanley, W.B. (1989). Exploratory repeated measures analysis for two or more groups: Review and update. The American Statistician, 43, 220-225.
Maxwell, S.E. (1980). Pairwise multiple comparisons in repeated measures designs. Journal of Educational Statistics, 5(3), 269-287.
Maxwell, S.E. y Arvey, R.D. (1982). Small sample profile analysis with many variables. Psychological Bulletin, 92, 778-785.
Maxwell, S.E. y Delaney, H.D. (1990). Designing experiments and analyzing data. California: Wadsworth Publishing Company.
Mendoza, J.L., Toothtaker, L.E. y Crain, B.R. (1976). Necessary and sufficient conditions for F ratios in the LxJxK factorial design with two repeated factors. Journal of the American Statistical Associations, 71, 992-993.
McCall, R.B. y Appelbaum, M.I. (1973). Bias in the analysis of repeated-measures designs: Some alternative approaches. Child Development, 44, 401-415.
Mendoza, J.L., Toothtaker, L.E. y Crain, B.R. (1976). Necessary and sufficient conditions for F ratios in the LxJxK factorial design with two repeated factors. Journal of the American Statistical Associations, 71, 992-993.
Mendoza, J.L., Toothtaker, L.E. y Nicewander, W.A. (1974). A Monte Carlo comparison of the univariate and multivariate methods for the groups by trials repeated-measures desing. Multivariate Behavioral Research, 9, 165-177.
Muller, K.E. y Barton, C.N. (1989). Approximate power for repeated measures ANOVA lacking sphericity. Journal of the American Statistical Association, 84, 549-555.
Muller, K.E. y Barton, C.N. (1991). Correction to approximate power for repeated measures ANOVA lacking sphericity. Journal of the American Statistical Association, 86, 255-256.
Olson, C.L. (1974). Comparative robustness of six tests in multivariate analysis of variance. Journal of the American Statistical Association, 69, 894-908.
Pascual, J., Frías, M.D. y García, F. (1996). Manual de Psicología Experimental. Barcelona: Ariel.
Puri, H.L. y Sen, K.L. (1967). On some optimum nonparametric procedures in two-way layouts. Journal of the American Statistical Association, 62, 1.214-1.230.
Quintana, S.M. y Maxwell, S.E. (1994). A Monte Carlo comparison of seven e-adjustement procedures in repeated measures designs with small sample sizes. Journal of Educational Statistics, 19(1), 57-71.
Rasmussen, J.L. (1989). Parametric and non-parametric analysis of groups by trials design under variance-covariance inhomogeneity. British Journal of Mathematical and Statistical Psychology, 42, 91-102.
Rasmussen, J.L. Heumann, K.A., Heumann, M.T. y Botzum, M. (1989). Univariate and multivariate groups by trials analysis under violations of variance-covariance and normality assumptions. Multivariate Behavioral Research, 24, 93-105.
Rogan, J.C., Keselman, H.J. y Mendoza, J.L. (1979). Analysis of repeated measurements. British Journal of Mathematical and Statistical Psychology, 32, 269-286.
Rouanet, H. y Lepine, D. (1970). Comparison between treatments in a repeated measures design: ANOVA and multivariate methods. British Journal of Mathematical and Statistical Psychology, 23, 147-163.
Scheirs, J.G. (1992). A priori and a posteriori tests on repeated measurements. Educational Psychology, 12(1), 63-72.
Stevens, J. (1996). Applied multivariate statistics for the social sciences (3rd. ed.). Hillsdale, N.J.: Erlbaum.
Tanguma, J. (1999). Analyzing repeated measures designs using univariate and multivariate methods. A primer. En B. Thompson, Advances in social science methodology (vol. 5, pp. 233-250). Stamford: JAI Press, Inc.
Thompson, G.L. (1991a). A unified approach to rank test for multivariate and repeated measures designs. Journal of the American Statistical Association, 86, 410-419.
Thompson, G.L. (1991b). A note on the rank transform for interaction. Biometrika, 78, 697-701.
Thompson, G.L. y Ammann, L.P. (1990). Efficiences of interblock rank statistics for repeated measures designs. Journal of the American Statistical Association, 85, 519-528.
Vallejo, G. (1991). Analisis univariado y multivariado de los diseños de medidas repetidas de una sola muestra y de muestras divididas. Barcelona: PPU.
Vallejo, G. y Escudero (2000). An examination of the robustness of the modified Brown-Forsythe and the Welch-James tests in the multivariate split-plot designs. Psicothema, 12(4), 701-711.
Vallejo, G., Fernández, M.P. y Ato, M. (2003). Tasas de potencia de dos enfoques robustos para analizar datos longitudinales. Psicológica, 24, 109-122.
Vallejo, G., Fernández, M.P. y Velarde, H. (2001). Un estudio comparativo de pruebas robustas para el análisis de datos longitudinales. Metodología de las Ciencias del Comportamiento, 3(1), 35-52.
Vallejo, G., Fernández, M.P., Fidalgo, A.M. y Escudero, J.R. (1999). Comparación de la robustez de cuatro pruebas en un diseño multivariado split-plot. Metodología de las Ciencias del Comportamiento, 1(1), 1-23.
Vallejo, G., Fidalgo, A.M. y Fernández, P. (1998). Efectos de la no esfericidad en el análisis de diseños multivariados de medidas repetidas. Anales de Psicología, 14(2), 249-268.
Vallejo, G., Fidalgo, A.M. y Fernández, P. (2001). Effects of covariance heterogeneity on three procedures for analyzing multivariate repeated measures designs. Multivariate Behavioral Research, 36(1), 1-27.
Wilcox, R.R. (1995). Three multiple comparison procedures for trimmed means. Biometrical Journal, 37, 643-656.
Wilcox, R.R., Keselman, H.J., Muska, J. y Cribbie, R. (2000). Repeated measures ANOVA: Some new results on comparing trimmed means and means. British Journal of Mathematical and Statistical Psychology, 53, 69-82.
Winer, B.J. (1971). Statistical principles in experimental design (2nd. ed.). New York: McGraw-Hill.
Wolfinger, R.D. (1996). Heterogeneous variance-covariance structures for repeated measures. Journal of Agricultural, Biological and Environmental Statistics, 1(2), 205-2.230.
English