Psicothema was founded in Asturias (northern Spain) in 1989, and is published jointly by the Psychology Faculty of the University of Oviedo and the Psychological Association of the Principality of Asturias (Colegio Oficial de Psicología del Principado de Asturias).
We currently publish four issues per year, which accounts for some 100 articles annually. We admit work from both the basic and applied research fields, and from all areas of Psychology, all manuscripts being anonymously reviewed prior to publication.
Psicothema, 1999. Vol. Vol. 11 (nº 3). 561-572
Manuel Suero Suñe
Universidad Autónoma de Madrid
Frente a los modelos que explican cómo el Sistema Visual Humano resuelve el problema de la apertura (Adelson y Movshon, 1982; Wilson, Ferrera y Yo, 1992), se propone una solución alternativa. Mientras que los primeros asumen un proceso en dos etapas jerarquizadas, la solución alternativa defiende la existencia de una sola etapa. Para evaluar si es factible, se ha realizado un experimento donde los estímulo utilizados fueron enrejados sinusoidales en movimiento. Éstos se han diseñado de forma que la percepción que producen, según los modelos estándar, es totalmente diferente a la propuesta por la solución alternativa; los primeros predicen la percepción de un estímulo con movimiento horizontal más parpadeo, el segundo la percepción de bandas con dirección de movimiento opuesta. Los resultados obtenidos parecen apoyar la solución alternativa.
The aperture problem: an alternative solution. A new explanation on how the human visual system solves the aperture problem is proposed. It has a more simple structure than classical models (Adelson y Movshon, 1982; Wilson, Ferrera y Yo, 1992). Whereas these defend a processing in two steps, the new solution assumes just one. One experiment has been running in order to test if this new explanation is feasible. Stimuli used in the experiment were moving sinusoidal gratings. These were designed to produce different perception predictions of the stimuli, if either classical models or the new solution was accepted. The first would predict a perception of a moving horizontal plaid with a flickering background. The new solution predicts a more complex perception: a stack of horizontal strips with opposite directions of motion. The experiment results seem to support the new solution.
El Sistema Visual Humano (SVH) es capaz de determinar la dirección del movimiento mediante una serie de unidades que poseen una estructura bilocal (Adelson y Bergen, 1985; van Santen y Sperling, 1985), donde cada una de ellas es sensible a una escala espacial, o rango de frecuencias espaciales, y a un rango de orientaciones ( Anderson y Burr, 1989, 1991; Anderson, Burr y Morrone, 1991). Cada unidad opera de forma local, teniendo asociada un campo receptor centrado en un punto de la retina. Además, en un mismo punto de la retina existen distintas unidades, cada una de ellas sensible a una escala espacial y orientación.
Cada unidad, al ser (máximamente) sensible a una orientación, es a su vez (máximamente) sensible a la dirección del movimiento perpendicular a dicha orientación. Esto se debe al denominado problema de la apertura (Wallach, 1976). Si a un estímulo unidimensional, con orientación α1D, se le aplica un vector velocidad v2D (con módulo |ν2D| y orientación α2D) , la velocidad con la que se desplaza el estímulo, |ν1D|, es igual a |ν2D|. cos(α2D - α1D), y la dirección es siempre perpendicular a la orientación del estímulo.
La consecuencia directa del problema de la apertura es que cuando se presenta un estímulo en movimiento (al cual se le ha aplicado un vector velocidad ν2D) cada unidad codifica una dirección y velocidad diferente (distintos vectores ν1D). ¿Cómo se integran las distintas respuestas para poder determinar el vector ν2D? o, dicho de otra forma, ¿Cómo «resuelve» el SVH el problema de la apertura?.
Soluciones al problema de la apertura
Adelson y Movshon (1982) observaron que cuando un estímulo está formado por la suma de dos enrejados con diferentes orientaciones, lo que se percibe no son dos enrejados con diferente dirección del movimiento, sino que, bajo una serie de condiciones (diferencia en frecuencia espacial entre componentes menor de 1 octava; diferencia en orientación menor de 100º; igualdad de contrastes; contrastes por encima del umbral de discriminación), se puede llegar a ver un patrón estimular de cuadrados o romboides (dependiendo de la orientación de los enrejados) moviéndose en una dirección determinada. De aquí, propusieron que la codificación de la dirección se realiza en dos etapas (Adelson y Movshon, 1982; Movshon, Adelson, Gizzi y Newsome, 1985). En la primera, un estímulo es procesado por una serie de unidades (semejantes a las descritas anteriormente) que codifican el vector velocidad de cada componente espectral. En la segunda etapa se combinan las respuestas de la primera, siguiendo el modelo computacional propuesto por Fennema y Thompson (1979), obteniéndose así un único vector velocidad.
Aunque existen datos que parecen indicar que el modelo es válido (Derrington y Suero, 1991; Welch, 1989; Welch y Bowne, 1990), se han obtenido algunos en contra. Ferrera y Wilson (1987, 1990, 1991) observan que para algunos estímulo complejos (que denominan tipo I) la dirección percibida coincide con la dirección que propone el modelo de Adelson y Movshon, mientras que para otros (que denominan tipo II) la dirección percibida se desvía en, aproximadamente, 7.5° de la dirección predicha. Además, encuentran que la velocidad percibida en estos dos tipos de estímulos siempre es menor que la velocidad de un enrejado de la misma frecuencia espacial, y con velocidad igual a la predicha por el modelo. Si se compara la velocidad con un enrejado que tiene una frecuencia espacial igual a la de los nodos del estímulo complejo, y que posee la misma velocidad que la predicha por el modelo, entonces las velocidades percibidas son iguales.
Wilson, Ferrera y Yo (1992) han desarrollado un modelo alternativo, que intenta solucionar estos problemas. Se propone que, para una escala espacial y orientación, existen dos vías que actúan en paralelo. Una de ellas, semejante a la primera etapa del modelo anterior, en la que se obtienen la codificación de los vectores velocidad de cada componente espectral del estímulo. La otra vía se desarrolla en cuatro etapas: 1) filtrado del estímulo mediante un mecanismo que no es sensible al movimiento; 2) rectificación, en el que se introducen nuevos componentes espectrales; 3) filtrado, en el que sólo se mantienen los componentes espectrales introducidos en la etapa anterior; 4) codificación de los vectores velocidad de los nuevos componentes espectrales. Las salidas de las dos vías convergen en una última etapa en el que se calcula el vector suma mediante una red neuronal. Este vector suma es el que el sistema visual asigna al estimulo en movimiento.
A pesar de que existen datos empíricos que concuerdan con las predicciones hechas por el modelo (Ferrera y Wilson, 1987, 1990, 1991; Wilson y Kim, 1994), éste presenta dos problemas: 1) no hay una evidencia experimental concluyente sobre el tipo de rectificación que habría que incluir: cada tipo de rectificación implicaría añadir distintos componentes espectrales, por lo tanto se obtendría información diferente en función del tipo elegido; 2) hasta la fecha no se tiene ninguna evidencia experimental psicofísica que demuestre la existencia de un filtrado posterior a la etapa de rectificación.
Por otra parte, a pesar de las diferencias que hay entre el modelo de Adelson y Movshon y el de Wilson et al., ambos defienden una misma idea: la existencia de un proceso jerárquico, dos etapas fundamentales para la codificación del vector velocidad de los estímulos. En una primera se obtienen la codificación de vectores velocidad parciales, en la cual no existe posibilidad de que se obtenga directamente el vector velocidad de los estímulos. En la segunda etapa se utiliza las respuestas de la primera para determinar la dirección y velocidad de los estímulos.
Algunos datos experimentales obtenidos invitan a pensar que no es necesario mantener esta estructura. En un experimento de adaptación Adelson y Movshon (1981) observaron que el estímulo adaptador (enrejado vertical) no afectaba a la percepción del estímulo test (suma de dos enrejados orientados), cuando ambos poseían la misma frecuencia espacial. Ahora bien, analizando los resultados con detalle, se observa que a medida que la frecuencia espacial del estímulo adaptador se aproximaba a la frecuencia espacial de los nodos del estímulo test se producía un incremento en el nivel de adaptación. Por otra parte, los trabajos de Ferrera y Wilson mencionados anteriormente permiten concluir que los mecanismos que procesan los estímulos complejos (suma de dos enrejados sinusoidales) y los estímulos sensibles a frecuencias espaciales bajas parecen ser mecanismos que poseen las mismas características. Estos resultados permiten hipotetizar que los componentes de los estímulos complejos pueden estar siendo procesados por un mismo mecanismo.
Una solución alternativa al problema de la apertura
Cuando se presenta la suma de dos enrejados sinusoidales en movimiento pueden existir varias respuestas con una magnitud semejante. Supongamos que presentamos la suma de dos enrejados, uno con orientación αA grados y otro con orientación αB grados; supónganse que se les ha aplicado un vector velocidad con orientación de α2D y una magnitud de |ν2D|. De esta forma, el primer enrejado tendría una velocidad igual a |ν2D|. cos(αA - α2D) y el segundo una velocidad de |ν2D|. cos(αB - α2D). En principio, cabría esperar dos respuestas máximas; una para unidades centradas en una orientación de αA grados y frecuencia similar a la del enrejado, la otra la darían unidades centradas en una orientación de αB y frecuencia similar a la del enrejado.
Ahora bien, pueden existir unidades que responda a la suma de los dos enrejados. Éstas podrían ser unidades centradas en una orientación igual a α2D. La frecuencia espacial a la que serían sensible no es la misma que las de los dos enrejados sinusoidales ya que, tal como dijimos en el apartado anterior, en un experimento de adaptación donde las frecuencias espaciales del estímulo adaptador y la del estímulo test son iguales no se obtenían niveles de adaptación apreciables. Pero sí pueden darse en unidades que son (máximamente) sensibles a una frecuencia espacial que esté próxima a la frecuencia espacial que presentan los nodos resultantes de sumar los dos enrejados.
Por lo tanto, ante un mismo estímulo pueden existir tres respuestas, una por cada tipo de unidad. Se puede suponer una interacción entre las tres respuestas; se mantiene aquella respuesta que sea máxima, eliminándose aquellas respuestas que tengan un valor más bajo (Welch y Bowne, 1990). En el caso de que existan dos respuestas con magnitudes iguales y superiores a la restante, se mantendrían las dos primeras, anulándose la última. Con este supuesto se vería recogida la posibilidad de percepción de transparencias (dos enrejados moviéndose con diferentes direcciones) descrita por Adelson y Movshon (1982).
Así, en el caso de que las respuestas de las unidades centradas en una orientación α2D y frecuencia espacial próxima a la de los nodos del estímulo complejo fuera superior a las otras dos respuestas, se percibiría un patrón complejo de cuadrados o romboides en movimiento. En el caso contrario, que las otras dos respuestas fueran mayores, se percibirían dos enrejados orientados superpuestos con diferentes direcciones.
Resumiendo, lo que propone la solución alternativa es que las mismas unidades que codifican los vectores velocidad parciales ν1D de los estímulo en movimiento también podrían responder al vector velocidad ν2D. Además, en el mismo nivel de procesamiento, se produce una interacción de las distintas respuestas que determina la respuesta final.
A continuación se va a presentar un experimento que permite evaluar si esta solución alternativa es factible. El estímulo utilizado se ha diseñado de tal forma que la percepción de éste predicha por los modelos de Adelson y Movshon y de Wilson et al. son iguales entre sí, pero diferentes a la predicción de la solución alternativa.
Experimento
Un estímulo que se corresponde a la suma de dos enrejados sinusoidales en movimiento que poseen la misma frecuencia espacial pero diferente orientación se expresa analíticamente como:
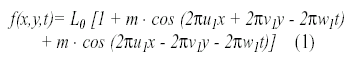
donde u1 y v1 son, respectivamente, el componente horizontal y el componente vertical de la frecuencia espacial (medida en c/º), w1 es la frecuencia temporal (medida en c/seg.), L0 es la luminancia media y m el contraste (definido como [Lmáx.-Lmín.]/2L0 , siendo Lmáx. y Lmín. luminancia máxima y luminancia mínima respectivamente).
Este estímulo producirá una percepción de cuadrados moviéndose en sentido horizontal. A este estímulo le podemos añadir dos componentes sinusoidales verticales en movimiento, que poseen la misma frecuencia espacial u1 y con direcciones puestas, quedando:
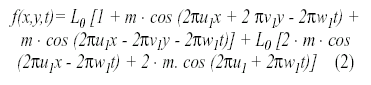
Obsérvese que los nuevos componentes no presentan información de dirección del movimiento. Al tener la misma frecuencia espacial y dirección del movimiento opuesta sólo introducen parpadeo de la luminancia en el estímulo original.
¿Qué tipo de percepción producirá un estímulo de este tipo? Según los modelos propuesto por Adelson y Movshon y por Wilson et al. los enrejados orientados son procesados por unidades distintas, donde cada una de ellas obtendría el vector velocidad correspondiente. Los enrejados verticales, procesados por las mismas unidades sensibles a una orientación de 0°, al tener direcciones opuestas hacen que dichas unidades codifiquen un vector velocidad nulo. En la segunda etapa de procesamiento sólo existen dos vectores velocidad, uno por cada enrejado orientado. El vector velocidad que le asignará la segunda etapa al estímulo es igual a la que le asignaría si no estuvieran los componentes verticales. Según los dos modelos, se percibirá un patrón de cuadrados moviéndose en sentido horizontal y con un cierto parpadeo en la luminancia del estímulo. En resumen, los dos modelos mantendrían que añadir los dos componentes verticales no produce ningún efecto sobre la percepción de la dirección del estímulo original.
La solución alternativa predeciría una percepción totalmente diferente. Atendiendo a una igualdad trigonométrica simple, la ecuación 2 se puede expresar como:
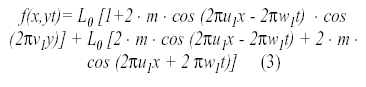
que se puede interpretar como la suma de tres enrejados sinusoidales verticales de la misma frecuencia espacial, dos de ellos poseen dirección del movimiento a la derecha y el restante, dirección a la izquierda. Uno de los enrejados con dirección derecha está modulado por un coseno horizontal.
La frecuencia horizontal u1 es equivalente a la frecuencia espacial de los nodos de un estimulo igual al expresado en la ecuación 1. Supongamos que todos los sumandos del estímulo son procesados por unidades que están centrados en una orientación 0° y (máximamente) sensibles a una frecuencia espacial igual o próxima a u1, tal y como plantea la solución alternativa. Las respuestas de estas unidades van a depender de la posición en la que se encuentren dichas unidades, más concretamente, van a depender de los valores de y. En la ecuación 3 vemos que las variaciones verticales de luminancia dependen del valor del cos(2πv1y). Dado que la función que contiene a y es periódica se puede deducir que: 1) para valores de y que se encuentran en el intervalo (2np-1)/(4v1), (2np+1)/(4v1)) (donde np=…, -2, 0, 2,…) se produce suma de cosenos tendiéndose a percibir dirección derecha; 2) para valores de y que se encuentran en el intervalo ((2ni-1)/(4v1), (2ni+1)/(4v1)) (donde ni=…, -3, -1, 1, 3,…) se produce una resta de cosenos, tendiéndose a percibir dirección izquierda. Por lo tanto, la solución alternativa predice que se van percibir bandas horizontales con dirección derecha alternándose con bandas horizontales con dirección izquierda.
Como puede observarse, ante un mismo patrón estimular las predicciones de los dos modelos y de la solución alternativa son totalmente diferentes. Para los dos primeros todos los puntos del estímulo tienen la misma dirección, para la solución alternativa la dirección del estímulo cambia de forma periódica en función de las coordenadas espaciales.
Se va a realizar un experimento que ponga a prueba las predicciones que hacen los dos modelos utilizando un estímulo semejante al definido en la ecuación 2. Este tipo de experimento es similar a uno de enmascaramiento. Se puede considerar la suma de los enrejados orientados como el estímulo test, mientras que la suma de los enrejados verticales sería el estímulo enmascarador. Se va a tomar como variable independiente la frecuencia espacial del estímulo enmascarador. En el caso de que el modelo de Adelson y Movshon o el de Wilson et al. explicaran la percepción del estimulo test como un todo, los distintos valores de la frecuencia espacial que toma el estímulo enmascarador no van a afectar a la percepción de dicho estímulo. En el caso de que la solución alternativa sea válida se tiene que cumplir que, a medida que la frecuencia espacial del estímulo enmascarador se aproxima a la frecuencia de los nodos que forman el estímulo test, el efecto de percibir bandas alternativas con direcciones opuestas tiene que ser mayor.
Método
Estímulos
Los estímulos en movimiento se han creado siguiendo la técnica propuesta por Mulligan y Stone (1989). La distancia de los sujetos al estímulo fue de 250 cm.
Para limitar el tiempo de presentación de los estímulos se utilizó una ventana temporal tipo Hanning, que modula a las funciones sinusoidales temporales. Los estímulos están limitados espacialmente mediante una ventana circular tipo Hanning (Dudgeon y Mercereau, 1984). Dos han sido los motivos para elegir este tipo de ventana: a) los componentes espectrales que introducen las ventanas circulares tipo Hanning tienen amplitudes más bajas que las que introduce una venta circular normal; b) se sabe que las ventanas espaciales pueden cambiar la percepción de la dirección de enrejados en movimiento cuando en la configuración de éstas existen elongaciones; frente a la percepción de la dirección perpendicular a la orientación del enrejado cuando éste tienen extensión infinita, se puede pasar a percibir movimiento vertical cuando es presentado dentro de una ventana rectangular vertical. Ahora bien, si en la ventana no existen elongaciones, como es el caso de la ventana circular, la percepción de la dirección del enrejado no se ve influido por la ventana; un enrejado oblicuo en movimiento se percibe con la misma dirección tanto cuando no está limitado espacialmente como cuando es presentado dentro de una ventana circula, en ambos casos se percibe dirección perpendicular a la orientación (Vallortigara y Bressan, 1991).
Los valores en frecuencia espacial para los componentes del estímulo test eran de 1c/°, 4c/°, 16c/°. La orientación de uno de ellos fue de 60°, para el otro fue de -60°. La frecuencia temporal fue siempre de 2c/seg. para todas las frecuencias espaciales. El contraste para todas las frecuencias espaciales fue de 0.033. Para todas las frecuencias espaciales, el estímulo enmascarador fue siempre la suma de dos enrejados sinusoidales verticales. El contraste de cada una de ellas fue de 0.066. La duración del estímulo fue igual a 1 segundo.
Cuando el estímulo test tenía una frecuencia espacial de 1c/° el estímulo enmascarador tomaba las siguientes frecuencias espaciales y temporales: a) 0.5c/° y 2c/seg.; b) 0.707c/° y 2.828c/seg.; c) 1c/° y 4c/seg.; d) 1.414c/° y 5.656c/seg. La velocidad del estímulo test total fue de 4°/seg. Para el estímulo test de 4c/° los valores fueron: a) 2c/° y 2c/seg.; b) 2.828c/° y 2.828c/seg.; c) 4c/° y 4c/seg.; d) 5.65c/° y 5.65c/seg. La velocidad del estímulo test total fue de 1°/seg. Por último, para el estímulo test de 16c/° los valores fueron: a) 8c/° y 2c/seg.; b) 11.3137c/° y 2.828c/seg.; c) 16c/° y 4c/seg.; d) 22.624c/° y 5.65c/seg.. La velocidad del estímulo test fue de 0.25°/seg. Obsérvese que las frecuencias temporales escogidas para los distintos estímulos enmascaradores producen una velocidad que es igual a la velocidad del patrón complejo.
Aparatos
Tanto la creación y presentación de los estímulos, como el control del experimento fue realizada por un ordenador Cyber 910.500. Las imágenes se presentaron en el monitor del propio ordenador, que tenía las siguientes características: monitor color de 19’’ con una resolución de 1248x1024 píxeles. Los programas que permiten generar y presentar las imágenes, así como controlar el experimentos fueron creados por el autor.
Los sujetos daban las respuestas pulsando, con su mano dominante, los botones de un ratón conectado al ordenador.
Procedimiento
Antes de pasar a la fase experimental se presentaron a los sujetos los estímulos test sin sumarles los estímulos enmascaradores, para comprobar que percibían un patrón de cuadrados desplazándose a la derecha y no la superposición de dos enrejados moviéndose en diferentes direcciones. En todos los casos los sujetos percibían una serie de cuadrados moviéndose en sentido horizontal.
Para cada sujeto el experimento transcurría a lo largo de tres días, uno por cada frecuencia espacial del estímulo test. La frecuencia espacial se elegía al azar. Cada sesión diaria se dividía en cinco bloques. En cada ensayo de cada bloque se presentaba el estímulo test con uno de los cuatro estímulos enmascaradores, elegido al azar. Éste no se volvía a presentar hasta que no se hubieron presentado el resto de las máscaras sumadas al test. En cada bloque y para cada par test+máscara se tomaron 25 medidas, por lo tanto en cada bloque se tomaban 100 medidas. Entre bloque y bloque se dejaba transcurrir algún tiempo para que el sujeto pudiera descansar.
El paradigma experimental fue el de elección forzada con una alternativa temporal. Se le presentaba al sujeto un par test+máscara y tenía que responder, presionando los botones de un ratón. El sujeto tenía que decidir si en el estímulo presentado existían una serie de franjas horizontales contiguas con direcciones del movimiento opuestas (izquierda-derecha), o bien si existía una única dirección del movimiento (derecha) en el estímulo.
Sujetos
Participaron dos sujetos varones, que eran ajenos a la investigación y a sus objetivos. Uno de ellos tenía visión normal (sujeto JSS), el otro (sujeto JLE) tenía visión corregida.
Resultados
En la figura 1 se presentan los resultados para los tres valores de frecuencia espacial que puede tomar el estímulo test. Se puede observar, en todos los casos, que el máximo porcentaje de respuestas se encuentra en el valor de frecuencia espacial que es igual a la frecuencia espacial de los nodos que aparecen en el estímulo test. Así, cuando el estímulo test está compuesto por dos enrejados que tienen una frecuencia espacial de 1c/° (la frecuencia de los nodos es de 0.5c/°) el efecto de percibir dos direcciones opuestas en la imagen es máximo cuando la frecuencia espacial del estímulo máscara es igual a 0.5c/°. Para una frecuencia espacial del estímulo test de 4c/° (frecuencia espacial de los nodos de 2c/°) se obtiene un porcentaje máximo cuando el estímulo máscara tiene un valor en frecuencia espacial de 2c/°. Cuando la frecuencia espacial de los componentes del estímulo test era de 16c/° (frecuencia de los nodos de 8c/°) el porcentaje máximo se obtenía cuando el estímulo máscara estaba definido por una frecuencia espacial de 8c/°. Todos estos porcentajes estaban por encima del 85%.
Por otro lado, si la frecuencia espacial del estímulo máscara era igual o superior a la frecuencia espacial de los componentes del estímulo test los sujetos tienden a ver una sola dirección, la del estímulo test sin máscara. De aquí que los porcentajes que aparecen en las diferentes figuras son muy bajos. Llegan a ser nulos cuando la frecuencia espacial de los componentes es igual a 1c/° y 16c/° en el sujeto JSS, también es nulo para las frecuencias espaciales 1c/° y 4c/° en el sujeto JLE. En el resto de las frecuencias los porcentajes fueron inferiores a un 5%.
Estos mismos resultados se presentan, de una forma más compacta, en la figura 2. En el eje de ordenadas se presenta el porcentaje de veces que los sujetos percibían bandas con direcciones opuestas. En el eje de abscisas se representa la distancia, en octavas, que existe entre la frecuencia espacial del estímulo máscara con mayor porcentaje y cada una de las frecuencias espaciales del resto de las máscaras. Teniendo en cuenta que la máscara con mayor porcentaje tiene una frecuencia espacial igual a la de los nodos del estímulo test, se observa que cuando aumenta la diferencia, en frecuencia espacial, de la máscara en relación a la frecuencia espacial de los nodos del estímulo test, el efecto de las máscaras sobre el test disminuye. Es importante hacer notar que existe una diferencia de una octava entre la frecuencia espacial de los nodos del test y la frecuencia espacial de las máscaras que no afectan a la percepción de la dirección del estímulo test. Este resultado, como veremos en el siguiente apartado, apoya la solución alternativa al problema de la apertura.
La solución alternativa propuesta permite predecir en que posiciones del estímulo aparecen las distintas franjas con direcciones opuestas. Una vez terminado el experimento se les mostraba a los sujetos el par test+máscara que tenía el porcentaje más alto de percepción de dos direcciones. Manteniendo el estímulo, se pidió a los sujetos que indicasen qué franjas tenían dirección derecha y cuáles dirección izquierda. La posición de estas franjas coincidía con los intervalos definidos anteriormente.
Discusión
Tanto el modelo de Adelson y Movshon como el de Wilson et al. permiten explicar los resultados obtenidos para frecuencias espaciales de la máscara iguales o superiores a la frecuencia espacial de los componentes del test, ya que no se produce ningún tipo de interferencia entre éstos últimos y el primero. En la primera etapa de procesamiento sólo se codifican los vectores velocidad de los componentes que tienen una orientación de 60º, mientras que la respuesta será nula para los componentes con orientación 0º. Así, en la segunda etapa de procesamiento sólo existen dos vectores velocidad, que permiten obtener una dirección del movimiento hacia la derecha. Cuando se preguntaba a los sujetos sobre la percepción que tenían en estas situaciones decían que habían visto un patrón de cuadrados moviéndose a la derecha en el que existía un pequeño parpadeo; el parpadeo percibido surgiría de las variaciones espacio-temporales del estímulo máscara.
Estos mismos modelos no son capaces de explicar los resultados cuando la frecuencia espacial del estímulo máscara es inferior a la de los componentes del test, y esto por dos razones. En primer lugar, los efectos son máximos cuando entre la frecuencia espacial de la máscara y del test existe una diferencia de una octava. Según ambos modelos, en la segunda etapa sólo se relacionarían componentes que están dentro de un mismo rango de frecuencias espaciales, siendo éste aproximadamente igual a una octava. Se podría admitir que se relacionan componentes que difieren en una octava o más (Smith, 1992) y, por lo tanto, en la segunda etapa de procesamiento intervendrían tanto los componentes del test como los de la máscara. Ahora bien, y esta es la segunda razón, el vector velocidad de la máscara es nulo y, por tanto, no afectaría a la obtención de la dirección final del estímulo. Pero como indican los resultados, la percepción de la dirección se ve afectada por la presencia de la máscara. Por lo tanto ni el modelo de Adelson y Movshon ni el de Wilson et al. permitirían explicar los resultados obtenidos.
Suponer que se procesan los estímulos en una misma etapa, pero mediante unidades que son sensibles a una frecuencia espacial distinta (en este caso inferior) que la que poseen los componentes del test (solución alternativa al problema de la apertura), permitiría tener un marco de explicación para los resultados obtenidos. Cuando el estímulo máscara tiene una frecuencia espacial igual o superior al test, el patrón complejo (test+máscara) es procesado por dos unidades diferentes: una sensible a la frecuencia espacial de la máscara, otra sensible a una escala espacial inferior (una octava menor) que procesa el test, por lo tanto no existirá interferencia. Pero cuando la máscara tiene una frecuencia menor puede llegar a ser procesada por las mismas unidades que se encargan del estímulo test, produciéndose fenómenos de enmascaramiento en la dirección. Este tipo de enmascaramiento dependería de la posición espacial en la que se encuentre la unidad. Las unidades cuya posición en el plano de la imagen vienen definidas por los valores de y pertenecientes al intervalo ((2np-1)/(4v1), (2np+1)/(4v1)) responden dirección derecha, mientras que aquellas situadas en los valores de y que pertenecen al intervalo ((2ni-1)/(4v1), (2ni+1)/(4v1)) responden dirección izquierda.
Apoyando la solución alternativa está el hecho de que las unidades sensibles al movimiento poseen un ancho de banda en frecuencia espacial en torno a 1 ó 1,5 octavas (Anderson y Burr, 1989). Si el estímulo está siendo procesado por unidades centradas en una frecuencia espacial igual a la de los nodos del test entonces, cuando las máscaras tienen una diferencia igual o superior a 1 octava en relación a los nodos del test, no tiene que existir efecto ya que éstas son procesadas por unidades diferentes a las que procesan el estímulo test. Pero cuando los estímulos máscara tienen una diferencia inferior a 1 octava, tanto los estímulo máscara como el test son procesados por las mismas unidades y, por lo tanto, existe un efecto de las primeras sobre el estímulo test (ver figura 2).
Según se dijo anteriormente, Adelson y Movshon (1982) observan que para que se vea un patrón complejo de cuadrados (o romboides) moviéndose en una dirección determinada en lugar de dos enrejados superpuestos con direcciones diferentes, se tenían que cumplir una serie de condiciones. Mientras que podían explicar una de ellas, semejanza en frecuencia espacial, no se ha dado ninguna explicación de las otras: contraste de los componentes por encima de su umbral y una diferencia en orientación menor a 100°. Desde la solución alternativa se pueden dar algunas explicaciones acerca de estas dos últimas condiciones. Respecto al contraste, las unidades que procesan el patrón complejo pueden responder a las frecuencias espaciales de los componentes, pero la sensibilidad que posee a éstas será menor que aquellas unidades que responden a cada componente por separado. Esto se debe a que las primeras están centradas en una frecuencia espacial inferior frente a las últimas que estarían centradas en una frecuencia espacial próxima a la de los componentes. Entonces, se podría esperar una respuesta inferior de las unidades que responden al estímulo como un todo cuando los componentes estén en el umbral de contraste. En relación a la orientación, a medida que la diferencia en orientación aumenta, el estímulo complejo va ser procesado por unidades que están centradas en frecuencias espaciales más bajas y, por consiguiente, van a ser menos sensibles a las frecuencias espaciales de los componentes del estímulo complejo. De aquí es fácil comprender por qué un aumento en la orientación produce una menor sensibilidad en la percepción del estímulo complejo.
Atendiendo a los resultados de las investigaciones de Ferrera y Wilson (1987, 1990, 1991), es comprensible que los estímulos complejos tengan las mismas características perceptivas que los enrejados sinusoidales de frecuencias espaciales más bajas, ya que éste es procesado por unidades que están centradas en frecuencias espaciales inferiores.
Por último, si el procesamiento de estímulos complejos viene determinado por las mismas unidades que procesan estímulos unidimensionales, las primeras tienen que tener la misma estructura que las últimas. Esto estaría en consonancia con los resultados de las investigaciones de van den Berg y van de Grind (1991) que ponen de manifiesto que la estructura de las unidades que responden a un patrón bidimensional complejo de líneas es igual a la de un patrón unidimensional de líneas.
La solución alternativa propuesta es sólo un primer boceto de lo que tendría que ser un modelo de cómo el SVH es capaz de determinar la dirección de los distintos objetos que se mueven en la escena. El modelo completo tendría que determinar cuáles son las diferencias en respuesta de las diferentes unidades para que se pueda escoger una de ellas, o bien si hay una combinación entre ellas. Futuros trabajos permitirán conocer cuál es la relación entre las salidas y cómo se combinan.
Agradecimientos
Parte de este trabajo se realizó en el Laboratorio de Visión de la Facultad de Psicología de la Universidad Complutense de Madrid. Además, ha recibido financiación del proyecto PB96-0052 concedido por la Secretaria de Estado de Universidad, Investigación y Desarrollo (MEC).
Adelson, E.H. & Bergen, J.R. (1985). Spatiotemporal energy models for the perception of motion. Journal of the Optical Society of America A, 2, 284-299.
Adelson, E.H. & Movshon, J.A. (1981). Two kinds of adaptation to moving patterns. Invest. Ophtalmol. Vis. Sci., supp. 20, 17.
Adelson, E.H. & Movshon, J.A. (1982). Phenomenal coherence of moving visual patterns. Nature, 300, 523-525.
Anderson, S.J. & Burr, D.C. (1989). Receptive field properties of human motion detector units inferred from spatial frequency masking. Vision Research, 29, 1.343-1.358.
Anderson, S.J. & Burr, D.C. (1991). Spatial summation properties of directionally selective mechanisms in human vision. Journal of the Optical Society of America A, 8, 1.330-1.339.
Anderson, S.J., Burr, D.C. & Morrone, M.C. (1991). Two-dimensional spatial and spatial-frequency selectivity of motion-sensitive mechanisms in human vision. Journal of the Optical Society of America A, 8, 1.340-1.351.
van den Berg, A.V. & van de Grind, W.A. (1991). Conditions for the detection of coherent motion. Vision Research, 31, 1.039-1.051.
Derrington, A. & Suero, M. (1991). Motion of complex patterns is computed from the perceived motions of their components. Vision Research, 31, 139-149.
Dudgeon, D.A. & Mersereau, R.M. (1984). Multidimensional digital signal Processing. Englewood Cliffs, NJ: Prentice Hall.
Fennema, C.L. & Thompson, W.B. (1979). Velocity determination in scenes containing several moving objets. Computer Graphics and Image Processing, 9, 301-315.
Ferrera, V.P. & Wilson, H.R. (1987). Direction specific masking and the analysis of motion in two dimensions. Vision Research, 27, 1.783-1.796.
Ferrera, V.P. & Wilson, H.R. (1990). Perceived direction of moving two-dimensional patterns. Vision Research, 30, 273-287.
Ferrera, V.P. & Wilson, H.R. (1991). Perceived speed of moving two-dimensional patterns. Vision Research, 31, 877-893.
Movshon, J.A., Adelson, E.H., Gizzi, M.S. and Newsome W.T. (1985). The analysis of moving visual patterns. En C. Chagas, R. Gattass & C.G. Gross (Eds.), Pattern Recognition Systems. New York: Springer.
Mulligan, J.B. & Stone, L.S. (1989). Halftoning method for the generation of motion stimuli. Journal of the Optical Society of America A, 6, 1.217-1.227.
van Santen, J.P.H. & Sperling, G. (1985). Elaborated Reichardt detectors. Journal of the Optical Society of America A, 2, 300-321.
Smith, A.T. (1992). Coherence of plaids comprising components of disparate spatial frequencies. Vision Research, 32, 393-397.
Vallortigara, G. & Bressan, P. (1991). Occlusion and the perception of coherent motion. Vision Research, 31, 1.967-1.978.
Wallach, H. (1976). On perception. New York: Quadrangle.
Welch, L. (1989). The perception of moving plaids reveals two motion-processing stages. Nature, 337, 734-736.
Welch, L. & Bowne, S.F. (1990). Coherence determines speed discrimination. Perception, 19, 425-435.
Wilson, H.R., Ferrera, V.P. & Yo, C. (1992). Psychophysically motived model for two-dimensional motion perception. Vis. Neurosci., 9,79-97.
Wilson, H.R. & Kim, J. (1994). Perceived motion in the vector sum direction. Vision Research, 34, 1.835-1.842.
Aceptado el 15 de diciembre de 1998