Psicothema was founded in Asturias (northern Spain) in 1989, and is published jointly by the Psychology Faculty of the University of Oviedo and the Psychological Association of the Principality of Asturias (Colegio Oficial de Psicología del Principado de Asturias).
We currently publish four issues per year, which accounts for some 100 articles annually. We admit work from both the basic and applied research fields, and from all areas of Psychology, all manuscripts being anonymously reviewed prior to publication.
Psicothema, 2000. Vol. Vol. 12 (Suplem.2). 519-521
Carmen Santisteban Requena
Universidad Complutense de Madrid
En este trabajo se construye un modelo probabilístico para representar un proceso de aprendizaje en el contexto de los modelos de estado en la denominada teoría matemática del aprendizaje. El modelo incluye tanto el proceso de adquisición como el de olvido, así como el supuesto de que el proceso puede terminar en uno cualquiera de r estados. Se consideran en el modelo dos estados transitorios y un número finito r de estados absorbentes. Las transiciones se supone que están reguladas por la «fuerza de la respuesta» según la concibe Luce en su modelo b de aprendizaje y que deriva a partir de su axioma de elección.
Stochostic learning models for dichotomous response trials and a finite number of absorbing states. A probabilistic model for a learning process has been built up in the context of the state models for the learning mathematical theory. Two transitory states (for the acquisition and forgetting processes) and a finite number of absorbing states are considered. The transition probabilities are assumed to be controlled by the «response strength» of the Luce’s β model, derived from his choice axiom.
La teoría del aprendizaje ofrece una multitud de puntos de vista y de resultados al amparo de los cuales, en el proceso de formalización que ha experimentado la Psicología a lo largo del presente siglo, se han desarrollado distintos tipos de modelos, (e.g. Atkinson, Bower y Crother, 1965; Wickens, 1982; Townsed y Ashby, 1983). En este trabajo nos enmarcamos en concreto en los que en la obra de Coombs (Coombs, Daves, y Tversky, 1970) se incluyen en la «Teoría Matemática del Aprendizaje»
Los modelos mejor establecidos en la teoría matemática del aprendizaje han sido los modelos operador lineal desarrollados por Bush y Mosteller (Bush y Mosteller, 1951, 1955), también denominados modelos α, el modelo operador no lineal β de Luce, basado en el concepto de «fuerza de la respuesta», que deriva de su axioma de elección (Luce, 1959) y los modelos a los que en la obra de Coombs et al. (1970) se clasifican como «Modelos de Estado» (Estes, 1950). Entre estos últimos modelos ocupan un lugar muy relevante los modelos cuya axiomática conduce a la representación del proceso de aprendizaje como una cadena de Markov. Estos modelos no se encuentran bien establecidos hasta los años 60, en que aparecen desde representaciones muy simples, como es el modelo de un elemento en la estructura que propone Bower (Bower, 1961, 1962) o modelos con más componentes, como los que, entre otros, proponen Atkinson y Crothers (1964) o Bernbach (1965).
En el presente trabajo se considera un modelo estocástico de aprendizaje que incluye tanto el proceso de adquisición como el de olvido, que se representa como la posibilidad de paso entre dos estados recurrentes transitorios Aα y Aβ. También el modelo incluye un número r de estados absorbentes, puesto que parece razonable suponer que el sujeto puede eventualmente terminar el aprendizaje en un cierto estado Fδ.
Se considera que en el intervalo temporal (τ , t) con 0 ≤ τ ≤ ∞ el sistema puede viajar entre dos estados transitorios Aα y Aβ ( α , β = 1,2 ) y puede alcanzar uno de los finitos estados finales Fδ (δ =1, ..., r) que son absorbentes.
Las transiciones entre los estados Aα y Aβ responden a que el sujeto puede adquirir la respuesta deseada u olvidar, por lo que aumenta o disminuye el número de respuestas correctas que da el sujeto de un ensayo a otro. Estos cambios, sin embargo, no se considera que responden al modelo conocido como de «ganancia-pérdida» en el contexto de los modelos operador lineal desarrollados dentro de la teoría estocástica del aprendizaje por Bush y Mosteller en los que, al aplicar un operador, la probabilidad de respuesta correcta se modifica de forma que el nuevo valor es igual al anterior más un incremento proporcional a lo que queda por aprender (1-p) y un decremento proporcional al mismo p, es decir, a lo ya aprendido. En el presente trabajo, a pesar de que el paso entre los estados Aα y Aβ se realiza debido a la ganancia o pérdida de algún elemento, en estas transiciones no se hacen sin embargo consideraciones de proporcionalidad, como en los modelos anteriormente citados, sino que las transiciones se consideran gobernadas por las intensidades o «fuerza de la respuesta» introducida por Luce en el modelo β en el sentido que él mismo da a la escala que se deriva directamente de su axioma de elección (Luce, 1959).
Todas las transiciones entre estados se suponen que están gobernadas por las fuerzas de las respuestas. A estas fuerzas los denominamos ναβ cuando los transiciones son entre los estados Aα y Aβ y las denominamos μαδ cuando el paso se realiza entre cualquiera de los estados A y uno de los estados F.
El modelo que se presenta formaliza estas relaciones, que responden inicialmente a una versión de las ecuaciones de Chapman-Kolmogorov en un proceso estocástico. Se dan las soluciones de las ecuaciones diferenciales para el cálculo de las probabilidades de transición Pαα , Pαβ y Qαδ y se determinan las constantes en función de las condiciones iniciales que se establecen y de las raíces características de las ecuaciones.
Supuestos
Supuesto 1: El proceso de aprendizaje es potencialmente concurrente, repetitivo y reversible, mientras que el estado final es un proceso irreversible o absorbente
Supuesto 2: Se consideran dos estados transitorios Aα y Aβ y un número finito r de posibles estados finales Fδ . (α, β = 1, 2; δ = 1,2,..., r)
Supuesto 3: En el intervalo ( τ , t) con 0 ≤ τ ≤ t < ∞ el sujeto puede viajar continuamente entre los dos estados Aα y Aβ y puede alcanzar alguno de los estados finales Fδ.
Supuesto 4: Las transiciones están gobernadas por las intensidades o fuerza de la respuesta que son respectivamente ναβ y μαδ , y que representan genéricamente las intensidades de los sucesos asociados a los estados Aα y Aβ y los asociados de los sucesos de los estados Fδ.
Supuesto 5: Las intensidades ναβ y μαδ se supone que son independientes del instante ξ, (τ ≤ ξ ≤ t) en el que está el sistema en el intervalo (τ , t) en el que se produce el cambio.
Probabilidades de paso y condiciones iniciales
La probabilidad de paso entre los estados Aα y Aβ en el intervalo Δ(t) es:
Pαβ = ναβ Δ(t) + C [Δ(t)] ; α ≠ β
siendo C[Δ(t)] la probabilidad de más de un cambio en ese intervalo temporal.
La probabilidad de pasar a uno de los estados finales en un intervalo Δt es:
Pαδ = μαδ Δ (t) + C [ Δ (t) ]
La probabilidad de transición a un estado final permanente Qαδ se obtiene considerando que se puede hacer directamente desde Aα o bien a través de Aβ (α ≠ β).
Se considera que
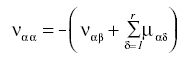
y que ναβ > 0 (así como νβα) y que ναα ≠ 0 , pues en el caso en que ναα = 0 el estado Aα será absorbente. Se supone además que
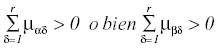
Condiciones iniciales
Las probabilidades de transición Pαβ ( τ , t ) y Pαδ ( τ, t ) satisfacen las condiciones iniciales siguientes:
i) Pαα(τ,τ) = 1 ; α = 1, 2
ii) Pαβ (τ,τ) = 0 ; α ≠ β ; α,β = 1,2
iii) Pαδ (τ,τ) = 0 ; α = 1, 2 ; δ= 1,2,..., r
El modelo
Para un individuo en Aα en un instante cualquiera ξ del intervalo (τ, t)
Pαβ( τ, ξ ) . Pβγ (ξ,t) ≡ Pβγ = Pr {estar en Aβ en ξ y en Aγ en t}
Ya que los anteriores sucesos son mutuamente excluyentes para diferentes β:
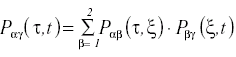
que es una versión de la ecuación de Chapman-Kolmogorov.
Por lo tanto:
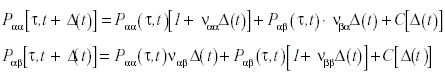
Formando los cocientes diferenciales y tomando límites para Δ ( τ ) → 0 , se obtiene que:
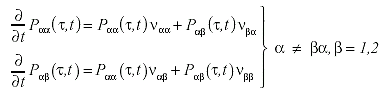 (I)
(I)
Las soluciones de ese sistema de ecuaciones diferenciales homogéneas con coeficientes constantes es de la forma:
![]() (II)
(II)
donde s es una función de las fuerzas de respuesta.
Sustituyendo (II) en las ecuaciones diferenciales, éstas toman la forma:
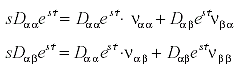
Es fácil comprobar que hay dos raíces características s1 y s2 que son los únicos valores reales de s para que las expresiones (II) puedan ser soluciones de las ecuaciones (I). Además, al considerarse ναβ > 0 y νβα > 0 las raíces serán distintas.
La solución general es:
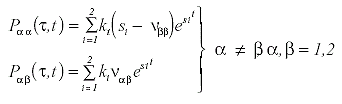 (III)
(III)
Los dos coeficientes D para cada raíz si se denotan por Dααi y Dαβ i y la relación entre los coeficientes y las constantes ki es:
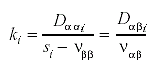
teniéndose para cada si un par de soluciones de las ecuaciones (III).
Para la determinación de las constantes se hace uso de las condiciones iniciales y haciendo τ = t en (III) se tiene que:
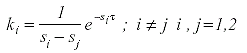
Por lo tanto las Probabilidades de Transición entre estados de aprendizaje son:
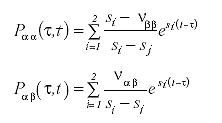 (IV)
(IV)
que no depende de t o de τ , sino de ( t - τ ). Es decir, el proceso es homogéneo respecto al tiempo.
Las Probabilidades de Transición a un estado final permanente Qαδ (t) se obtienen considerando que el individuo puede alcanzar uno de esos estados Fδ directamente desde Aα , o bien a través de Aβ ; α ≠ β.
Considerando un intervalo infinitesimal ( τ , τ + dτ ), para τ fijo ( 0 < τ ≤ t ), la probabilidad de estar en Aα y alcanzar un estado Fδ es igual a:
![]() (V)
(V)
Sustituyendo Pαα ( τ , t ) y Pαβ ( τ , t ) en la ecuación (V) e integrando se obtiene:
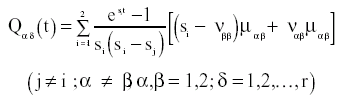
Conclusiones
Este trabajo formaliza un modelo de aprendizaje en el que se contemplan el proceso de adquisición y el de olvido, así como la posibilidad de que el sujeto finalice el aprendizaje en uno cualquiera de r estados. Se supone que el sujeto puede viajar entre dos estados de aprendizaje recurrentes transitorios y que en cualquier momento puede pasar a un estado final que es absorbente.
En el trabajo se explicitan como se pueden calcular las probabilidades de paso entre esos dos estados transitorios, así como las de paso a uno de los estados finales considerados a priori irreversibles. Las soluciones se dan bajo los supuestos, nunca anteriormente contemplados en este tipo de modelos, de que las transiciones están gobernadas por la «fuerza de la respuesta», de acuerdo con el axioma de elección de Luce y que la consideración de «ganancia-pérdida» en el aprendizaje, incluida en este modelo, también se supone que está gobernada por la fuerza de la respuesta y no por los supuestos de proporcionalidad entre lo aprendido y lo que queda por aprender, como se hace en los modelos de Bush y Mosteller.
Se pueden considerar como casos particulares de este modelo, los correspondientes a un proceso puro de adquisición o uno puro de extinción de una respuesta.
Agradecimientos
Este trabajo está parcialmente financiado por el Ministerio de Educación y Cultura, proyecto BIO97-0543 y por la Universidad Complutense de Madrid proyecto PR156/97-7193.
Atkinson, R.C. y Crothers, E.J (1964). A comparison of paired associate learning models having different acquisition and retention axioms. Journal of Mathematical Psychology 1, 285-315
Atkinson, R.C.; Bower, G.H. y Crothers, E.J. (1965). An introduction to mathematical learning theory. New York. Wiley.
Bernbach, H.A. (1965). A forgetting model for paired associate learning. Journal of Mathematical Psychology, 2, 128-144.
Bower, G.H. (1961). Application of a model to paired-associate learning. Psychometrika, 26, 255-280.
Bower, G.H. (1962). A model for response and training variables in paired-associate learning. Psychological Review, 69, 34-53.
Bush, R.R. y Mosteller, F. (1951). A mathematical model for simple learning. Psychological Review.58, 313-23
Bush, R.R. y Mosteller, F. (1955). Stochastics Models for Learning. New York. John Wiley & sons, Inc. London, Chapman & Hall, Limited.
Coombs, C.H; Dawes, R.M. y Tversky, A. (1970). Mathematical Psychology. Prentice - Hall Series in Mathematical Psychology. New Jersey. Prentice Hall.
Luce, R.D. (1959). Individual choice behavior. New York. Wiley.
Santisteban, C. (1998). Modelos de Aprendizaje. Madrid. Ed. DMCC
Townsed, J.T. y Ashby, F.G. (1983). Stochastic modeling of elementary psychological processes. Cambridge University Press.
Wickens, T.D. (1982). Models for behavior: Stocastic Processes in Psychology. San Francisco. Freeman and company ed.