Psicothema was founded in Asturias (northern Spain) in 1989, and is published jointly by the Psychology Faculty of the University of Oviedo and the Psychological Association of the Principality of Asturias (Colegio Oficial de Psicología del Principado de Asturias).
We currently publish four issues per year, which accounts for some 100 articles annually. We admit work from both the basic and applied research fields, and from all areas of Psychology, all manuscripts being anonymously reviewed prior to publication.
Psicothema, 1992. Vol. Vol. 4 (nº 1). 261-267
Esther Torres y Marcelino Cuesta
Euskal Herriko Unibertsitatea. Universidad de Oviedo
Este trabajo presenta una revisión de las propiedades psicométricas del Test de Matrices Progresivas de Rayen (Escala Superior), empleando para ello una muestra de 1028 sujetos estudiantes de primer curso de la Universidad del País Vasco/Euskal Herriko Unibersitatea. Los análisis realizados se llevan a cabo tanto desde la perspectiva clásica (fiabilidad, dificultad, discriminación) como desde la Teoría de Respuesta a los Items (función de información, curva característica del test parametros a y b). Según los resultados obtenidos, cabe destacar la facilidad de la prueba para el tipo de sujetos empleados y la poca información que aporta para niveles medios y altos de la variable medida.
Palabras Clave: Test de Raven, Teoría de Respuesta a los Items, Modelos Logísticos, Función de Información.
Psychometria properties of the Raven progressive matrices test. This paper presents a review of the psychometric properties of Raven s Progressive Matrices test (superior level) using a sample of 1028 freshman from the University of Pais Vasco/Euskal Herriko Unibersitatea. The analyses were carried out from the Classical Test Theory perspective (reliability, dificulty, discrimation) and from the Item Response Theory point of view (information function, test characteristic curve, parameter a and b). The results show the easiness of this test for the kind of subjects used here, and the poor information provided for middle and superior values of the Θ scale.
Key words: Raven Test, Item Response Theory, Logistic Models, Information Function.
En este trabajo se lleva a cabo un análisis psicométrico de uno de los tests más clásicos y de más amplia utilización en la medida de la Inteligencia General, el Test de Matrices Progresivas de Raven. Si bien las características psicométricas de esta prueba están bien documentadas, lo "veterano" de la edición española así como los resultados encontrados por Cuesta, Muñiz y Paz (en prensa) al emplear la Teoría de Respuesta a los Items (TRI) en un trabajo similar al que aquí se presenta, hacen pensar en lo conveniente de llevar cabo una revisión de sus propiedades. El presente trabajo se centra principalmente en el análisis de items aplicando para ello los modelos de TRI. El objetivo es conocer los índices de dificultad, discriminación y la función de información de los items, además de descubrir como cada uno de los items del Raven contribuyen a la medida de la Inteligencia General. Para ello contamos con una muestra amplia de 1028 sujetos, estudiantes de la Universidad del Pais Vasco/E.H.U., de manera que podamos tener una cierta seguridad en la estimación de los parámetros, y de forma especial el parámetro de discriminación. (Baker, 1987; Lord, 1986).
Los análisis se realizan desde un punto de vista clásico (Gulliksen, 1950; Lord y Novick, 1968; Crocker y Algina, 1986) y también desde el punto de vista de la TRI, que como es bien sabido aporta ciertas alternativas a algunos problemas que la Teoría Clásica de los Tests (TCT) no podía abordar (Lord, 1980; Hambleton y Swaminathan, 1985; Goldstein y Wood, 1989; Muñiz, 1990; Muñiz y Hambleton, en prensa).
METODO
Muestra
Participaron 1.028 sujetos de los cuales 542 eran hombres y 486 mujeres. Sus edades estaban comprendidas entre 17 y 42 años, con una media de 18,95 años. Todos los sujetos eran estudiantes de primer curso universitario pertenecientes al Campus de Gipuzkoa de la Universidad del Pais Vasco/Euskal Herriko Unibertsitatea durante el curso académico 1989/1990. La distribución de la muestra por centros fue como sigue: 152 sujetos de la Facultad de Derecho, 232 de la Escuela Técnica Superior de Ingenieros Industriales, 251 de la Facultad de Informática, 132 de la Facultad de Psicología, 40 de la Facultad de Filosofía y Ciencias de la Educación, 78 de la Escuela de E.G.B. y 143 de la Escuela Universitaria de Estudios Empresariales.
Instrumento
Test de Matrices Progresivas de Raven, versión de 1962 y editado por Mepsa en 1970. Esta versión consta de dos series, la serie I compuesta por 12 items y la serie II por 36.
Procedimiento
La aplicación del test se realizó durante el primer trimestre de 1990 en los respectivos centros, necesitándose varios días para finalizar la administración. La participación de los sujetos fue voluntaria. La prueba se realizó siguiendo las instrucciones del manual y respetando el tiempo de aplicación propuesto en el manual (40 minutos).
Análisis de Datos
En la realización de los análisis se emplearon dos paquetes de ordenador: SPSS /PC+, para los análisis clásicos, y PC-BILOG (Mislevy y Bock, 1986), para los análisis específicos de TRI.
Razones teóricas hacían suponer que dadas las características de la prueba que nos ocupa el modelo logístico más apropiado sería el de dos parámetros, pues con seis alternativas de respuesta por item parece razonable esperar que el azar juegue un papel poco importante y por tanto c= 0. Por otro lado los índices de discriminación clásicos diferentes permiten desechar el modelo de un parámetro. Efectivamente, tras comprobación empírica del ajuste de los modelos de uno, dos y tres parámetros, el modelo logístico que mejor ajusta a nuestros datos es el de dos parámetros (.χ2 = 266.9, p ≤ 0.6728). Sólo dos de los cuarenta y ocho items que componen el test no ajustan a dicho modelo, son los items 11 y 12.RESULTADOS
Indices de dificultad y discriminación de los items
En la Tabla 1 se pueden observar los indices de dificultad y de discriminación tanto desde el punto de vista de la TCT como desde la TRI. Se observa la coincidencia de ambos tipos de índices en cuanto a las conclusiones a las que apuntan, el test resulta muy fácil y poco discriminativo para el tipo de sujetos que componen la muestra en la que trabajamos.
Ahondando un poco más en lo que acabamos de apuntar más arriba, señalar que la media del parámetro b (dificultad) resultó ser -1.798, dándose casos extremos de items como el 1 y 2 con valores para b de -7.583 y -5.083 (nótese que la escala de Θ suele representarse a lo sumo entre + 4 y - 4).
En lo que respecta al parámetro a, recordando que su rango de valores suele situarse entre 0 y 2, tomamos como referencia, aún manteniendo todas nuestras reservas hacia las etiquetaciones rígidas, la asignación realizada por Baker (1985, pag 24) a los valores de a.
Como puede verse nuestros valores del parámetro a caerían en el mejor de los casos en la categoría de moderados. Así mismo cabe destacar como los peores índices de discriminación predominan entre aquellos items cuya dificultad es algo superior, lo cual viene a reafirmar lo arriba dicho sobre la facilidad del test para nuestra muestra.
Fiabilidad y Dimensionalidad de la escala.
La fiabilidad fue estimada mediante el coeficiente Alfa (α), tomando un valor de 0,83. Como complemento a este índice de consistencia interna se calcularon otros dos indicadores derivados del análisis factorial como son la Theta (Θ) de Carmines (Carmines y Zeller, 1979) y la Omega (Ω) de Heise y Bohrnstedt (1970). Como es conocido estos coeficientes son estimadores del límite superior de α siendo su ordenación en lo referente a su cuantia como sigue α < Θ < Ω. Para los datos con los que hemos trabajado Θ alcanza un valor de 0,845 y ω de 0,91.
Tomando como criterio el buen ajuste del modelos logístico de dos parámetros a los datos (χ2 = 266,9, p ≤ 0,6728), puede considerarse que los items constituyen un constructo razonablemente unidimensional. Sin embargo, sometidos los items a un análisis factorial (PCA), la unidimensionalidad aparece como más problemática (véase gráfica 1). Ambos criterios parecen no converger estrictamente, pero son bien conocidas las limitaciones del análisis factorial con variables dicotómicas (McDonald, 1981; Hattie, 1984; Bemstein y Teng, 1989).
Curva característica del test
Cuando se trabaja en el marco de la TRI las puntuaciones de los sujetos vienen dadas en lo que conocemos como escala Θ, cuyos límites teóricos están entre + ∞ y - ∞, aunque a nivel práctico los valores entre los cuales se suele tomar van entre +3 y -3. Una manera de establecer relación entre la escala de Θ y la escala propia del test es a través de lo que conocemos como Curva Característica del Test, la cual permite la traducción de un tipo de puntuación a otra. Estas dos puntuaciones son una misma cosa pero expresada en diferentes escalas (Lord, 1980; Muñiz, 1990). La curva que expresa esta relación en nuestros datos puede observase en la siguiente gráfica.
Función de información
En general cuando nos referimos al concepto de Información en el ámbito de la estimación de parámetros, este viene definido por el inverso de la varianza de error (De Grúitjer y Van der Kamp, 1984; Hulin, Drasgow y Parsons, 1983):
![]()
En el marco de la TRI la Función de Información de un Test, I (Θ), viene dada por:
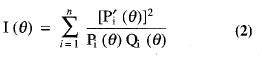
Y nos indica la información que el test aporta para los diferentes niveles de Θ, cuanta más información más precisión en la medida o lo que es lo mismo menos error de medida.
Como se ve en la expresión 2 la Función de Información del Test es la suma de las Funciones de Información de los Items. Fijándonos en los puntos de máxima información que aparecen en la tabla 1 observamos como sólo 14 (los señalados con un asterisco) de los 48 items aportan información máxima en valores medios de la escala (entre ± 1). Sin embargo, en esos puntos la cantidad de información es mínima, dándose el mayor aporte de información en los items situados en niveles más bajos de Θ.
En lo referente al test en su conjunto, en la gráfica 3 ofrecemos su Función de Información.
En concordancia con todo lo que llevamos expuesto nos encontramos con que la mayor efectividad del test que nos ocupa se da para valores de Θ aproximadamente entre -3 y -1, luego su ámbito ideal de utilización será con sujetos cuya puntuación en Θ se sitúe en esa franja.
CONCLUSIONES
A la luz de los datos que se han ido ofreciendo la conclusión más general es que el Test de Matrices Progresivas de Raven (Escala superior) aporta su máxima información para valores muy bajos de la variable inteligencia. Parece, por tanto, desaconsejable la utilización de este instrumento cuando el deseo del profesional sea discriminar entre sujetos de alta competencia.
Nótese que la utilización de técnicas procedentes del campo de la TRI no viene más que a precisar más la información que aportan los índices clásicos. Gran parte del "arsenal" tecnológico que aportan estos modelos ha sido aquí obviado (como la Función de Información de cada item, o la Curva Característica de los Items, que también nos ofrece PC-BILOG) por cuanto supondría sobrepasar los límites de lo que este trabajo pretendía. Es claro, en cualquier caso, que en la línea de otros trabajos (Cuesta el al., en prensa) también desde aquí animamos a las empresas españolas del ramo a esforzarse en la utilización del nuevo instrumental, no sólo en la actualización de tests existentes sino, y más bien, en la creación de nuevas pruebas dentro de la filosofía de los bancos de items, donde la TRI despliega realmente todo su potencial, tal y como resaltan Muñiz y Hambleton (en prensa): "Los Bancos de Items constituyen la piedra angular de la TRI, sin ellos nada de lo dicho hasta ahora se mantendría y sería aplicable".
REFERENCIAS
Baker, F.B. (1985). The basics of item response theory. Porstmouth: N. H. Heineman.
Baker, F.B. (1987). Item parameter estimation under one, two and three parameter logistic models. Applied Psychological Measurement,11, 11-141.
Bernstein,I.H. y Teng, G. (1989). Factoring items and factoring scales are different: Spurious evidence for multidimensionality due to item categorization. Psychological Bulletin, 105,467-477.
Carmines, E.G. y Zeller, R.A. (1979). Reliability and validity assessment. Londres: Sage.
Crocker, L. y Algina, J. (1986). Introduction to classical and modern test theory. New York: Holt, Rinehart and Winston.
Cuesta,M.; Muñiz, J. y Paz, M.D. (en prensa). Funciones de información y otras propiedades psicométricas de cuatro tests clásicos de inteligencia general: PMA-R, Raven, D-48 y BLS-IV. Investigaciones Psicológicas.
De Gruitjer, N.M. y Van der Kamp, L.J.T. (1984). Statistical models in psychology and educational testing. Lisse: Swets and Zeitlinger.
Goldstein, H. y Wood, R. (1989). Five decades of item response modelling. British Journal of Mathematical and Statistical Psychology, 42,139-167.
Gulliksen, H. (1950). Theory of mental tests. New York: Wiley.
Hambleton, R.K. y Swaminathan, H. (1985). Item response theory: Principles and applications. Boston: Kluwer Academic Publishers.
Hattie, J.A. (1984). An empirical study of various indices for determining unidimensionality. Multidimensional Behavioral Research,19, 49-78.
Hattie, J.A. (1985). Methodological review: Assessing unidimensionality of tests and items. Applied Psychological Measurement, 9, 139-164.
Heise, D.R. y Bohmstedt, G.W. (1970). Validity, invalidity and reliability. En E.F. Borgatten y G.W. Bohrnstedt (Eds.): Sociological Methodology. San Francisco: Jossey Bass.
Hulin, C.L.; Drasgow, F. y Parsons, C.K. (1983). Item response theory. Application to psychological measurement. Homewood, Illinois: Dow Jones-Irvin.
Lord, F.M. y Novick, M. (1968). Statistical theories of mental tests scores. Reading, MA: Addison-Wesley.
Lord, F.M. (1980). Applications of item response theory to practical testing problems. Hillsdale, NJ: LEA.
Lord, F.M. (1986). Maximum likelihood and bayesian parameter estimation in item response theory. Journal of Educational Measurement, 23(2), 157-162.
McDonald, R.P. (1981). The dimensionality of tests and items. British Journal of Mathematical and Statistical Psychology, 34, 100-117.
Mepsa (1970). Test de matrices progresivas de Raven. Escala Superior. Madrid.
Mislevy, R.J. y Bock, R.D. (1986). PC-BILOG. Moresville, IN: Scientific Software, Inc.
Muñiz, J. (1990). Teoría de respuesta a los items. Madrid: Pirámide.
Muñiz, J. y Hambleton, R.K. (en prensa). Medio siglo de teoría de respuesta a los items. Anuario de Psicología.