Psicothema was founded in Asturias (northern Spain) in 1989, and is published jointly by the Psychology Faculty of the University of Oviedo and the Psychological Association of the Principality of Asturias (Colegio Oficial de Psicología del Principado de Asturias).
We currently publish four issues per year, which accounts for some 100 articles annually. We admit work from both the basic and applied research fields, and from all areas of Psychology, all manuscripts being anonymously reviewed prior to publication.
Psicothema, 1994. Vol. Vol. 6 (nº 2). 311-317
Pere Joan Ferrando i Piera. Andreu Vigil i Colet y Urbano Lorenzo Seva
Facultat Ciencias de l'Educació i Psicologia. Universitat Rovira i Virgili.
En el presente trabajo se realiza un estudio preliminar acerca de las posibilidades de aplicación del modelo poissoniano I de Rasch (1960) en la estimación del tiempo de inspección. Asimismo se propone un método simple para verificar el ajuste. Aún con el reducido tamaño muestral utilizado, el modelo parece ser aplicable a este tipo de tareas.
Estimation of Inspection Time By Means of Poisson-1 Rasch Model. A preliminar study about Poisson-1 Rasch model adequacy to inspection time estimation is presented. A simple method to control the model data fit is also presented. In despite of little sample size, the model seems to be appropiate to this kind of tasks.
Key words: Inspection Time, Poisson processes, Item Response Fitting.
En el trabajo más conocido de Georg Rasch (1960), el matemático danés propone tres modelos probabilísticos para la calibración de escalas de rendimiento máximo. La enorme popularidad alcanzada por el tercer modelo, el denominado «logístico de un parámetro», parece haber eclipsado en cierto modo a los otros dos, basados ambos en la distribución de Poisson. Sin embargo, de acuerdo a algunas revisiones recientes (Goodstein y Wood, 1990), los denominados «modelos Poissonianos de Rasch» resultaban potencialmente incluso más interesantes que el modelo logístico, aún cuando fuesen más difíciles de encuadrar en el marco de la teoría de respuesta a los ítems (TRI).
Los modelos I y II en la monografía de Rasch estaban destinados a evaluar la capacidad lectora y, a diferencia del tercer modelo, tenían como unidad de análisis al test completo en lugar del ítem. Todos ellos, sin embargo, compartían una misma filosofía general basada en la intención de suprimir supuestos distribucionales en la población y de conseguir estimaciones invariantes, tanto de la dificultad de los instrumentos de medida, como de la habilidad de los sujetos. En este trabajo utilizaremos el primero de los dos modelos de Rasch basados en la distribución de Poisson.
Existen diversos enfoques posibles en el estudio de la distribución de Poisson (ver p. ej. Haight, 1967). Sin embargo, respecto a los modelos psicométricos que aquí se tratan, el enfoque más apropiado es el que considera a dicha distribución como el límite de la distribución binomial cuando, simultáneamente, «n» tiende a infinito y «p» tiende a cero.
En relación a una escala psicométrica, las condiciones para que se considere apropiada la ley de Poisson serían las siguientes: a) debería ser una escala formada por un número elevado de ítems dicotómicos y localmente independientes. b) La probabilidad de error debería ser la misma en todos los ítems y muy baja. En terminología psicométrica diríamos que todos los ítems deberían tener el mismo índice de dificultad (p) y que dicho índice debería tener un valor cercano a 1.
PRINCIPIOS GENERALES DEL MODELO.
Debido a limitaciones de espacio, la exposición que seguirá será necesariamente sintética. Para el lector interesado, la formulación original del modelo puede encontrarse en la monografía de Rasch (1960 Caps. II y VII). Una exposición matemáticamente más sofisticada puede hallarse en la obra de Lord y Novick (1968,Cap 21) dentro de la denominada «teoría fuerte de la puntuación verdadera». En castellano, puede encontrarse una clara introducción al modelo en Santisteban (1990, Cap. 8).
En forma general se plantea que la probabilidad de que un sujeto «j» obtenga «r» errores en un test «i» sigue una ley de Poisson expresable en la forma:
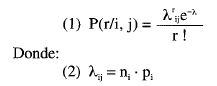
Es decir, el parámetro λ en la distribución se obtiene como el producto entre el número de items y la probabilidad de error en un ítem (que se considera constante en los ni ítems). Desde el enfoque adoptado para definir la distribución de Poisson, este parámetro sería la esperanza matemática de los errores. Desde un enfoque psicométrico clásico, (1) se puede considerar como la puntuación verdadera, es decir, como el número de errores esperados desde el modelo.
Desde estos supuestos comunes a todo proceso de Poisson, Rasch plantea que la probabilidad de error en un ítem se encuentra gobernada exclusivamente por dos parámetros: la dificultad del test (bi) y el nivel de habilidad del sujeto (xj). La relación entre ambos puede expresarse mediante:
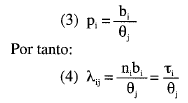
Donde τ recibe el nombre de «índice de impedimento» del test. La estimación de los parámetros correspondientes a los sujetos y a los ítems deberá hacerse desde los datos empíricos, es decir, desde la matriz de sujetos x tests, cuyos elementos son los errores observados.
Consideremos un sujeto «j» que responde a una serie de tests: 1, 2,...i...m, cometiendo en ellos e1, e2...... ei.. em errores. Suponiendo constante su nivel de habilidad xj es razonable plantear que:
![]()
Es decir, el total de errores observados en los tests será aproximadamente igual al total esperado desde el modelo. De ser así, el estimador de θj se deduce inmediatamente de (5).
Para estimar los parámetros correspondientes a los ítems, Rasch demuestra previamente la separabilidad de los parámetros correspondientes a sujetos y a ítems, así como la suficiencia del total de errores (Et) en la estimación de los niveles de habilidad.
En forma breve, el desarrollo es como sigue: asumiendo el cumplimiento de la ley de Poisson, se deduce que los errores totales cometidos en todos los tests dependerán de los niveles de habilidad de los sujetos ( θ); sin embargo, dado un determinado total, (Et), la distribución condicional de errores en los distintos tests (e1, ..ei..em) seguirá la ley binomial, independientemente de los niveles de habilidad. Es por esta razón que en (6) sólo se requiere el total de errores para estimar las θ.
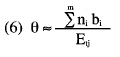
El estimador de los niveles de dificultad puede derivarse entonces separadamente del estimador de los niveles de habilidad y debe hacerse previamente puesto que se requiere para este último (ver 6). Por otra parte, de (3) se deduce claramente que la métrica en que se miden θ y b es arbitraria. Para solventar esta indeterminación, Rasch propone anclar uno de los tests en b=1 y estimar los restantes. La práctica habitual consiste en anclar el más difícil.
El estimador del índice de dificultad del test se obtendrá por:
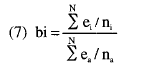
Donde «N» es el número de sujetos del grupo normativo y el subíndice «a» indica el test anclado.
Nótese que en la estimación de los parámetros b en (7) no intervienen los niveles de habilidad de los sujetos ( θ). Esto implica que, en caso de que el modelo sea adecuado, la dificultad estimada en el test será independiente de dichos niveles de habilidad. Asimismo, la habilidad estimada será la misma aunque los tests sean más fáciles o más difíciles. Es esta, como hemos dicho, la pretensión general del trabajo de Rasch y que hace tan atractiva la TRI: los parámetros de los tests son invariantes frente a grupos con niveles de habilidad distintos, mientas que las estimaciones de la habilidad son las mismas aunque la dificultad de los instrumentos varíe. Además, la dificultad y la habilidad se miden en una misma métrica.
Estimados los parámetros, podrán derivarse entonces los errores esperados para un sujeto en un determinado test, es decir, su puntuación verdadera, mediante (4). Asimismo podrá obtenerse la probabilidad esperada de que un sujeto obtenga un número determinado de errores en un test mediante (1). La contrastación entre valores observados y valores esperados indicará el ajuste del modelo a los datos empíricos. Rasch (1960) propone una prueba formal de significación basada en la distribución χ2: sin embargo defiende que puede ser más conveniente verificar el ajuste mediante representaciones gráficas que adherirse estrictamente a la prueba estadística. En este trabajo presentamos un procedimiento gráfico distinto al propuesto por Rasch que se describirá en el apartado de método.
EL TIEMPO DE INSPECCION: ESTIMACION Y PROBLEMAS
A partir de la década de los años 60 y, en conjunción con el desarrollo de las teorías del procesamiento de la información, hemos asistido a una utilización masiva de los indicadores relacionados con la llamada por Posner (1978) «cronometría mental». En esta línea cabe señalar el desarrollo de indicadores relacionados con estadios específicos del procesamiento humano de la información como el Tiempo de Inspección (TI en adelante). El TI como medida cronométrica se deriva de un modelo de discriminación perceptiva elaborado por D.Vickers (Vickers, 1970; Vickers, Nettelbeck y Wilson, 1972; Vickers y Smith, 1986), denominado «modelo acumulador». En dicho modelo se propone que el input estimular es muestreado con una tasa constante, almacenándose la evidencia en favor de cada alternativa en algún tipo de registro sensorial, hasta que la evidencia en favor de una u otra alternativa supera una constante crítica que provee a los mecanismos de selección y ejecución de respuesta de la información necesaria sobre la naturaleza del estímulo.
Con el fin de elaborar un indicador que permitiera la verificación de dicho modelo, D. Vickers y sus colaboradores se plantearon la presentación de un estímulo cuya discriminación fuera tan simple que permitiera el funcionamiento de los sistemas de decisión mediante una única inspección. Usualmente, dicho estímulo consiste en dos líneas verticales de distinta longitud unidas en su parte superior por una línea horizontal. Las líneas que componen el estímulo son cubiertas por una figura cuyo cometido es generar un proceso de enmascaramiento retroactivo de tal modo que el sujeto no pueda realizar un procesamiento posterior del estímulo a partir de la información existente en los registros sensoriales. A partir de todo ello, se define el TI como el tiempo de exposición mínimo que necesitan los sujetos para responder ante tal estímulo en un porcentaje elevado de las presentaciones que generalmente se situa alrededor del 95 % (Vickers et al, 1972; Nettelbeck, 1987).
Principalmente se han utilizado dos métodos básicos en la estimación del TI, derivados de los utilizados tradicionalmente en la psicofísica. El método de los estímulos constantes y los denominados métodos adaptativos. En el primer caso el porcentaje de aciertos del sujeto bajo una serie de tiempos de exposición prefijados se ajusta a un modelo de ojiva normal, con el fin de estimar el tiempo de exposición necesario para la tasa de aciertos requerida en la estimación del TI. En el segundo, tal y como indica su nombre, el tiempo de exposición de cada ensayo se determina en función del rendimiento del sujeto en los ensayos precedentes.
Ambos métodos presentan una serie de ventajas e inconvenientes. Así el método de los estímulos constantes permite unos criterios más severos en lo relativo al porcentaje de aciertos utilizados como criterio para establecer el TI. Los métodos adaptativos por su parte, utilizan unos criterios más laxos (alrededor del 85% de aciertos) aunque, por otra parte, precisan de una menor duración de la prueba y presentan un mayor número de ensayos en las inmediaciones del nivel crítico (Irwin, 1984). Por otra parte mediante ambos métodos se alcanza una fiabilidad test-retest relativamente elevada (entre r=0.70 y r=0.90) aunque inferior a la que presentan otras medidas cronométricas que suelen oscilar entre r=0.95 y r=0.98 (Nettelbeck 1987).
OBJETIVOS
En el presente trabajo se propone la utilización del modelo Poissoniano I de Rasch en el escalamiento simultáneo de las dificultades de algunas tareas de TI así como de los niveles de capacidad de los sujetos. Tal como han sido planteadas, las tareas se ajustan bien a las condiciones requeridas por el modelo; constan de un elevado número de ítems (ensayos) y resulta apropiado considerar que su dificultad es la misma en todos los ensayos, en otras palabras, parece claro que interesa más el número de errores que el ensayo particular en que se comete el error. Por otra parte, dado que el tiempo de exposición es constante, puede considerarse que el éxito o fracaso en un determinado ensayo es localmente independiente del éxito o fracaso en otro cualquiera.
En caso de que el modelo ajuste satisfactoriamente, podría disponerse de una serie de tareas calibradas según su índice de dificultad que permitirían obtener, en forma relativamente simple, estimaciones de los niveles de capacidad de los sujetos.
MÉTODO
Sujetos:
La tarea fue administrada a 40 sujetos voluntarios, estudiantes de primer ciclo de la Facultad de Psicología de la U.R.V. (24 varones y 16 mujeres) de edades comprendidas entre los 19 y 25 años.
Instrumentos:
Ordenador PC 386/33 con coprocesador matemático.
Programa para la presentación de estímulos «dinamic» (Vigil, Lorenzo y Ferrando, 1992). Programa para la calibración de tests según el modelo uno de Poisson «poisson» (Ferrando y Lorenzo, 1993).
PROCEDIMIENTO
Administración:
La tarea consistió en la presentación de una serie de 300 exposiciones al estímulo utilizado. En cada ensayo, el tiempo de exposición al estímulo se elegía aleatoriamente entre tres opciones: 90, 110 y 130 milisegundos. La figura utilizada fue la clásica propuesta por Vickers et al. (1972) que consistía de dos líneas verticales de 26 y 13 mm. de longitud con una separación entre las mismas de 18 mm y un grosor de 2 mm, unidas en su parte superior por una línea horizontal. Los estímulos fueron presentados mediante la pantalla del ordenador, controlada por una tarjeta SVGA de 1 Mb.
La presentación de los estímulos así como el registro de las respuestas fue controlada mediante un programa desarrollado en el interprete / compilador Quick Basic 4.0, respondiendo el sujeto mediante un ratón Genious Mouse GM6. La precisión del reloj interno (timer) del ordenador se controló tomando como unidad de medida la diezmilésima de segundo mediante una subrutina en lenguaje ensamblador (Bührer, Sparrer y Weitkunat, 1987; Graves y Bradley, 1987).
Con el fin de obtener una estimación del TI que no se vea afectada por la utilización de estrategias de respuesta basadas en el movimiento aparente, se ha utilizado el método desarrollado por Knibb (1992), basado en la utilización de una máscara dinámica. Dicha máscara consiste de 6 figuras que se superponen, formadas aleatoriamente por recuadros blancos y negros y grises. De este modo se consigue generar un movimiento aparente en direcciones aleatorias, que a diferencia del generado por los sistemas de enmascaramiento clásico, no aporta ninguna información sobre la figura utilizada para evaluar el TI.
Análisis:
Para la calibración de tareas y sujetos de acuerdo al modelo, se desarrolló un programa en Fortran 77 que llevaba a cabo las estimaciones de parámetros de según las expresiones (6) y (7).
Respecto a la verificación de ajuste del modelo, se desarrolló un método elemental que pasamos a describir:
Una vez determinados los parámetros θ y b, pueden obtenerse mediante (2) los errores esperados desde el modelo para cada uno de los sujetos en los distintos tests. Si, en cada test, se representan en un gráfico bivariado los errores esperados (en abcisas) y los observados (en ordenadas) para cada uno de los sujetos, entonces, en caso de un ajuste apropiado, la nube de puntos caerá muy próxima a una recta de regresión con pendiente 1. El coeficiente de correlación tenderá también a 1 y la varianza de error (1-r2) a cero. Cuanto más nos alejemos de estos valores, peor será el ajuste del modelo.
El programa antes citado, producía también los gráficos bivariados para cada test y calculaba la pendiente de regresión, el coeficiente de correlación y la varianza de error.
RESULTADOS
Tabla I: Estimadores de los niveles de dificultad en los tres tests.
Estimadores índices de dificultad
|
TEST
|
N.° 1
|
.13
|
|
TEST
|
N.° 1
|
.24
|
|
TEST
|
N.° 1
|
1.00
|
Como cabe apreciar, el nivel correspondiente a un tiempo de exposición de 80 milisegundos resulta notablemente más difícil que los otros dos. Si, como plantea Rasch (1960) suponemos a los estimadores medidos en escala de razón, entonces el tercer nivel resulta unas cuatro veces más difícil que el segundo, mientras que el segundo es sólo el doble de difícil que el primero. Cara a posibles futuras investigaciones, este resultado sugiere la necesidad de elegir un valor intermedio más difícil.
Aún con el reducido número de observaciones para un trabajo de este tipo, cabe observar, que los resultados indican un ajuste razonablemente bueno, especialmente respecto al test más difícil. La explicación se deduce ya de la inspección de la matriz de datos.
El test más difícil, como ya se ha comentado, lo es mucho más que los otros dos; esto significa que en dicho test, todos los sujetos cometen un número de errores claramente más elevado que en cualquiera de los otros dos.
Estos otros dos tests tienen niveles más similares lo que implica que en algunos casos no se mantenga el orden esperado desde el modelo; así, algunos sujetos, pueden cometer un error en el test más fácil y ninguno en el segundo, o bien cero errores en los dos primeros, etc.
DISCUSION
En principio resulta evidente que la muestra utilizada es muy reducida para un trabajo de este tipo. La calibración de cualquier test exige, en general, trabajar con grupos normativos más numerosos. Sin embargo, cabe decir al respecto que en este trabajo tan sólo se pretenden evaluar las posibilidades de aplicación del modelo a este tipo de tareas. La calibración de estas se plantea como objetivo en futuros trabajos.
A pesar de esta limitación, no parece descabellado concluir que el modelo se presta al análisis de tareas como las aquí utilizadas. Sin embargo, los resultados mostrados en el apartado anterior llevan a una serie de consideraciones.
En primer lugar parece obvio que el modelo se ajustará mejor cuanto más claramente difieran los tests en nivel de dificultad. La elección «a priori» de niveles apropiados se muestra, por tanto, como un aspecto de notable importancia.
Si se pretenden calibrar tareas con niveles de dificultad más similares, entonces deberá aumentarse de alguna forma la sensibilidad del análisis. A este respecto, conviene recordar que el modelo se aplica a tareas de larga duración y con muy baja probabilidad de error. Si se espera que las diferencias emerjan con mayor claridad, debe aumentarse el tamaño del grupo normativo o bién, aumentar la longitud de las tareas, o bién ambos. Desde los supuestos básicos del modelo, la mejor solución sería aumentar la longitud de la tarea ya que, como es sabido, el modelo se plantea como un límite cuando n tiende a infinito. En consecuencia, asumiendo que sea apropiado, las esperanzas de error se acercarán más a los valores observados cuantos más elementos tenga la tarea.
Desde el punto de vista aplicado, cabe decir sin embargo que los voluntarios de esta experiencia consideraron que la tarea se les hacía pesada con su longitud actual. Si se pretende proponer al modelo como alternativa de calibración debe tenerse en cuenta que si su administración resulta costosa, entonces probablemente no resulte viable frente a métodos más breves y de similar eficacia.
En suma, como es habitual en este tipo de trabajos, se hace evidente la necesidad de llevar a cabo más estudios sobre el tema.
REFERENCIAS
Bührer, M; Sparrer, B; y Weitkunat, R. (1987) Interval Timing Routines for the IBM PC/XT/AT Microcomputer Family. Behavior Research Methods Instruments and Computers. 19(3): 327-334.
Ferrando, P. J. y Lorenzo, U.(1993) Desarrollo de un Programa en Fortran para la Estimación de los Parámetros en el Modelo Poissoniano de Rasch. Universitas Tarraconensis. 15: 87-98.
Graves, R; y Bradley, R. (1987) Millisecond interval timer and auditory reaction time programs for the IBM PC. Behavior Research Methods, Instruments and Computers. 19 (1): 30-35.
Goodstein, H y Wood, R. (1989) Five Decades of Item Response Modelling. British Journal of Mathematical and Statistical Psychology. 42: 139-167.
Haight, F. A. (1967) Handbook of the Poisson distribution. New York. Wiley.
Irwin. R. J. (1984) Inspection Time and its Relation to Intelligence. Intelligence. 8:47-65.
Knibb, K. (1992) A Dynamic Mask for Inspection Time. Personality and Individual Differences. 13: 237-248.
Lord, F. M. y Novick, M. R. (1968) Statistical theories of mental tests scores. Massachusetts. Addison-Wesley
Nettelbeck, T. (1987) Intelligence and Inspection Time. En P. A.Vemon (Ed.) Intelligence and Speed of Information Processing. New York. Ablex.
Posner, M. I. (1978) Chronometric Explorations of Mind. Erlbaum. Hillsdale.
Rasch, G. (1960) Probabilistic models for some intelligence and attainment tests. Copenhagen. Danmarks Paedag. Institut.
Santisteban, P. (1990) Psicometría: Teoría y Práctica en la Construcción de Tests. Madrid. Norma.
Vickers, D. (1970) Evidence for an Accumulator Model of Psychophysical Discrimination. Ergonomics. 13: 263-269.
Vickers, D; Nettelbeck, T; & Wilson, R. J (1972) Perceptual Indices of Performance: The Measurement of I. T. and Noise in Visual Stimulation. Perception. 1: 263-295.
Vickers. D. y Smith, P. L. (1986). The Rationale for Inspection Time Index. Personality and Individual Differences. 7: 609-623.
Vigil, A; Lorenzo, U; y Ferrando, P. J. (1992). Desarrollo de un Programa de Enmascaramiento Dinámico para la Estimación del Tiempo de Inspección. Psicológica. 13: 345-355.
Aceptado el 10 de mayo de 1993