Psicothema was founded in Asturias (northern Spain) in 1989, and is published jointly by the Psychology Faculty of the University of Oviedo and the Psychological Association of the Principality of Asturias (Colegio Oficial de Psicología del Principado de Asturias).
We currently publish four issues per year, which accounts for some 100 articles annually. We admit work from both the basic and applied research fields, and from all areas of Psychology, all manuscripts being anonymously reviewed prior to publication.
Psicothema, 2003. Vol. Vol. 15 (nº 2). 315-321
Ana Hernández and Vicente González-Romá
Universidad de Valencia
We use simulated data to evaluate the adequacy of the Multiple-Group (MG) extension of the Confirmatory Factor Analysis (CFA) with Mean and Covariance Structure (MACS) model for the detection of differential item functioning (DIF) in polytomous graded response items. Two factors are varied to generate the DIF conditions: type of DIF (uniform and non-uniform) and size of DIF (low, medium and high). For each condition, 100 samples (N= 800) are generated according to the Graded Response model. Ten items with 5-response categories are considered, and only one item is manipulated to show DIF. The data are analyzed by means of LISREL 8. Results show that the DIF detection procedure analyzed reasonably maintained control of its Type I error under non-uniform DIF conditions, but showed some difficulties under uniform-DIF conditions. With respect to power, the procedure was satisfactory for detecting medium and high uniform DIF, and lacked power for detecting non-uniform DIF.
Evaluación del modelo multigrupo de análisis de estructuras de medias y covarianzas para la detección del funcionamiento diferencial de ítems politómicos de respuesta graduada. Se evalúa la adecuación de la extensión multigrupo del análisis factorial confirmatorio con estructura de medias y covarianzas latentes (MG-CFA-MACS) para el análisis del funcionamiento diferencial de los items (DIF) con escala de respuesta ordinal. Se manipulan dos factores para simular las condiciones de DIF: el tipo de DIF (uniforme y no uniforme) y la magnitud del DIF (bajo, medio y alto). A partir del modelo de respuesta graduada se generan 100 muestras (N= 800) de 10 items con 5 alternativas de respuesta. Sólo un ítem es manipulado para generar DIF. Los resultados obtenidos mediante LISREL 8 muestran que el procedimiento analizado controló la tasa de error tipo I bajo condiciones de DIF no-uniforme, pero tuvo ciertas dificultades en condiciones de DIF uniforme. En relación con la potencia, el procedimiento resultó satisfactorio en las condiciones de DIF uniforme medio y alto, pero manifestó una potencia inadecuada para detectar el DIF no-uniforme.
Differential Item Functioning (DIF) constitutes a potential threat to the validity of a test. Both the APA (American Psychological Association) and the ITC (International Test Commission) standards emphasize the necessity of checking for DIF in order to guarantee the fair use of a test (AERA, APA, NCME, 1999; COP-ITCx, 2000). With these recommendations in mind, and with the intention of spreading the application of DIF analyses, researchers should develop and assess DIF detection methods that would be easily implemented by practitioners lacking a highly technical or statistical background.
Focusing on polytomous graded response items, a number of methods have been proposed to detect both uniform and non-uniform DIF (see Potenza & Dorans, 1995; Hidalgo & Gómez, 1999). One of these methods is based on a popular technique among psychologists: Factor Analysis. In this paper, we evaluate a Factor-Analysis-based DIF detection method: the Multiple Group Confirmatory Factor Analysis with Mean and Covariance Structure (MG-CFA-MACS).
In the last few years, the MG-CFA-MACS has attracted the attention of DIF researchers and has been frequently applied for the evaluation of both uniform and non-uniform DIF on polytomous items with ordered response alternatives (Everson, Millsap & Rodriguez, 1991; Byrne, 1998; Tomás, González-Romá, & Benito, 2000; Chan, 2000; Wasti, Bergman, Glomb, & Drasgow, 2000). Taking into account that all these studies have used empirical data, the extent to which using a continuous response model such as the MG-CFA-MACS is adequate for the correct detection of DIF on polytomous ordered response items must be clarified. The present study addresses this issue using simulated data.
Analyzing polytomous graded response items by means of the Confirmatory Factor Analysis with Mean and Covariance Structure model
When using items with ordered response categories such as Likert-type rating scales, it is assumed that a latent unidimensional continuous variable (ξ) underlies the item responses. In responding to these kinds of items, the subjects locate themselves on the latent continuum by selecting the response category that best expresses their position on that continuum. Successive integers are assigned to the successive m categories in such a way that they cumulatively reflect the measured construct.
Using polytomous graded response items, it can be assumed that the item responses are approximations of continuous responses (Ferrando, 1996; Mellenbergh, 1994). Based on this assumption, the Confirmatory Factor Analysis (CFA) with Mean and Covariance Structure (MACS) model (Sörbom, 1974), which is a method for analyzing continuous items, can be applied to the analysis of polytomous ordered response items. In this model, the item response of the individual i to the item j, Xij can be explained by means of the linear regression of Xij on the latent trait variable ξi as:
Xij= µj + λjξj + δij (1)
The regression intercept, µj, represents the expected mean response to item j for subjects at the latent trait value of zero. The regression coefficient or factor loading, λj , refers to the expected change in the item response Xij per unit change in ξi. Finally, δij is the random error term. Within the CFA-MACS model, the item intercept corresponds to the item location or attractiveness parameter, whereas the item factor loading corresponds to the item discrimination parameter (Ferrando, 1996; Mellenbergh, 1994).
Evaluation of DIF by means of the MG-CFA-MACS model
An item shows DIF when individuals with equal levels on the latent trait respond differently to the item depending on group membership. DIF can either be uniform or non-uniform depending on which item parameter, location or discrimination, is not invariant across the groups of interest. The location or attractiveness parameter corresponds to the expected mean item response value for a given trait level. The item discrimination parameter refers to the ability of the item to differentiate among people with different latent trait levels. The higher the discrimination parameter, the better the item distinguishes among people with similar levels on the latent trait.
The Multiple-Group (MG) extension of the CFA-MACS model allows researchers to test both uniform and non-uniform DIF according to group membership. The MG-CFA-MACS is formulated as:
![]()
where µj, ,λj, and δij are defined as in equation 1 and g refers to group membership.
In general terms, testing the null hypothesis that parameter µj is invariant across groups [e.g., µ j(1) = µ j(2) = … = µ j(G) ] allows researchers to test the presence of uniform DIF, whereas testing the null hypothesis that parameter λj is invariant across groups [e.g., λj(1) = λj(2) = …= λj(G) ] allows researchers to test the presence of non-uniform DIF.
The iterative DIF detection procedure, based on the MG-CFA-MACS model analyzed here, uses modification indices (MI) for detecting which specific items function differentially across groups (Chan, 2000). A MI shows the reduction in the model’s chi-square value if the implied constrained parameter is freely estimated. Because this chi-square difference is distributed with one degree of freedom, it is easy to determine whether the reduction in chi-square is statistically significant. The procedure starts with a fully equivalent model in which all the item factor loadings and the intercepts are constrained to be equal across groups. Then the non-uniform DIF is evaluated. Specifically, the largest modification index (MI) associated with the factor loading estimates is evaluated to determine its statistical significance. If the largest lambda MI is statistically significant, the conclusion can be drawn that the corresponding item exhibits non-uniform DIF across the two groups. Then, a new model is fitted. In this model, the factor loading that showed a statistically significant MI is freely estimated, while the remaining lambda estimates are constrained to be equal in both groups. The largest MI associated with the lambda estimates is evaluated again to determine its statistical significance, and this iterative procedure continues until the largest MI is not statistically significant. After evaluating non-uniform DIF, the procedure focuses on uniform DIF to determine the statistical significance of the MIs associated with the intercepts. If the largest MI associated with the intercepts is statistically significant, it can be concluded that the corresponding item exhibits uniform DIF across groups. As before, a new model is fitted in which the corresponding intercept is freely estimated, while the remaining intercepts are constrained to be equal in both groups. The largest intercept MI is evaluated again to determine its statistical significance. This iterative procedure continues until the largest intercept MI is not statistically significant. Taking into account that each MI is evaluated multiple times, the Bonferroni correction should be used to test the significance of the reduction on chi-square at a specified alpha.
There is a simulation study that evaluates a different DIF detection procedure based on factor analysis: Oort’s (1992) restricted factor analysis method of item bias detection. Within this method, the common factor model serves as an item response model, and a different factor is included for each of the potential causes of DIF. However, this model does not make it possible to differentiate between uniform and non-uniform DIF. Oort (1998) carried out a simulation study to test the adequacy of the model he proposed for the detection of DIF on polytomous graded response items. The results of this study showed that the model was adequate for the evaluation of DIF in items with seven response categories, especially when the sample size was large, the mean trait difference between the focal and reference groups was small, the sizes of both groups were equal and the amount of bias was large. But, even when the number of response categories was reduced to two, this continuous approximation was as good as an established method based on the one-parameter logistic item response model. Moreover, results also showed that when the number of categories was seven, it was better to use an iterative procedure for the detection of DIF than a non-iterative procedure.
In summary, the MG-CFA-MACS continuous approach has been used for the evaluation of DIF in polytomous items with an ordered response format (e.g., Chan, 2000). However, the adequacy of this approximation for the detection of DIF has never been tested. Consequently, the main aim of the present paper is to study the extent to which the MG-CFA-MACS model is adequate for the detection of DIF in non-continuous items, specifically in polytomous items with an ordered response format. To attain this objective, the Graded Response Model (GRM) proposed by Samejima (1969) for the analysis of polytomous items is employed to simulate the data of the focal and reference group. Then the MG-CFA-MACS model is fitted to evaluate DIF.
To date, the adequacy of this continuous approach for the detection of DIF has not been evaluated in simulated data. Although Oort (1998) carried out a Monte-Carlo study to evaluate a continuous approximation of the CFA in the detection of DIF, he did it from a different model that does not allow researchers to test uniform and non-uniform DIF and that, in fact, has not been applied as often as the MG-CFA-MACS model in empirical research. Consequently, the MG-CFA-MACS model is the focus of attention in the present study.
Method
Simulation of data
The simulation process started with the generation of both the reference and focal trait levels according to a standard normal distribution N(0,1). The item responses were generated according to the Graded Response Model (Samejima, 1969), probably one of the most widely used IRT models to analyze polytomous graded response items. In this model, the probability of person i responding above category k to item j, that is, the boundary response function (BRF), is:
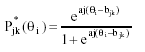
where aj is the discrimination parameter for item j; bjk is the kth boundary parameter for the jth item, which corresponds to the level of trait at which P* jk (θs) is .50; and θi is the trait level parameter for person i. For an item with m response categories, there are mj-1 BRFs determined by a discrimination parameter aj and mj-1 location parameters bjk.
In order to simulate realistic conditions in the field of personality and attitude measurement, the sample sizes of the reference and the focal group were set at 800, and 10 items with five response options were considered. Ten items is a usual number for the measurement of personality and attitudes (for instance, see the Fifth Edition of the 16PF Questionnaire). Five categories is also a frequent number in this context, and it is the minimum recommended by different authors (Bollen & Barb, 1981; Dolan, 1994) to adequately represent the subject’s scores on graded response items by means of the CFA-MACS model. To select the parameter values, a 22-item Job Satisfaction questionnaire was employed. The unidimensionality of this questionnaire had been previously tested in a sample made up of 932 subjects (González-Romá, Peiró & Tordera, 2002). The results were satisfactory, with the exception of one item that showed a low loading (λ = .24) and, therefore, was excluded in the subsequent analyses. To select the item parameters to be used in the data simulation, the Graded Response Model (GRM) (Samejima, 1969) was fitted. Two requirements had to be met for the selection of the item parameters: 1) Taking into account that some studies have shown that differential item skewness has important effects on the adequacy of the CFA-MACS when applied to polytomous graded response items (Ferrando, 1999; Olsson, 1979), only items showing a skewness with an absolute value under 1 were selected; and 2) After adjusting the GRM to the non-skewed selected items, only items with bjk estimates of between –2.5 and 2.5 were selected, in order to guarantee that all the response options were represented in the data and that the estimates were accurate enough.
Apart from a non-DIF condition in which all the 10 item parameters were equal for both groups, two factors were varied in order to create different DIF-conditions: the type of DIF (uniform and non-uniform) and the magnitude of DIF (low, medium and high). In these conditions the bk parameters or the a parameter of one item (item 10) were varied across groups (for the uniform and non-uniform DIF conditions, respectively). For the uniform DIF conditions, the four bk parameters of item 10 for the focal group were obtained by adding a constant to the four bk parameters of the reference group. Consequently, item 10 was less attractive for the focal group. For the non-uniform DIF conditions, the a parameter of item 10 for the focal group was obtained by subtracting a constant from the reference group discrimination parameter. Consequently, item 10 was less discriminative for the focal group. To make both uniform and non-uniform DIF comparable, the constant values were selected to obtain the same differences between the areas of the expected item response functions for both the reference and the focal groups.
The expected item response function is ![]() ,
,
where ukj is the weight for response category k of item j and Pjk(θi) is the probability that examinee i will choose category k for item j. The unsigned area measure (UA, see Cohen, Kim, & Baker, 1993), to estimate the area between the item response functions of each group, can then be obtained from the equation
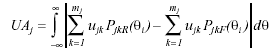
Three sizes of differences between the areas were considered: .50, 1 and 1.50 for the low, medium and high DIF conditions, respectively. Approximating the unsigned area for 70 intervals between θ = -3.5 and θ = 3.5, we found that, for the low DIF condition, the required group difference in the a parameters to reach an area difference of .50 was .33, whereas the required difference in each of the four b parameters to reach an area difference of .50 was .125. The required differences in the a and b item parameters to reach an area difference of 1 were .55 and .25, respectively. The corresponding differences in the a and b item parameters to produce an area difference of 1.5 were .73 and .375, respectively. The item 10 parameters for the different DIF conditions are displayed in Table 1.
Thus, seven conditions were evaluated (2 types of DIF x 3 magnitudes of DIF + 1 non-DIF condition). For each condition, 100 samples were generated.
After having the item parameters and the simulated subjects’ trait levels, P*jk (θi) was calculated for every examinee. Then, for each simulated subject i a single random number (Y) was sampled from a uniform distribution over the interval [0,1], and the item scores were assigned as follows: If Y was smaller than the probability of responding above category k and greater than the probability of responding above category k+1, then the score assigned was k. For the 5-category items simulated:
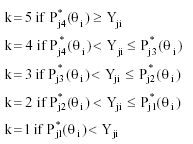
It should pointed out than when uniform DIF was generated by means of the GRM, only the bk parameters were varied across groups. Consequently, only differences in the intercepts estimated by means of the MG-CFA-MACS were expected, because the thresholds between adjacent categories, but not the item slopes, are different. However, when non-uniform DIF was generated in our data, although only the a parameter was changed across groups, differences in both the intercepts and the slopes, estimated by means of the MG-CFA-MACS, were expected. The reason is that when the slope is changed, the distance between the thresholds of adjacent categories changes too, regardless of whether the response boundary parameters bk are equal or not. Consequently, the expected item score at a specific level of the latent trait will change too, and this variation will be reflected in the intercept, which is the expected item score at the trait level of 0, that is μj = E(Xj ¦ θ = 0). The more different the slopes between groups are, the more different the intercepts are expected to be. For example, for the low non-uniform DIF condition, the expected difference between intercepts was .01 (µReference - µ Focal = .01), whereas for the medium and high non-uniform DIF conditions, the expected differences were µR- µ F = .10 and µR - µF = .16 , respectively.
Analysis
Analyses were carried out by means of LISREL 8 (Jöreskog & Sörbom, 1993), using Maximum Likelihood (ML) estimation. Because skewness and kurtosis of variables from which data were generated were minimal (skewness ranged from –.92 to .37, and kurtosis ranged from -.72 to -.007), the assumption of approximate normality and the use of ML estimation techniques can be supported (Bollen, 1989). The Multiple-Group CFA-MACS model was fitted to the 10 x 10 item variance-covariance matrices and vectors of 10 means of both the reference and the focal groups. To detect uniform and non-uniform DIF, a series of nested multiple-group single factor models were tested according to the iterative procedure described in the introduction (Chan, 2000). At each step of this iterative procedure a maximum of 10 MIs was considered. Therefore, in order to determine the statistical significance of each MI, the alpha value was set at .05/10 = .005, applying the Bonferroni correction.
For all the models, a number of constraints was imposed for model identification and scale purposes. First, an item was chosen as the reference indicator (specifically item 4). This item factor loading was set to 1 in both groups, in order to scale the latent variable and provide a common scale in both groups. Second, the factor mean was fixed to zero in the reference group for identification purposes, whereas the factor mean in the focal group was freely estimated. Finally, the reference indicator intercepts were constrained to be equal in both groups, in order to identify and estimate the factor mean in the focal group and the intercepts in both groups (Sörbom, 1982).
Results
Two indicators were calculated to determine the accuracy of DIF detection: 1. the true positive (TP) ratio or proportion of correct identifications of item 10 for the DIF conditions, and 2. the false positive (FP) ratio or proportion of incorrect DIF identifications of items 1 to 9 for the 6 DIF conditions, and of items 1 to 10 for the non-DIF condition. An item was considered to show DIF when the decrement in chi-square shown by the corresponding MI was statistically significant (that is, equal to or greater than χ2(.005,1)= 7.88). The results are separately considered in the following paragraphs according to the different DIF conditions.
Focusing on the non-DIF condition, the results obtained showed that both the proportion of FPs in the intercept, that is, the proportion of items that were detected as showing uniform DIF, and the proportion of FPs in the factor loading, that is, the proportion of items that were detected as showing non-uniform DIF, were .008. According to Bradley (1978), an observed proportion of false positives is robust at a nominal significance level of .005 if it is between 0.0025 and .0075. Thus, although the observed ratio of .008 is very close to the assumed nominal level of .005, rigorously speaking, it is not robust. We also computed the proportion of items incorrectly flagged as DIF items, regardless of whether they were flagged by statistically significant MIs associated with item intercepts or by statistically significant MIs associated with item factor loadings. This proportion was computed as follows: (proportion of items wrongly flagged as DIF items because of statistical significance of their intercepts’ MIs) + (proportion of items wrongly flagged as DIF items because of statistical significance of their factor loadings’ MIs) – (proportion of items wrongly flagged as DIF items because of statistical significance of their factor loadings’ MIs and their intercepts’ MIs). For the non-DIF condition this proportion equaled 0.016.
With regard to the DIF conditions, the proportion of FPs and the proportion of TPs (in both l, and m parameters) are shown in Table 2 for both uniform and non-uniform DIF conditions and for the three considered DIF sizes. Column c contains the constant values that were added to the reference group bk parameters or subtracted from the reference group a parameter to obtain the focal group parameters.
Starting with the uniform DIF conditions, we recall that only the identification of DIF in the intercept of item 10 was considered a correct identification. Results showed a different pattern for the proportion of FPs depending on the parameter evaluated. For the three DIF sizes (low, medium, and high), the proportion of FPs in which DIF was wrongly detected in μ (.002, .001, and .005, respectively) was equal to or less than the nominal alpha value of .005. However, the proportions of FPs in which DIF was wrongly detected in λ (.011, .009, .013 ) were higher than the nominal value of .005, and they were not robust according to Bradley’s (1978) criterion. The proportions of items incorrectly flagged as DIF items, regardless of whether they were flagged by statistically significant MIs associated with item intercepts or by statistically significant MIs associated with item factor loadings, were .013, .010, and .018, for the low, medium, and high DIF sizes, respectively. As we expected, the proportion of TPs in which DIF was correctly detected in µ increased as the DIF size increased. Specifically, the proportion of TPs in the Low DIF condition was equal to .16, whereas the proportion of TPs in the Medium DIF condition was equal to .88. DIF was perfectly detected in the High DIF condition.
Finally, with regard to the non-uniform DIF conditions, DIF identifications in both item 10 discrimination and location parameters were considered correct identifications. In this case, results showed that, for all DIF sizes, the proportion of FPs was less than the nominal level of .005 in four out of the six cases. In the two cases in which this proportion exceeded .005, the observed values were less than .0075. The proportions of items incorrectly flagged as DIF items, regardless of whether they were flagged by statistically significant MIs associated with item intercepts or by statistically significant MIs associated with item factor loadings, were .008, .006, and .010, for the low, medium, and high DIF sizes, respectively. The proportion of TPs in which DIF was correctly detected in λ and in μ increased as the DIF size increased. However, compared with the uniform-DIF conditions, greater differences were necessary in the item parameters across groups to attain TP ratios far from zero. The proportions of TP were .01 and 0, for λ and μ , respectively, in the low DIF condition. They increased to .06 and .03, respectively, in the medium DIF condition, and to .44 and .19 in the high DIF condition. For the non-uniform DIF conditions, we computed the proportion of items correctly flagged as DIF items, regardless of whether they were flagged by statistically significant MIs associated with item intercepts or by statistically significant MIs associated with item factor loadings. These proportions were .01, .09 and .56 for the low, medium and high DIF conditions, respectively.
Discussion
This study evaluated the adequacy of a procedure based on the Multiple-Group Confirmatory Factor Analysis with Mean and Covariance Structure (MG-CFA-MACS) for the detection of DIF on polytomous graded response items. The adequacy of the model was evaluated according to the proportion of correct identifications of the DIF item (True Positive (TP) ratio or power) and the proportion of incorrect identifications of non-DIF items (False Positive (FP) ratio or Type I error) on both the location and discrimination parameters.
Results showed that the proportion of FPs stayed close to the nominal alpha level for the non-DIF condition and for all the non-uniform DIF conditions. However, for the uniform-DIF conditions the results obtained showed a different pattern for the proportion of FPs depending on the parameter evaluated. For the three DIF sizes considered, the proportion of FPs in which DIF was wrongly detected in μ was equal to or less than the nominal alpha value, whereas the proportion of FPs in which DIF was wrongly detected in λ was higher than the nominal alpha value of .005. If we focus on the proportion of items incorrectly flagged as DIF items, regardless of whether they were flagged by statistically significant MIs associated with item intercepts or by statistically significant MIs associated with item factor loadings, a different pattern of results appears depending on the type of DIF: this proportion was lower for the non-uniform DIF conditions than for the uniform-DIF conditions. Overall, these results point out that the DIF detection procedure analyzed maintained reasonable control of its Type I error under non-uniform DIF conditions, whereas under uniform-DIF conditions the procedure analyzed showed slight difficulties in maintaining control of its Type I error.
Regarding the TP proportion, the results obtained depended on the type and magnitude of DIF. Focusing on the uniform-DIF conditions, where only the location parameters were expected to vary, results showed that in the Low DIF condition, in which the difference between the bk parameters of the reference and the focal groups was set to .125, the proportion of TPs was only .16. However, for the medium and High DIF conditions, differences of .25 and .375 between the bk parameters resulted in 88% and 100% of correct identifications, respectively. For the uniform-DIF conditions, the expected differences in E(X) between the reference and the focal group when the latent trait value was 0, that is, the expected differences between the intercepts, were .07, .19 and .309 for the low, medium and high DIF conditions, respectively. Therefore, it is possible to conclude that differences in the intercept of about 0.19 are needed to achieve satisfactory rates of correct DIF identifications (about 88%) in the intercept. The implications of this result for the detection of uniform DIF using the MG-CFA-MACS are remarkable. If we take into account that the items simulated in this study showed a response scale ranging from 1 to 5, we can conclude that the MG-CFA-MACS is very sensitive to small differences across groups in the item intercept. Overall, the results obtained point out that, under uniform-DIF conditions, the power of the procedure analyzed was affected by DIF size (as we expected), and that the DIF detection procedure showed a satisfactory power to detect DIF when its size was medium and high.
Focusing on the non-uniform DIF conditions, where both item parameters (the intercept and the factor loading) were expected to vary, results showed that the procedure analyzed here lacked the power to consistently detect DIF. The maximum power (.44) was achieved when DIF size was high and the factor loading was the involved parameter. Comparing the power results obtained for the uniform and the non-uniform DIF conditions, the conclusion can be drawn that the DIF detection procedure analyzed shows differential sensitivity to both types of DIF.
This study shows a number of limitations that should be overcome in future research. First, the use of the GRM has the disadvantage that, given a specific magnitude of DIF according to this area measure, changes in the slope parameters are expected to produce changes in both the discrimination parameter (the item factor loading) and the location parameter (the intercept). So, only one type of non-uniform DIF (mixed) can be generated and evaluated. New studies must be developed using models such as the Generalized Partial Credit Model (GPCM) (Muraki, 1992), which will allow researchers to generate and evaluate symmetric non-uniform DIF. Second, this study has focused on favorable circumstances for the CFA-MACS model to adequately represent the polytomous graded response items: the number of categories is five (the minimum required for this continuous approach to be applied (Bollen & Barb, 1981; Dolan, 1994)), and all the item responses show similar skews. Thus, different conditions, in which the number of categories or the item skews are varied, must be considered in future studies. Third, in the present simulation study only two factors were manipulated in order to create different DIF-conditions: the type of DIF (uniform and non-uniform) and the magnitude of DIF. The two groups of subjects that we simulated had identical latent trait distributions and the same size. Future studies should investigate the performance of the analyzed procedure when the comparison groups differ in latent trait distribution and in size. In the same way, factors such as the percentage of DIF items or Type I error should be varied too. Finally, when using the MG-CFA-MACS model, the reference or ‘anchoring’ indicator is assumed to be free of DIF. The consequences of using a DIF item as a reference indicator when this model is employed must be evaluated too.
Acknowledgements
The authors wish to thank the editor and anonymous reviewers for their helpful comments and suggestions.
American Educational Research Association, American Psychological Association and National Council on Measurement in Education (1999). Standards for educational and psychological testing. Washington DC: American Educational Research Association.
Bollen, K.A. (1989). Structural Equations with Latent Variables. New York: Wiley.
Bollen, K.A. and Barb, K.H. (1981). Person’s r and coarsely categorized measures American Sociological Review, 46, 232-239.
Bradley, J.V. (1978). Robustness? British Journal of Mathematical and Statistical Psychology, 31, 144-152.
Byrne, B.M. (1998). Structural equation modelling with Lisrel, Prelis and Simplis. Basic concepts, applications and programming. New Jersey: Lawrence Erlbaum Associates.
Chan, D. (2000). Detection of Differential Item Functioning on the Kirton Adaptation-Innovation Inventory using multiple-group mean and covariance structure analyses. Multivariate Behavioral Research, 35, 169-199.
Cohen, A.S., Kim, S. and Baker, F.B. (1993). Detection of Differential Item Functioning in the Graded Response Model. Applied Psychological Measurement, 17, 335-350.
Colegio Oficial de Psicólogos (COP) and Comisión Internacional de Tests (ITC) (2000). Directrices internacionales para el uso de los tests. Madrid: (International Guidelines for test use). Madrid: COP.
Dolan, C.V. (1994). Factor analysis of variables with 2, 3, 5 and 7 response categories: A comparison of categorical variable estimators using simulated data. British Journal of Mathematical and Statistical Psychology, 47, 309-326.
Everson, H.T., Millsap, R.E. and Rodríguez, C.M. (1991). Isolating gender differences in test anxiety: A Confirmatory factor analysis of the test anxiety inventory. Educational and Psychological Measurement, 51, 243-251.
Ferrando, P.J. (1996). Calibration of invariant item parameters in a continuous item response model using the extended Lisrel measurement submodel. Multivariate Behavioral Research, 31, 419-439.
Ferrando, P.J. (1999). Likert scaling using continuous, censored, and graded response models: effects on criterion-related validity. Applied Psychological Measurement, 23, 161-175.
González-Romá, V., Peiró, J.M. and Tordera, N. (2002). An examination of the antecedents and moderator influences of climate strength. Journal of Applied Psychology, 87, 465-473.
Hidalgo, M.D. and Gómez, J. (1999). Técnicas de detección de funcionamiento diferencial en ítems politómicos. Metodología de las Ciencias del Comportamiento, 1, 39-60.
Jöreskog, K. and Sörbom, D. (1993). LISREL 8. Structural equation modeling with the SIMPLIS command language. Hillsdale.
Mellenbergh, G.J. (1994). A unidimensional latent trait model for continuous item responses. Multivariate Behavioral Research, 29, 223-236.
Muraki, E. (1992). A generalized partial credit model: Application of an EM algorithm. Applied Psychological Measurement, 16, 159-176.
Olsson, U. (1979). On the robustness of factor analysis against crude classifications of the observations. Multivariate Behavioral Research, 14, 485-500.
Oort, F.J. (1992). Using restricted factor analysis to detect item bias. Methodika, 6, 150-166.
Oort, F.J. (1998). Simulation study of item bias detection with restricted factor analysis. Structural Equation Modeling, 5, 107-124.
Potenza, M.T. and Dorans, N.J. (1995). DIF assessment for polytomously scored items: A framework for classification and evaluation. Applied Psychological Measurement, 19, 23-37.
Samejima, F. (1969). Estimation of latent ability using a response pattern of graded scores. Psychometrika Monographs, 34 (Suppl. 17).
Sörbom, D. (1974). A general method for studying differences in factor means and factor structures between groups. British Journal of Mathematical and Statistical Psychology, 27, 229-239.
Sörbom, D. (1982). Structural equation models with structured means. In K.G. Jöreskog and H. Wold (Eds.), Systems under indirect observation (pp. 183-195). Amsterdam: North Holland.
Takane, Y. and de Leeuw, J. (1987). On the relationship between Item Response Theory and factor analysis of discretized variables. Psychometrika, 52, 393-408.
Tomás, I., González-Romá, V. and Gómez, J. (2000). Teoría de respuesta al ítem y análisis factorial confirmatorio: dos métodos para analizar la equivalencia psicométrica en la traducción de cuestionarios. Psicothema, 12, 540-544.
Wasti, S.A., Bergman, M.E., Glomb, T. M. and Drasgow, F. (2000). Test of the cross-cultural generalizability of a model of sexual harassment. Journal of Applied Psychology, 85, 766-778.