La revista Psicothema fue fundada en Asturias en 1989 y está editada conjuntamente por la Facultad y el Departamento de Psicología de la Universidad de Oviedo y el Colegio Oficial de Psicología del Principado de Asturias. Publica cuatro números al año.
Se admiten trabajos tanto de investigación básica como aplicada, pertenecientes a cualquier ámbito de la Psicología, que previamente a su publicación son evaluados anónimamente por revisores externos.
Psicothema, 2004. Vol. Vol. 16 (nº 3). 498-508
Guillermo Vallejo, P. Fernández, F. J. Herrero and N. M. Conejo
Universidad de Oviedo
In this article we examined the performance of a mixed model Kenward-Roger’s adjusted F-test based on the correct covariance structure and the multivariate extension of the modified Brown-Forsythe method in a mixed repeated measures design. These two procedures were compared with regard to their power and robustness when multisample sphericity and multivariate normality assumptions are violated separately and jointly. Monte Carlo comparison shows that, overall, both methods do a reasonable job of controlling the rates of error for both normal data, as well as certain types of non-normal data. With respect to power, the results indicate that the mixed model analyses using the true structure model was generally more powerful than the modified Brown-Forsythe procedure.
Procedimientos para contrastar efectos fijos en diseños de medidas repetidas cuando se incumplen los supuestos. En este artículo se examina el comportamiento de un modelo mixto con los grados de libertad ajustados mediante la corrección de Kenward-Roger y el procedimiento multivariado de Brown-Forsythe modificado en un diseño de medidas parcialmente repetidas. Estos dos enfoques fueron comparados con respecto a su potencia y robustez cuando los datos incumplían separada y conjuntamente los supuestos de normalidad conjunta multivariada y esfericidad multimuestral. Globalmente, las comparaciones Monte Carlo ponen de relieve que los dos enfoques controlaban adecuadamente las tasas de error cuando los datos eran normales, así como para cierto tipo de datos no normales. Sin embargo, el enfoque del modelo mixto basado en la verdadera estructura de covarianza tenía mayor sensibilidad para captar los efectos no nulos que el procedimiento de Brown-Forsythe modificado.
The repeated measures designs containing both between-subjects grouping variables and within-subjects variables, are used routinely in many disciplines, such as medicine, psychology and education. Although the nature of these designs is typically multivariate, when the assumptions of multivariate normality, homogeneity of the covariance matrices, and sphericity are satisfied, such designs can be analyzed by Scheffé’s (1956) univariate mixed model because its F tests are valid and uniformly most powerful for detecting treatment effects when they are present. When the sphericity assumption is not satisfied, either an adjusted degrees of freedom (df) univariate test or multivariate model perspective may be used (Arnau and Balluerka, 2003; Kowalchuk, Keselman and Algina, 2003).
If the repeated measures design is unbalanced and the covariance matrices are heterogeneous, the empirical literature indicates that both approaches cannot be recommended because of their lack of robustness. Algina and Oshima (1995) suggest using the Improved General Approximation (IGA) test developed initially by Huynh (1978) whereas Lix and Keselman (1995) proposed a Welch-James (WJ) type test based on the work of Johansen (1980). Based on the power results presented by Algina and Keselman (1998), the WJ test may be preferred over the IGA test, particularly when sample sizes are large enough to obtain a robust WJ test. On the other hand, Vallejo, Fidalgo, and Fernández (2001) recommend using the multivariate version of the modified Brown and Forsythe (BF, 1974) procedure. Their results indicate that the BF procedure provides a robust test of the within-subjects main and interaction effects, especially when the design is balanced or when group sizes and covariance matrices are positively paired.
Another more flexible approach to the analysis of repeated measurements, and particularly useful when sample size is the sufficiently large to support asymptotic inference, is the mixed linear model. Under this approach, implemented in commercial software packages, including the widely used SAS® program, researchers rather than presuming a certain type of covariance structure may model the structure before testing for treatment effects. For example, the best covariance structure can be selected based on Akaike’s Information Criterion (AIC) and/or Schwarz’s Bayesian Information Criterion (BIC) values for various potential covariance structures. According to advocates of the mixed-model approach, selecting the most parsimonious covariance structure possible is very important because this may result in more accurate and efficient inferences of the fixed-effects parameters of the model and consequently more powerful tests of the treatment effects. Nonetheless, when sample sizes are small it is known that the inference about the parameters in the mean structure can be inadequate, since the conventional estimate of covariance matrix of the regression parameters are only asymptotically valid (Wolfinger, 1996). In order to circumvent such problem Fai and Cornelius (1996) and Kenward and Roger (1997) have developed two different solutions that can be applied with any fixed and random effects model and covariance structure.
Recently, Keselman, Algina, Kowalchuk, and Wolfinger (1999) compared the multivariate WJ approach and the mixed-model Satterthwaite F tests based on work the Fai and Cornelius (1996), as obtained through the SAS (1996) Proc Mixed procedure, with regard to their power and robustness. Their results reveal that the Satterthwaite optional F test provides reasonably good protection against Type I errors when the correct structural model was known, and was slightly more powerful than the WJ procedure. However, Keselman et al. (1999) found that the Satterthwaite F-tests based on AIC or BIC were prone to liberal rates of Type I errors, mainly when group sizes and covariance matrices were negatively paired. Since researchers will not know the correct covariance structure, the authors suggested that the WJ approach is a viable procedure worth to the analysis of repeated measures data. However, for testing whether the pattern of change over time is the same across the groups, usually the most important for the research question investigated (Mass and Snijders, 2003), the WJ test does not necessarily control the Type I error rate; particularly when the sample sizes are not sufficiently large and the data are sampled from multivariate non-normal distributions (Algina and Keselman, 1997). Unfortunately, it is known that educational and behavioral research data will rarely follow a normal distribution (Micceri, 1989), and according to a recent survey by Keselman et al. (1998), large sample sizes are the exception rather than the norm in psychological investigations.
Accordingly, the purpose of the present study was to compare the Type I error and power rates of the multivariate version of the improved BF procedure and mixed-model approach for testing within-subjects main and interaction effects in a design with one grouping factor and one of repeated measures factor. The mixed model uses generalized least squares estimation of mean parameters and residual maximum likelihood for covariance parameters. The BF approach uses ordinary least squares computation based on a model in which random effects and dispersion matrix are treated as fixed and unstructured, respectively. Our goal is to determine whether both procedures provide similar results or favor the approach mixed-model based on the correct population covariance structure. The results corresponding to the mixed-model approach can be obtained with several software programs, however, we used the Kenward and Roger (1997; KR) residual df option available though SAS (2001) Proc Mixed. Since the mixed model approach allows the researchers to model the correct covariance structure, may be expected that provides more powerful tests of the fixed effects than the BF approach. Particularly, in those situations in which the covariance structure plays an important role in the estimation; however, this observation has no yet been confirmed through empirical investigation.
Description of the procedures to be compared
The linear model to the statistical analysis of repeated measures obtained from p groups of nj subjects (i,…, nj; ∑nj= n) at a common set of t occasions can be written as
yi= Xi β + εi (1)
where yi is an tx1 vector of t measurements observed on the ith experimental unit, Xi is a known txh design matrix; β is a hx1 vector of unknown population parameters; and εi is a tx1 vector of random errors. For inference purposes, it is assumed that the vector associated with the ith experimental unit, have a normal distribution with zero mean and dispersion matrix Σi. For example, in the repeated measures ANOVA mixed model, the referred suppositions imply a constant correlation between all pairs of observations on the same subject and homogeneous variances. In theory this approach can be useful for applications involving short time series per experimental unit, or when the response from each experimental unit is measured under multiples conditions rather than at multiple time points. Unfortunately, the practical experience suggests that there are many applications involving to collect multiple measurements on a subject that does not conform to the simple compound symmetry assumption.
Approach of the general linear mixed effects model
The mixed-effects model for repeated measures data extends the general linear model to cases where standard assumptions of independence and homogeneity are not required and where predictor variables are both continuous and categorical. This model, described by Laird and Ware (1982) to characterize the common structure of repeated measures, growth curve, or serial measurements data, can by written as
yi= Xi β + Zi ui + εi (2)
where yi= (yil,..., X'iti)’, β is a hx1 vector of unknown population parameters, ui is a kx1 vector of unknown subject-specific random effects, Zi=(Z’i1,…, Z’iti)’ and εi is a tix1 vector of unknown parameters whose elements don’t need to be independent neither homogeneous. Equation (2) defines the general linear mixed model, since Xi, Zi and Ri can be quite general. Specifically, the mixed model for repeated measures allows that the subjects can have different number of observations and that the time intervals can be unique for each subject. It also permits to modeling between-subjects and within-subjects variation, for complete as well as for incomplete data.
The distributional assumptions for model (2) are that ui and εi are independent random vectors distributed as ui ~ N (0,G) and εi ~ N (0,Ri), respectively. Here G is a positive definite kxk matrix of unknown covariance parameters for the between-subjects random effects, and Ri is a tixti positive definite covariance matrix for the within-subject errors. These assumptions imply that the observations vectors y1,…, yn are independent N (Xi, Β, Vi(θ)), where Vi(θ)= Zi GZ’i+Ri. The covariance matrix Vi(θ) is assumed to be a function of a vector of q unknown variance-covariance parameters. If G is diagonal, each Zi consists of only ones and zeros, and Ri= σ2Ii, then the general linear mixed model reduces to the ANOVA mixed model. Also the usual general linear model is obtained setting Zi= 0 and Ri= σ2Ii. The combined model for all of the data may be obtained by stacking the vectors yi, ui, εi, and the matrices Xi respectively, and letting Z= diag (Z1,… Zn), G = diag (G,…, G), and R= diag (R1,… Rn).
When all covariance parameters are known, the standard estimators for Β and u can be obtained solving the so-called mixed model equations presented by Henderson (1975). Specifically, the solutions can be written as
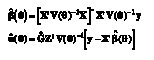 (3)
(3)
and the variance-covariance matrices of the corresponding estimators are
where the minus sign indicates that a generalized inverse is required if X doesn’t have full rank and P= V(θ)-1 – V(θ)-1X[X’V-1(θ)X]–X’V(θ)-1. The vector θ contains the unique elements of G ~ and the parameters in R.
Equation (4) provides the machinery for testing hypotheses about fixed (Β) and random (u) effects. For example, to test the null hypothesis H0: LΒ= 0, where L is an estimable contrast matrix, we can derive an approximate F statistic dividing the Wald test by the numerator df and approximating the denominator df. Under H0, the test statistic
F = 1 / R (L){β' L'[L(X' V-1 (θ) X)- L']-1 Lβ^} (5)
follows approximately an F-distribution with ν1 numerator and ν2 denominator df. The numerator df for the approximating F distribution are the rank of L, but the denominator df needs to be estimated from the data.
Unfortunately, the matrices G and R hardly ever are known. Consequently, an estimate V(θ^) of V(θ) must be used in the computation of the equations (3)-(5). Although the literature referred to the estimation of variance components for a general linear mixed model is extensive (see Harville 1977 for an excellent review), in practice, a variant of maximum likelihood estimation known as residual maximum likelihood (REML) estimation is often used to estimate V(θ) (Zimmerman and Núñez-Antón, 2001). Once the dispersion matrix has been selected and its parameters conveniently estimated through the REML approach, we estimate Β as in (3), but with V(θ) replaced by the solution V(θ^) and testing the hypotheses about the fixed effects by using approximate F- statistics.
When an estimate V(θ^) of V(θ) is used in the computation of ß the resulting estimator is often called as estimated generalized least squares (EGLS) estimator and we shall denote it as Β ^. The EGLS estimator of Β is unbiased and fully efficient if the true variance of Β ^, V(Β ^), correctly specified the asymptotic dispersion matrix; that is, if V(Β ^)= [X’V-1(θ)X]–. However, if V(Β ^)π V(ß ^) the EGLS estimator of Β is still unbiased, but no fully efficient, and the estimated asymptotic covariance matrix of Β ^, [X’V-1(θ)X]–, is not valid estimate of V(Β ^) (Littell, 2002). In practice, this supposes that the likelihood-based inference should be interpreted with care when the sample size is not sufficiently large, since [X’V-1(θ^)X]– is not always a good estimated of true V(Β ^). Kenward and Roger (1997) provide an adjusted estimator of the covariance matrix of ß that has reduced bias for small sample inference when the asymptotic covariance matrix underestimates V(ß ^). The method provides an adjusted dispersion matrix of the fixed effects, with appropriate scaling of Wald statistics and associated denominator degrees of freedom for the approximating F distribution obtained via a Satterthwaite-type approximation (Verbeke and Molenberghs, 2000). This methodology, implemented as option into computation of standard errors and test statistics in the Mixed procedure of SAS, will be used in this study. Another way to deal with the underestimation of standard errors is through the sandwich variance estimator for V(Β ^) suggest by Liang and Zeger (1986).
Multivariate Brown-Forsythe (BF) test modified
To test the hypothesis of equality of p means when the population variances are unequal, Brown and Forsythe (1974) proposed the statistic
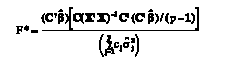 (6)
(6)where σ^2j= y’j[I–X(X’X)-1X’]yj and cj= (1–nj/n). They suggested that F*, be approximated by the distribution F (p–1, ν), where
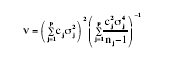 (7)
(7)
is determined using Satterthwaite’s (1941) method.
However, Rubin (1983) and Mehrotra (1997) have shown that the approximation proposed by BF for the null distribution of their test statistic is inadequate, and they suggest Box’s (1954) method to approximate the distribution of F* with the distribution F (ν1, ν2), where
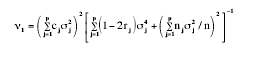 (8)
(8)
v2= v of (7) and rj= nj/n.
Vallejo and Escudero (2000) and Vallejo et al. (2001) extended the BF statistic to the doubly multivariate setting replacing means by corresponding mean vectors and replacing variances by corresponding dispersion matrices. Applying their approach, the statistics used to test the hypothesis concerning to the within-subjects interaction are functions of the eigenvalues of HE*-1, where H
H = (C' BÂ)' [ C' ( C' (X' X) - C]-1 (C' BÂ) (9)
and
and B^ is the ordinary least squares solution to the
normal equations, for C’= [1p-1:–1] and A’= [It-1:–1].
This form of E* ensures that the expected values of H and the
expected value of ![]() are
equal when the null hypothesis is true, since mean vectors are being compared
across groups.
are
equal when the null hypothesis is true, since mean vectors are being compared
across groups.
Using results in Nel and van der Merwe (1986), the distribution
of ![]() can be approximated as a sum of Wishart distributions
can be approximated as a sum of Wishart distributions
![]() (11)
(11)
with df
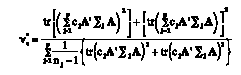 (12)
(12)The df are estimated substituting Σj for Σ^j within summation on the right-hand side.
Having computed the matrices E* and H any of the usual multivariate criteria can be used for testing the primary hypothesis of interest (see Timm, 2002, pp. 102-103). In our investigation this hypothesis was tested using the F-test approximation to Wilk’s Δ given by Rao (1951) as
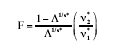 (13)
(13) where s*= [(l2 v*2h–4) / (l2+v*2h–5)1/2, v*1= lv*h, and v*2= [v*e – (l–v*h + 1) / 2]s* – (lv*h – 2) / 2, with l equal to the dimension of E* and ν*h equal to
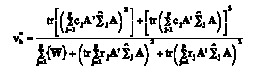 (14)
(14) where W= [(tr A’Σ^jA)2 + tr (A’Σ^jA)2] – 2rj[(tr A’Σ^jA)2 + tr (A’Σ^jA)2]. The hypothesis interaction is rejected at nominal α if F > F(1–α);v*1, v*2, where F(1–α);v*1,v*2 is the 100 (1–α) th percentile of the F-distribution with v*1 and v*2 df.
The modification of numerator df was determined by solving
simultaneously the equations ![]() and
and ![]() ,
after assuming that the distribution of H, under inequality of covariance
matrices, is a sum of Wishart variables. Specifically, we assume that (a) random
effect has the same expected value as that of the effect under consideration,
when the null hypothesis is true, (b) the distribution of H is a weighted
sum of Wishart variables, (c) each Wishart distribution in the sum has one degree
of freedom, and (d) the weights are the same as the weights in the sum of chi-squares
variables of the numerator of ANOVA F-test when the variances are heterogeneous.
For more details the readers are referred to the work of Khatri (1980).
,
after assuming that the distribution of H, under inequality of covariance
matrices, is a sum of Wishart variables. Specifically, we assume that (a) random
effect has the same expected value as that of the effect under consideration,
when the null hypothesis is true, (b) the distribution of H is a weighted
sum of Wishart variables, (c) each Wishart distribution in the sum has one degree
of freedom, and (d) the weights are the same as the weights in the sum of chi-squares
variables of the numerator of ANOVA F-test when the variances are heterogeneous.
For more details the readers are referred to the work of Khatri (1980).
The statistics used to test the repeated measures main effect averaged over groups hypothesis, can be expressed in terms of the matrices H~ and E~, where
H~= (C' B~A)' [C' (X' X)- C]-1 (C' B~A) (15)
and
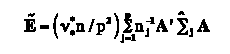 (16)
(16)
To test this hypothesis, the A matrix defined to test
the interaction effect is used and the C’ matrix is a 1 x p
vector of ones. In (15), ![]()
Extending the results reported by Nel and van der Merwe (1986),
the distribution of ![]() can be approximated as a sum of Wishart distributions
can be approximated as a sum of Wishart distributions
![]() (17)
(17)
with df
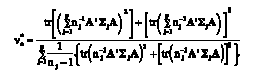 (18)
(18)
Next, the hypothesis of no occasions main effect can also be rejected approximately if
where s= [(l2v2h– 4) / (l2 + v2h– 5)]1/2, v1= l vh, and v*2= [v*e – (l – vh + 1) / 2] s – (l vh – 2) / 2.
Monte Carlo Study
In order to determine the viability of the mixed model test with KR solution and the modified BF test for controlling the rate of Type I errors, a Monte Carlo investigation was conducted utilizing a design that had one between-subjects factor (p= 4) and one within-subjects factor (t= 4). Five variables were manipulated: (a) total sample size, (b) degree of group size inequality, (c) nature of the pairing of the covariance matrices and group sizes, (d) type of covariance matrices, and (e) distributional shape of the data.
The behaviour of the test statistics was investigated with
two total sample size conditions: n= 30 and n= 45. These sample
sizes were selected because they are typical of what is encountered in practice,
particularly in areas such as animal psychology, applied behaviour analysis,
and clinical psychology. Within each of these sample size conditions, both a
moderate and severe degree of group size inequality were investigated, as indexed
by a coefficient of sample size variation (Δ). For n= 30, the group
sizes were: 8, 10, 12 (Δ= .16) and 6, 10, 14 (Δ= .33). Whereas for
n= 45, the group sizes were: 12, 15, 18 (Δ= .16) and 9, 15, 21
(Δ= .33), where ![]() and n– is the average group size.
and n– is the average group size.
The fifth variable investigated in this study was pairing
condition. Null, positive and negative pairing of group sizes and covariance
matrices were investigated. A null pairing refers to the case in which the design
is balanced, that is, the size of the element values of the covariance matrices
were not related with the group sizes because all groups had equal size. A positive
pairing refers to the case in which the largest nj was associated
with the covariance matrix containing the largest element values; a negative
pairing refers to the case in which the largest nj was associated
with the covariance matrix containing the smallest element values. In all conditions
![]()
The fourth variable investigated was the pattern of covariance structure. In the present work, the three following homogeneous and heterogeneous first-order autoregressive (AR) models were manipulated:
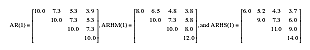
The homogeneous first-order autoregressive [AR(1)] model specify equal response variances and the correlation decreases as the distance between the time points increases. This model requires only two parameters to be estimated because the variances along the main diagonal are constant and the covariances decline exponentially. The first-order autoregressive [ARHM(1) and ARHS(1)] models are considered heterogeneous structures because the response variances increase over time and the covariances decline exponentially (see Núñez-Antón and Zimmerman 2001 for additional details). Both structures require five parameters to be estimated, but the degree of heterogeneity the ARHS(1) is substantially greater than the ARHM(1). The three structures had a similar departure from sphericity pattern (ε≡.75) and also a similar correlation pattern (p≡.73).
The fifth variable investigated was the distributional shape of the response variable. This factor had two levels: Multivariate normal and multivariate non-normal. Using the Proc IML program from SAS (SAS Institute, 2001), data were simulated to conform to each of the conditions investigated. With respect to the former condition, for each level of the between-subjects factor, we generated vectors of pseudo-random normal variates using the RANNOR function in SAS. The multivariate observations were obtained by the method via triangular decomposition (see Fernández and Vallejo, 2002). The non-normal data were generated using the multivariate extension of the Fleishman (1978) power method developed by Vale and Maurelli (1983). The skewed distribution was a chi-squared standardized distribution with skewness (γ1) and kurtosis (γ2) values 1.63 and 4, respectively. This particular type of non-normal distribution was selected since the empirical literature indicates that tests of significance of the repeated measures effects might not perform optimally when covariance matrices are heterogeneous and data are sampled from skewed moderately distributions in unbalanced designs (Algina and Keselman, 1997). Programming used in this study to generate non-normal data had been scrutinized and verified for accuracy, and can be obtained free of charge written in the GAUSS (Aptech Systems, 1996) language from Nevitt and Hancock (1999). A SAS/IML program also is available from the first author’s. The program only requires entering the desired population skewness and kurtosis to derive the Fleishman power transformation constants, the sample size, and the population covariance matrices for the data.
The second phase of our study compared the power of the mixed
model approach with KR solution and the BF test to detect the within-subjects
main and interaction effects under conditions where both procedures reasonably
controlled their rates of Type I error. Six factors were manipulated in this
second phase of the investigation. Total sample size, relationship between group
sizes and dispersion matrices, degree of group size inequality, type of covariance
matrices, and shape of underlying distribution were the same as those used in
the Type I error phase. The sixth factor investigated, was the permutation of
the mean vector. Based on the work of Algina and Keselman (1998), the following
six permutations were included in each of the three groups of the design: (μ,
μ, 0, 0), (0, -μ, μ, 0), (0, 0, -μ, μ), (0, -μ, 0, μ),
(-μ, 0, 0, μ), and (-μ, 0, μ, 0). When interest lay in estimating
power to detect the main effect, each group was assigned the nonzero mean vector.
When interest lay in estimating power to detect the interaction effect, only
the first group had a nonzero mean vector; while the remaining groups were assigned
the null vector; moreover, in this case two levels of dispersion inequality
were used: ![]() and
and ![]() .
For each sample size one value of μ was selected to give a .80 power value
for Scheffé’s univariate mixed model. We employed the SAS functions FINV
and FNONCT to find the noncentrality parameters (λ) such that Prob[F(v1,v2,λ)>;F.05(v1,v2,0)]=0.80
for the within-subjects main and interaction effects. There is no reason to
believe that the results differ essentially for other nominal powers.
.
For each sample size one value of μ was selected to give a .80 power value
for Scheffé’s univariate mixed model. We employed the SAS functions FINV
and FNONCT to find the noncentrality parameters (λ) such that Prob[F(v1,v2,λ)>;F.05(v1,v2,0)]=0.80
for the within-subjects main and interaction effects. There is no reason to
believe that the results differ essentially for other nominal powers.
Lastly, we developed a SAS macro program to carry out the calculations corresponding to the BF test and the KR test in conjunction with Proc Mixed. This operation allows comparing the performance of the techniques in connection with each one of the manipulated variables. Empirical Type I error rates were collected by dividing the number of times each statistic exceeded its critical value when the mean vector was the null vector by the number of made executions. Empirical power rates were collected by dividing the number of times each statistic exceeded its critical value when the mean vector was the non-null vector by the number of made executions. One thousand replications of each condition were performed using a .05 significance level.
Results
In order to help identify conditions when the tests are robust and when they are not, we set a criterion that the empirical alpha level would have to deviate from the nominal by more than two standard errors (SE). The SE was calculated using [α(1– α)/1000]1/2, where α is the nominal level of significance and 1000 is the number of replications. According to this criterion, in order for a test to be considered robust, its empirical rate of Type I error (α^) must be contained in the interval (.036 ≤ α^ ≤ .064) for the 5% level of significance. Correspondingly, a test was considered to be non-robust if, for a particular condition, it’s Type I error was not contained in this interval. In the tables values which differ significantly (±2 SE) from the nominal level are in bold face type. Tests with empirical estimates that are significantly lower that the nominal alpha level are referred to as conservative, while those whose rates are significantly higher are referred to as liberal. In connection with the method of identifying a non-robust procedure, it should be pointed out that several standards have been used by researchers to identity nonrobust procedures (see, Bradley, 1978; Mehta and Srinivasan, 1970). Therefore, it should be noted that with other standards different interpretations of the results are possible. To evaluate power, the two procedures were compared to each other under alternative hypothesis when both procedures resulted in comparable Type I error control. Pavur and Nath (1978) recommend estimating powers using empirical critical values and nominal critical values.
Type I Error Rates for Tests of the Occasions Main Effect
Normally Distributed Data. Table 1 contains the empirical rates of Type I error for the main effect when data were obtained from a multivariate normal distribution.
As seen from Table 1, the Type I error rate was well controlled with both procedures. In particular, the Proc Mixed with KR solution was able to control the Type I error rates across all of the investigated conditions, except for the negative pairing condition when n= 30 and Δ= .33. Similar results were obtained with the BF procedure. At any case, there was a for tendency, the KR solution and the BF procedure to be slightly conservative, which tended to decline as the sample sizes increased. The pattern of covariance matrices had little effect on the results associated with both procedures.
Nonormally Distributed Data. Table 1 also contains the empirical rates of Type I error for the main effect when data were sampled from a multivariate non-normal distribution. As seen from Table 1, the KR rates were contained within the ±2 SE bounds of a when heterogeneous covariance matrices were paired with equal groups sizes or when the pairing pattern was positive. The results obtained for the negative pairing conditions, however, were slightly conservative, especially when Δ= .33. Similarly, the BF test also was prone to deflated rates of Type I error for negative pairings. Nevertheless, the conservative tendency of the two tests tends to decline as the sample sizes increases and the magnitude of Δ decreases. The comparison of Type I error rates indicates that the Proc Mixed with KR solution maintained α^ at the nominal level in 22 out of 30 possible conditions, whereas for the BF test the number of statistically significant deviations from the nominal alpha level was three.
Contrary to what happened when data were sampled from a multivariate normal distribution, the pattern of covariance matrices had a superior effect on the robustness of both procedures. When the data were obtained under the ARHS(1) covariance structure, Type I error rates increased for both procedures. However, when the data were obtained under the AR(1) and ARHM(1) covariance structures, Type I error rates decreased for the both procedures. For example, the value of α^ averaged across all sample sizes and five values of Δ were .036 and .038 under condition ARHM(1), respectively, for the Proc Mixed with KR solution and the BF procedure, whereas under condition ARHS(1) they were .042 and .048, respectively.
Type I Error Rates for Tests of the Groups by Occasions Interaction Effect
Normally distributed data. Table 2 contains Type I error rates for the test of the interaction effects when data were sampled from a multivariate normal distribution.
An inspection of the results in Table 2 indicates that, the BF statistic was able to control the Type I error rate across all of the investigated conditions. Again, the procedure had a tendency to be conservative when the pairing pattern was negative. Also, the degree of conservativeness decreased with increases in the total sample size and with decreases in the magnitude of Δ. On the other hand, the Proc Mixed with KR solution Type I error rates was similar to those reported for the main effects hypothesis. However, for null, positive and negative pairing, error rates were generally lower than those obtained for the within-subjects main effect. In this case, the degree of conservativeness of the procedure also decreased as the sample sizes increased. Thus, when n= 30 the value of α^ averaged across covariance matrices and values of Δ was .038, whereas for n= 45 the average valor was .042. Finally, pattern of covariance matrices had little effect on the results associated with both procedures.
Nonnormally distributed data. Table 2 also contains the empirical rates of Type I error for the interaction effect when data were sampled from a multivariate non-normal distribution. The Proc Mixed with KR solution and the BF procedure did not provide a robust test across all investigated conditions. Specifically, the KR rates were always conservative, especially when covariance matrices and group sizes were negatively paired. On the other hand, the BF test had the fewest number of significant deviations from the nominal alpha level, even though its rates were conservative in more than half of the examined conditions. In this case, the empirical Type I error rate averaged across all of the investigated conditions was α^= .035, with the degree of conservativeness decreasing with increases in the total sample size.
A careful examination of the Table 2 also reveals that, contrary to what happened when data were sampled from a multivariate no-normal distribution for the main effects test, pattern of covariance matrices had little effect on the robustness of both procedures.
Power Rates for Tests of the Occasions Main Effect
Normally distributed data. We are assuming that power comparisons between tests procedures are only of concern when test statistics provide reasonable Type I error protection. Power rates estimates, averaged across sample sizes for the main effect, are reported in Table 3.
The results presented in Table 3 indicate that the Proc Mixed with KR solution was uniformly more powerful than the BF procedure. In fact, an examination of Table 3 reveals that KR solution has the highest power for 81 of the 90 conditions investigated. The discrepancies between the BF test and the KR solution tends to increase when covariance matrices and group sizes were negatively paired, and to decrease when they were positively paired. When the pairing pattern was positive, the power advantage never exceeded 2 percentage point on average. However, when the pairing pattern was negative the mean power value for the KR solution exceeded the BF power by more than 9 percentage points. In this case, the largest power difference between the procedures was .095, which occurred for the (0, -μ, μ, 0) and ARHM(1) covariance structure case.
The results also show that the pattern of power of the Proc Mixed with KR solution and the BF test tended to increase slightly as the type of covariance structure changed from ARHS(1) to ARHM(1) and then to the AR(1) condition, especially, for the (0, -μ, μ, 0), (0, 0, -μ, μ), and (0, -μ, 0, μ) permutations. Furthermore, the power estimates for both the KR and BF tests were strongly affected by the pairing conditions and the effect of permutation of the mean vector. In the former case, the power rates tended to increase when covariance matrices and group sizes were positively paired, and decreased when they were negatively paired. In the later case, greater power occurred for the (0, -μ, μ, 0) permutation, and the less power occurred for the (-μ, 0, 0, μ) permutation.
Nonnormally distributed data. Table 4 contains the empirical power rates averaged across sample sizes for the main effect when data were obtained from a non-normal distribution.
The results presented in Table 4 indicate that the pattern of power differences between both tests was similar to those reported in Table 3. That is, the KR solution was, in general, more powerful that the BF test. In this case, the KR solution had the highest power for 76 of the 90 conditions investigated. The effect of non-normality on power differences was small. Thus, for the ARHS(1) condition, the average KR and BF power rates (averaging over the six permutations) were .665 and .644, respectively for the normal distribution and .686 and .666 for the non-normal distribution, respectively. For the negative pairing conditions, power rates associated with the skewed distribution were generally larger than obtained for the normal data counterparts. On the other hand, for positive pairing conditions, the empirical power values associated with the skewed distribution were not always larger than those obtained when data were obtained from the normal distribution. Furthermore, as was true for the main effect test and normally distributed data, pattern of covariance matrices had a small effect on the results associated with both procedures. However, the power of both tests was seriously affected by the effect of permutations of the mean vector and the patterns of pairings. In particular, power values for the KR solution and the BF test were greatest for the (0, -μ, μ, 0) permutation and for positive pairings and lowest for the (-μ, 0, 0, μ) permutation and for negative pairings.
Power Rates for Tests of the Groups by Occasions Interaction Effect
Adequate power comparisons can only be made between procedures giving comparable Type I error, and the Proc Mixed with KR solution had an excessively conservative behavior when data were sampled from a multivariate non-normal distribution. Thus, it is important to be clear that the following comments only pertain to the interaction effects when data were sampled from a multivariate normal distribution. Power estimates, averaged across total sample size, are presented in Table 5 for five patterns of pairings, two relationships between the degree of group size inequality and dispersion matrices, and six permutations of the mean vector. In this case, all estimates correspond to the first-order autoregressive structure. Based on the power results obtained for the occasions main effect, there is no reason to believe that the results would differ dramatically for the ARHM(1) and ARHS(1) covariance structures.
The averaged power rates presented in Table 5 for the tests
of interaction when the group with the mean vector non-null had the smallest
variance ![]() were
qualitatively similar to those for the tests of the main effect. That is, the
Proc Mixed with KR solution was always more powerful than the BF procedure.
Under this condition, the mean power value for the KR solution exceeded the
BF power by more than 22 percentage points. Specifically, the empirical power
rates averaged across all of the investigated conditions were .812 and .661,
respectively for the mixed model and BF approaches. When
were
qualitatively similar to those for the tests of the main effect. That is, the
Proc Mixed with KR solution was always more powerful than the BF procedure.
Under this condition, the mean power value for the KR solution exceeded the
BF power by more than 22 percentage points. Specifically, the empirical power
rates averaged across all of the investigated conditions were .812 and .661,
respectively for the mixed model and BF approaches. When ![]() the results also indicated that the Proc Mixed with KR solution was more
powerful than the BF procedure in most cases. In fact, an examination of Table
5 reveals that the KR solution has the highest power for 28 of the 30 conditions
showed; in addition, when the BF test was more powerful the power advantage
never exceeded 1 percentage point on average. Nevertheless, both the large power
and the large differences between the Proc Mixed with KR solution and
the BF tests occur mainly when
the results also indicated that the Proc Mixed with KR solution was more
powerful than the BF procedure in most cases. In fact, an examination of Table
5 reveals that the KR solution has the highest power for 28 of the 30 conditions
showed; in addition, when the BF test was more powerful the power advantage
never exceeded 1 percentage point on average. Nevertheless, both the large power
and the large differences between the Proc Mixed with KR solution and
the BF tests occur mainly when ![]() and
are much larger for some permutations than for others.
and
are much larger for some permutations than for others.
Discussion and recommendations
The purpose of this investigation was to compare the performance of the modified BF approach presented by Vallejo et al. (2001) with the performance of the SAS (2001) Proc Mixed procedure based on Kenward and Roger’s (1997) approximation when testing within-subjects main and interaction effects in unbalanced repeated measures designs. Specifically, we examined the robustness and power of these procedures when the between-subjects covariance matrices were heterogeneous and the simulated data were obtained from the multivariate normal or multivariate non-normal distributions.
The results indicate that when the normality and homogeneity assumptions are jointly violated, both the Proc Mixed with KR solution and the BF procedure exhibited good control of Type I error rates across all of the investigated conditions for the within-subjects main effect. Furthermore, it should be pointed out that a similar pattern of results was obtained with both procedures. Specifically, for negative pairings of covariance matrices a very unequal group sizes, the behaviour of both procedures was slightly conservative. Under this condition, however, the KR solution was more powerful than the BF test, and its advantage was sometimes appreciable. On the other hand, when the design was balanced or the pairing pattern of group sizes and covariance matrices was positive, the empirical power values were very similar between both approaches. Moreover, there were some conditions in which the BF test was more powerful than the KR solution. Consequently, when the design is balanced or the pairing pattern of group sizes and covariance matrices is positive, these results suggest that there will be no appreciable loss in power if the Proc Mixed with KR solution or the BF test is used. However, users can easily implement via SAS.
With regard to the test of the interaction effect, our results indicate that the KR solution can in most cases effectively control the rate of Type I errors when group variance-covariance matrices are heterogeneous and the data are obtained from a multivariate normal distribution. The procedure tends to be slightly conservative when the data are non-normal in form, especially, for negative pairings covariance matrices a sample sizes and substantial values of coefficient of sample size variation. On the other hand, the BF test also provided good Type I error control when the multivariate normality assumption is satisfied. However, the approach tends to be conservative when the data are sampled from a skewed distribution and the total sample was small. Fortunately, consistent with the findings of Lix, Algina, and Keselman (2003) and Vallejo et al. (2001), the conservative tendency of the both tests tends to decline as the sample sizes increases and the magnitude of Δ decreases. In connection with the power, it is interesting to note that in some cases there were differences between both procedures in favour of the KR solution. In particular when the group with the nonzero mean vector was associated with the smallest variance and covariance matrices were negatively paired with group sizes.
In summary, the results of this investigation shows that the two procedures examined were able to control the rate of Type I errors in most of the investigated conditions, but the Proc Mixed with KR solution was generally more powerful than the BF test. Nevertheless, the power advantages were small for null and positive pairings conditions. Furthermore, the reader should be note that the KR solution was utilized in a situation in which the correct covariance structures are known in advance. That is, in the simulations, the Proc Mixed with KR solution was implemented such that the form of the true covariance structure matched exactly that used the mixed-model analysis. In practice, applied researchers determine the appropriate covariance structure of their data through some of the criteria implemented in commercial software packages (p.e., AIC). However, such selection is one the main difficulty in parametric analysis of longitudinal data (Galecki, 1994; Keselman, Algina, Kowalchuk and Wolfinger, 1998). Moreover, Keselman et al. (1999) using the mixed-model Satterthwaite F test computed by SAS (1996) Proc Mixed program, found that the Akaike criterion was prone to elevated rates of Type I error for negative pairings. Thus, our BF results may be most promising for applied researchers who would not know the true covariance structure at their data.
Although the generality of our results is limited by the range of conditions and parameter sets employed in the simulations, therefore other conditions or other parameter sets could give different results. In our opinion, when all subjects have complete response vectors a general recommendation can be made. The applied researchers should be comfortable using the modified BF test to analyze longitudinal data hypotheses when the assumptions of the general linear model are violated, since they need neither to model their data nor to rely on methods that typically selected an incorrect covariance structure. It should be pointed out, however, that the BF method can be inefficient in those situations in which the covariance structure plays an important role in the estimation, just the situations where the Proc Mixed with KR solution has far greater power. However, the need to estimate the covariance structure makes the mixed model approach less attractive with an unstructured matrix or when the sample sizes are small.
As a final note, three lines of additional research can be of interest. First, it is very important to investigate whether the modified BF procedure offers robust and powerful tests when covariance matrices vary across groups, but are not multiples of one another. Second, additional research manipulating other types of the parametric covariance structures and other types of non-normal distributions, both symmetric and asymmetric distributions with light tail and heavy tail, might also be investigated. For example, it would be desirable to know the operating characteristics of the KR method if, say, TYPE= TOEP or TYPE= UN is used in the Proc Mixed code and the covariance structure is selected based on an AIC or BIC criterion. Finally, would be useful to extend the BF approach to more complicated kinds of measures repeated designs, including situations in which some subjects have incomplete response vectors over time.
Acknowledgments
This work was supported by MCYT grant BOS-2000-0410 and by FICYT grant PR-01-GE-2.
The authors wish to thank the professor Vicente Núñez-Antón for valuable comments and insightful suggestions.
In order to help identify conditions when the tests are robust and when they are not, we set a criterion that the empirical alpha level would have to deviate from the nominal by more than two standard errors (SE). The SE was calculated using [α(1– α)/1000]1/2, where α is the nominal level of significance
Algina, J. and Keselman, H.J. (1997). Testing repeated measures hypotheses when covariance matrices are heterogeneous: Revisiting the robustness of the Welch-James test. Multivariate Behavioral Research, 32, 255-274.
Algina, J. and Keselman, H.J. (1998). A power comparison of the Welch-James and Improved General Approximation tests in the split-plot design. Journal of Educational and Behavioral Statistics, 23, 152-169.
Algina, J. and Oshima, T.C. (1995). An improved general approximation test for the main effect in a split-plot design. British Journal of Mathematical and Statistical Psychology, 48, 149-160.
Aptech Systems Inc. (1996). The Gauss System and Graphics Manual (Version 3.2.31). Maple Valley Washington: Aptech Systems, Inc.
Arnau, J. and Balluerka, N. (2003). Longitudinal and growth trajectory data analysis. Traditional approach and current proposals. Psicothema, 16, 156-162.
Box, G.E.P. (1954). Some theorems on quadratic forms applied in the study of analysis of variance problems, I. Effects of inequality of variance in the one-way classification. Annals of Mathematical Statistics, 25, 290-403.
Bradley, J.V. (1978). Robustness? British Journal of Mathematical and Statistical Psychology, 31, 144-152.
Brown, M.B. and Forsythe, A.B. (1974). The small sample behavior of some statistics which test the equality of several means. Technometrics, 16, 129-132.
Fai, A.H.T. and Cornelius, P.C. (1996). Approximate F-tests of multiple degree of freedom hypotheses in generalized least squares analyses of unbalanced split-plot experiments. Journal of Statistical Computation and Simulation, 54, 363-378.
Fernández, P. and Vallejo, G. (2002). Absence of normality and groups size inequality. Does it affect to autocorrelation estimation? Psicothema, 14, 497-503.
Fleishman, A.I. (1978). A method for simulating nonnormal distributions. Psychometrika, 43, 521-532.
Galecki, A.T. (1994). General class of covariance structures for two or more repeated factors in longitudinal data analysis. Communications in Statistics-Theory and Methods, 23, 3.105-3.119.
Harville, D.A. (1977). Maximum likelihood approaches to variance component estimation and to related problems. Journal of the American Statistical Association, 72, 320-338.
Henderson, C.R. (1975). The best linear unbiased estimation and prediction under a selection model. Biometrics, 31, 423-447.
Huynh, H. (1978). Some approximate tests for repeated measurement designs. Psychometrika, 43, 161-165.
Johansen, S. (1980). The Welch-James approximation of the distribution of the residual sum of squares in weighted linear regression. Biometrika, 67, 85-92.
Kenward, M.G. and Roger, J.H. (1997). Small sample inference for fixed effects from restricted maximum likelihood. Biometrics, 53, 983-997.
Keselman, H.J., Algina, J., Kowalchuk, R.K. and Wolfinger, R.D. (1998). A comparison of two approaches for selecting covariance structures in the analysis of repeated measurements. Communications in Statistics-Simulation and Computation, 27, 591-604.
Keselman, H.J., Algina, J., Kowalchuk, R.K. and Wolfinger, R.D. (1999). The analysis of repeated measurements: A comparison of mixed-model Satterthwaite F tests and a nonpooled adjusted degrees of freedom multivariate test. Communications in Statistics-Theory and Methods, 28, 2.967-2.999.
Keselman, H.J., Huberty, C.J., Lix, L.M., Olejnik, S., Cribbie, R.A., Donohue, B., Kowalchuk, R.K., Lowman, L.L., Petosky, M.D., Keselman, J.C. and Levin, J.R. (1998). Statistical practices of educational researchers: analyses of their ANOVA, MANOVA, and ANCOVA analyses. Review of Educational Research, 68, 350-386.
Khatri, C.G. (1980). Quadratic forms in normal variables. In Handbook of Statistics 1: Analysis of Variance (P. R. Krisnaiah, Ed.). New York: North Holland, 443-466.
Kowalchuk, R.K., Keselman, H.J. and Algina, J. (2003). Repeated measures interaction test with aligned ranks. Multivariate Behavioral Research, 38, 433-461.
Laird, N.M. and Ware, J.H. (1982). Random-effects models for longitudinal data. Biometrics, 38, 963-974.
Liang, K.R. and Zeger, S. (1986). Longitudinal data analysis using generalized linear models. Biometrika, 73, 13-22.
Lix, L.M., Algina, J. and Keselman, H.J. (2003). Analysing multivariate repeated measures designs: A comparison of two approximate degrees of freedom procedures. Multivariate Behavioral Research, 38, 403-431.
Lix, L.M. and Keselman, H.J. (1995). Approximate degrees of freedom tests: A unified perspective on testing for mean equality. Psychological Bulletin, 117, 547-560.
Littell, R.C. (2002). Analysis of unbalanced mixed model data: A case study comparison of ANOVA versus REML/GLS. Journal of Agricultural, Biological, and Environmental Statistics, 7, 472-490.
Maas, C.J.M. and Snijders, T.A.B. (2003). The multinivel approach to repeated measures for complete and incomplete data. Quality and Quantity, 37, 71-89.
Mehrotra, D.V. (1997). Improving the Brown-Forsythe solution to the generalized Behrens-Fisher problem. Communication in Statistics-Simulation and Computation, 26, 1.139-1.145.
Mehta, J.S. and Srinivasan, R. (1970). On the Behrens-Fisher problem. Biometrika, 57, 649-655.
Micceri, T. (1989). The unicorn, the normal curve, and other improbable creatures. Psychological Bulletin, 92, 778-785.
Nel, D.G. and van der Merwe, C.A. (1986). A solution to the multivariate Behrens-Fisher problem. Communications in Statistics-Theory and Methods, 15, 3.719-3.735.
Nevitt, J. and Hancock, D.G. (1999). PWRCOEFF & NNORMULT: A set of programs for simulating multivariate nonnormal data. Applied Psychological Measurement, 23, 54.
Núñez-Antón, V. and Zimmerman, D.L. (2001). Modelización de datos longitudinales con estructuras de covarianza no estacionarias: Modelos de coeficientes aleatorios frente a modelos alternativos. Qüestiió, 25, 225-262.
Pavur, R. and Nath, R. (1989). Power and Type I error Rates for Rank-Score MANOVA Techniques. Multivariate Behavioral Research, 24, 477-501.
Rao, C.R. (1951). An asymptotic expansion of the distribution of Wilks’s criterion. Bulletin of the International Statistical Institute, 33, Part 2, 177-180.
Rubin, A.S. (1983). The use of weighted contrast in analysis of models with heterogeneity of variance. Proceedings of the Business and Economic Statistics Section, American Statistical Association, 347-352.
SAS Institute Inc. (1996). SAS/STAT Software: Changes and Enhancements through Release 6.11. Cary, NC: SAS Institute Inc.
SAS Institute Inc. (2001). SAS/STAT Software: Version 8.2 (TS M0). Cary, NC: SAS Institute Inc.
Satterthwaite, F.F. (1941). Synthesis of variance. Psychometrika, 6, 309-316.
Scheffé, H. (1956). A mixed model for the analysis of variance. Annals of Mathematical Statistics, 27, 23-36.
Timm, N.H. (2002). Applied Multivariate Analysis. Springer-Verlag: New York.
Vale, C.D. and Maurelli, V.A. (1983). Simulating multivariate nonnormal distributions. Psychometrika, 48, 465-471.
Vallejo, G. and Escudero, J.R. (2000). An examination of the robustness of the Brown-Forsythe and the Welch-James tests in multivariate split-plot designs. Psicothema, 12, 701-711.
Vallejo, G., Fidalgo, A.M. and Fernández, P. (2001). Effects of covariance heterogeneity on three procedures for analysing multivariate repeated measures designs. Multivariate Behavioral Research, 36, 1-27.
Verbeke, G. and Molenberghs, G. (2000). Linear Mixed Models for Longitudinal Data. Springer-Verlag: New York.
Wolfinger, R.D. (1996). Heterogeneous variance-covariance structures for repeated measures. Journal of Agricultural, Biological, and Environmental Statistics, 1, 205-230.
Zimmerman, D.L. and Núñez-Antón, V. (2001). Parametric modeling of growth curve data: An overview. Test, 10, 111-186.