Psicothema was founded in Asturias (northern Spain) in 1989, and is published jointly by the Psychology Faculty of the University of Oviedo and the Psychological Association of the Principality of Asturias (Colegio Oficial de Psicología del Principado de Asturias).
We currently publish four issues per year, which accounts for some 100 articles annually. We admit work from both the basic and applied research fields, and from all areas of Psychology, all manuscripts being anonymously reviewed prior to publication.
Psicothema, 1996. Vol. Vol. 8 (nº 1). 215-220
Julia Martínez-Cardeñoso, Marcelino Cuesta y José Muñiz
Universidad de Oviedo
Los modelos logísticos de Teoría de Respuesta a los Items más utilizados en la práctica asumen la unidimensionalidad de los datos, si bien esta asunción es muy difícil que ocurra estrictamente en situaciones reales. En el presente trabajo se investigó en qué medida influye la violación de la unidimensionalidad en el cálculo de un aspecto tan importante como es la función de información del test. Para ello se generaron datos simulados con distintos grados de dimensionalidad, estimando en cada caso los efectos sobre la función de información. En concreto se simularon 16 bloques de datos, originados al cruzar bases de dos y tres factores con 2 tipos de distribución y 4 tipos de correlaciones. En todos los casos se utilizaron 30 items y 1000 sujetos. Los resultados muestran que la función de información resulta razonablemente robusta a violaciones ligeras de la unidimensionalidad, resintiéndose progresivamente a medida que aumenta la dimensionalidad y las correlaciones entre los factores disminuyen.
Dimensionality and test information function. Logistic Item Response models assume data unidimensionality, although this assumption is difficult to obtain with empirical data. In this paper, the influence of unidimensionality violations on test information function was investigated. Sixteen data bases with different degrees of dimensionality were generated, by crossing the number of factors (2/3), with type of items distribution (uniform/no uniform), and factors correlations ( 4 levels). 30 items and 1000 subjects were used. Results show that the test information function appears to be robust to mild violations of unidimensionality, decreasing the robustness when the number of dimensions increases.
Los modelos de teoría de respuesta a los ítems (TRI) se han convertido en el enfoque predominante en el campo de la teoría de los tests, debido a que aportan soluciones novedosas a problemas no resueltos adecuademente en el marco de la teoría clásica. Los modelos logísticos más utilizados actualmente asumen que los datos son unidimensionales, aunque es bien sabido que en la práctica una unidimensionalidad absoluta es difícil de conseguir, dado que hay muchos factores no controlados que afectan a las respuestas de los sujetos (Ackerman, 1992; Osterlind, 1994 y Traub, 1983). Este hecho ha potenciado el estudio de la robustez de los modelos cuando se utilizan en situaciones de unidimensionalidad no perfecta (Cuesta y Muñiz, 1994, 1995; Drasgow y Parsons, 1983; Harrison, 1986; Reckase, 1979).
El objetivo del presente trabajo será estudiar los efectos que tiene sobre la estimación de la función de información del test la utilización de modelos logísticos en situaciones en las que no se da una unidimensionalidad estricta. Para ello se generaron datos simulados con distinto grado de dimensionalidad y se estudiaron sus efectos sobre la estimación de la función de información.
Método
Simulación de los datos
Se generaron 16 bloques de datos, resultantes de cruzar el número de factores de primer orden (dos y tres factores), con el tipo de distribución de los pesos factoriales (distribución uniforme y sesgada) y con los pesos de los factores de primer orden con el factor principal (cuatro niveles de correlación, que van desde el caso unidimensional puro al caso claramente multidimensional). Asimismo, se generó un bloque adicional en el que se establece la unidimensionalidad perfecta (un sólo factor). De cada uno de estos bloques se realizaron cinco replicaciones y se mantuvo constante el número de ítems (30) y el tamaño de la muestra (1000).
La distribución uniforme se obtuvo asignando a cada factor el mismo número de ítems; en la distribución sesgada uno de los factores tiene mayor número de ítems que el resto: en el caso de dos factores el primero consta de 20 ítems y el segundo de 10, en el caso de tres cada factor tiene respectivamente 14, 8 y 8 items.
La simulación de datos se llevó a cabo a partir del modelo factorial jerárquico de Schmid y Leiman (1957) adaptado por Drasgow y Parsons (1983), mediante un programa en lenguaje FORTRAN realizado por A. Rojas Benito y M. Cuesta (Cuesta, 1993).
El modelo del factor común puede ser escrito en términos matriciales como sigue:
x = Ay + Be
donde
x: es un vector que contiene las n variables observables.
A: es una matriz de orden nxk de pesos en los k factores comunes.
y: es un vector que contiene los k factores comunes.
B: es una matriz diagonal (nxn) con los pesos en los factores únicos en la diagonal.
e: es un vector que contiene los n factores únicos.
Se asume que los factores únicos no están correlacionados entre sí ni con los factores comunes. Todos los términos están escalados con media cero y varianza unidad. Para el caso concreto de nuestra simulación es necesario, además, asumir que existe un factor de segundo orden que da cuenta de las correlaciones entre los factores comunes de primer orden cuando estos son rotados a una estructura oblícua. Schmid y Leiman (1957) recogen esta circunstancia donde los factores comunes vienen dados por:
Y= fZ+DV
donde:
f: es un vector de K elementos que contiene los pesos de los factores de primer orden en el factor general de segundo orden
Z: Vector que contiene las puntuaciones del factor de segundo orden
D: Es una matriz diagonal de orden KxK que contiene los pesos de los factores comunes de primer orden en los k factores de grupo de segundo orden
V: Vector con los k factores de grupo
Introduciendo esta expresión en el modelo general se pueden obtener los valores de x.
La dicotomización de las variables x se llevó a cabo utilizando como valores de los puntos de corte los mismos que los utilizados por Drasgow y Parsons (1983) en los primeros treinta ítems de su trabajo, ver tabla 2.
Analisis de los datos
Para determinar la influencia de la violación de la unidimensionalidad en la estimación de la función de información, se analizaron a) las discrepancias existentes entre los valores teóricos del punto donde la función de información aporta la máxima información y los correspondientes valores empíricos obtenidos, y b) las diferencias entre la cantidad de información máxima teórica y la obtenida empíricamente. Para los cálculos empíricos se utilizó el modelo logístico de dos parámetros implementado en la versión 1.1 del programa PC- BILOG.
El estadístico que se utilizó para el cálculo de las diferencias entre los valores teóricos y los valores estimados, siguiendo a Drasgow y Parsons (1983), fué el de las raíces de las diferencias cuadráticas medias (RDCM), cuya fórmula viene dada por:
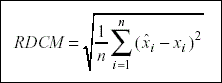
Teniendo en cuenta que se denomina test a aquellos análisis en los que se consideran los treinta items conjuntamente, y subtest a los subconjuntos de items que conformar un factor, se llevaron a cabo los siguientes análisis:
a) Cálculo de las raíces de las diferencias cuadráticas medias en los tests y en los subtests, entre el Punto de Información Máxima (PIM) y el parámetro b (dificultad) teórico, por ser éste el punto al que corresponde la información máxima (IM).
b) Cálculo de las raíces de las diferencias cuadráticas medias de la información máxima para los tests y los subtests.
c) Diferencia cuadrática media de la información máxima entre el test total y sus correspondientes subtests para cada uno de los bloques de datos simulados.
Resultados y conclusiones
Los valores correspondientes a las raíces de las diferencias cuadráticas medias entre el PIM estimado y PIM teórico o índice de dificultad son, como se indica en las tablas 3 y 4 mayores conforme las bases son más multidimensionales y sesgadas. También se puede apreciar una distancia mayor entre el punto de información máxima estimada y el índice de dificultad en los subtests que en el test total.
Las raíces de las diferencias cuadráticas medias entre la información máxima del test total estimado y la información máxima del test total calculada teóricamente son mayores en bases más multidimensionales y distribuciones sesgadas, y se obtiene un comportamiento semejante tanto en bases de dos factores como de tres (Tablas 5, 6).
La comparación entre la IM estimada del test total con la IM teórica de cada uno de los subtests no presenta un patrón claro en cuanto a si crece o decrece con la multidimensionalidad, sí presenta valores mayores en las RDCM de las distribuciones sesgadas.
Si se compara la información máxima de los subtests estimada y teórica se observa que disminuye el valor de las raíces de las diferencias cuadráticas medias en las bases más multidimensionales tanto con dos, como con tres factores y en distribuciones uniformes y sesgadas.
Como era de esperar, la función de información se ve afectada por la violación de la unidimensionalidad: tanto el punto de información máxima como la información máxima presentan estimaciones menos precisas a medida que aumenta la multidimensionalidad. Desde el punto de vista aplicado, cabría subrayar la necesidad de comprobar adecuadamente la dimensionalidad antes de utilizar la función de información como instrumento de análisis de los tests.
Ackerman,T. A.(1992). A didactic explanation of item bias, item impact, and item validity from a multidimensional perspective. Journal of Educational Measurement, 29(1), 67- 91.
Cuesta, M.(1993). Utilización de modelos logísticos unidimensionales con datos multidimensionales. Oviedo, Tesis Doctoral.
Cuesta, M. y Muñiz, J. (1994). Utilización de modelos unidimensionales de teoría de respuesta a los ítems con datos multidimensionales. Psicothema, 6(2), 283-296.
Cuesta, M. y Muñiz, J. (1995). Efectos de la multidimensionalidad en la estimación de parámetros desde modelos unidimensionales de Teoría de Respuesta a los Items. Psicológica, 16, 65-86.
Drasgow, F. y Parsons, C. K. (1983). Application of unidimensional item response theory models to multidimensional data. Applied Psychological Measurement, 7(2), 189-199.
Harrison, D. A. (1986). Robustness of IRT parameter estimation to violations of unidimensionality assumption. Journal of Educational Statistics, 11(2), 91-115.
Muñiz, J. y Hambleton, R. (1992). Medio siglo de teoría de respuesta a los ítems. Anuario de Psicología, 52, 41-66.
Osterlind, S. J. (1994). Constructing Test Item. Boston: Kluwer Academic Publishers.
Reckase, M. (1979). Unifactor latent trait models applied to multifactor tests: Results and implications. Journal of Educational Statistics, 4(3), 207-230.
Schmid, J. y Leiman, J.M. (1957). The development of hierarchical factor solutions. Psychometrika, 22(1), 53-61.
Traub, R. E. (1983). A priori considerations in choosing an item response model. En R. K. Hambleton (Ed.), Applications of item response theory. Vancouver Educational Research Institute of British Columbia.