Psicothema, 1999. Vol. Vol. 11 (nº 1). 175-182

Marcelino Cuesta y José Muñiz

Universidad de Oviedo

The effects of violating the unidimensionality assumption when applying item response logistic models were studied. Using a multidimensional two parameter logistic model, two different tests that are common in practice were simulated: a) a test composed of two equally relevant dimensions, and b) a test with a dominant dimension and a secundary one. Each test was composed of 40 items, 25 corresponding to the first dimension, 15 to the second. Two sample sizes (N= 300 and N= 1000) and five levels of correlation between the dimensions (0.05, 0.30, 0.60, 0.90, 0.95) were used to generate the data. The unidimensional two-parameter logistic model was used to estimate the item parameters and the ability of the examinees. The results indicate that the unidimensional estimates are consistently robust. Estimates of the item difficulty parameter are less affected by the violation of the unidimensionality assumption than the other item parameter estimates. The item discrimination parameter and the ability estimates are influenced by the size of the correlation between the dimensions and by the type of multidimensionality displayed by the data.

Robustez de los modelos logísticos de respuesta a los ítems a las violaciones del supuesto de unidimensionalidad. Se estudiaron los efectos de violar la asunción de unidimensionalidad cuando se aplican modelos logísticos de teoría de respuesta a los items. Usando un modelo logístico multidimensional de dos parámetros, se simularon dos tipos distintos de tests de uso común: a) un test compuesto de dos dimensiones igualmente relevantes y b) un test con una dimensión dominante y otra secundaria. Cada test se componía de 40 items, 25 de los cuales correspondían a la primera dimensión y 15 a la segunda. En la generación de los datos se emplearon dos tamaños de muestra (N=300 y N=1000) y cinco niveles de correlación entre dimensiones (0.05, 0.3, 0.6, 0.9 y 0.95). El modelo logístico unidimensional de dos parámetros fue usado para estimar los parámetros de los times y la habilidad de los sujetos. Los resultados indican que las estimaciones unidimensionales son consistentemente robustas. Las estimaciones del parámetro de dificultad se ven menos afectadas por la violación del supuesto de unidimensionalidad que el resto de los parámetros estimados. El parámetro de discriminación de los items y la habilidad estimada se ven influenciados por el tamaño de la correlación entre dimensiones y por el tipo de multidimensionalidad mostrado por los datos.

The most widely used item response theory models (the one-, two- and three-parameter logistic models) require that the data be unidimensional. With the growing utilization of these models to evaluate psychological and educational variables, some questions about their proper use have arisen. One of the most important issues to arise has been that of the nonfulfillment of the unidimensionality assumption by most of the real data analyzed with these models. Different authors have pointed out the difficulty of finding psychological and educational variables which strictly meet the condition of unidimensionality (Harrison, 1986; Hulin, Drasgow & Parsons, 1983; Reckase, 1979, 1985, 1989; Reckase & McKinley, 1982).

In addition to the nature of the construct being measured by a test, other collateral aspects can influence dimensionality. Birenbaum and Tatsuoka (1982) pointed out the effect of instruction on test dimensionality, and Traub (1983) states some questions which can affect the dimensionality of the test, such as instructions, the speed conditions, or the tendency of examinees to guess. Rosenbaum (1988) also poses the possibility of the presence of item bundles which share some information in common and could violate the assumption of unidimensionality. This preoccupation about the dimensionality of the real test data gave rise to a line of investigation centered on the robustness of item response theory (IRT) models to the violation of the unidimensionality assumption. Reckase (1979) found that when the dimensions of a test were equally important, the ability estimates obtained using a unidimensional model represented the average of the dimensions. Whereas, when the test was composed of a dominant dimension and a secondary one (Stout, 1987), unidimensional estimates of ability tend to capture the first factor. Within this framework, Drasgow and Parsons (1983) suggested avoiding the use of unidimensional models when the correlation between dimensions is below 0.40. Harrison (1986) and Cuesta and Muñiz (1994, 1995) reported similar results. Using two-dimensional data, Ansley and Forsyth (1985) found that the unidimensional estimates of discrimination and ability parameters tend to approximate the average of both dimensions, whereas the unidimensional estimates of the difficulty parameter seem to overestimate the parameters of the first dimension. Way, Ansley, and Forsyth (1988) did not find relevant differences when using compensatory and non-compensatory models. Results converging in the same direction are reported by other authors too (Ackerman, 1989; Doody-Bogan & Yen, 1983; McKinley & Reckase, 1983; Reckase, 1985; Yen, 1984).

In general terms, most of these studies show that IRT logistic models appear to be robust to moderate violations of the unidimensionality assumption. However, many situations common to everyday testing practice, in which the assumption of data unidimensionality is not likely to be strictly fulfilled, remain to be investigated. The central aim of this paper is to investigate the behavior of item and ability parameter estimates obtained with a unidimensional two-parameter logistic model when the data are bidimensional.

Two common situations in testing practice were investigated: Case 1, a test with two dimensions which are equally dominant, and Case 2, a test with one dominant dimension and one secondary one. These are two situations many practitioners face every day when evaluating psychological and educational traits. The correlations between the two dimensions were also taken into account.

Method

Data Simulation

The model used to simulate the data (McKinley & Reckase, 1983) is a multidimensional extension of the two-parameter logistic model. According to this compensatory model, the probability of a correct response to an item is:

P (x_ij = 1 /a_i, d_i, θ_j )= [e^{(a’_iθ_j+ d_i )} ] / [ 1+ e ^{(a’ _iθ_j+ d_i )} ] (1)

where:

P( x_ij = 1/a_i, d_i , θ _j ) is the probability of a correct response to item i by examinee j,

a_i is a discrimination parameter vector, d_i is a parameter related to the difficulty of the item, and

θ_j , is an ability parameter vector.

The exponent of the previous expression can be rewritten as

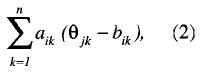
where:

n the number of dimensions,

a_ik an element of a_i,

θ _jk an element of θ _j , and

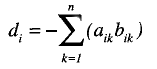
Based on the McKinley and Reckase (1983) model, Reckase (1985) proposed a new approach to the concept of difficulty, represented by d_i in the former model. Reckase introduces the multidimensional item difficulty (MID), which correspond to the point of the item response surface (IRS) where the ítem has the highest discriminatory power, that is to say where the item information is a maximum. In the unidimensional case, this value is given by the point of greatest slope of the item characteristic curve. However, when more than one dimension is involved, to define the difficulty parameter, the slope of a given point depends on the direction under consideration. That is why Reckase uses the distance from the origin of the latent space to the point of maximum discrimination, as well as the direction of this point with respect to the axes representing the dimensions under consideration. The distance from the origin is calculated according to the following expression:

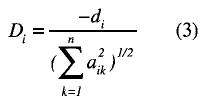
and the direction:

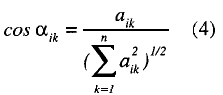
In accordance with this redefinition of the difficulty, for two items to be comparable it is necessary that they measure the same combination of abilities, that is to say, that they have the same direction.

Using MID as a starting point, Reckase (1986) proposed a related multidimensional discrimination index (MDISC). The definition put forward by the MDISC is presented as a function of the slope of the IRS at the point of greatest slope, in the direction indicated by the MID. The value of this parameter is:

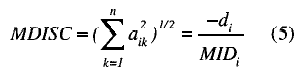
The generation of data according to this multidimensional model was performed with the M2GEN2 program developed by Ackerman (1989). The program allows the generation of two-dimensional data with different levels of correlation. As input, this generator requires a discrimination parameter vector for each of the dimensions, and a vector of item difficulties. As output, the program offers the examinees ability for each of the two dimensions, and the matrix (examinees x items) of ones and zeros from which the values were estimated.

Data Sets

Five levels of correlation between the generated dimensions were used: 0.05, 0.30 , 0.60, 0.90, 0.95. Two sample sizes were used: N=300 and N=1000. The two generated dimensions, θ₁ and θ₂, were scaled with a mean of zero and variance of one, N(0,1).

To simulate the ability parameters (Case 1), the Reckase (1985, 1986) data were used: 25 highly discriminating items on one of the dimensions, and 15 on the other (Table 1). The same values were used for Case 2, but the highest discrimination indices always appeared on the first dimension.

Data Analysis

Coefficient alpha (Cronbach, 1951), factor analysis, and other descriptive statistics were performed using the SPSS/PC statistical package. Logistic item response models parameter estimates were obtained via BILOG (Mislevy & Bock, 1984). The root mean squared differences (RMSD) and Pearson's correlations were used to compare the multidimensional parameters with the correspondent unidimensional estimates.

Results

Case 1

Table 2 shows the descriptive statistics for the data for case 1. The correlations between the ability simulated data [r( θ₁,θ₂)] are very Glose to the levels of correlation intended. The coefficient alpha appears to be high under all conditions, ranging from 0.90 to 0.95. The first three eigenvalues obtained from a principal component analysis are reported as an approxima tion to the dimensionality of each set of test data. The explained variance increases with the correlation between the dimensions. The mean and standard deviation are also reported. The sample sizes used (N= 300, and N= 1,000) did not seem to play an important role in the accuracy of the estimates, that is why in the tables only the results corresponding to N= 1,000 are reported.

Table 3 shows the accuracy of unidimensional model parameter estimates obtained from two-dimensional data. As the correlation between dimensions increases, the precision of the estimates improves. The discrimination for an item parameter on the second dimension (a₂) is always closer to the unidimensional estimate (a^') than the discrimination parameter for the item on the first dimension (a¹). However, the mean of both item discrimination parameters (a_m) is closest to the unidimensional estimate. The greatest distance appears with respect to the multidimensional discrimination index (_md).

The parameters a₁ and a₂ follow inverse patterns in their correlation with the unidimensional estimates. When the correlations between the dimensions are cower, the unidimensional estimates are more correlated with the ítem discrimination parameter of the first dimension. As the correlation between both dimensions increases, the correlation of the unidimensional estimates with the second dimension increases, decreasing with the first.

Very high correlations were found between the unidimensional difficulty parameter estimates and parameters d and D.

The accuracy of the unidimensional ability estimates increased with the increasing of correlation between dimensions (Table 4). These estimates are very Glose to the mean of the ability parameters of both dimensions (θ_m ), with correlations ranging from 0.93, when dimensions are uncorrelated, to 0.97, when the dimensions correlate 0.98.

Case 2

In this second case, as previously pointed out, a test with a principal dimension and a secondary one was simulated. The descriptive statistics of the data used appear in Table 5.

As in case 1, the values of coefficient alpha are very high for all data bases. The size of the first eigenvalue, and the similarity of the second and the third, indicates in all cases factorial unidimensionality. It seems, therefore, that from a factorial point of view this test is clearly unidimensional.

The estimation of the discrimination parameter (see Table 6) is closer to the mean of the parameters of the dimensions than to any of the other indicators considered. The multidimensional discrimination index also has high correlations with the unidimensional estimates.

The correlations between the b estimates and the parameters d and D presented in Table 7 were very high (l 0.92 to 0.99 l). As regards the estimation of the ability (Table 7) of the subjects, the predominance of the first dimension over the second is clear. As the correlation between the two dimensions increases, the relation between the unidimensional estimation and the second dimension also increases. Correlations between the unidimensional estimates and the ability average of both dimensions are very high, with values ranging from 0.88 to 0.97.

Conclusions

The main goal of this research was to investigate the degree to which the violation of the uidimensionality assumption affects the applicability of the most popular item response logistic models. Of the three unidimensional model parameters which have been considered (a, b, and q), the difficulty (b) seems to be the least affected by the violation of the unidimensionality assumption. This result is in accordance with that found in similar works by Ackerman (1989, 1991) and Oshima and Miller (1990). The parameter d, as well as the distance to the point of maximum discrimination, are seen to be highly related to the unidimensional item difficulty estimates, exhibiting no important differences between the results obtained in case 1 and case 2. The unidimensional estimates of the discrimination parameter a seem to capture the average values of the parameters assigned to each of the two dimensions when there exists a certain correlation between the dimensions (r≥ 0.3). The correlations between the unidimensional estimates and MDISC are also high; especially when the dimensions are strongly correlated. The correlations between MDISC and the unidimensional estimates (case 2) always have higher values than those found in case 1. Some differences are observed between the estimates of the item discrimination parameter. While in the first case, a₁initially captures the attention of the unidimensional estimates, that attention gradually changing to a₂ in the second case, a relatively high correlation with a₁ is always present, converging also a₂ to this correlation when the relation between θ₁ , and θ ₂ increases. In the tests with uncorrelated dimensions, it was found that the relation between a₁ and a₂ with the unidimensional estimates is very close. The sample sizes used (N=300 and N=1.000) do not seem to affect the accuracy of estimates. The robustness of the model parameter estimates is especially strong when the correlation between the two dimensions of the simulated test is above 0.30; increasing the precision with increasing correlation between the dimensions. The unidimensional estimates of bidimensional tests tend to capture the average of the parameters of the test dimensions.

Confirming most of the previous research (Ackerman, 1989; Ansley & Forsyth, 1985; Drasgow & Parsons, 1983; Harrison, 1986; Way, Ansley & Forsyth, 1988; Yen, 1984), the general conclusion of this study is that the unidimensional estimates of item parameters (difficulty and discrimination) and examinee ability were consistently robust to moderate violations of test unidimensionality. At an applied level, these results seem to indicate that when the test has a dominant dimension, even when the dimensions measured by the test are uncorrelated, the violation of the assumption of unidimensionality does not produce serious errors in model parameter estimation, especially with respect to ability estimation.

Ackerman, T. A. (1989). Unidimensional IRT calibration of compensatory and noncompensatory multidimensional items. Applied Psychological Measurement, 13(2), 113-127.

Ackerman, T. A. (1991). The use of unidimensional parameter estimates of multidimensional items in adaptative testing. Applied Psychological Measurement, 15(1), 13-24.

Ansley, T. N., & Forsyth, R. A. (1985). An examination of the characteristics of unidimensional IRT parameter estimates derived from two-dimensional data. Applied Psychological Measurement, 9(1) 37-48.

Birenbaum, M., & Tatsuoka, K. K. (1982). On the dimensionality of achievement test data. Journal of Educational Measurement, 19(4), 259-266.

Cronbach, L. J. (1951). Coefficient alpha and the internal structure of tests. Psychometrika, 16, 297-334.

Cuesta, M., & Muñiz, J. (1994). Utilización de modelos unidimensionales de teoría de respuesta a los items con datos multifactoriales. Psicothema, 6(2), 283-296.

Cuesta, M., & Muñiz, J. (1995). Efectos de la multidimensionalidad en la estimación de parametros desde modelos unidimensionales de teoría de respuesta a los items. Psicológica, 16, 65-86.

Doody-Bogan, E. N., & Yen, W. M. (1983, April). Detecting multidimensionality and examining the effects of vertical equating with the three-parameter logistic model. Paper presented at the meeting of the American Educational Research Association, Montreal.

Drasgow, F., & Parsons, C. K. (1983). Application of unidimensional item response theory model to multidimensional data. Applied Psychological Measurement, 7(2), 189-199.

Harrison, D. A. (1986). Robustness of IRT parameter estimation to violations of unidimensionality assumption. Journal of Educational Statistics, 11(2), 91-115.

Hulin, C. L., Drasgow, F., & Parsons, C. K. (1983). Item response theory Applications to psychological measurement. Homewood, IL: Dow Jones-Irvin.

McKinley, R. L., & Reckase, M. D. (1983). An extension of the two parameter logistic model to the multidimensional latent space (Research Report No. 83-2). Iowa City, IA: The American College Testing Program.

Mislevy, R. J., & Bock, R. D. (1984). BILOG: Maximun likelihood item analysis and test scoring with logistic models. Mooresville, IN: Scientific Software.

Oshima, T. C., & Miller, M. D. (1990). Multidimensionality and IRT based item invariance indexes: The effect of between-group variation in trait correlation. Journal of Educational Measurement, 27, 273-283.

Reckase, M. D. (1979). Unifactor latent trait models applied to multifactor tests: results and implications. Journal of Educational Statistics, 4(3), 207-230.

Reckase, M. D. (1985). The difficulty of test items that measure more than one ability. Applied Psychological Measurement, 9(4), 401-412.

Reckase, M. D. (1986, April). The discriminating power of items that measure more than one dimension. Paper presented at the meeting of the American Educational Research Association, San Francisco.

Reckase, M. D. (1989, August). Controlling the psychometric snake: or, how I learned to love multidimensionality. Invited address at the meeting of the American Psychological Association, New Orleans.

Reckase, M. D., & McKinley, R. L. (1982). The feasibility of a multidimensional latent trait model. Paper presented at the meeting of the American Psychological Association, Washington.

Stout, W. (1987). A nonparametric approach for assessing latent trait unidimensionality. Psychometrika, 52(4), 589-617.

Rosenbaum, P. R. (1988). Items bundles. Psychometrika, 53, 349-359.

Traub, R. E. (1983). A priori considerations in choosing an item response model. In R. K. Hambleton (Ed.), Applications of item response theory. (pp. 57-70). British Columbia: Educational Research Institute of British Columbia.

Way, W. D., Ansley, T. N., & Forsyth, R. A. (1988). The comparative effects of compensatory and noncompensatory two-dimensional data on unidimensional IRT estimates. Applied Psychological Measurement, 12(3), 239-259.

Yen, W. M. (1984). Effects of local dependence on the fit and equating performance of the three parameter logistic model. Applied Psychological Measurement, 8(2), 125-145.