LA MODELIZACIÓN DE RELACIONES NO LINEALES: ASPECTOS TEÓRICOS

Pilar Jara Jiménez, Jaume Arnau i Gras^*, Jesús Rosel y Antonio Caballer Miedes

Universidad Jaume I y ^* Universidad Autónoma de Barcelona

En muchas ocasiones las relaciones entre la/s variable/s respuesta/s y las predictoras pueden considerarse en el marco de la linealidad asumiendo como válida la ecuación de la recta desde la que se obtendrán los estimadores adecuados. No obstante, existen situaciones en las que no puede mantenerse la referencia a la linealidad en las relaciones entre variables. Por tanto, es preciso acudir a otras funciones que representen de forma más adecuada las anteriores relaciones. La estrategia de modelización, en el marco de la regresión no lineal, permite realizar una elaboración interactiva de procedimientos de identificación, estimación, validación y uso de los modelos. Desde esta perspectiva, es posible abarcar una gran cantidad de posibilidades de acuerdo con diferentes características desde las que considerar las variables implicadas. Así, podría repararse, entre otros, en modelos con variable independiente fija, modelos con variable independiente aleatoria, modelos con variables cualitativas o modelos con errores autocorrelacionados. La exposición del trabajo que se presenta trata de dar a conocer algunos aspectos teóricos que deberían considerarse a la hora de obtener modelos representativos de relaciones no lineales entre variables.

Modelling non-linear relationships: theoretical aspects. In many cases, the relationship between dependent and independent variables can be considered to be linear, assuming that the equation of the line from which the estimators are obtained is valid. However, there are situations in which the linearity cannot be maintained in the relationships between the variables. Thus, other non-linear functions must be used to represent them. The non-linear strategy of modelling allows us to perform, in an interactive way, the identification, estimation and validation procedures as well as the application of the models. From this point of view, it is possible to cover a large number of possibilities in function of the different characteristics of the variables involved. In this way, different models, such as those involving fixed independent variables, random independent variables, qualitative variables or autocorrelated errors can be used. This paper presents some theoretical aspects which should be taken into account during the process of fitting non-linear models, whose aim is to obtain valid relationships between variables.

Algunas de las razones por las que no se admite un modelo de regresión lineal como representativo de la relación entre dos (o más) variables, pueden ser la falta de significación de los parámetros implicados o que dicha relación lineal resulte pobre debido a un bajo indicador en el coeficiente de determinación. En cualquiera de estos casos, cabe apuntar posibilidades: en primer lugar, que no existe relación entre las variables; en segundo lugar, que existiendo relación entre ellas ésta no puede considerarse desde el modelo lineal; en tercer lugar, aunque el modelo lineal funcione bien podríamos considerar un modelo no-lineal por el que obtener una interpretación completa de los parámetros (Seber y Wild; 1989, Pág 5).

La consideración de las relaciones entre variables desde un planteamiento no-lineal como modelo explicativo da lugar a que las posibilidades de obtener una función mediante la que representar la relación se amplíen enormemente. No obstante, antes de abordar esta posibilidad, conviene matizar a qué nos estamos refiriendo cuando consideramos la no-linealidad en una ecuación de regresión. En este sentido, estableceremos, con cuatro modelos, la evolución desde la regresión lineal a la no-lineal (en el sentido más estricto):

En primer lugar, la regresión lineal, en su concepción más simple, podría expresarse según la ecuación:

En segundo lugar, en la evolución hacia la no-linealidad, podemos considerar la ecuación:

En esta ecuación, se representa la relación «no-lineal» entre la variable dependiente (Y) y la variable independiente (X), en la que la consideración cuadrática en ésta determina observaciones simples en aquélla. Estos modelos pueden considerarse no-lineales en las variables (Neter, Wasserman y Kutner, 1989; Seber y Wild, 1989; Ratkowsky, 1990); si bien, continúan siendo lineales en los parámetros que marcan el grado de ajuste entre ambas. La transformación de la ecuación (2), mediante el cálculo de la raíz cuadrada de la variable, conduciría hacia la evitación del término cuadrático y, por tanto, podría considerarse como un modelo de regresión lineal.

En tercer lugar, otra forma de considerar en la representación de la ecuación de regresión podría ser mediante la ecuación:

La ecuación (4), representa a un modelo no-lineal en los parámetros ß_o y ß₁. Sin embargo, como apuntan Neter, Wasserman y Kutner (1989), este modelo debe considerarse como intrínsecamente lineal, debido a que, mediante la aplicación de logaritmos, podría expresarse linealmente, como se especifica en:

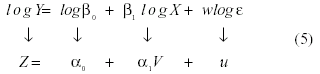
Así, la ecuación (4), no lineal en los parámetros se ha transformado, en (5), en un modelo lineal. Sin embargo, conviene tener presente que debería hacerse una valoración del nuevo modelo obtenido, puesto que, por ejemplo, cabe la posibilidad que el componente de error no siga la distribución normal que tenía en el modelo original. En estos casos, es preciso observar si se mantiene el cero como valor esperado y si la varianza es constante o precisa alguna transformación que estabilice dicha varianza en el error.

En cuarto lugar, podemos considerar un modelo de regresión no-lineal en los parámetros, e intrínsecamente no-lineal, como se representa en:

En esta ecuación la no-linealidad se produce en los parámetros, dado que al menos una de las derivadas de Y con respecto a los parámetros ß_o y ß₁, es función de, al menos, uno de los parámetros. Así, la derivada de Y respecto de ß_o, y la derivada de Y respecto de ß₁, son función de ß_o y/o de ß₁. Además, no existe posibilidad de linealizar la ecuación.

La obtención de Modelos de Regresión no-Lineal

Si tuviésemos que resumir la estrategia analítica plantearíamos un esquema interactivo entre las facetas de identificación, estimación y validación.

(1) IDENTIFICACIÓN (ver Figura 1). La estrategia de modelización debería comenzar por tratar de dar respuesta a la siguiente pregunta: ¿Existe algún modelo teórico y/o evidencia empírica suficiente en los que basarnos para seleccionar la función no-lineal apropiada? Si la respuesta no es afirmativa convendría considerar, al menos, dos aspectos:

a) Las características de las variables que se están considerando. Es decir, ¿Cómo se han obtenido los valores de la variable independiente?

b) El aspecto de la representación gráfica de los datos:

(2) ESTIMACIÓN. Se expone un esquema de la estimación de parámetros en la Figura 2.

La estimación de los parámetros en una ecuación de regresión lineal produce estimadores insesgados, normalmente distribuidos, eficientes y consistentes, que son las propiedades deseables para cualquier estimador. No obstante, aunque existen muchas diferencias, entre los modelos no-lineales estas propiedades se obtienen sólo de forma asintótica. En los apartados que siguen trataremos de exponer algunas posibilidades para obtener buenos estimadores en las ecuaciones de regresión no-lineal.

(2.1) MÍNIMOS CUADRADOS NO-LINEALES.

Desde los planteamientos lineales, el procedimiento de estimación de parámetros, considerando mínimos cuadrados, consiste en obtener los valores que reducen al máximo el componente de error, teniendo en cuenta que:

Dos posibles formas de obtener tales valores podrían ser mediante sucesivas combinaciones de valores hasta conseguir que el sumatorio fuese mínimo, es decir, mediante búsquedas numéricas o, extrayendo las ecuaciones normales obtenidas de la diferenciación respecto de los parámetros e igualando a cero. Ambas posibilidades podrían también observarse en el caso de la regresión no-lineal (Neter, Wasserman, Kutner, 1989).

Solución por Ecuaciones Normales

Dada una relación funcional conocida como Y_i= ƒ(X_i; θ)+ε, donde ƒ(X_i; θ) fuese, p.e., ß₀e^ß1X, el criterio C de mínimos cuadrados podría expresarse del siguiente modo:

Donde la derivada parcial de C respecto del parámetro j sería:

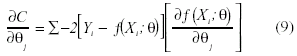
Por tanto, para ß₀e^ß1X, las ecuaciones normales se obtendrían según:

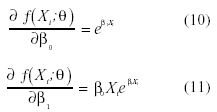
Sustituyendo ß₀ y ß₁ por b₀ y b₁ en (10) y (11), las ecuaciones serían:

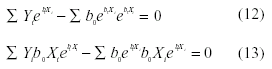
Que simplificadas serían:

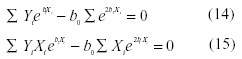
Estas ecuaciones normales, como en muchos modelos no-lineales, no tienen una solución analítica, por lo que es preciso el recurso de algún procedimiento iterativo que permita encontrar una solución.

Solución por Búsqueda Numérica: procedimiento de Gauss-Newton

En la mayoría de los programas informáticos estadísticos se emplean una o varias estrategias de búsqueda numérica directa que dan solución a los problemas de la regresión no-lineal. Entre ellas, el Método de Linearización o de Gauss-Newton (GN) (Bard, 1974; Kennedy y Gentle, 1980; Draper y Smith, 1981; Bates y Watts, 1988; Neter, Wasserman y Kutner, 1989) está basado en una modificación hecha por Gauss (1809) al algoritmo de Newton que resulta más eficiente que el procedimiento de Newton (Seber y Wild, 1989, pág 621), debido a la rápida convergencia, en la mayoría de los casos, desde unos valores tomados inicialmente, hacia los modelos próximos a la linealidad.

El procedimiento de GN utiliza las expansiones de las series de Taylor para aproximar el modelo de regresión no-lineal hacia términos lineales y emplea la estrategia de mínimos cuadrados ordinarios para estimar los parámetros. La iteración de estos pasos lleva, generalmente, hacia soluciones planteadas por los problemas de la regresión no-lineal.

La forma de proceder supone al inicio, considerar una serie de valores para los parámetros de regresión ß₀, ß₁,..., ß_p-1 a los que podríamos nombrar como: b⁽⁰⁾ ₀ , b⁽⁰⁾ ₁ ,..., b⁽⁰⁾_p-1 (el supraíndice especifica el número de iteraciones). Algunas de las posibilidades para obtener estos valores pueden basarse en estudios previos, expectativas teóricas o búsquedas previas para los parámetros que conducen a bajos valores del criterio C (ver ecuación 8).

La expansión de las series de Taylor para n casos, considerando los valores iniciales b⁽⁰⁾_K podría representarse para el caso «i» del siguiente modo:

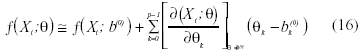
Donde el vector de parámetros de valores iniciales sería:

Para representar de una forma más esquemática la ecuación (16), podríamos considerar las siguientes posibilidades:

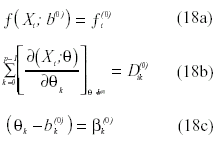
Sustituyendo en (16), las ecuaciones de la (18a) a la (18c), podríamos re-escribir la serie de Taylor del siguiente modo:

Y dado que Y= ƒ(X_i;θ)+ε_i, podríamos expresar el modelo completo:

Donde apreciaríamos que si Y_i⁽⁰⁾= Y_i - ƒ_i⁽⁰⁾, la ecuación (19) quedaría:

Cuya forma matricial sería:

El modelo representado en (21) tiene la estructura del modelo lineal de regresión, del que se diferencia en que la matriz de éste se ha sustituido por la matriz de derivadas parciales. Por tanto, podríamos estimar los valores de ß⁽⁰⁾ considerando las ecuaciones normales del procedimiento de regresión lineal ordinario:

Desde (22) obtenemos el vector de estimadores que podemos utilizar para obtener coeficientes revisados como se muestra a continuación:

Así, b⁽¹⁾ _k es vector de un estimadores de θ_k tras la primera iteración. Para comprobar si los ajustes se están realizando apropiadamente podemos acudir al criterio mínimo cuadrático C; para ello, tomamos el vector de estimadores iniciales b⁽⁰⁾ y obtenemos la suma cuadrática residual (SSE), para dichos valores iniciales, tal como se muestra a continuación:

Después, consideramos el vector de estimadores obtenido tras la primera iteración y, similarmente a (24), obtenemos la según la igualdad:

Si SSE⁽¹⁾ < SSE⁽⁰⁾ podríamos concluir que los coeficientes revisados son mejores que los iniciales. Por tanto, el algoritmo de GN estaría trabajando convenientemente.

El procedimiento descrito se repite, tomando ahora como valores iniciales los estimadores obtenidos en b⁽¹⁾, hasta que la diferencia entre estimaciones sucesivas y/o la diferencia entre las medidas de sus SSE son muy pequeñas.

En este punto, conviene destacar que la función ƒ(X_i; θ) se utiliza en las aproximaciones a las series de Taylor; pero, las funciones ƒ(X_i;b⁽⁰⁾) y ƒ(X_i;b⁽¹⁾) se consideran para la obtención de SSE⁽⁰⁾ y SSE⁽¹⁾, respectivamente.

(3) VALIDACIÓN. En lo referente al estudio de la aptitud de un modelo no-lineal puede realizarse de modo similar al lineal, pero considerando, en el caso no-lineal, el error típico aproximado (ASE) de cada parámetro, a la vez que n-p grados de libertad. De esta manera, se entiende que si H₀ : ß_j = q, vs.H1 : ß_j ≠ q, según el contraste , no se aceptará la H_o si

Diferentes representaciones gráficas de los residuales obtenidos: gráfico de cajas, gráficos P-P normal o gráfico Q-Q normal, así como la línea ajustada por el modelo, permiten observar las diferencias entre el modelo asumido y el comportamiento real de los datos. Si existe la sospecha de presencia de autocorrelación entre los residuales, puede recurrirse al test de Durbin-Watson , así como al estudio de las funciones de autocorrelación simple y parcial de los residuos.

(4) VALORACIÓN. Cuando existan distintos modelos que cubran adecuadamente los pasos que se han expuesto anteriormente deberá valorarse cuál es el seleccionado. Para ello, podemos acudir a aquel que explique la mayor cantidad de varianza con el menor número de parámetros.

(5) APLICACIÓN. Este tipo de modelos, como debería considerase en cualquier modelización, no deberían utilizarse sin un conocimiento de las implicaciones que conllevan; por tanto, no deberían ser simples sustitutos de modelización para aquellos casos en los que no parece adecuado el modelo lineal. Por ello, parece conveniente hacer algunas alusiones acerca de algunos de los modelos no-lineales más frecuentemente utilizados. Las aplicaciones de este tipo de modelos pueden considerarse para tratar de dar respuesta a cuestiones similares a las que se plantean en regresión lineal, desde el marco no-lineal. Una de las aplicaciones más notables en Psicología se plantea desde el uso de Modelos de Crecimiento en diferentes ámbitos de contenido: aprendizaje, ámbitos evolutivos, adquisición de destrezas, etc.

A modo de conclusión

En resumen, el modelo obtenido mediante regresión no lineal es un procedimiento de ajuste de datos adecuado para el supuesto de que las variables no sigan relaciones lineales. Posiblemente, la ausencia de aplicación de estos modelos a la Psicología, tal vez sea debida más al desconocimiento del método por parte de los psicólogos, que a la gran utilidad analítica de los mismos. Es de esperar que en un futuro próximo este tipo de modelos se utilice con más frecuencia.

Glasbey, C.A. (1980), Non-linear regression with autorregresive time series error. Biometrics, 36, 135-140.

Ratnowsky, D. A. (1980), Handbook of nonlinear regression models. New York: Marcel Dekker, Inc.

Seber, G.A.F. y Wild C.J. (1989). Ed: Wiley. Non-Lineal regression.