Psicothema, 2001. Vol. Vol. 13 (nº 2). 271-276

Rafael Rabadán, Manuel Ato and María F. Rodrigo

This study offers relatively new methodological tools for an accurate and exhaustive analysis of categorical data, such as those from nominal and ordinal scales usually reported by means of contingency tables. The data about change in dieting status for men and women collected by Heatherton et al. (1997) in their longitudinal study of eating behavior, are reanalyzed now through an alternative approach, consisting of several applications derived from Generalized Linear Models. These techniques can result highly useful for a desirable increase in the rate of repeated measures or panel works, whose data have been in most occasions missanalyzed so far because of an abusive rest on the classic statistical methods. A very interesting feature observed throughout this modeling approach is the different patterns of eating behavior by gender; so the same models must not be applied to the analysis of women’s and men’s responses, on pain of losing crucial information.

Comportamiento alimentario por sexos: un enfoque metodológico alternativo para el análisis de datos categóricos. En este artículo se proponen instrumentos metodológicos relativamente nuevos para analizar datos categóricos con precisión y exhaustividad, como los datos procedentes de escalas nominales y ordinales que usualmente se presentan en tablas de contingencia. Heatherton y otros (1997), en su estudio longitudinal sobre comportamiento alimentario, recogieron datos sobre cambio en hábitos de dieta que se reanalizan ahora desde un enfoque alternativo, compuesto de varias aplicaciones derivadas de los Modelos Lineales Generalizados. Estas técnicas pueden resultar muy útiles de cara al deseable incremento en el número de trabajos con medidas repetidas y diseños de panel, cuyos datos han sido en muchas ocasiones pobremente analizados debido sobre todo al abusivo recurso a los métodos estadísticos clásicos. Un rasgo muy interesante observado gracias a este enfoque de modelado es la existencia de diferentes patrones de conducta alimentaria según sexos, por lo que modelos idénticos no deberían aplicarse al análisis de las respuestas de hombres y de mujeres, so pena de perder información importante.

A very important part of present research about human behavior points to eating aspects as disorder symptoms, dieting, restraint, weight loss, body weight and image, body dissatisfaction, risk factors for chaotic eating behaviors such as anorexia or bulimia, and so on, focusing main results towards psychosocial influences and gender differences. Moreover, developmental stages as puberty, adolescence and early adulthood are being studied in detail, because of their higher risk of suffering such disorders. The vast majority of published research uses transversal samples, but only a few works are concerned with stability and change analysis of behavioral patterns from longitudinal samples, repeated measures designs or panel studies.

One of the main advances of data analysis in the last quarter of this century is due to the development and application of Generalized Linear Models (GLMs) introduced by Nelder and Wedderburn (1972), which establish a methodological framework that allow us a fine analysis of every kind of information, especially useful in categorical data analysis (CDA). So the efforts of authors such as Bishop, Fienberg and Holland (1975), Goodman (1978), McCullagh and Nelder (1989), Agresti (1990) or Hagenaars (1993), among other contributors, have opened smart perspectives for the improvement of CDA within the procedure known as statistical modeling.

The aim of this work is to analyze the change with categorical data to test alternative behavioral patterns. We can show the benefits derived from this new framework by using a real dataset and attempting to achieve a bigger exploitation than traditional analyses have done. For instance, by searching for a previous study to go deep inside the data to prove particular hypotheses with the tools provided by CDA.

The remainder of this paper is organized as follows. We first present a real dataset as an illustrative example of longitudinal, repeated measures work. Later we propose several models to analyze it deeply, from the classic independence model to more recent approaches such as marginal and simultaneous modeling. The last part is a discussion to summarize some previous ideas and to suggest future lines of research.

The Heatherton et al. (1997) data

In their longitudinal study of dieting and eating attitudes and disorders by gender, Heatherton, Mahamedi, Striepe, Field, and Keel (1997:121, Table 2) examine longitudinal (10-year) and group (women vs. men) changes in categorical (ordinal) variables, but only through the traditional χ² perspective.

Heatherton et al. (1997:118) propose that "the primary goal of the current study was to examine stability and change in a wide spectrum of eating behaviors over a reasonably long period", we take again their panel data in order to attempt several new hypotheses about relationship patterns among variables, beyond the simple independence hypothesis that these authors limit to testing with the same table.

Transforming to observed frequencies the percentages displayed in that article and adding up their total marginals for rows and columns, the 2x4x4 contingency table remains.

Summarizing these data, 502 women and 205 men had to select a specific category for their particular dieting status in two moments ten years apart. We have then repeated measures of ordinal responses at two time points (within-subjects variable) for both gender groups (between-subjects variable), a longitudinal dependent-samples or matched-pairs design. The authors indicate that participants (original N=715) had been college students at a selective northeastern college in 1982, comprising the global sample 509 women and 206 men ranging in age from 27 to 55 (M=30.0, SD=2.0) in 1992.

Fitting models

The main goal of this work being to offer some analyses by means of GLMs to take maximum advantage of categorical data as shown in the example, we could begin the session of statistical modeling with a simple, intuitive verification: How many people maintain their primitive dieting status 10 years later? That is, what amount of absolute stability yields this kind of eating behavior? Really the most important frequencies to judge this question are those in the main diagonals, so we can take such scores and add them: (71+24+64+26)/502=.369, a 37% of women remained at the same level, and (99+8+15+2)/205=.605, an approximate 61% of men stayed in the same category. The majority of men therefore were highly stable (stayers) in their attitude towards dieting, whereas most of women changed their original status (movers).

Focusing to complementary percentages as Heatherton et al. (1997) do, we find in the upper triangle 18% of women becoming more intense dieters from 1982 to 1992, while the lower matrix implies 45% of women - the relative majority for this gender - losing to some degree their interest in dieting. On the other hand 31% of men increased dieting between those years, whereas 8% decreased. So at a first glance in changes of attitudes, men gain more interest in dieting with time than women do. The authors suggest possible reasons for these changes.

For subsequent data analysis we shall use an experimental version of the LEM program (Vermunt, 1997).

Independence and Quasi-Independence models

In a series of sharper analyses for square contingency tables, the first test is usually the independence one. Taking the likelihood ratio L² or G² statistic (Wilks, 1935) instead of the X² statistic –an habitual choice in loglinear contexts mainly because of the Maximum Likelihood method generally applied to CDA– we obtain for women a deviance value D=82.18 with (I-1)(J-1)=9 degrees of freedom (df from now on), and for men D=55.77 with 9 df, p<.0001 in the two tests. The loglinear model of independence does not fit these data, so we can suppose some type of meaningful relationship between 1982 and 1992 responses for both genders. This paper from here onward attempts to settle the nature of that correlation.

The quasi-independence hypothesis (QI) could be the next one to test, because as Agresti (1990:355) argues "an effect of the dependence between matched pairs is that square tables usually have larger counts on the main diagonal than the independence model predicts; conditional on the event that a matched pair falls off the main diagonal, though, there may be a simple structure for the relationship." So, fitting an independence model but preserving the frequencies on the main diagonal (n_ij = m_ij for all i=j), 12 scores to be matched and examined inside each subtable; in symbolic notation, we contrast each n_ij vs. each n_ji for all i≠j (I being the number of rows and J the number of columns; of course I=J in square tables), a special case of the quasi-symmetry structure to be analyzed below (and certainly both hypotheses are equivalent when I≤3). The quasi-independence model for women yields D=22.45 with (I-1)² - I=5 df (p<.0001), but, in remarkable contrast, a reduced L² or deviance for men, D=4.59 with 5 df, with a high goodness-of-fit (p=.468). Following Agresti, this type of models are very useful in tables with a large amount of scores in the main diagonal, and that is precisely the case for men, with nearly 61% of frequencies in just those positions.

Employing a model comparison criterion (e.g. the BIC index by Raftery, 1986, 1995) as standard reference to compare the next well-fitted models,

BIC= D - df x log(n) = 4.59 - 5 x log(205)= - 22.03

A lower value stands for a better fit.

Narrowly related to the QI model is the parallel triangles model, introduced by Goodman (1972). Once the former one fits well, the modeller may wonder about a more complicated structure where, besides the particular parameters for the main diagonal, data within both triangle matrices are compared. This model fits very well for men’s data, giving D=4.09 based on 4 df, with p=.394 and BIC= - 17.20; so losing 1 df - just required to compare the triangles - we obtain a deviance 0.5 points lower. Anyway, the BIC value is better for the previous model.

Symmetry, Quasi-Symmetry, and Marginal models

We could go on testing differences between the cell frequencies in both sides out of the main diagonal. For such a purpose one of the best hypotheses is the symmetry model, which consists of the following stages: denoting by n_ij the observed frequency inside the ij cell in an IxJ square contingency table, and by m_ij its estimated frequency, the symmetry hypothesis - also known as full symmetry or axial symmetry - attempts to determine the degree to which a similar structure between the frequencies in symmetric positions can be assumed, i.e., the real level of similarity between those scores whose subindices are interchangeable (i.e., if n_ij≈n_ji). The estimated values under this hypothesis must then satisfy m_ij=m_ji for all i≠j, or external values with regard to the main diagonal. The usual way to check this type of similarity consists in finding the mean for the symmetric cells, m_ij = m_ji =(n_ij + n_ji)/2, and then testing the statistical significance for the differences between each observed n_ij and its corresponding fitted m_ij.

The commonly applied goodness-of-fit statistics for this purpose are X² or L² with I(I-1)/2 residual df. Here the X² statistic is restricted to the squared differences between the symmetric observed frequencies,

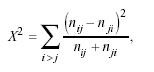
expression known as Bowker’s symmetry test (Bowker, 1948), an extension to IxJ (for I = J > 2) tables of the popular McNemar’s test for tables with related or matched samples (McNemar, 1947). These values are X² = 75.38 for women and X² = 38.66 for men, and the respective L² values are D=81.17 for women and D=45.21 for men, all of them with I(I-1)/2=6 df and none adjusting well (p<.0001).

Discarding a symmetric pattern of responses, a connected hypothesis is the marginal homogeneity model, that consists in comparing the totals or marginal distributions for rows and columns (i.e., if n_i.≈ n_.j), using I-1 residual df for comparisons of I pairs of marginal frequencies or proportions. This hypothesis yields D=77.82 for women and D= 43.32 for men, based on 3 df, leading us in both situations to reject the model with an associated probability p<.0001.

Granting that neither symmetry nor marginal homogeneity models fit this table, we can try a quasi-symmetry model, considering the Caussinus rule (1966): Marginal homogeneity (MH) + Quasi-symmetry (QS) ≈ Symmetry (S). In abbreviated terms the link for these three hypotheses could be expressed in the way H_MH H_QS ≈ H_S, with respective (I-1)+[(I-1)(I-2)]/2 = I(I-1)/2 df. Marginal homogeneity is implied by but does not imply symmetry; so although there was marginal heterogeneity, the S model could not hold. It is perhaps the main reason to find symmetry models hardly fitting data, provided such models are highly structured, with strong assumptions.

The quasi-symmetry model (refered as symmetric association model by Goodman, 1979) fits fairly well for both genders, yielding D=2.50 for women (p=.475) and D=2.24 for men (p=.525) with 3 df each test; their respective fitting criteria are BIC= -16.16 and BIC=-13.73. Once verified that this hypothesis satisfies the two subtables by gender the next step would be to test a quasi-symmetry model for the global table, obtaining a D=4.74 with 6 df, an excellent fit: p=.578 and BIC=-34.63.

Unlike the symmetry model, the QS model does not imply marginal homogeneity, using different parameters for row and column categories. It is a much more "realistic" hypothesis, that fits empirical data more often than other structures (see e.g. McCullagh, 1982; Meiser, Von Eye, and Spiel, 1997). Many useful models are special cases of this one. Some interesting ideas about the formal relationship among the three last hypotheses in tables with ordered categories - as the table used here - may be reviewed in Agresti (1983, 1990).

Association models

We have at least one clue - the QI test - to make us suspect different trends for eating behavior by gender; now it is time to look at such patterns in more depth, to examine the changes with accuracy looking for underlying characteristics within women and men’s data.

In cases where the independence model does not fit well, a reasonable supposition is that there is some degree of dependence - association-among levels of the variables, and could be useful to apply a set of interesting models which allow to restrict bivariate associations between classifications by rows and columns: the association models, which supply several types of association and are especially indicated for ordinal variables, where besides some other hypotheses we need to test the effects of category orderings. This family of models has been developed mainly by Haberman (1974, 1979), Goodman (1979, 1981), Agresti (1984), and Clogg and Shihadeh (1994); Agresti (1990) summarizes their advantages over the nominal-scale models.

The most commonly applied models are the linear-by-linear model and the uniform association model (UA), both of them very similar for practice purposes. These hypotheses require us to assign arbitrary scores for rows and columns to reflect level orderings, being equidistant (uniform) intervals or distances between scores in the second model (therefore a particular case of the first one). This model yields D=8.72 based on IJ-I-J=8 df for women (p=.367, BIC=-41.03), D=15.10 with 8 df for men (p=.057), not significant, and for the global dataset D=23.82 with 16 df (p=.093), a significant fit. This one being the best model found to represent women’s responses, we reproduce the fitted values for this gender in the upper part of the next table, where we can also observe that the UA model respects exactly the empirical marginals of Table 1 (m_i. = n _i. and m_.j =n _.j ):

The association parameter, say φ less for the UA model, just consumed by such parameter). Respectively for the previous tests φ_w=.3873, φ_M=.6289, and the same φ values for both subtables in the global test; these are the average distances among categories in terms of odds ratios (see e.g. Clogg and Shihadeh, 1994). Going one step further, dividing them by their standard errors we could understand better the size of this parameter: z_W = .3873/.0495=7.83 and z_M =.6289/.1115= 5.64; both high and positive z values indicate, in their ordinal meaning, so that the higher the dieting status is in 1982, the higher this status in 1992 tends to be, in an increasing ratio (or multiplicative factor) of _w = exp(.3873) = 1.473 and _M = exp(.6289) = 1.875 for each gender’s changes between adjacent levels, assumptions easily tested by using the common local odds ratios for fitted values in the way.

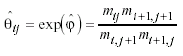
being for example the first of (I-1)(J-1)=9 local odds ratios for women (see Table 2, upper part).

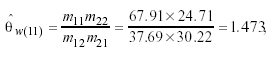
and for men

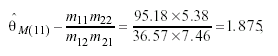
leading again their natural logarithms to the respective φ association parameters log(1.473)=.3783 and log(1.875)=.6289. Moreover, by setting φ = ρ /(1 - ρ²) it is possible to calculate ρ_W = .342 and ρ_M = .483, the estimated correlations between categories if an underlying bivariate normal distribution is supposed.

It is possible to restrict the association structure in some manner. For instance, to analyze tables with the row-variable nominal and the column-variable ordinal, we can apply the so-called row effects models; when finding tables with the row-variable ordinal and the column-variable nominal, a good resource would be the column effects models. For both rows and columns ordinal - as now - we can use the row and column effects models (denoted by RC), where - unlike the linear - by - linear models - row and column parameters replace the row and column frequencies or scores, the nature of the association being described now by local log odds ratios; as Agresti (1990:288) emphasizes, the RC model really is not loglinear, because the log expected frequencies are multiplicative - rather than linear - functions of the model parameters, say m_i for rows and n_j for columns. This model fits very well for women, D=7.02 with (I-2)(J-2)=4 df (p=.135, BIC=-17.85), and for men, D=3.27 based on 4 df (p=.514, BIC=-18.02). So the RC model is a more appropriate structure to represent men’s data.

Association-Marginal models

The last methodological approach to be proposed in this work can be viewed as a mixture of two other ones, loglinear and marginal models, named simultaneous modeling. Modern researchers may use the loglinear approach to analyze the association between response categories inside a contingency table and use also the marginal approach to model the information provided by totals of rows and columns. This new method is also labelled association-marginal models (AM), which simultaneously employs cell frequencies and marginal distributions to estimate parameters and to describe the effects of possible factors or covariates, all this within a flexible frame. Main outlines of AM models can be seen in works by Becker (1994), Lang and Agresti (1994), Bergsma (1997), and Lang and Eliason (1997).

Before applying AM models it is interesting to test a simple marginal hypothesis, that claims similar odds ratios for rows and columns. Using the observed marginal values in Table 1 these empirical odds ratios can be obtained - a recent work about the great usefulness of odds ratios is provided by Rudas (1998)- for women’s data

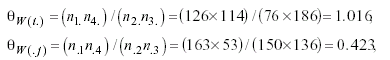
and with respect to men’s subtable

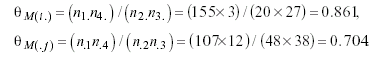
As a primary strategy to compare them, dividing both odds ratios within each gender, 1.016/.423 = 2.402 and 861/.704 = 1.223, a quotient far from 1 in the case of women can be appreciated, which reveals a very probable lack of fit for the marginal hypothesis, but a value close to 1 with the totals provided by men, indicating high similarity between these odds ratios and, in advance, a likely good fit of such hyphotesis.

The next stage consists of choosing a complementary loglinear model to combine with the marginal hypothesis in order to get a better fit. Perhaps the most interesting model for the actual men’s data is the quasi-symmetry one applied above (a realistic structure to explain data, we said), that yielded a minimum D=2.24 with 3 df. Adding to it the marginal hyphotesis (i.e., a restriction about θ_M(i.) ≈ θ_M(.j)), we achieve an excellent fit: D=2.33 based on 4 df, being p=.675 and BIC=-18.96. The estimated values for this model are in the lower part of Table 2.

Since the marginal restriction forces both odds ratios to be equal, now

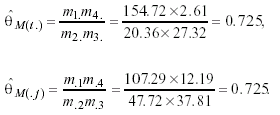
With this last modeling structure the deviance has only increased 0.09 points, but on the other hand we have recovered 1 df due to a particular feature of the mixed parameterization implied by the AM models. By means of this structure we can describe fairly the trends for men’s behavior: more stability than women with time - compare the respective totals: men present always the highest and the lowest frequencies related to the same categories - and a strong QS-association type among responses.

Discussion

Taking into account that eating disorders doubtless are one of the main concerns for researching in several sciences, we may wonder if enough information is obtained from the traditional exploitation of the scarce available data compiled by means of strict longitudinal studies. Throughout this work we have found different statistical models to select depending on a grouping variable, gender in the study of reference; men and women’s eating behavior must not be analyzed or described using the same patterns, as this modeling session has attempted to show.

We have examined first global aspects of the data distribution by applying the Independence, Symmetry, Marginal and related models, and then particular features of change analysis inside the table by using the Association models, to finish with a profitable mixture of both, the Association-Marginal models.

Not only the quantity of differences is relevant, but also the direction or deep meaning of them, what a simple and lonely χ² test usually cannot detect. The main thing to be evaluated here was a different trend in - for instance - dieting behavior depending on a particular trait, gender, which is, on the other hand, the categorical variable used more often in the Social and Health Sciences. An excellent illustration for this issue in the modern research is offered by Kagan (1998).

The final words of Heatherton et al. (1997:124) about "... the maintenance or change in eating attitudes and behaviors is an important goal for future research", underline the great interest in new methodological lines - as CDA - which allow the researcher to take the maximum information from real data, to obtain acceptable explanations about human behavior by means of testing different models for the analysis of stability and change, helpful methods derived from the GLMs framework, as - besides those already applied above - for instance the loglinear Rasch models for multivariate longitudinal responses (Meiser, 1996; Agresti, 1997; Rabadán, Ato y Galindo, 1999) or the latent class models (Hagenaars, 1993; Heinen, 1996). In spite of the small amount of longitudinal works about eating behaviors due to the probable reasons we pointed out before, the development and diffusion of these new analytical tools could encourage more researchers to look for such studies. Surely there are yet amounts of interesting behavioral patterns which a systematic application of the CDA methods could bring to light.

Agresti, A. (1983). Testing marginal homogeneity for ordinal categorical variables. Biometrics, 39, 505-510.

Agresti, A. (1984). Analysis of Ordinal Categorical Data. New York,NY: Wiley.

Agresti, A. (1990). Categorical Data Analysis. New York, NY: Wiley.

Agresti, A. (1997). A Model for Repeated Measurements of a Multivariate Binary Response. Journal of the American Statistical Association, 92, 315-321.

Ato, M., Rabadán, R., y Galindo, F. (1999). Dos enfoques analíticos del diseño con grupo de control no equivalente para variables dependientes categóricas. Psicothema, 11(3), 663-78.

Becker, M. (1994). Analysis of cross-classifications of counts using models for marginal distributions: An application to trends in attitudes on legalized abortion. Sociological Methodology, 24, 229-265.

Bergsma, W. (1997). Marginal Models for Categorical Data. Doctoral dissertation (published as WORC paper). Tilburg University, Holland.

Bishop, Y., Fienberg, S., & Holland, P. (1975). Discrete Multivariate Analysis: Theory and Practice. Cambridge, MA: The MIT Press.

Bowker, A. (1948). A test for symmetry in contingency tables. Journal of the American Statistical Association, 43, 572-574.

Caussinus, H. (1966). Contribution a l’analyse statistique des tableaux de correlation. Annales de la Faculté des Sciences de l’Universitat‚ de Toulouse, 29, 77-182.

Clogg, C.C., & Shihadeh, E. (1994). Statistical Models for Ordinal Variables. Thousand Oaks, CA: Sage.

Goodman, L. (1972). A general model for the analysis of surveys. American Journal of Sociology, 78, 1135-1191.

Goodman, L. (1978)(ed. J. Magidson). Analyzing Qualitative/Categorical Data. Cambridge, MA: ABT Books.

Goodman, L. (1979). Simple models for the analysis of association in cross-classifications having ordered categories. Journal of the American Statistical Association, 74, 537-552.

Goodman, L. (1981). Association models and canonical correlation in the analysis of cross-classifications having ordered categories. Journal of the American Statistical Association, 76, 320-334.

Haberman, S.J. (1974). Loglinear models for frequency tables derived by indirect observation: maximum likelihood equations. Annals of Statistics, 2, 911-924.

Haberman, S.J. (1979). Analysis of Qualitative Data. II: New Developments. New York, NY: Academic Press.

Hagenaars, J. (1993). Loglinear Models with Latent Variables. Newbury Park, CA: Sage.

Heatherton, T.F., Mahamedi, F., Striepe, M., Field, A.E., & Keel, P. (1997). A 10-year longitudinal study of body weight, dieting, and eating disorder symptoms. Journal of Abnormal Psychology, 106, 117-125.

Heinen, T. (1996). Latent Class and Discrete Latent Trait Models: Similarities and Differences. Newbury Park, CA: Sage.

Kagan, J. (1998). The Quiet Return of Categories. Social Research, 65, 449-461.

Lang, J., & Agresti, A. (1994). Simultaneously modelling joint and marginal distributions of multivariate categorical responses. Journal of the American Statistical Association, 89, 625-632.

Lang, J., & Eliason, S. (1997). Application of association-marginal models to the study of social mobility. Sociological Methods & Research, 26, 183-212.

McCullagh, P. (1982). Some applications of quasi-symmetry. Biometrika, 69, 303-308.

McCullagh, P., & Nelder, J. (1989). Generalized Linear Models, 2nd ed. London: Chapman & Hall.

McNemar, Q. (1947). Note on the sampling error of the difference between correlated proportions or percentages. Psychometrika, 12, 153-157.

Meiser, T. (1996). Loglinear Rasch models for the analysis of stability and change. Psychometrika, 61, 629-645.

Meiser, T., Von Eye, A., & Spiel, C. (1997). Loglinear symmetry and quasi-symmetry models for the analysis of change. Biometrical Journal, 39, 351-368.

Nelder, J., & Wedderburn, R. (1972). Generalized linear models. Journal of the Royal Statistical Society, series A, 135, 370-384.

Rabadán, R., Ato, M., y Galindo, F. (1999). Extensiones del modelo loglineal de Rasch para el análisis de datos categóricos. Metodología de las Ciencias del Comportamiento, 1(1), 61-79.

Raftery, A. (1986). Choosing models for cross-classifications. American Sociological Review, 51, 145-156.

Raftery, A. (1995). Bayesian model selection in social research. In P. Marsden, ed.: Sociological Methodology 1995, 25, 111-163.

Rudas, T. (1998). Odds ratios in the analysis of contingency tables. Thousand Oaks, CA: Sage.

Sánchez-Carracedo, D., y Saldaña, C. (1998). Evaluación de los hábitos alimentarios en adolescentes con diferentes índices de masa corporal. Psicothema, 10(2), 281-92.

Vermunt, J. (1997). LEM: A general program for the analysis of categorical data, 2nd draft. Unpublished monograph. Tilburg University, Holland.

Wilks, S. (1935). The likelihood test of independence in contingency tables. Annals of Mathematical Statistics, 6, 190-196.