La revista Psicothema fue fundada en Asturias en 1989 y está editada conjuntamente por la Facultad y el Departamento de Psicología de la Universidad de Oviedo y el Colegio Oficial de Psicología del Principado de Asturias. Publica cuatro números al año.
Se admiten trabajos tanto de investigación básica como aplicada, pertenecientes a cualquier ámbito de la Psicología, que previamente a su publicación son evaluados anónimamente por revisores externos.
Psicothema, 1993. Vol. Vol. 5 (nº 1). 177-182
Miguel A. RUIZ y Rafael SAN MARTIN
Facultad de Psicología. Universidad Autónoma de Madrid.
El problema de la determinación del número de factores que deben ser retenidos en un Análisis Factorial no ha sido resuelto aún de forma satisfactoria. Habitualmente se recurre a reglas como la K1, por estar implementadas en los paquetes de cálculo estadístico. Sin embargo, existen reglas, como el MAP, más eficaces y también de fácil implementación. Aquí, se presenta un pequeño programa para su cálculo con uno de los paquetes más difundidos.
Palabras clave: Análisis Factorial; Número de factores.
An implementation of the MAP procedura for determining the number of factors. How many factors to retain is a common problem in Factor Analysis that hasn't been solved yet. The eigenvalues greater than 1 rule is commonly used since its a built-in option in most statistical packages. Nevertheless, there are other more effective rules available, like MAP, that can also be easily worked out. Here we present a program towards computing the MAP procedure, to be executed inside one of the most widely used packages.
Key words: Factor Analysis; Number of factors.
El problema de determinar el número de factores que deben ser retenidos en un análisis factorial de Factor Común no es nada novedoso. De hecho existen diversas reglas que ayudan a designar el número de factores más adecuado, y algunas de ellas han sido incluidas en los paquetes de análisis estadístico más extendidos. Este es el caso de la Prueba de Sedimentación (ScreeTest, Cattell, 1966; Cattell y Vogelman, 1977), la regla de Kaiser Guttman (Guttman, 1953; Kaiser, 1960, 1961), la prueba de Bartlett (1950, 1951) y la prueba de bondad de ajuste de Jöreskog (1966).
Diversos estudios han analizado y comparado el comportamiento de estas reglas en distintas condiciones de complejidad factorial, número relativo de factores y tamaño de las muestras, encontrando problemas en la utilización de todas ellas (Velicer y Fava, 1987; Zwick y Velicer, 1982; Hakstian, Rogers y Cattell, 1982, Ruiz, 1992), y una tendencia generalizada a la sobreestimación del número de factores. En algunos de estos estudios (Zwick y Velicer, 1982, 1986) se ha estudiado el comportamiento relativo de otro procedimiento, el MAP (Minimum Average Partial method, Velicer, 1976), que parece comportarse sensiblemente mejor que los anteriores.
Sin embargo, el MAP no está implementado en ningún paquete estadístico. En este artículo proponemos un procedimiento de cálculo con el módulo matricial (procedimiento MATRIX) del SPSSX.
FUNDAMENTACION
Velicer (1976) propone un procedimiento para la estimación del número de factores, que utiliza como criterio las correlaciones parciales entre las variables originales tras haber eliminado de ellas la información reproducida por los factores ya extraídos.
Este procedimiento puede utilizarse tanto con el modelo de Análisis Imagen (ver Mulaik, 1972), como con la extracción de Componentes Principales utilizada como modelo de Análisis Factorial (Horst 1955: Van de Geer 1971; Velicer & Jackson, 1990) en el que solamente se desea explicar la variabilidad común entre las variables, de manera similar a un modelo de Factor Común, y por tanto se persigue retener un número de factores menor que el número de variables.
Mediante un procedimiento iterativo, se pueden ir extrayendo de la matriz de correlaciones muestral las correlaciones reproducidas por la estructura factorial, según vienen reflejadas en los autovectores de la autodescomposición por Componentes Principales. De manera que la matriz Rr de la fórmula
Rr = R-AA' (1)
representa una matriz de correlaciones reducida, de la que se han eliminado las correlaciones reproducidas por los autovectores contenidos en la matriz de estructura A. Esta matriz Rr es equiparable a la matriz residual del Análisis Factorial.
Á partir de la matriz redisidual Rr pueden calcularse las correlaciones parciales entre las variables mediante la fórmula.
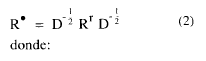
donde:
D = diagRr (3)
Una vez calculadas mediante (2) las correlaciones parciales de la matriz de correlaciones reducida, es fácil calcular un estadístico que promedie los cuadrados de todos lo elementos de R*, menos su diagonal, mediante la fórmula
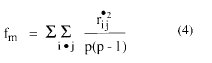
Si se están estudiando p variables, pueden extraerse m (=p) autovectores de la matriz de correlaciones. Los distintos autovectores van incorporándose sucesivamente a la matriz A, eliminado así su efecto, uno tras otro, de la matriz de correlaciones, para dar lugar a la serie de matrices residuales. Sobre esta serie se calcula el estadístico fm, que tomará un valor distinto dependiendo del número de autovectores que han sido eliminados de la matriz de correlaciones original. Así, fm puede ser calculado desde m=1 hasta p-1, ya que cuando m=p la matriz residual es una matriz nula.
La función fm presenta un mínimo para el número idóneo de componentes por eliminar, que se corresponde con el número de factores que deben ser retenidos (Velicer, 1976).
Adicionalmente, Velicer propone un estadístico de comparación, que se calcula a partir de los elementos de R:
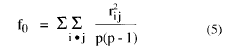
Si f1 < f0 no deberá extraerse ningún factor.
Este procedimiento presenta la ventaja de eliminar de la posible extracción aquellos factores que representan a una única variable, y es un limite para el número de factores por retener.
Según Velicer (1976) y Zwick y Velicer (1982, 1986), el procedimiento se comporta mejor que la regla K1 y la Prueba de Sedimentación, y tiende a la infraestimación del número de factores cuando éstos están pobremente definidos (saturaciones menores que .5) y la proporción de variables por factor es elevada.
PROCEDIMIENTO
Gracias al nuevo módulo de álgebra matricial que incluye el paquete SPSSX (versión 4.1 de mainframe) resulta bastante simple implementar el MAP, para ejecutarlo a lo largo de una sesión de trabajo. A continuación se presenta un listado de las órdenes necesarias1 . Estas pueden ser recogidas en un fichero y ser incluidas con el comando INCLUDE en una sesión interactiva.
Supongamos que estamos trabajando con un fichero de sistema que tiene definidas 10 variables, denominadas VAR1 a VAR1O. Las órdenes del programa deben ser:
Si no se dispone de mucha memoria de trabajo en la cuenta (por debajo de los 4 Megas), será mejor ejecutar todo el programa por lotes, para lo que habrá que incluir las líneas de definición del fichero de datos en el fichero del programa.
Por ejemplo, si disponemos de un fichero denominado nombre fich, que contiene 10 variables en formato libre, deberemos escribir antes de la línea 1:
DATA LIST FILE 'nombre fichero' FREE/ VAR1 TO VAR1O
Si en lugar de trabajar con los datos originales (puntuaciones directas en las variables) se desea trabajar con una matriz de correlaciones creada con anterioridad, y almacenada en el fichero nombre mat deben introducirse las siguientes modificaciones en las primeras líneas.
MATRIX DATA VAR X1 TO X3 / FILE 'nombre mat’ / CONT COR
FACTOR MATRIX IN ( COR = * ) OUT ( COR = COR1)
Otra posibilidad es llevar a cabo la extracción correspondiente al modelo de Análisis Imagen (Guttman, 1953; Joreskog, 1962, 1969) con lo que la matriz que debemos analizar ya no es la matriz de correlaciones sino la matriz
S-1 RS-1 (6)
Bastará incluir las órdenes
COMP = SQRT (( MDIAG ( DIAG ( INV ( CR ) ) ))**(-1))
COMP CR=S**(-1)* CR*S**(-1)
entre las líneas 6 y7.
EJEMPLO
Sea la matriz de correlaciones poblacional

que puede ser definida por la estructura factorial
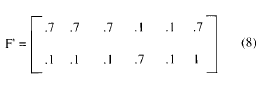
En esta estructura tenemos un primer factor definido por 4 variables, un segundo factor definido únicamente por 4 variables y una variable (la 5ª) que no satura en ninguno de los dos factores. Si esta estructura fuera conocida de antemano, cualquier analista descartaría la 5ª variable por no contener información relevante, dada su baja fiabilidad, así como la 4ª por representar un contenido de información poco común al resto de las variables.
Si llevamos a cabo un Análisis Factorial de Factor Común, con una extracción de Componentes Principales, la regla K1, que en el SPSS estará vigente por defecto, retendrá ambos factores, ya que los primeros autovalores de la matriz de correlaciones serán λ1 = 2.5, λ2, =1.02 y λ3 = .91. La estructura factorial obtenida, tras una rotación ortogonal será:
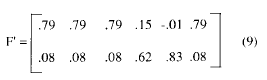
Aunque normalmente la literatura sobre el tema recomienda retener los factores representados al menos por tres variables, a la vista de la estructura obtenida en (9) nos podíamos sentir tentados a retener el segundo actor. Y lo que es peor, no descartaríamos la 5ª variable que tendría una comunalidad de 0.42, muy por encima de su comunalidad teórica de 0.02.
Si aplicamos el MAP la función obtenida será
fm = 0.49 0.108 1.4x1028 (10)
El mínimo de la función corresponde al primer valor de la misma con lo que tan sólo retendríamos un factor, detectando la falta de información común contenida en la 4ª variable, y la inviabilidad de la 5ª variable. Como puede observarse, los últimos valores de la función no están definidos. Esto es debido a que pueden aparecer números negativos en la diagonal de la matriz Rr y sus raíces cuadradas no pueden ser calculadas. En cualquier caso, el mínimo es alcanzado siempre antes de llegar a este punto.
Aplicada la función MAP a la matriz de Análisis Imagen, el resultado es
fm = 0.071 0.124 1.235 1.478 1.768 2.269 (11)
que nos llevaría a la misma conclusión anterior. Adicionalmente, el valor del estadístico de comparación, definido en (6), será fo = 0.107.
CONSIDERACIONES FINALES
Para todos nosotros resulta imprescindible disponer de herramientas informáticas, que posibiliten el análisis de las grandes masas de datos con las que trabajamos en la investigación en psicología. Afortunadamente, existe un número suficientemente extenso de estas herramientas, que abarcan la mayoría de los problemas que debemos afrontar.
Sin embargo, la mayoría de los paquetes ofrecen soluciones cerradas al usuario, en la construcción de los algoritmos de estimación. Sería imposible diseñar programas a medida para cada uno de los análisis particulares, pero no debemos abandonarnos en el análisis rutinario a la manera que esté implementado el programa, y desarrollar un exceso de confianza hacia los programas.
Por ello hay que dar la bienvenida a herramientas más versátiles, que nos permitan, al menos, probar otros algoritmos y reglas de decisión que puedan irse desarrollando.
En el caso del Análisis Factorial Exploratorio, los algoritmos utilizados no han variado desde su primera inclusión en los paquetes estadísticos más difundidos. A pesar de tratarse de una técnica veterana, aún no ha perdido vigencia, como demuestra que se haya dedicado todo el número 1 de 1990 de la revista Multivariate Behavioral Research a este tema. Debemos aprovechar la posibilidad de utilizar procedimientos como el MAP, el Parallel Analysis (Horn, 1965; Humphreys y Montanelli, 1975; Montanelli y Humphreys, 1976), el procedimiento de Rango mínimo (Ten Berge y Kiers, 1991) el Conjoint Analysis (Umesh y Mishra, 1987) o las correcciones por desatenuación para los coeficientes de correlación (Hakstian, Schroeder y Rogers, 1989) que sean más sensibles a las particularidades de nuestro trabajo.
1. Las líneas del programa están numeradas para poder discutirlas en el texto. Esta numeració sólo tienen sentido en este contexto y debe ser eliminada para su ejecución.
2. Esta Orden evita que el programa aborte al intentar calcular la raíz cuadrada de un número negativo.
REFERENCIAS
Bartlett, M. S. (1951). A further note on tests of significance in factor analysis. British Journal of Psychology, Statistical Section, 4, 1-2 .
Bartlett, M. S. (1950). Tests of significance in factor analysis. British Journal of Psychology, 3, 77-85.
Cattell, R. B. (1966). The Scree Test for the Number of Factors. Multivariate Behavioral Research, 1, 245 -276.
Cattell, R. B. y Vogelmann, S.A. (1917). A Comprehensive Trial of the Scree and KG Criteria for Determining the number of Factors. Multivariate Behavioral Research. 12, 289-325 .
Guttman, L. (1953). Image theory for the structure of quantitative variates. Psychometrika, 18, 277-296.
Hakstian, A. R., Rogers, W.T. y Cattell, R.B. (1982) .The behavior of number of factor rules with simulated data. Multivariate Behavioral Research, 17, 193-219.
Horn,J. L. (1965). A rationale and test for the number of factors in factor analysis. Psychometrika, 30, 179-185.
Horst, P. (1967). Factor analysis of data matrices. NY: Holt, Rinehart and Winston.
Humphreys, L. G. y Montanelli, R. G. (1975). An investigation of the parallel analysis criterion for determinig the number of common factors. Multivariate Behavioral Research, 10, 193-206 .
Joreskog, K. G. (1969). Efficient estimation in image factor analysis. Psychometrika, 34,51-75.
Joreskog, K. G. (1966). Testing a simple structure hypotesis in factor analysis. Psychometrika, 31, 165-178.
Joreskog, K. G. (1962). On the statistical treatment of residuals in factor analysis. Psychometrika, 27, 335-354.
Kaiser, H. F. (1961). A note on Guttman's lower bound for the number of common factors. British Journal of Statistical Psychology. 14 (1), 1.
Kaiser, H. F. (1960) . The application of electronic computers to factor analysis. Educational and Psychological Measurement, 20,141-151.
Montanelli, R. G. y Humphreys, L. G. (1976). Latent roots of latent data correlation matrices with squared multiple correlations on the diagonal: A Monte Carlo study. Psychometrika, 41, 341-348.
Mulaik, S. A. (1972). The Foundations of Factor Analysis. NY: McGraw-Hill. Multivariate Behavioral Research (1990), 25.
NoruSis/SPSS inc. (1988). SPSS-X User's Guide (3rd edition) J. Chicago, EL: SPSS Inc.
Ruiz y San Martín (1992). Una simulación sobre el comportamiento de la regla K1 en la estimación del número de factores. Psichotema, 4, 543-550.
Ten Berge, J. M. F. y Kiers, H. A. L. (1991). A numerical approach to the approximate and the exact minimum rank of covariance matrix. Psychometrika, 56, 309-315.
Umesh, U. N. y Mishra, S. (1990). A Monte Carlo investigation of conjoint analysis index-of fit: Goodness of fit, significance and power. Psychometrika, 55, 33-44.
Van der Geer, J. P. (1971). Introduction to multivariate analysis for- the social sciences. SF: Freeman.
Velicer, W. F. y Jackson, D. N. (1990). Component Analysis versus Common Factor Analysis: some issues in selecting an appropiate procedure. Multivariate Behavioral Research, 25, 1-28 .
Velicer, W. F. y Fava, F. L. (1987). An evaluation of the effects of variable sampling on Component, Image and Factor Analysis Multivariate Behavioral Research, 22, 193-209 .
Velicer, W. F. (1976) . Determining the number of components from the matrix of partial correlations. Psychometrika, 41, 321-327.
ZwiCk, W. R. y Velicer, W. F. (1982). Factors influencing four rules for determining the number of components to retain. Multivariate Behavioral Research, 17, 253-269.
Zwick, W. R. y Velicer, W. F. (1986). Comparison of five rules for determining the number of componentes to retain. Psychological Bulletin, 3, 432-442.