COMPARACIÓN ENTRE LAS MEDIDAS DE ÁREA, EL ESTADÍSTICO DE LORD Y EL ANÁLISIS DE REGRESIÓN LOGÍSTICA EN LA EVALUACIÓN DEL FUNCIONAMIENTO DE LOS ITEMS

Mª Dolores Hidalgo Montesinos y José Antonio López Pina

Universidad de Murcia

El presente estudio pretende identificar las condiciones bajo las cuales la medida de área con signo Z(AES), la medida de área sin signo Z(AEA), el estadístico de Lord y el análisis de regresión logística (RL) detectan la presencia de funcionamiento diferencial del ítem (FDI). Las condiciones manipuladas fueron: tamaño muestral, cantidad y tipo de FDI, presencia o no de impacto, porcentaje de items con FDI en el test y nivel de significación. Los resultados encontrados muestran que el estadístico de Lord y Z(AEA) son bastante eficaces en la detección correcta de FDI uniforme, no uniforme y mixto. Por otro lado, el procedimiento de RL fue eficaz en la detección del FDI no uniforme y mixto, pero no en la del FDI uniforme. El estadístico de Lord, Z(AES) y Z(AEA) obtuvieron tasas de falsos positivos más elevadas que RL, principalmente cuando el tamaño muestral y el porcentaje de items con FDI en el test fueron elevados. Esto también ocurrió cuando la cantidad de FDI fue alta.

An comparison of the Area Methods, Lord’s chi-square test and Logistic Regression Analysis for Assesing Differential Item Functioning. The present study compared the performance under different conditions of the signed area measure Z(AES), the unsigned area measure Z(AEA), Lord’s chi-square test and the logistic regression analysis (LR) on detection of differential item functioning (DIF). Sample size, amount and type DIF, difference in the group trait level averages, percent of DIF items test and significance levels were manipulated. The results show that Lord’s test and Z(AEA) were effective in assessing uniform, non-uniform and mixed DIF. The LR procedure was low power for detecting uniform DIF, however it was able to detect non-uniform and mixed DIF. When the sample size, amount of DIF and percent of DIF items were larger high number of false positives were obtained using the Lord’s statistic, Z(AES) and Z(AEA).

Una de las críticas más importantes a los tests psicométricos ha sido afirmar que están sesgados, es decir, que favorecen injustamente a los sujetos de un grupo (p.e. clase social alta, varones...) sobre los sujetos de otro grupo (p.e. clase social baja, mujeres...) identificando erróneamente diferencias entre grupos. Cuando se utiliza un test en la evaluación de cualquier rasgo o habilidad psicológica es de esperar que éste sirva al propósito por el cual fue construido y proporcione medidas fiables y válidas acerca de la manifestación del rasgo en los sujetos. Así, si se administra un test a dos grupos de sujetos que difieren en el rasgo evaluado, estas diferencias (impacto) deben ser detectadas por el test. Del mismo modo, si los grupos no difieren (no impacto) las puntuaciones obtenidas en el test deben reflejar la igualdad entre grupos. Esto se traduce a que las propiedades psicométricas del test y por ende de los items que lo conforman sean invariantes a través de distintos grupos o muestras de una misma población. En ocasiones, y contrario a lo esperado, algunos de los items de un test pueden funcionar diferencialmente en los grupos en los que se han administrado, siendo necesario estudiar este hecho, que en el ámbito psicométrico se ha denominado Funcionamiento Diferencial del Item (FDI). El FDI se produce cuando, en dos o más grupos equivalentes, la probabilidad de obtener una respuesta correcta, dado un nivel de habilidad es diferente para cada uno de dichos grupos (Scheuneman, 1979).

Normalmente, en los estudios de FDI, los sujetos son clasificados en dos grupos: Focal (F) y Referencia (R). Se denomina grupo focal al grupo objeto de análisis, casi siempre un grupo minoritario. Por contra, el grupo de referencia se toma como grupo base o de comparación, casi siempre un grupo mayoritario. La variable de agrupamiento podría ser cualquiera sociodemográfica (sexo, etnia, edad, nivel educativo...) en la que se sospeche que las propiedades psicométricas de los items pueden diferir.

Mellenbergh (1982) definió dos tipos de FDI: Uniforme cuando la probabilidad de responder correctamente a un ítem es mayor en un grupo que en otro y No uniforme cuando esta probabilidad es mayor en un grupo que en otro, hasta un nivel de habilidad dado, y a partir de dicho nivel de habilidad las probabilidades se invierten siendo menores en el primer grupo que en el segundo. En este último caso se dan dos situaciones: No uniforme propiamente dicho cuando las diferencias en probabilidad entre los grupos sometidos a análisis se cancelan, y Mixto cuando estas diferencias no se anulan.

Las técnicas propuestas para evaluar el FDI se pueden clasificar como (Millsap y Everson, 1993): a) Métodos de Invarianza Condicional Observada (ICO) que utilizan las puntuaciones observadas en el test como variable de equiparación. Aquí se podría incluir entre otros el estadístico de Mantel-Haenszel (Holland y Thayer, 1988), los modelos logit (Mellenbergh, 1982) y el análisis de regresión logística (Rogers y Swaminathan, 1993; Swaminathan y Rogers, 1990); y b) Métodos de Invarianza Condicional No observada (ICN), donde se trabaja a partir de las puntuaciones de habilidad estimadas según algún modelo de medida. En la Teoría de la Respuesta a los Items se han propuesto métodos de comparación de parámetros (Lord, 1980), medidas de área (Cohen, Kim y Baker, 1993; Kim y Cohen, 1991; Raju, 1988, 1990) y métodos basados en la comparación de modelos (Thissen, Steinberg y Wainer, 1988, 1993).

Ante tal cantidad de aproximaciones, puede resultar útil conocer qué procedimientos son los más eficaces en la evaluación del FDI y bajo qué condiciones. Desde los métodos de ICO, el estadístico de Mantel-Haenszel (MH), por su sencillez de cálculo e interpretación, ha sido uno de los procedimientos más utilizados e investigados. Sin embargo, aunque es eficaz en la detección de FDI uniforme, es incapaz de detectar correctamente el FDI no uniforme, salvo cuando se aplican variaciones iterativas del mismo (Clauser, Mazor y Hambleton, 1993; Fidalgo, 1996). El análisis de regresión logística (RL) más complejo y costoso de realizar, es más potente en la identificación correcta de FDI no uniforme que el estadístico de MH. Las ventajas del análisis de RL no sólo radican en lo anteriormente comentado, sino que frente al procedimiento de MH, RL establece una relación funcional entre la respuesta al ítem y la variable de comparación. Una característica de los métodos ICO es que no establecen ningún supuesto sobre el modelo de medida subyacente a los datos del test. Estos métodos son aplicados tomando las puntuaciones observadas en el test. Por contra, algunos de los métodos de ICN se aplican una vez ajustado un modelo de TRI. Desde un punto de vista teórico resulta más apropiado trabajar bajo este tipo de modelos dadas las ventajas estadísticas que se derivan del ajuste de los mismos (Lord, 1980). Sin embargo, en la práctica no siempre es posible implementar estos modelos dado que el buen ajuste de los mismos requiere, entre otras cosas, grandes muestras de sujetos que rara vez se dispone en la investigación aplicada sobre FDI. Es más, estos métodos son menos fáciles de aplicar que MH o RL.

Una parte de los trabajos sobre FDI se han ocupado de estudiar el acuerdo entre los métodos de ICO y de ICN (Hambleton y Rogers, 1989; Hidalgo, 1995; Navas y Gómez, 1994; Raju, 1990). Así, Hambleton y Rogers (1989) encontraron que el estadístico de MH y las medidas de área proporcionan resultados más o menos similares en la detección correcta de FDI uniforme. Mientras que, cuando el FDI fue no uniforme las medidas de área identificaron correctamente mayor cantidad de items con FDI que el estadístico de MH. Raju (1990) encontró que las medidas exactas de área sin signo se mostraron más precisas en la evaluación del FDI frente a las medidas de área con signo y el estadístico de MH. De los trabajos de Hambleton y Rogers (1989) y Raju (1990) se deduce la preferencia de los procedimientos basados en TRI frente a métodos de ICO tales como MH. Sin embargo, pocos son los trabajos que han comparado RL (más potente que MH en la detección del FDI no uniforme) y los procedimientos de TRI (Hidalgo, 1995). Navas y Gómez (1994) compararon entre otras técnicas RL y las medidas exactas de área de Raju en la detección de FDI uniforme, encontrando que ambos procedimientos detectan por igual la presencia de FDI. No se conoce el acuerdo entre estas técnicas en la evaluación del FDI no uniforme y tampoco ha sido estudiado su comportamiento en distintas condiciones de porcentaje de items con FDI en el test, cantidad de FDI, y tipo de FDI.

El presente trabajo pretende identificar las condiciones (tamaño muestral, porcentaje de items con FDI en el test, cantidad y tipo de FDI) bajo las cuales el análisis de RL, las medidas exactas de área de Raju (1990) y el estadístico de Lord (1980) detectan mejor la presencia de FDI. Para ello se realizó un estudio de simulación.

Regresión Logística

La ecuación general para un modelo de RL vendría dada por (Hosmer y Lemeshow, 1989):

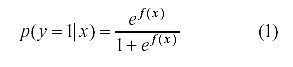
donde y es la variable de respuesta, p(y=1| x) es la probabilidad de obtener una respuesta correcta (probabilidad de éxito) condicionado a x, x es el vector de variables predictoras y f (x)= β₀ + β₁ x₁ + β₂ x₂ + ...+β_p x_p, siendo p el número de variables predictoras. El modelo no lineal de la ecuación 1 puede transformarse a un modelo lineal aditivo, efectuando sobre la variable criterio una transformación logit. En el estudio del FDI, f (x) = β₀ + β₁ H + β₂ G + β₃HG. Donde β₀ es el efecto total de la dificultad del ítem, β₁ es el efecto de la variable H, que se define como la puntuación observada en el test, β₂ es el efecto de la variable grupo (G) y β₃ es el efecto de la interacción habilidad x grupo (HG). Un ítem mostrará FDI uniforme si β₂≠ 0 y β₃ = 0, y FDI no uniforme si β₃ ≠ 0, independientemente que β₂ sea igual a cero o no (Swaminathan y Rogers, 1990). Estas hipótesis, normalmente, se prueban utilizando el estadístico de Wald que permite probar la significación de los pesos β comparando el valor estimado (_p) para un peso p con su error típico (SE (_p)) según la siguiente expresión:

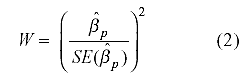
que sigue una distribución χ²1

Medidas de Raju

En la TRI se han propuesto un conjunto de medidas basadas en el cálculo del área entre la Curva Característica del Item (CCI) en el grupo focal y la CCI en el grupo de referencia. Raju (1988, 1990) propone dos medidas de área exactas (con signo y sin signo) disponibles en los modelos de 1-p, 2-p y 3-p que permiten probar su significación estadística a través de una prueba Z. La expresión general de estas medidas, basadas en la integración continua, viene dada por:

donde P_R(θ) y P_F(θ) representan las probabilidades de responder correctamente al ítem i en cada uno de los grupos (R y F). La función f puede especificarse con signo o sin signo. En el primer caso se obtendría la medida de área exacta con signo (AES), y en el segundo una medida de área exacta absoluta (AEA). La expresión general de la ecuación 3 adopta distintas formas según el modelo de TRI con el que se este trabajando, y si se cumplen o no ciertas condiciones en los parámetros de los items. Así, en el modelo de 2-p, Raju (1988, 1990) define el área con signo como AES= (_iF -_iR) y el área absoluta como AEA= |_F -_R| cuando los parámetros de discriminación son iguales en los grupos focal y de referencia o AEA= | H_i | cuando son distintos. El valor H(i) se obtiene según:

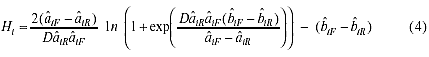
Las pruebas estadísticas para las medidas de Raju (1988) son:

Prueba de significación para AES. Se asume que AEA se distribuye normalmente. De este modo, para probar estadísticamente si las diferencias entre dos CCIs son significativas se puede utilizar la siguiente prueba Z (Raju, 1990, p. 202):

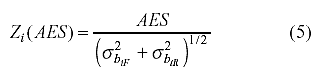
donde σ²_biF y σ²_biR vienen dadas en Raju (1990, pp.200).

Prueba de significación para AEA. No es posible establecer el supuesto de normalidad para las medidas AEA. Cuando â_iR ≠ â_iF Raju (1990, pp. 203) recomienda que la prueba de significación se realice sobre H y no sobre su valor absoluto. Así,

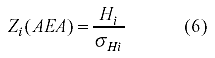
Cuando â_iR = â_iFse utiliza la prueba estadística de la ecuación 5.

A fin de probar la significación estadística de estas medidas exactas de área, el valor Z se compara con el valor teórico correspondiente a la distribución normal tipificada, dado el nivel de confianza prefijado por el investigador. Si el valor Z observado es mayor o igual que el valor teórico, el ítem bajo estudio presenta FDI. En caso contrario, se considera que el ítem no presenta FDI.

Procedimiento de Lord

Un ítem funciona diferencialmente en dos grupos si los parámetros que lo definen varían a través de los grupos. Lord (1980) propone un estadístico que somete a comprobación esta hipótesis. Este estadístico viene dado por (Lord, 1980, p. 233):

donde V es el vector de diferencias entre los parámetros estimados para un ítem en el grupo de referencia y los parámetros estimados para ese mismo ítem en el grupo focal. Bajo el modelo de 2-p, V’ es:

y S^-1, es la inversa de la matriz de varianza-covarianza asintótica para los vectores de diferencias entre parámetros.

El estadístico propuesto por Lord, bajo la hipótesis nula, sigue una distribución χ² con dos grados de libertad. Un ítem presenta FDI si el valor observado LORD - χ² es mayor que el valor teórico asociado χ²₂ al nivel de significación establecido.

Método

Condiciones experimentales

Se han seleccionado tres tamaños muestrales de 250, 500 y 1000 sujetos tanto para el grupo focal como para el grupo de referencia y un tamaño de test fijo (75 items). Para cada uno de los tamaños muestrales se generaron dos distribuciones de habilidad normales en el intervalo [-3, +3] con igual varianza ( σ_θ² = 1 )y distinta media (caso 1: μ_θ = 0 y caso 2: μ_θ = -1). Esto proporcionó dos situaciones: no impacto donde las medias de ambos grupos (F y R) no difieren, e impacto donde la media del grupo focal fue de -1.

Para el conjunto de 75 items que forman el test bajo estudio se generaron aleatoriamente valores de dificultad y de discriminación. Los valores de discriminación se simularon para que adoptaran una distribución uniforme entre los límites [0.3, 2] y los de dificultad a partir de una distribución normal N(0,1) cuyos límites varían entre [-2.3, 2.3].

Para cada uno de los tamaños muestrales y situaciones (no impacto e impacto) se establecieron 9 condiciones donde se manipuló la cantidad de items con FDI en el test, el tipo de FDI (uniforme, no uniforme y mixto) y la cantidad de FDI (definido como diferencia, d_R-F, entre los parámetros de dificultad y/o discriminación de los grupos a comparar). Las condiciones manipuladas fueron:

1) 20% de los items con FDI y d_R-F = 0.4
2) 20% de los items con FDI y d_R-F= 0.7
3) 20% de los items con FDI y d_R-F= 1.0
4) 33% de los items con FDI y d_R-F = 0.4
5) 33% de los items con FDI y d_R-F = 0.7
6) 33% de los items con FDI y d_R-F = 1.0
7) 40% de los items con FDI y d_R-F = 0.4
8) 40% de los items con FDI y d_R-F = 0.7
9) 40% de los items con FDI y d_R-F = 1.0.

En cada una de estas condiciones el tipo de FDI generado fue en el mismo sentido. En todas las condiciones el número de items con FDI uniforme, no uniforme y mixto fue el mismo.

Generación de las matrices de datos

Según lo expuesto en el apartado anterior y teniendo en cuenta los 3 tamaños muestrales, los 2 tipos de distribución de habilidad y las 9 condiciones se dispone de un total de 54 combinaciones posibles con respecto al grupo focal. A cada una de estas condiciones corresponde una matriz de datos (sujetos x items). Esta matriz fue generada con el programa SIMULA v. 2 (Hidalgo y López, 1995) bajo el modelo logístico de 2-p.

Con la finalidad de encontrar resultados estables en cada una de las 54 combinaciones posibles, se obtuvieron 10 réplicas, sometiendo a estudio un total de 540 matrices. Para establecer la comparación correspondiente entre grupo de referencia y grupo focal fueron generadas 10 réplicas más por cada tamaño muestral a partir de la distribución normal N (0,1) de habilidad y de los valores iniciales de los parámetros de los items.

Detección del FDI

En el análisis de RL el FDI se evaluó en cada ítem mediante el modulo complementario LOGIT del paquete SYSTAT (Steinberg y Phillips, 1991). Las variables independientes definidas fueron: la puntuación observada del sujeto en el test tratada como un predictor continuo y la pertenencia a grupo. La variable dependiente fue la respuesta al ítem de naturaleza dicotómica.

Tanto en la aplicación del estadístico de Lord como de las medidas de área de Raju se estimaron, primeramente, los parámetros de los items en los grupos focal y de referencia, separadamente. Las estimaciones fueron realizadas con el programa BILOG versión 3.04 (Mislevy y Bock, 1990) utilizando las opciones por defecto del mismo. A continuación los parámetros estimados en ambos grupos fueron igualados utilizando el programa EQUATE versión 2.0 (Baker, 1993) que implementa el procedimiento de curvas características desarrollado por Stocking y Lord (1983). Por último, se calculó LORD - χ ², Z (AES) y Z (AEA) con el programa IRTDIF (Kim y Cohen, 1992b) que permite obtener las medidas anteriores.

Resultados

A fin de evaluar la eficacia de los procedimientos empleados, se han tenido en cuenta tanto el porcentaje de items con FDI correctamente identificados (IC), como el porcentaje de items que sin presentar FDI han sido detectados como tales, es decir, el porcentaje de falsos positivos (FP) a través de las 10 réplicas analizadas. En las tablas 1 a la 8 se presentan los resultados obtenidos en cada una de las condiciones manipuladas y estadísticos de FDI calculados. Estos aparecen en tres niveles de significación: 5%, 1% y 0.1% y resumidos en función del tipo de FDI generado: uniforme, no uniforme y mixto.

Situación de no impacto

Regresión Logística. Se puede observar que conforme aumenta la cantidad de FDI generado también aumenta el número de IC independientemente del tipo de FDI, del porcentaje de items con FDI y del tamaño muestral de los grupos focal y de referencia (ver tablas 1 a la 4). Con relación al tipo de FDI generado, el procedimiento de RL mostró, en todas las condiciones, mayor potencia en la detección de FDI no uniforme (diferencias sólo en el parámetro de discriminación) y mixto (diferencias en el parámetro de dificultad y discriminación). La tasa de IC más baja apareció en el caso en que el FDI manipulado era uniforme, aunque ésta se incrementó con el aumento del tamaño muestral y la cantidad de FDI. En las condiciones de mayor tamaño muestral y mayor cantidad de FDI las tasas de IC se situaron en valores similares para ambos tipos de FDI no uniforme, aunque los resultados globales indican que el análisis de RL tiene mayor potencia para detectar FDI no uniforme sobre FDI uniforme o mixto.

En cuanto al tamaño muestral, se encontró que un aumento del mismo supone también un aumento tanto de la tasa de IC como de FP. El número de FP se mantuvo cerca de los niveles nominales en las condiciones menos extremas (N=250 y d_R-F= 0.4) y fueron algo más elevados cuando los tamaños muestrales fueron altos (N=500 y N=1000), la cantidad de FDI fue mayor (0.7 y 1) y el porcentaje de items con FDI aumentó. Por el contrario, el aumento del número de items con FDI en el test no provocó una mejora en la tasa de IC, mostrándose en algunas situaciones la tendencia contraria.

En cualquier caso, tanto la tasa de IC como de FP se ven afectadas por el nivel de significación fijado. Si se considera el porcentaje de IC se observa que, en todas las condiciones de menor tamaño muestral (N=250 y N=500), sobre todo cuando la cantidad de FDI fue menor, éste disminuye conforme el nivel de significación es más restrictivo. Sin embargo, en las condiciones de tamaño muestral mayor ésta tendencia no se presenta tan marcada, de tal modo que los items correctamente identificados al 5% también lo son a niveles de significación más bajos (1% y 0.1%), excepto en el caso de FDI uniforme. El porcentaje de FP disminuye con el incremento del nivel de confianza, es decir, cuando los niveles de significación considerados fueron los más extremos, la tasa de FP fue también muy baja.

Medidas de Raju y de Lord. Los resultados encontrados, cuando se aplicaron las medidas de área de Raju y el estadístico de Lord, muestran que tanto el estadístico de Lord como Z(AEA) alcanzaron porcentajes de IC altos y similares. La medida de exacta de área con signo (Z(AES)) fue incapaz de detectar FDI no uniforme. Sin embargo, en cuanto a la identificación del FDI mixto y uniforme las tasas de IC para dicha medida con signo, concuerdan con las encontradas en los otros dos estadísticos utilizados (χ ² y Z(AEA)) (cf. tablas 1, 2 y 3). Al aumentar el número de items con FDI en el test mejoró la capacidad de Z(AES) para detectar correctamente items con FDI uniforme. Tal y como era de esperar a mayor cantidad de FDI generado mayor porcentaje de IC, tendencia que se mantiene a través de los diferentes tamaños muestrales y en las distintas pruebas estadísticas comparadas.

En cuanto al tamaño muestral, conforme éste aumenta se incrementa tanto la tasa de IC como de FP en los tres índices bajo estudio. El número de FP (cf. tabla 4) incrementó con el aumento del tamaño muestral, cantidad de FDI y porcentaje de items con FDI en el test. Solamente se mantienen cerca de los niveles nominales cuando la cantidad de FDI fue menor, el tamaño muestral fue de 250 ó de 500 sujetos y el porcentaje de items con FDI fue del 20%.

Cuando N=1000 y d_R-F = 1, el porcentaje de FP fue muy alto, más de la mitad de los items incorrectamente identificados, porcentaje que fue en aumento al incrementarse el número de items con FDI en el test. El estadístico de Lord mostró las tasas de FP más bajas, seguido de Z(AES) y de Z(AEA), sin embargo, con el incremento del porcentaje de items con FDI y en las condiciones más extremas de tamaño muestral y cantidad de FDI, el estadístico de Lord presentó tasas de FP ligeramente superiores a las obtenidas con los estadísticos de Raju.

La tasa de IC como de FP también estuvieron afectadas por el nivel de significación fijado. Si se considera el porcentaje de IC, se observa que en todas las condiciones de tamaño muestral pequeño y sobre todo cuando la cantidad de FDI fue menor, éste disminuye conforme el nivel de significación es más restrictivo. Sin embargo, en las condiciones de tamaño muestral mayor, ésta tendencia no se presenta tan marcada, de tal modo que los items correctamente identificados al 5%, también lo son a niveles de significación más bajos (1% y 0.1%). Por otro lado, con relación a la tasa de FP, ésta disminuye en todos los tamaños muestrales y condiciones con el incremento del nivel de confianza, es decir, cuando los niveles de significación considerados fueron los más bajos, la tasa de FP fue también muy baja. Aún así, en tamaños muestrales elevados y cuando la cantidad de FDI fue mayor, el número de FP fue considerable, incluso al nivel de significación más bajo.

Situación de Impacto

Regresión Logística. En las tablas 5 a la 8 aparecen los resultados encontrados en la situación de impacto cuando se aplicó análisis de RL. Se observa que, independientemente del tipo de FDI y del tamaño muestral de los grupos focal y de referencia, conforme aumenta la cantidad de FDI generado también aumenta el número de IC. Sin embargo, este incremento fue mayor de la condición 1 (d_R-F = 0.4) a la condición 2 (d_R-F = 0.7), que de ésta última a la condición 3 (d_R-F = 1).

Si se considera el tipo de FDI, tamaño muestral y nivel de significación se observa que el comportamiento del procedimiento de RL fue idéntico al obtenido en la situación de no impacto tanto con respecto al porcentaje de IC como al de FP.

Medidas de Raju y de Lord. Los resultados encontrados cuando se utilizaron las medidas de área y el estadístico de Lord (cf. tablas 5, 6 y 7) muestran que conforme aumenta la cantidad de FDI generado también aumenta el número de IC, tendencia que se mantiene en los tamaños muestrales de 250 y 500 sujetos. Cuando N=1000, la tasa de IC fue del 100% en χ² y Z(AEA) independientemente de la cantidad de FDI generado y del porcentaje de items con FDI. Por otro lado, Z(AES) alcanzó menor porcentaje de IC en relación a los otros dos estadísticos, y detectó peor el FDI no uniforme frente al FDI uniforme y mixto. Los estadísticos χ² y Z(AEA), siguiendo la pauta encontrada en la situación de no impacto, presentan porcentajes de IC similares en todas los tipos de FDI estudiados. No obstante, estos estadísticos identificaron menor porcentaje de items con FDI uniforme que con FDI no uniforme o mixto. Estos resultados fueron mejores con el aumento del tamaño muestral.

El número de FP se incrementó con el aumento en tamaño muestral y cantidad de FDI. La tasa de FP también estuvo afectada por el porcentaje de items con FDI, cuando éste aumentó también aumentaron el número de FP. Esto se produjo principalmente en las situaciones de menor tamaño muestral. En contraposición, el número de IC no varió con dicho aumento, excepto en la medida Z(AES) que mejoró la identificación de FDI no uniforme.

Las tasas de IC y FP estuvieron afectadas por el nivel de significación. En N=250 (independientemente de la cantidad de FDI generado) y N=500 (condición de d_R-F = 0.4) se observa que el porcentaje de IC disminuye conforme el nivel de significación se hace más restrictivo. En N=500 (condiciones de d_R-F = 0.7 y d_R-F = 1) y N=1000 (en todas las condiciones de cantidad de FDI) todos los items son identificados correctamente al 5% y también al 0.01%. En cuanto a la tasa de FP, ésta disminuye al considerar niveles de significación más restrictivos solamente en las condiciones de menor tamaño muestral.

Discusión

El porcentaje de identificaciones correctas, tal y como era de esperar, se dejo afectar por el tamaño muestral y la cantidad de FDI generado. Así, independientemente del estadístico de evaluación del FDI considerado, en las condiciones de mayor tamaño muestral y cantidad de FDI se produjeron mayor número de identificaciones correctas. Por el contrario, la presencia de diferencias entre grupos (impacto) no pareció afectar la precisión en la correcta identificación de items con FDI, algo a esperar dado que tanto RL como los estadísticos de la TRI son métodos que evalúan la presencia de FDI en función del nivel de habilidad. Por otro lado, la cantidad de items con FDI en el test tampoco resultó relevante en la detección correcta de items que funcionan diferencialmente.

Los estadísticos de la TRI frente al análisis de RL identificaron mejor el funcionamiento diferencial uniforme. Por contra, sólo en las condiciones menos extremas (menor porcentaje de items con FDI en el test, menor cantidad de FDI, menor tamaño muestral) los procedimientos derivados de la TRI obtienen porcentajes de IC más altos que RL en cuanto al FDI mixto. Por último, el FDI no uniforme es detectado igualmente bien por RL, Z(AEA) y χ² de Lord, siendo Z(AES) la que obtuvo los porcentajes de IC más bajos. El estadístico de Lord fue más efectivo en la identificación de FDI que Z(AES) y Z(AEA), resultados que concuerdan con los encontrados por Cohen y Kim (1993). Estos resultados llevan, en principio, a preferir el estadístico de Lord sobre el resto de procedimientos utilizados. Sin embargo, tanto χ² de Lord como Z(AEA) y Z(AES) controlan peor el porcentaje de FP, de tal modo que los valores encontrados fueron muy elevados y superiores a los encontrados cuando se utilizó RL. Esta circunstancia se dio principalmente en las condiciones de mayor cantidad de FDI, mayor tamaño muestral, mayor porcentaje de items con FDI y presencia de impacto entre grupos. En el caso de los estadísticos de la TRI, la presencia en el test de un alto porcentaje de items con FDI, las diferencias entre grupos y entre parámetros, pueden estar afectando seriamente al cálculo de las constantes de igualación. En este sentido, el cálculo de las mismas puede ser incorrecto y enmascarar la identificación correcta de FDI al mismo tiempo que identificaría un gran número de falsos positivos. Bajo estas situaciones es mejor utilizar un procedimiento iterativo de igualación (Candell y Drasgow, 1988; Kim y Cohen, 1992a; Lautenschlager, Flaherty y Park, 1994; Lautenschlager y Park, 1988; Miller y Oshima, 1992; Park y Lautenschlager, 1990) dado que proporciona resultados más fiables y decrementa el número de FP (Kim y Cohen, 1992a). En este punto, resultaría interesante comparar los efectos que se producirían al utilizar un procedimiento iterativo de purificación de la habilidad tanto para RL como los estadísticos de Lord y de Raju.

De los resultados obtenidos en este estudio se deduce también que, cuando se empleen las medidas de área de Raju y el estadístico de Lord, se debe trabajar con niveles de significación del 1% ó del 0.1%, dado que el porcentaje de FP se reduce sin disminución del porcentaje de IC.

En resumen, resulta más aconsejable, a la vista de los resultados aportados en este trabajo, el estadístico de Lord sobre el resto de procedimientos estudiados. Sin embargo, debido al escaso control que éste ejerce sobre la tasa de FP se recomienda emplear este estadístico junto a otra/s medidas de evaluación del FDI. Cohen y Kim (1993) sugieren que conjuntamente al estadístico de Lord se calculen las medidas exactas de área de Raju, la utilización de ambos procedimientos proporcionaría información complementaria en la evaluación del FDI. Los resultados de éste estudio apuntan a que el análisis de RL también puede utilizarse junto al estadístico de Lord. El análisis de RL fue precisamente el procedimiento que en las condiciones más extremas mostró el menor porcentaje de FP, si bien presentó el peor porcentaje de IC en lo que se refirió a la identificación de FDI uniforme.

Agradecimientos

Los autores agradecen al editor y a un revisor anónimo sus valiosos comentarios sobre la primera versión de este manuscrito.

Baker, F.B. (1993). EQUATE 2.0: A computer program for the characteristic curve method of IRT equating. [Computer program] Madison WI: University of Wisconsin. Laboratory of Experimental Design.

Candell, G.L. y Drasgow, F. (1988). An iterative procedure for linking metrics and assesing item bias in item response theory. Applied Psychological Measurement, 12, 253-260.

Clauser, B., Mazor, K.M. y Hambleton, R.K. (1993). The effects of purification of the matching criterion on the identification of DIF using the Mantel-Haenszel procedure. Applied Measurement in Education, 6, 269-279.

Cohen, A.S. y Kim, S.H. (1993). A comparison of Lord’s χ² and Raju’s area measures in detection of DIF. Applied Psychological Measurement, 17, 39-52.

Cohen, A.S., Kim, S.H. y Baker, E. (1993). Detection of Differential Item Functioning in the Graded Response Model. Applied Psychological Measurement, 17, 335-350.

Fidalgo, A.M. (1996). Funcionamiento diferencial de los items. Procedimiento Mantel-Haenszel y modelos loglineales. Tesis doctoral no publicada. Universidad de Oviedo.

Hambleton, R.K. y Rogers, H.J. (1989). Detecting Potentially Biased Test Items: Comparison of IRT Area and Mantel-Haenszel Methods. Applied Measurement in Education, 2, 313-334.

Hidalgo, M.D. (1995). Evaluación del funcionamiento diferencial del ítem en items dicotómicos y politómicos: un estudio comparativo. Tesis doctoral no publicada. Murcia, Universidad de Murcia.

Hidalgo, M.D. y López Pina, J.A. (1995). SIMULA 2.0: Un programa para la simulación de vectores de respuesta al ítem. Demostración de software presentada al IV Symposium de Metodología de las Ciencias del Comportamiento, La Manga, Murcia.

Holland, P.W. y Thayer, D.T. (1988). Differential item performance and Mantel-Haenszel procedure. En H. Wainer y H.I. Braun (Eds) Test Validity. Hillsdale, N.J.: Erlbaum.

Hosmer, D.W. y Lemeshow, S. (1989). Applied Logistic Regression. New York, NY: Wiley.

Kim, S.H. y Cohen, A.S. (1991). A comparison of two area measures for detecting differential item functioning. Applied Psychological Measurement, 15, 269-278.

Kim, S.H. y Cohen, A.S. (1992a). Effects of linking methods on detection of DIF. Journal of Educational Measurement, 29, 51-66.

Kim, S.H. y Cohen, A.S. (1992b). IRTDIF: A computer program for IRT differential item functioning analysis. Applied Psychological Measurement, 16, 158.

Lautenschlager, G.J., Flaherty, V.L. y Park, D. (1994). IRT differential item functioning: An examination of ability scale purifications. Educational and Psychological Measurement, 54, 21-31.

Lautenschlager, G.J. y Park, D. (1988). IRT item bias detection procedures: Issues of model misspecification, robustness and parameter linking.Applied Psychological Measurement, 12, 365-376.

Lord, F.M. (1980). Applications of item response theory to practical testing problems. Hillsdale, N.J.: Erlbaum.

Mellenbergh, G.J. (1982). Contingency table models for assesing item bias. Journal of Educational Statistics, 7, 105-118.

Miller, M.D. y Oshima, T.C. (1992). Effect of sample size, number of biased items and magnitude of bias on a two-stage item bias estimation method. Applied Psychological Measurement, 16, 381-388.

Millsap, R.E. y Everson, H.T. (1993). Methodology Review: Statistical Approaches for Assesing Measurement Bias. Applied Psychological Measurement, 17, 297-334.

Mislevy, R.J. y Bock, R.D. (1990). PC-BILOG: Item analysis and test scoring with binary logistic models. [Computer program]. Mooresville, IN: Scientific Software.

Navas, M.J. y Gómez, J. (1994). Comparison of several bias detection techniques. Paper presented at the 23rd. International Congress of Applied Psychology, Madrid.

Park, D.G. y Lautenschlager, G.J. (1990). Improving IRT item bias detection with iterative linking and ability scale purification. Applied Psychological Measurement, 14, 163-173.

Raju, N.S. (1988). The area between two item characteristic curves. Psychometrika, 53, 492-502.

Raju, N.S. (1990). Determining the significance of estimated signed and unsigned areas between two item response functions. Applied Psychological Measurement, 14, 197-207.

Rogers, H.J. y Swaminathan, H. (1993). A comparison of Logistic Regression and Mantel-Haenszel procedures for detecting differential item functioning. Applied Psychological Measurement, 17, 105-116.

Scheuneman, J. (1979). A new method for assessing bias in test items. Journal of Educational Measurement, 16, 143-152.

Steinberg, D. y Phillips, C. (1991). LOGIT: A supplementary module for SYSTAT. Evanston, IL: SYSTAT, Inc.

Stocking, M.L. y Lord, F.M. (1983). Developing a common metric in item response theory. Applied Psychological Measurement, 7, 201-210.

Swaminathan, H. y Rogers, H.J. (1990). Detecting differential item functioning using logistic regression procedures. Journal of Educational Measurement, 27, 361-370.

Thissen, D., Steinberg, L. y Wainer, H. (1988). Use of item response theory in the study of group differences in trace lines. En H. Wainer y H.I. Braun (Eds.) Test Validity. Hillsdale, N.J.: Erlbaum.

Thissen, D., Steinberg, L. y Wainer, H. (1993). Detection of Differential Item Functioning Using the Parameters of Item Response Models. En P.W. Holland y H. Wainer (Eds.) Differential Item Functioning (pp. 67-113). Hillsdale, NJ: LEA.

Aceptado el 8 de octubre de 1996